直線與圓錐曲線的位置關系

江西省南昌市鐵路第一中學 陳 輝

一、教學目標

1.知識與技能目標：能根據直線與圓的方程判斷其位置關系，體會用代數方法處理幾何問題的思想，能用數形結合的方法處理直線與圓的有關問題。

2.過程與方法目標：讓學生在解決數學問題的過程中，體會到數形結合、轉化、類比、歸納、猜想等數學思想方法。提高發現問題、分析問題、解決問題的能力。

3.情感、態度與價值觀目標：讓學生親身經歷知識生成的過程，體驗探索的樂趣，增強學習興趣；在“數”與“形”的對立與統一中，加強辯證唯物主義思想教育。

二、教學重點、難點

1.教學重點：（1）掌握直線與圓的位置關系的判定方法。

（2）運用數形結合和轉化的思想方法，處理直線與圓的有關問題。

2.數學難點：“數”與“形”之間的轉化技巧與方法。

三、學情分析及復習策略

對于解析幾何，雖然每年花費大量的時間和精力進行復習訓練，但解析幾何的得分率都不高，原因是考生在學習解析幾何時有畏懼心理,認為解析幾何很難,考試時不敢做,放棄解析幾何大題。

針對我們學生的實際情況，我在復習時主要讓學生熟悉一些常見題目的解答模型，為學生做題指引思路方向，克服恐懼心理，再逐步提高難度、靈活性和綜合性，從而提高得分率。

四、教學過程設計

（一）回歸教材，整合要點

復習直線與圓錐曲線的位置關系、弦長公式、點差法、直線設法討論。

（二）課前練習，夯實雙基

若過原點的直線l與雙曲線有兩個不同交點，則直線l的斜率的取值范圍是( )

（三）例題講解，授人以漁

題型一：弦長問題

例1 在直角坐標系xOy中，直線l：y=t（t≠0）交y軸于點M，交拋物線C：y2=2px（p＞0）于點P，M關于點P的對稱點為N，連接ON并延長交C于點H，

又N為M關于點P的對稱點，故

ON的方程為代入y2=2px整理得px2-2t2x=0，解得x1=0

設計意圖：通過本題讓學生充分體會弦長與坐標的相互轉化關系。

題型二：對稱問題

例2 試確定m的取值范圍，使得橢圓上有不同兩點關于直線l：y=4x+m對稱。

解：設AB中點坐標(x0，y0)，由點差法得即y0=3x0，

又(x0，y0)∈l，y0=4x0+m，∴AB中點坐標（-m，-3m）。

∵中點（-m，-3m）在橢圓內部，

設計意圖： 通過本題讓學生充分體會如何將對稱關系轉化為代數關系。

題型三：面積問題

例3 如圖所示，拋物線的頂點為O，點A(5,0)，傾斜角的直線l與線段OA相交(不經過點O或點A)且交拋物線于M、N兩點，求△AMN的面積最大時直線l的方程，并求△AMN的最大面積。

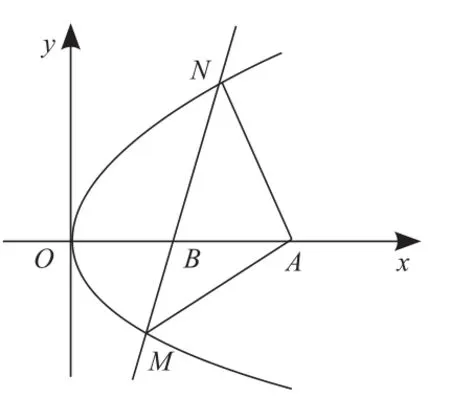
解：設l：y=x+m,m

設M(x1，y1),N(x2，y2), 則x1+x2=4-2m，x1x2=m2。

∴△AMN的面積

從而

故直線l：y=x-1，△AMN的最大面積為

總結：將面積用底（弦長）和高（點到直線的距離）表示。

題型四：向量問題

解：設A(x1，y1),B(x2，y2)，M(0,2)。由

易知AB斜率存在，設AB：y=kx+2。

∴AB：

總結：將向量用坐標表示，結合x1+x2，x1x2消去x1、x2。

（四）課堂小結，提煉知識

（五）教學反思，查缺補漏

在教學中要重視基礎，回歸課本，先做比較基礎的、典型的題型，然后逐漸提高難度，加入一些思維量比較大的題目，提高學生的分析能力及相關性質的靈活運用能力、計算整理能力，突破難點，克服恐懼心理。

（六）課后訓練，鞏固提高