利用基本圖形巧解中考題

安徽省阜陽市第十一中學 劉 穎

數學中，幾何圖形大都由基本圖形復合而成，因此，熟悉常見的基本圖形及探究圖形間的聯系，有助于快速準確地從復雜的圖形中分解出自己所熟知的基本題型和基本圖形。對這些基本圖形的條件和結論進行探索，對學生解決相似及中考壓軸問題都是十分有用的。

一、常見的幾種基本圖形

（一）三角形中的相似

1．平行線型

圖1-1

圖1-2

2．相交線型

圖2-1

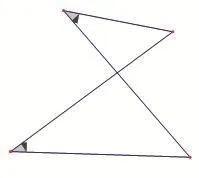
圖2-2

3．母子型

圖3

4．三角相等型

圖4-1

圖4-2

（二）圖形變換之中的旋轉

1．旋轉不變性

如圖5，由△OAB繞O點逆時針旋轉90度后得到△OA'B'。易知△OAB≌△OA'B，連接AA',BB'。

則有：①△OAA'和△OBB'是等腰三角形且∠AOA'=∠BOB'；②∠BPB'=∠BOB'。

圖5

2．旋轉相似性

如圖6，△OAB∽△OA'B' ,則有：①△OAA'∽△OBB'；

②∠BPB'=∠BOB'。

圖6

二、基本圖形在安徽中考題中的應用

例1 如圖7，已知△ABC、△DEF均為正三角形，D、E分別在AB、BC上。請找出一個與△DBE相似的三角形并證明。

分析：由題中條件可知，此題是三角相等型和相交線型基本圖形的應用，首先分解原題圖形為基本圖形：

圖7

圖 7-1

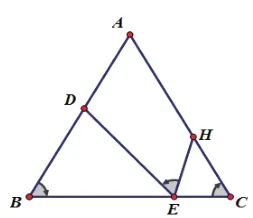
圖 7-2

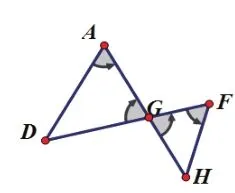
圖 7-3

圖 7-4

由圖7-1可知△DBE∽△GAD，由圖7-2可知△DBE∽△ECH，由圖7-3可知△GAD∽△GFH，綜上還可得△DBE∽△GFH。

例2 （歷年安徽中考）如圖8，四邊形ABCD和四邊形ACED都是平行四邊形，點R為DE的中點，BR分別交AC、CD于點P、Q。

（1）請寫出圖中各對相似三角形（相似比為1除外）；

圖8

（2）求BP∶PQ∶QR。

分析：由題中條件可知，此題是平行線型基本圖形的應用，首先分解原題圖形為基本圖形：

圖 8-1

圖 8-2

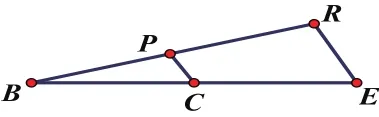
圖 8-3

（1）由圖8-1可知△PAB∽△RDQ，由圖8-2可知△PCQ∽△RDQ，由圖8-3可知△BCP∽△BER，又由△PAB∽△RDQ和△PCQ∽△RDQ知△PCQ∽△PAB。

（2）因為四邊形ABCD和四邊形ACED都是平行四邊形，所以BC=AD=CE，結合圖8-3可知PB=PR圖8-2可知再結合DR=RE和所以QR=2PQ，又因為BP=PR=PQ+QR=3PQ，所以BP∶PQ∶QR=3∶1∶2。

通過以上例題，我們可以感受到復雜圖形可以分解為簡單的基本圖形，從而使解題依據更加明確，解題思路更加明晰，這樣使解決問題的難度得以降低，達到“化繁為簡”和快速解決問題的目的。