高中數學立體幾何的學習體會

湖南省婁底市第三中學 陳 萌

高中數學學科中的立體幾何主要研究空間形狀、大小、位置關系等內容，它是數學學科學習的核心內容。但在具體學習立體幾何數學知識時，我認為應摒棄傳統死記硬背的學習方法，以實踐動手作圖等解題方式，解決一系列立體幾何問題，達到最佳的知識求解效果，并學會將立體幾何知識應用到日常生活問題解決中。以下是關于我的一些數學知識學習體會，望其能為其他高三學生學習提供一些有力參考。

一、歸納相關概念

在學習高中數學立體幾何知識時，將涉及很多公理和定理概念的記憶。為了提高相關概念記憶效率，應導入思維導圖法，歸納概念方面的知識。如圖1所示：

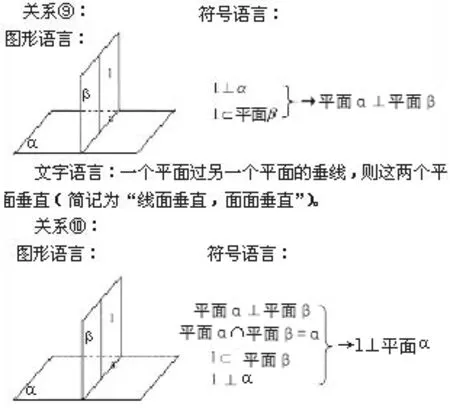
圖1 （思維導圖）

我在立體幾何中記憶直線與平面、平面與平面的平行或垂直關系時，為了更好地內化所學內容，以圖形語言和符號語言記憶方式制作了一個思維導圖，通過這一思維導圖的制作，讓我更為透徹地理解了所學內容。

思維導圖是幫助我們記憶復雜知識點的有效辦法，應強調對它的運用，達到最佳的知識學習效果。

二、實踐動手作圖

我認為高中數學立體幾何知識的學習也需要我們多多嘗試動手作圖。

例1 ABCD -A1B1C1D1是一個正方體，在這個正方體中，P是AA1中點，C是這個正方體的底面中心，計算PO與C1BD所成角度。

在解決這道立體幾何數學問題時，為了提高數學問題求解效率，得出正確答案，我依照題目中所給的條件，動手繪制了一個符合題意的立體幾何圖形，同時，在繪制圖形的基礎上，連接了立體幾何中的A1C和AC，如圖2所示。

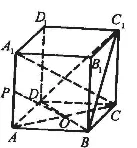
圖2 立體幾何）

通過這一立體幾何圖形的繪制，我很快證明出了PO與C1BD所成角度是90°。即從所繪制的立體幾何圖示可看出，PO∥A1C，AC又是A1C在底面ABCD中的射影，又因BD⊥AC，所以，BD⊥A1C，同理，A1C⊥B1C，故A1C⊥C1BD，PO與C1BD垂直。

立體幾何圖示的直觀性較強，我認為，在求解立體幾何問題時，若可實踐動手作圖，將在一定程度上簡化問題求解過程，讓問題變得更加簡單，快速得出問題答案。我提議，在學習高中數學立體幾何時，應突破死記硬背的學習方式，靈活使用立體幾何圖形，通過對圖形的觀察，理清問題解決思路，達到最佳的問題解決效果。

三、總結錯誤題型

我認為，在學習高中數學立體幾何知識時，可以建立一個錯題本，總結錯誤題型，有利于幫助我們深刻記憶錯誤原因，對問題進行改正。

例如，我在學習立體幾何知識時，根據錯題類型，建立了關于知覺想象錯誤、特殊代替一般證明錯誤、理解定義錯誤、構造圖形錯誤、建模錯誤方面的錯題本。其中，在歸納理解定義錯誤時，收錄了如下一道經典題目：

已知ABCD是一個空間四邊形，如若AB與CD相等，同時，二者的角呈60°，假設M、N分別是BC、AD的中點，求AB與MN之間所成角度。

錯誤原因：我在題目求解時，對異面直線所成角定義的理解不夠透徹，在具體問題解決中，先是作了一條直線MP，保持MP∥AB，與AC相交于P點，如圖3，但最終遺漏了PM與PN成60°角時，∠MPN=120°條件的分析。

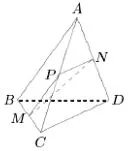
圖3

通過錯題的總結，實現了我對問題的深刻反思，避免了類似錯誤的再次出現。

綜合我以往的高中數學立體幾何學習體會，我認為在學習高中數學立體幾何知識時，應突破傳統死記硬背的學習方式。這種學習方式不利于我們數學思維的養成，應嘗試在歸納一些數學概念的基礎上，參與更多的實踐動手活動，并嘗試總結一些錯誤題型，通過錯誤總結，不斷改正錯誤問題，避免錯誤問題的再次發生，達到高效求解立體幾何問題的效果，不再進入數學知識的學習誤區，養成良好的學習習慣。

[1]徐章韜，劉鄭，劉觀海等．基于立體幾何智能教育平臺的TCK：功用、存在方式及教育意義[J]．電化教育研究，2012，33（12）：104-109．

[2]謝旭清．新課改下高中數學立體幾何有效教學的策略[J]．學周刊，2014，40（33）：82．

[3]鄧天發．高中立體幾何教學如何培養學生空間想象能力[J]．學周刊，2016，42（36）：177-178．