一種基于遺傳算法和BP神經網絡的對流層延遲改正模型

陳 陽,胡伍生

(東南大學 交通學院，江蘇 南京 210096)

近三十年來，隨著電子、通信和航天等現代科技手段的飛速發展，與電磁波傳播密切相關的大氣層，尤其對流層已經成為影響人類生產和生活的重要因素之一。從地面向上約40 km范圍內的大氣底層稱為對流層。衛星信號經過對流層時，受大氣折射影響產生時延和路徑彎曲導致的信號延遲，即為對流層延遲。對流層延遲是影響GNSS(Global Navigation Satellite System，GNSS)導航定位的重要誤差源，其延遲量在天頂方向大約為2 m，在接近地面方向在20 m左右[1]。因此，進行對流層延遲的研究具有重大意義。

國際上獲取對流層天頂延遲(Zenith Tropospheric Delay，ZTD)的方法有很多，主要有：無線電探空儀法(Radiosonde)、水汽輻射計法(Water Vapor Radiometer)、GNSS提取法、甚長基線干涉測量技術(Very Long Baseline Interferometry，VLBI)和模型改正法等[2]。由于模型改正法的普適性和廉價性，在對流層延遲方面得到深入研究和廣泛應用。ZTD模型按照模型是否需要實測氣象參數，分為實測氣象參數ZTD模型和經驗ZTD模型。第一類實測氣象參數ZTD模型主要包括Hopfield模型、Saastamoinen模型及Black模型等。1969年，Hopfield對全球18個高空氣象探測臺站兩年的資料進行細致的分析，初步建立了大氣模型[3]。1973年，Saastamoinen基于美國標準大氣模型計算得到天頂延遲，建立Saastamoinen模型[4]。1978年，H.D.Black在 Hopfield模型基礎上加入路徑彎曲改正之后，推導出Black模型[5]。實測氣象參數ZTD模型需要利用溫度、壓力和水汽壓等氣象參數解算ZTD，而在大部分情況下用戶無法獲取實測的氣象數據，限制此類模型的實用性。第二類經驗ZTD模型在計算ZTD時不需要輸入氣象參數，主要包括UNB系列模型、EGNOS模型、IGGtrop模型、GZTD模型、GPT系列模型。2004年RodrigoLeandro等人在大量全球氣象資料的基礎上建立UNB模型，該模型綜合考慮溫度、壓力和水汽壓等氣象參數在空間上的變化，通過緯度和年積日的表格形式來表示氣壓、溫度、相對濕度等氣象參數[6]。UNB3模型則是將UNB模型表格中的相對濕度換成了水汽壓。在全球范圍內，UNB3模型的改正精度與實測氣象參數的Hopfield模型相當。EGNOS模型在UNB3模型的基礎上進行改進，考慮溫度、氣壓、水汽壓、溫度梯度、水汽梯度這5個氣象參數。EGNOS模型系數依賴于測站的經緯度和時間，而且精度與Saastamoinen模型相當，已用于美國、歐洲等地區的增強導航系統中[7]。2012年李薇等人利用NCEP大氣資料和IGS中心提供的ZTD時間序列等產品，考慮到不同測站經緯度的差異建立全球對流層天頂延遲模型IGGtrop[8-9]，該模型在全球的改正精度在5cm左右，其改正效果要優于EGNOS模型和UNB系列模型。2013年，姚宜斌等學者利用2002—2009年全球ZTD格網時間序列提出一種基于球諧函數的GZTD全球對流層天頂延遲改正模型，其模型精度可達到4～5 cm左右[10-13]。2013年Johannes B?hm等人利用3年的ERA-40數據采用9階9次球諧函數得到GPT模型，提供分辨率為15°×15°全球格網數據[14]。2014年，K.Lagler等人在GPT的基礎上，建立了空間分辨率為5°×5°的GPT2模型[15]。2015年Johannes B?hm等人利用ECMWF提供的2001—2010年全球月平均的氣壓、氣溫、比濕的氣象資料建立了GPT2w模型，它以5°×5°或1°×1°的分辨率提供全球格網點上的氣壓、溫度、比濕等信息，其在全球范圍內的改正效果可達到3.5～4 cm左右[16]。

雖然UNB3、EGNOS等經驗模型在全球平均修正效果較好，但在某些特定區域，不能很好的進行延遲誤差修正。同時IGGtrop、GPT2w等模型的缺陷是需要大量的外部格網數據作為初始使用條件，如GPT2w模型需要約1632000個外部格網數據作為輸入，限制GNSS用戶使用的便捷性[17]。針對上述問題，建立無需大量初始數據的區域內高精度對流層延遲改正模型具有迫切的必要性和重要意義。

由于對流層的影響因素多，許多因素又帶有較大的隨機性，導致對流層延遲具有很多不規則的變化。BP神經網絡通過其學習、記憶和計算等功能，可從環境信息復雜、推理規則不明確的非線性空間系統中挖掘出其隱含的規律[18]。利用BP神經網絡技術可以對現有對流層延遲改正模型進行修正，進而實現對流層延遲變化的擬合。遺傳算法是一種概率搜索算法，它的基本思想是通過全面模擬自然選擇和遺傳機制，通過對種群個體的選擇、雜交和變異，形成一種具有“生成+檢驗”特征的搜索算法[19-20]。針對BP神經網絡學習過程中容易陷入局部最小值或過度擬合情況，利用遺傳算法的“自適應”和“自進化”原理，優化神經網絡的初始權值和閾值，改善神經網絡學習能力的可靠性和穩定性。

針對目前對流層研究領域設有把遺傳算法和BP神經網絡技術結合應用于建立預測模型這一現象，本文在EGNOS模型基礎上，利用遺傳算法和BP神經網絡技術，消除EGNOS模型在北美洲區域的誤差，建立一種無需大量初始數據的高精度區域融合模型(GA-BPEGNOS模型)。

1 EGNOS模型基本原理

EGNOS模型是在UNB3模型基礎上建立的，該模型包括氣壓、溫度、水汽壓、溫度梯度和水汽梯度這5個氣象參數，并且認為它們在平均海平面上的變化與年積日和測站的地理位置有關。研究發現，這5個氣象參數的數值由兩部分組成，即年平均值Avg和年變化量Amp。這兩個數值隨著緯度的變化而變化。

根據式(1)和式(2)可計算出相應緯度五個氣象參數的年平均值和年變化值。

Avgφ=

(1)

Ampφ=

(2)

式中：LAT代表緯度符號；i為對應的緯度數值。

利用這5個氣象參數的年平均值和年變化值，根據式(3)即可計算出對應年積日的5個氣象參數。

Xφ,doy=Avgφ+Ampφ×

(3)

首先利用測站的緯度和年積日計算出平均海平面處的對流層延遲，平均海平面處的天頂靜力延遲(Zenith Hydrostatic Delay，ZHD)和天頂濕延遲(Zenith Wet Delay，ZWD)分別為

(4)

(5)

其中，k1=77.064 K/mbar；gm=9.784 m/s2；R=287.054 J/kg·K；P0為平均海平面處的氣壓；k2=38 200 K2/mbar；e0為平均海平面處的水汽分壓。

然后利用測站的高程計算測站處的對流層延遲，接收機處對流層干延遲和濕延遲分別為

(6)

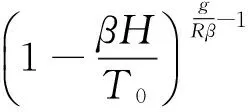
(7)

式中：g=9.806 65 m/s2；H為接收機處的高程；T為平均海平面的溫度。

EGNOS模型計算部分測站的ZHD、ZWD和ZTD如表1所示。

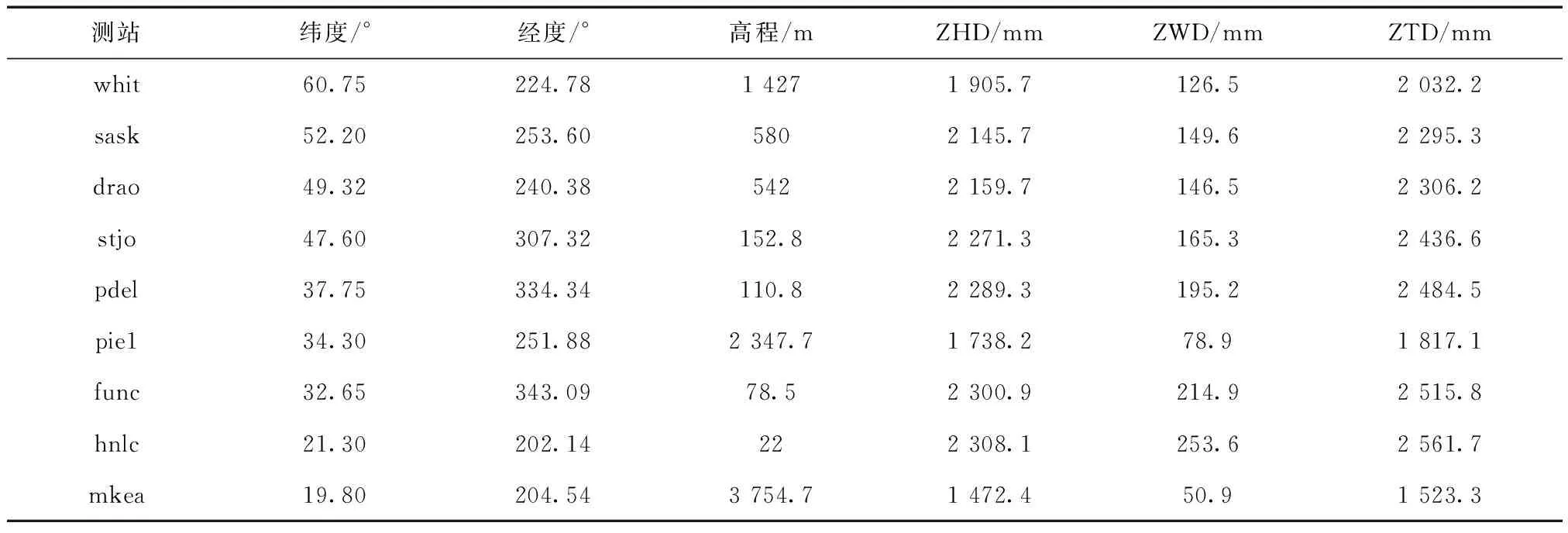
表1 EGNOS模型計算部分測站的對流層延遲

2 遺傳算法和BP神經網絡基本原理

2.1 遺傳算法基本原理

遺傳算法(Genetic Algorithms)是1962年美國Michigan大學Holland教授提出的模擬自然界遺傳機制和生物進化論的一種并行隨機搜索最優化方法。它把自然界“優勝劣汰，適者生存”的生物進化原理運用到優化參數形成的編碼串聯群體中，按照所選擇的適應度函數，通過遺傳中選擇、交叉和變異過程對個體進行篩選，保留適應度值好的個體，淘汰適應度差的個體。新的群體既繼承了上一代的信息，又優于上一代。這樣反復循環，直至滿足條件。

2.2 BP神經網絡基本原理

BP(Back Propagation)神經網絡又稱為誤差反向傳播神經網絡，是一種多層前向型神經網絡。在BP神經網絡中，信號向前傳播，誤差反向傳播。所謂反向傳播是指誤差從最后的輸出層依次向之前各層逐漸進行調整。神經網絡不僅具有學習、記憶和計算等功能，同時其強大的非線性擬合能力可以處理一些復雜的非線性問題。由于對流層的影響因素很多，許多因素又帶有較大的隨機性，可利用神經網絡從環境信息復雜、推理規則不明確的非線性空間系統中挖掘出其隱含規律，從而實現對流層延遲變化的擬合。

針對神經網絡有時會陷入局部最小值或過度擬合情況，在用神經網絡進行模型擬合訓練前，利用遺傳算法的自然選擇和遺傳機制，對個體進行選擇、交叉和變異處理，逐步優化神經網絡的權值和閾值。這樣不僅可以提高神經網絡的穩定性，還可以改善神經網絡的學習能力，得到高精度的對流層延遲預測模型。

3 融合模型(GA-BPEGNOS模型)的構建

EGNOS模型是根據全球平均氣象資料建立的改正模型，其緯度格網劃分比較稀疏，無法準確描述小區域范圍內的對流層延遲變化規律。針對上述特點，本文通過遺傳算法和BP神經網絡技術，在EGNOS模型基礎上建立一種高精度區域融合模型，構建融合模型的網絡結構圖如圖1所示。

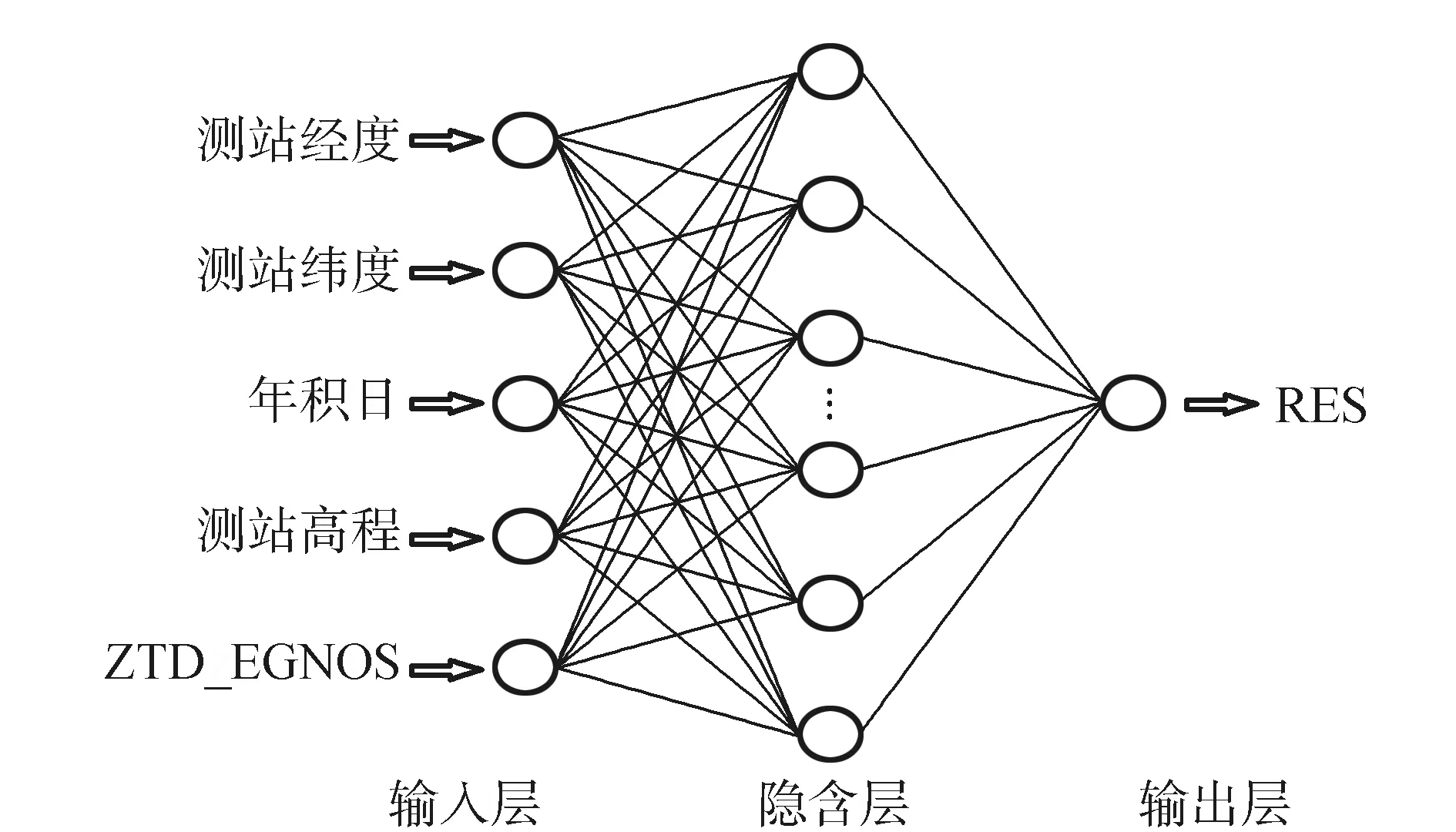
圖1 融合模型的網絡結構

融合模型(GA-BPEGNOS模型)構建的具體過程如下：

1)融合模型網絡拓撲結構：構建一個5×P×1的BP神經網絡模型，表示測站處對流層延遲殘差RES與測站經度、測站緯度、測站高程、年積日和EGNOS模型計算的測站對流層延遲的非線性關系；

2)遺傳算法部分：首先進行數據輸入和數據預處理，然后對初始值進行編碼，根據BP神經網絡的適應度值，通過遺傳算法中的選擇操作、交叉操作和變異操作不斷優化神經網絡的權值和閾值，直至滿足條件結束；

3)BP神經網絡算法：利用IGS中心提供的高精度對流層延遲產品和遺傳算法得到的優化權值和閾值，對建立的BP神經網絡結構進行訓練。利用測站經度、測站緯度、測站高程、年積日和EGNOS模型計算的測站對流層延遲計算出測站處對流層延遲殘差RES(RES=ZTD_IGS-ZTD_EGNOS)，ZTD_IGS為IGS中心提供的高精度ZTD數據，ZTD_EGNOS為EGNOS模型計算的ZTD；

4)融合模型對流層延遲：根據BP神經網絡預測的對流層延遲殘差RES_BP和EGNOS 模型計算的測站對流層延遲ZTD_EGNOS，得到融合模型的對流層延遲ZTD_GA-BPEGNOS(ZTD_GA- BPEGNOS =RES_BP+ZTD_EGNOS)，ZTD_GA-BPEGNOS為融合模型的ZTD，RES_BP為BP神經網絡預測的對流層延遲殘差。

4 實驗結果與分析

為了驗證融合模型的精度，選取北美洲(西經[10°～160°],北緯[10°～80°]) 41個測站點，以IGS中心提供的2010—2014年ZTD產品作為真值進行驗證。

以20個均勻分布測站點2011—2012年共13 727個對流層延遲數據訓練神經網絡，建立基于遺傳算法和BP神經網絡技術的融合模型。以35個均勻分布測站(包括14個訓練測站和21個未知測站)2013—2014年共23 927個對流層延遲數據來檢驗融合模型預測精度。融合模型具有強大的預測功能，不僅時效性良好，可預測2013—2014年ZTD，同時也擴大空間預測范圍，35個檢驗測站中除了14個訓練測站外，還包括21個未知測站。訓練和檢驗測站分布如圖2所示，其中紅色點為訓練測站的位置，藍色星號為檢驗測站的位置。

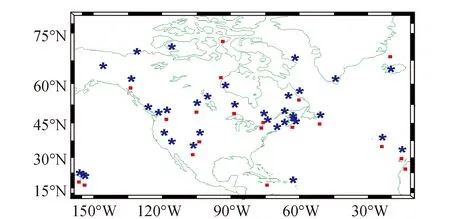
圖2 訓練測站和檢驗測站分布圖

以平均偏差(BIAS)和均方根誤差(RMSE)作為評價模型精度的標準，具體算式

(8)

(9)

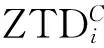
4.1 實驗結果

EGNOS模型和融合模型計算的平均偏差(BIAS)和均方根誤差(RMSE)如表2所示。

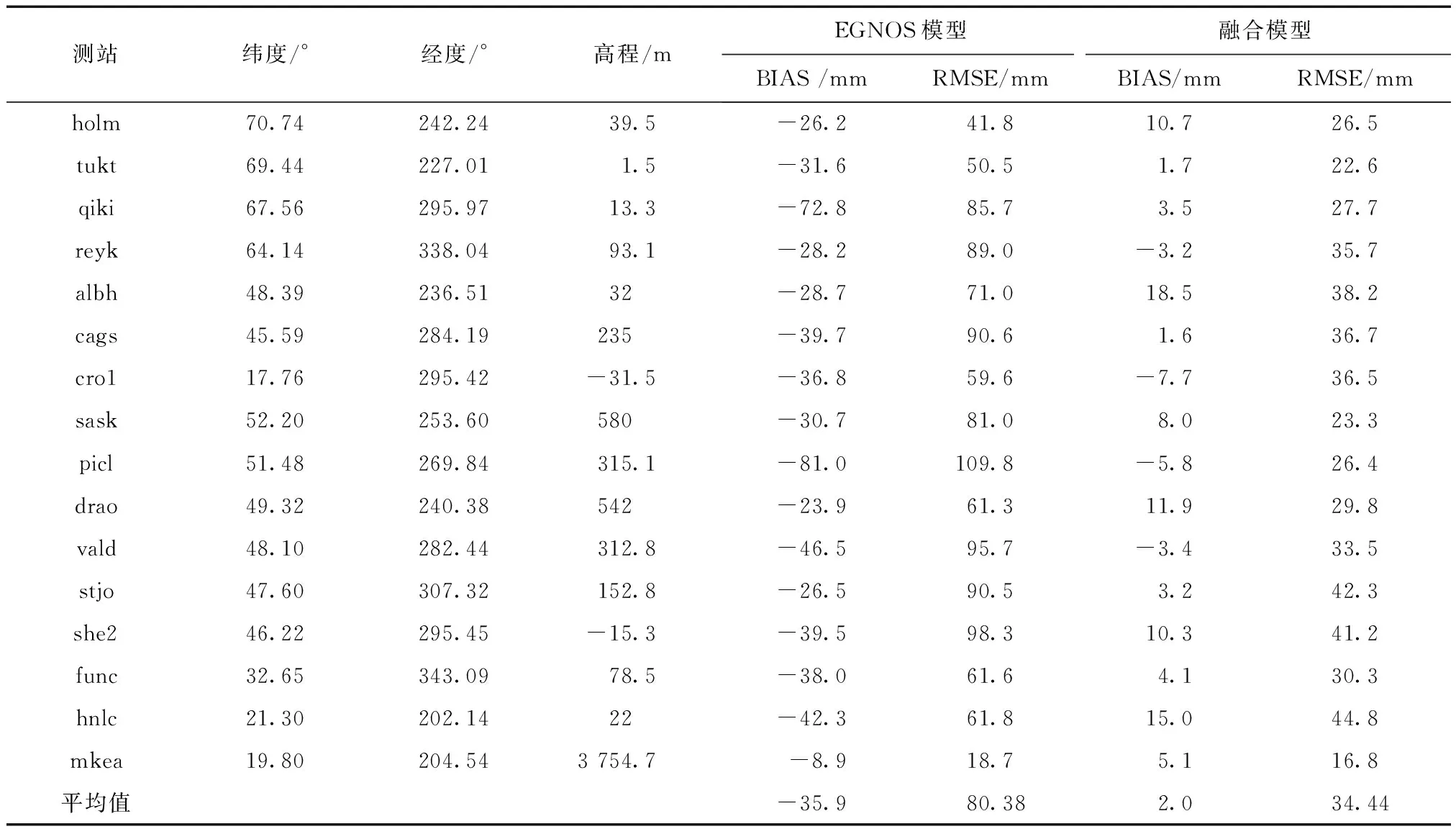
表2 部分檢驗測站的平均偏差和均方根誤差

4.2 精度分析

35個檢驗測站高程和ZTD均值如圖3所示。

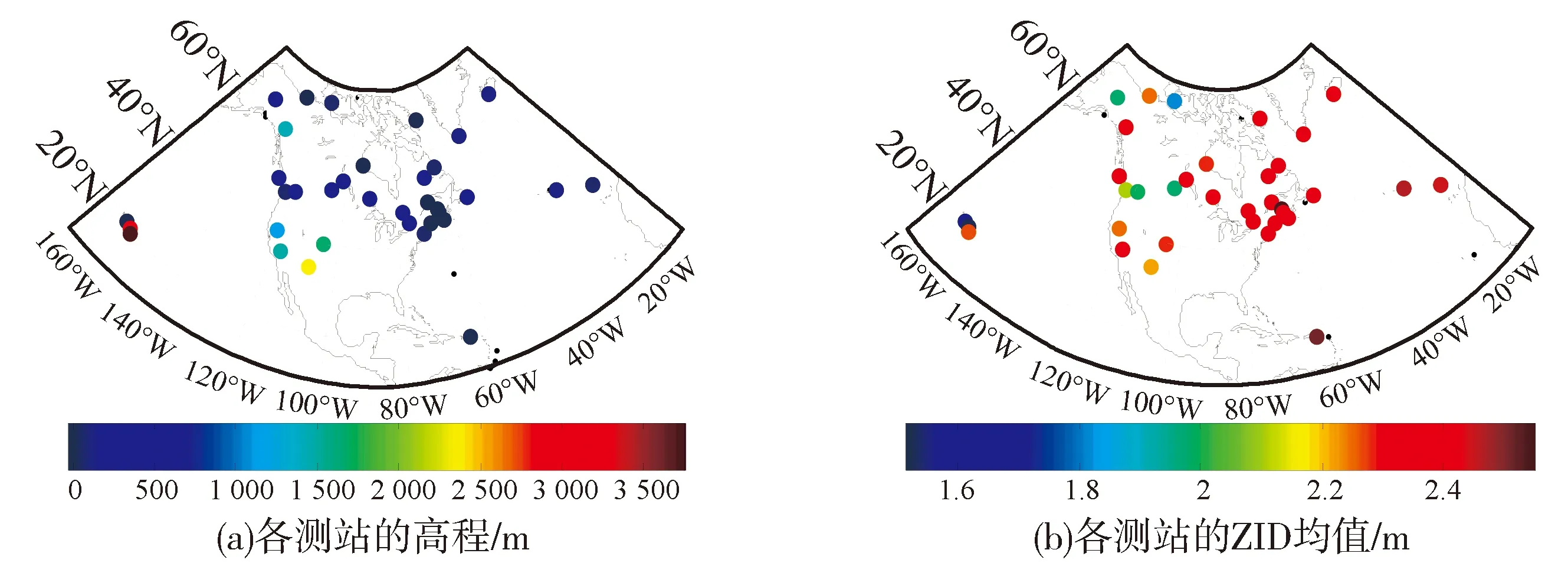
圖3 35個檢驗測站的高程和ZTD均值(2013～2014)

由圖3(a)可知，35個檢驗測站較為均勻的分布于北美洲，除了西經160°、北緯20°處的2個測站高程較大，其余測站的高程大致相同。從圖3(b)可以看出，相比其它測站，西經60°、北緯45°處的幾個測站ZTD均值較大，主要原因為該地區靠近海岸帶，水汽較活躍，ZWD較高。

EGNOS模型計算35個檢驗測站ZTD的BIAS和RMSE情況如圖4所示。

由圖4(a)可知，EGNOS模型求得大部分檢驗測站的BIAS為負值，說明EGNOS模型在計算北美洲ZTD時存在系統偏差，35個檢驗測站的平均BIAS為-3.6 cm。從圖4(b)檢驗測站RMSE的顏色分布可以發現，EGNOS模型的RMSE變化幅度很大，從最小值1.8cm變化到最大值11.8 cm。西經60°、北緯45°處的幾個測站處EGNOS模型RMSE普遍大于10 cm，再次證明該處水汽變化顯著，ZWD隨機性較強。35個檢驗測站2013—2014年的EGNOS模型平均RMSE為8.0 cm。

融合模型計算35個檢驗測站ZTD的BIAS和RMSE情況如圖5所示。

由圖5(a)發現融合模型的BIAS變化幅度在-2.5～1.5 cm之間，35個檢驗測站的平均BIAS為2 cm，可知融合模型計算該地區ZTD時，模型偏差小且比較穩定。圖5(b)看出融合模型的RMSE在1.6～4.7 cm之間變化，西經60°、北緯45°處的幾個測站處融合模型RMSE普遍大于4 cm。該處EGNOS模型和融合模型的RMSE都比較高，再次證明該處水汽變化顯著。35個檢驗測站整體的平均RMSE為3.4 cm。相比EGNOS模型，融合模型在計算北美地區的ZTD時具有較高精度。

35個檢驗測站的ZTD偏差和ZTD分布圖如圖6所示。

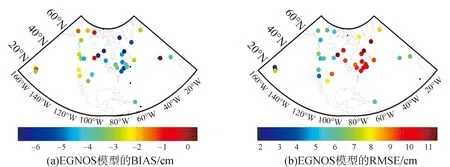
圖4 EGNOS模型計算ZTD的BIAS和RMSE(2013—2014)

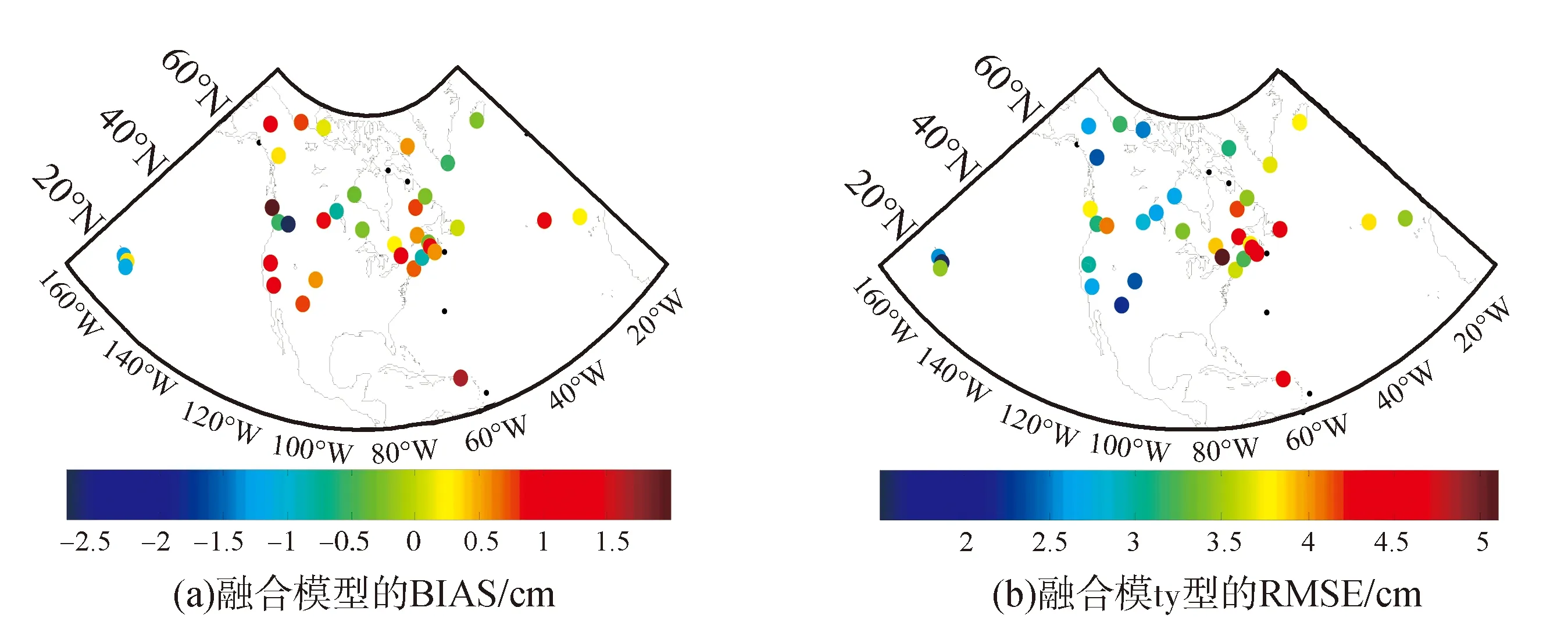
圖5 融合模型計算ZTD的BIAS和RMSE(2013—2014)

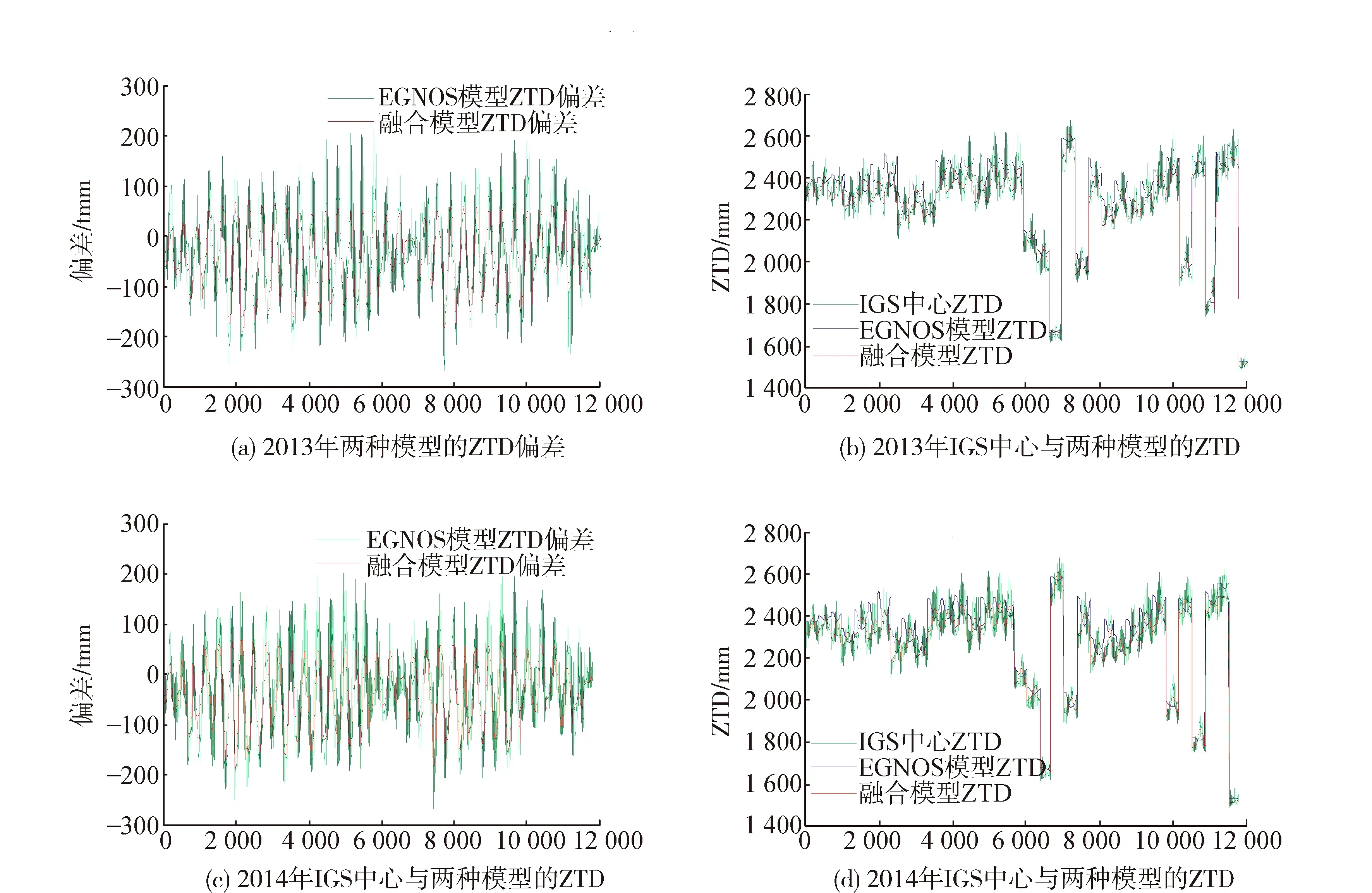
圖6 35個檢驗測站的ZTD偏差和ZTD分布圖(2013—2014)

由圖6中(a)、(c)可知2013年和2014年兩種模型的ZTD偏差情況十分接近，EGNOS模型偏差變化幅度大，范圍在470 mm左右。融合模型的偏差變化在260 mm左右。通過比較模型的偏差范圍可以發現，融合模型偏差變化幅度最小，說明其具有更好的穩定性。由圖6(b)、(d)可以得到相比藍色EGNOS模型ZTD的變化情況，紅色的融合模型ZTD走向更加趨近于綠色的IGS中心ZTD。相比EGNOS模型，融合模型具有更高精度。

35個檢驗測站2013—2014年EGNOS模型和融合模型的ZTD偏差如表3所示。

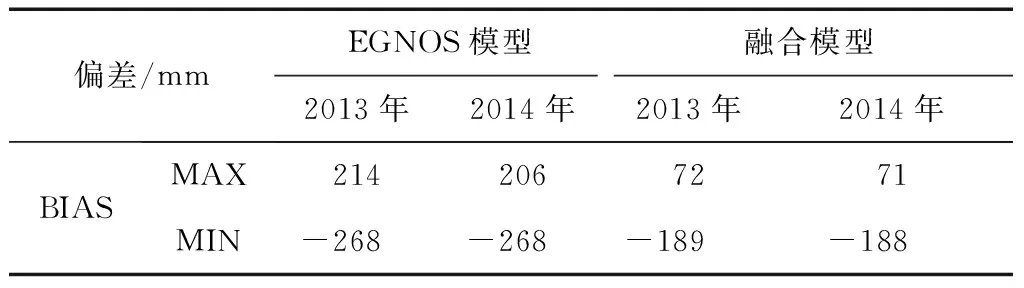
表3 檢驗測站的ZTD偏差范圍

比較分析模型偏差，發現EGNOS模型ZTD偏差變化從-268～214 mm，融合模型ZTD偏差范圍為-189～72 mm。融合模型的ZTD偏差范圍小于EGNOS模型的ZTD偏差范圍，證明EGNOS模型不穩定。相比EGNOS模型，融合模型的穩定性得到明顯改善。

5 結 論

經上述研究，本文得出如下結論：

1)與EGNOS模型相比，基于遺傳算法和BP神經網絡技術的融合模型精度有明顯提高，提高比例約57%。

2)與IGGtrop、GPT等經驗模型相比，融合模型不僅具有高精度，同時無需大量初始格網數據輸入的優勢，方便用戶的廣泛使用。

3)本文未進行融合模型的應用研究。下一步即將把融合模型應用于精密單點定位中，分析融合模型使用前后對收斂速度和高程方向精度的影響。

[1] LI W, YUAN Y B, OU J K, et al. A new global zenith tropospheric delay model IGGtrop for GNSS applications [J]. Science Bulletin, 2012, 57(17):2132-2139.

[2] 張雙成, 張鵬飛, 范朋飛. GPS對流層改正模型的最新進展及對比分析[J]. 大地測量與地球動力學, 2012, 32(2):91-95.

[3] HOPFIELD H S. Two‐quartic tropospheric refractivity profile for correcting satellite data [J]. Journal of Geophysical Research Atmospheres, 1969, 74(18):4487-4499.

[4] SAASTAMOINEN J. Contributions to the theory of atmospheric refraction [J]. Bulletin Géodésique (1946-1975), 1973, 107(1):13-34.

[5] BLACK H D. An easily implemented algorithm for the tropospheric range correction [J]. Journal of Geophysical Research Atmospheres, 1978, 83(B4):1825-1828.

[6] LEANDRO R F, LANGLEY R B, SANTOS M C. UNB3m_pack: a neutral atmosphere delay package for radiometric space techniques [J]. GPS Solutions, 2008, 12(1):65-70.

[7] PENNA, NIGEL, DODSON, et al. Assessment of EGNOS tropospheric correction model [J]. Journal of Navigation, 2001, 54(1):37-55.

[8] 李薇, 袁運斌, 歐吉坤,等. 全球對流層天頂延遲模型IGGtrop的建立與分析[J]. 科學通報, 2012, 57(15):1317-1325.

[9] LI W, YUAN Y, OU J, et al. New versions of the BDS/GNSS zenith tropospheric delay model IGGtrop [J]. Journal of Geodesy, 2015, 89(1):73-80.

[10] 姚宜斌, 胡羽豐, 余琛. 一種改進的全球對流層天頂延遲模型[J]. 測繪學報, 2015, 44(3):242-249.

[11] YAO Y, XU C, SHI J, et al. ITG: A new global GNSS tropospheric correction model [J]. Scientific Reports, 2015, 5(5):10273.

[12] 姚宜斌, 胡羽豐, 張豹. 利用多源數據構建全球天頂對流層延遲模型[J]. 科學通報, 2016(24):2730-2741.

[13] 姚宜斌, 張豹, 嚴鳳,等. 兩種精化的對流層延遲改正模型[J]. 地球物理學報, 2015, 58(5):1492-1501.

[14] MOLLER G, WEBER R, BOHM J. Improved troposphere blind models based on numerical weather ata [J]. Navigation - Journal of The Institute of Navigation, 2014, 61(3):203-211

[15] LAGLER K, SCHINDELEGGER M, BOHM J, et al. GPT2: Empirical slant delay model for radio space geodetic techniques [J]. Geophysical Research Letters, 2013, 40(6):1069.

[16] BOHM J, MOLLER G, SCHINDELEGGER M, et al. Development of an improved empirical model for slant delays in the troposphere (GPT2w) [J]. GPS Solutions, 2015, 19(3):433-441.

[17] 丁茂華, 胡伍生. 一種優化的基于神經網絡的經驗ZTD模型[J]. 測繪通報, 2017(1):22-25.

[18] 胡伍生, 張志偉. 模型誤差補償的神經網絡方法研究[J]. 測繪科學, 2010(增1):47-49.

[19] 崔珊珊. 遺傳算法的一些改進及其應用[D]. 合肥：中國科學技術大學, 2010.

[20] 尹為松, 陶庭葉, 鄧清軍,等. 遺傳算法優化的GPS對流層延遲內插算法[J]. 測繪科學, 2016, 41(1):180-184.