基于中國剩余定理的秘密共享方案*

李潔平，韋性佳

0 引 言

秘密共享是密碼學的一個重要工具。1979年，Shamir[1]和Blakley[2]兩人分別基于拉格朗日多項式和射影幾何理論，提出了兩種不同的秘密共享方案，對現代密碼學的研究具有非常重要的作用。之后，有關秘密共享方面的研究成為許多研究者的課題。1983年，Asmuth和Bloom[3]等人基于中國剩余定理提出了一種的新秘密共享方案。該方案結構簡明，理論知識容易理解，且較Shamir的秘密共享方案效率更高。

1985年，Chor等人[4]第一次提出可驗證的理念,并且構造了一種可驗證的秘密共享方案。1992年，Pedersen[5]提出了一種更方便和實用的秘密共享方案。但是，早期的秘密共享方案存在計算量大、效率相對較低等問題。直到Neal Koblitz[6]等人發現在有限域上橢圓曲線離散對數問題（ECDLP）是難解問題后，橢圓曲線（Elliptic Curve，簡稱ECC）就以它計算量小、效率較高等優勢快速成為密碼學研究的一個重要工具。2005年，Qing.L[7]等人提出了一個基于中國剩余定理的可驗證秘密共享方案。該方案只有在秘密分發者誠實的情況下，檢測出參與者之間的欺騙。

1997年，Anderson[8]首次提出前向安全性理論（Forward Security）；2001年，Itkis和 Reyzin[9]提出一種前向安全簽名方案，實現了有效的簽名驗證和存儲，但效率相對較低。2002年，Kozlov[10]等人利用一種快速更新算法，提出了一種前向安全的簽名方案，不僅周期短，而且適合移動計算。目前，國內學者對前向安全性理論也做了大量研究，如王彩芬等人[11]提出的具有前向安全性的秘密共享方案,基于有限域上離散對數難解問題（ECDLP）和強RSA假設，有效實現了秘密的前向安全性，且具有很強的實踐價值。本文方案在已有秘密共享方案[12-14]研究成果的基礎上，提出了一種基于中國剩余定理的可驗證方案，利用橢圓曲線計算量小、效率高的優勢，減少了方案的運算成本，同時方案基于強RSA假設[15-16]，實現了方案的前向安全性。

1 預備知識

1.1 橢圓曲線離散對數問題（ECDLP）

給定有限域GF(q)上的橢圓曲線E和生成元P∈E(GF(q))，且階為q，對?Q∈〈P〉，尋找a∈[0,q-1]，使得Q=aP，稱為橢圓曲線離散對數問題。

1.2 雙線性變換

定義1：設(G1,+)和(G2,+)是2個階為素數p的循環群，其中前者為加法群，后者為乘法群。令g為G的生成元，如果滿足以下性質，則稱變換e∶G1×G1→ G2為雙線性變換：

（1）雙線性。對任意P1、P2和Q∈G1，有：

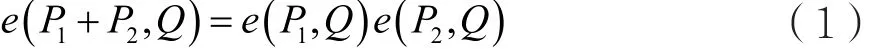
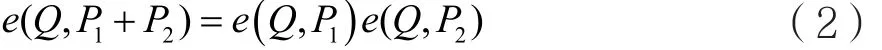
（2）非退化性。存在P∈G1即e(P,P)≠1，即e(P,P)是G2的生成元。

（3）可計算性。對任意P1、P2∈G1，存在有效的算法計算e(P1,P2)。

1.3 中國剩余定理（孫子定理）

給定一組兩兩互素的正整數m1,m2,…,mk和整數c1,c2,c3,…,ck，則同余方程組為：

對于模M具有唯一的解：

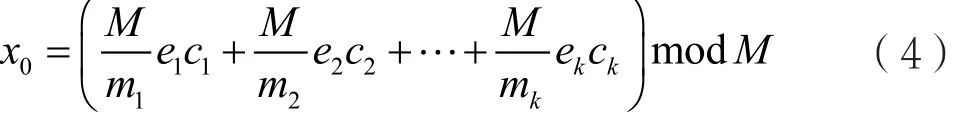
其中：

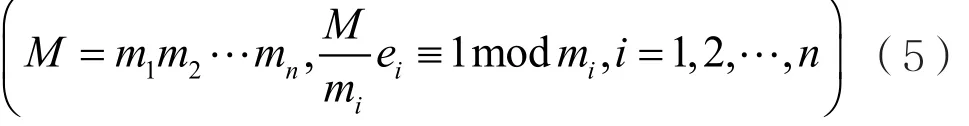
1.4 前向安全性理論

前向安全性理論（Forward Security Theory）具體如下：（1）Pi(i=1,2…n)將S的有效期分為T個時間段，1,2…T；（2）在整個有效期內，公鑰PKU不變，但第j個時間段私鑰SKU隨著時間段j的改變而變換；（3）第j個時段時，Pi計算Sj=f (Sj-1)，其中f是一個單向函數；（4）算出Sj后，立即刪除Sj-1，這樣即使攻擊者A獲得了第j個時間段的Sj，也不能獲得關于S0,S1,…,Sj-1的任何信息，如圖1所示。

圖1 密鑰更新流程

1.5 系統中的記號與參數

P：參與者符號，而Pi為第i個參與者，有Pi∈ P,i=1,2,…,n；

D：秘鑰分配者，且D?P；

K：要分享的秘密（初始者）。

2 提出方案

2.1 系統初始化

（1）D選擇mi∈i=1,2,…,n 且 (mi,mj)=1,mi為素數；選擇初始共享秘密x0∈

（2）計算如下參量：

①秘密份額：

（3）公開系統公鑰：

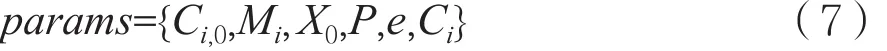
將(ci,0,mi,0)作為私鑰份額通過秘密通道發送給用戶Pi。

2.2 子秘密的更新

當Pi收到初始私密份額(ci,0,mi,0)后，計算ci,j=作為第j個時間段的子份額，然后立即刪除, j=1,2…T。

2.3 秘密的驗證

2.3.1 初始階段秘密的驗證

Pi選擇ki,0∈RZ*q，計算初始公鑰：

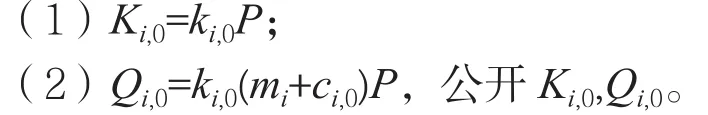
然后，進行D驗證：

若等式成立，則Pi誠實的；同樣，Pi通過等式可驗證D的份額(ci,0,mi,0)是有效的。

2.3.2 驗證更新子秘密

這個階段，用戶Pi通過下面過程研究第j個時間段秘密份額的有效性：

然后，驗證 e ( P , Qi,j) =?e( Mi, Ki) e( Ci, Ki)。若等式成立，D可以驗證Pi更新子秘密的正確性，而Pi也可以驗證D的誠實性。

3 秘密恢復

第j個時間段，所有用戶{P1,P2,…,Pn}利用自己的秘密份額(ci,j,mi)，合作完成如下過程：

（1）計算 M=m1m2…mn；

（3）利用中國剩余定理，計算第j個時間段的共享秘密：

當秘密恢復成員計算出共享秘密后，計算：

（1）得到第j個時間段的共享秘密xj；

（2）利用式（9）中的共享秘密xj和系統公鑰X，驗證等式：

若等式成立，則說明恢復的共享秘密是有效的。

4 正確性及安全性分析

4.1 方案的正確性

定理1：方案在初始階段秘密驗證了Pi和D是誠實的，即等式（8）正確。

證明：根據已知條件，有：

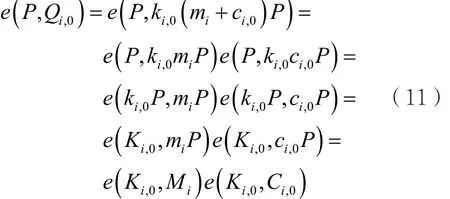
等式成立。

證明：根據已知條件，有：

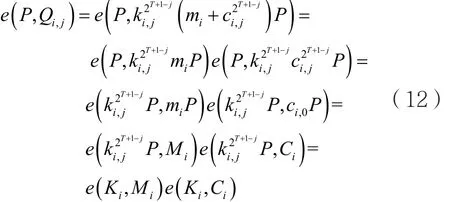
等式成立。

定理3：方案中秘密恢復的驗證是正確的，即等式（10）正確。

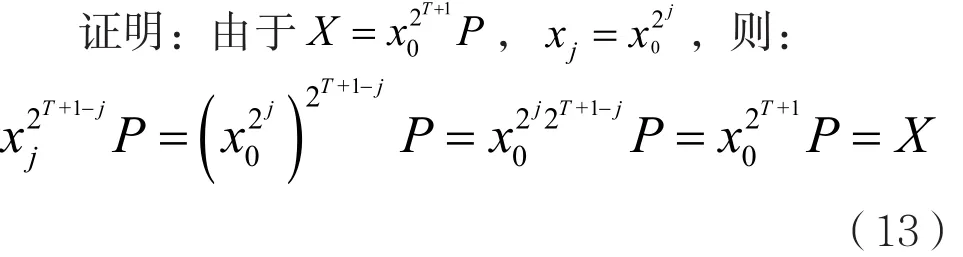
等式成立，所以恢復的秘密是正確的。

4.2 方案的安全性

定理4：公鑰{Ci,0,Mi,Xj,Ci,Ki,Qi,j}不會泄露私鑰{ki,j,ci,j,mi,xj}的任何信息。

證明：若敵手已知 Ci,0、Mi、Ci、Ki、Qi,j想獲取私鑰ki,j、ci,j、mi，由于Ki,j=ki,jP，Ci,j=ci,jP，Qi,j=ki,j(mi+ci,j)P，Mi=miP，則必須解決橢圓曲線離散對數問題。但是，ECDLP是難解決的。所以，敵手無法通過公鑰獲取得到私鑰的任何信息。

定理5：方案具有前向安全性

假設敵手已經掌握第j個時間段的共享密鑰xj,想要獲取前j個時間段的共享秘密xl,l=0,1,…, j-1，有兩種方式：

（1）若想通過Xl=xlP解出xl，必須解決橢圓曲線離散對數問題。但是，ECDLP是難解決的。所以，敵手無法獲得前j個時間段xl；

5 結 語

本文利用中國剩余定理，提出了一種具有前向安全的可驗證秘密共享方案。該方案的創新之處在于：在秘密更新階段，將強RSA問題融入子秘密的更新即，每個用戶利用自己的私鑰通過非交互式的方式更新自己的份額，極大地節省了可信中心的運算量；方案實現了參與者的可驗證性，利用基于橢圓曲線的雙線性對每個時間段的參與者實現互相驗證，這樣可以及時檢測出系統中的欺詐行為，保障系統的安全性。

[1] Shamir A.How to Share a Secret[J].Communication of the ACM 1979,22(11):612-613.

[2] Blakley G R.Safeguarding Cryptographic Keys[C].Proceedings of AFIPS 1979 National Computer Conference,1979:313-317.

[3] Asmuth C,Bloom J.A Modular Approach to Key Safeguarding[J].IEEE Transactions on Information Theory,1983,29(02):208-210.

[4] Chor B,Doldwasser S,Micali S,et al.Verifiable Secret Sharing and Achieving Simultaneity in the Presence of Faults[C].Proceedings of the 26th IEEE Symposium on Foundations of Computer Sciences,1985:383-395.

[5] Pedersen T P.Non-interactive and Informationtheoretic Secure Verifiable Secret Sharing[C].Cryptology CRYPTO’91,1992:129-140.

[6] Koblitz N.Elliptic Curve Cryptosystems [J].Mathematics of Computation,1987,48(48):203-209.

[7] Qiong L,Zhifang W,Xiamu N.et al.A Non-interactive Modular Verifiable Secret Sharing Scheme[C].In ICCCAS 2005:International Conferenc on Communications,Circuits and Systems,2005:84-87.

[8] Anderson R.Two Remarks on Public-key Cryptology[C].Fourth ACM Conference on Computer and Communications Security,1997.

[9] Itkis G,Reyzin L.Forward-secure Signatures with Optimal Signing and Verifying[C].Intenational Cryptology Conference on Advances in Cryptology,2001:332-354.

[10] Kozlov A,Reyzin L.Forward-secure Signature with Fast Key Update[C].International Conference on Security in Communication Networks,2002:241-256

[11] 王彩芬,劉國軍,賈愛庫等.具有前向安全性質的秘密共享方案[J].電子與信息學報,2006,9(28):1974-1976.WANG Cai-fen,LIU Guo-jun,JIA Ai-ku,et al.A Secret Sharing Scheme with Forward Security[J].Journal of Electronics & Information Technolo gy,2006,9(28):1974-1976.

[12] 蘆殿軍,張秉儒,趙海興.基于多項式秘密共享的前向安全門限簽名方案[J].通信學報,2009,30(01):45-49. LU Dian-jun,ZHANG Bing-ru,ZHAO Hai-xing.Forward-secure Threshold Signature Scheme Based on Polynomial Secret Sharing[J].Journal on Communicatio ns,2009,30(01):45-49..

[13] 田有亮,馬建峰,彭長根等.橢圓曲線上的信息論安全的可驗證秘密共享方案[J].通信學報,2008,29(10):45-50.TIAN You-liang,MA Jian-feng,PENG Chang-gen,et al.Information-theoretic Secure Verifiable Secret Sharing Scheme on Elliptic Curve Group[J].Journal on Communic ations,2008,29(10):45-50.

[14] 李慧賢,蔡皖東,裴慶祺.可驗證秘密共享方案的設計與分析[J].西安電子科技大學學報:自然科學版,2008,35(01):148-151.LI Hui-xian,CAI Wan-dong,PEI Qing-qi.Design and Analysis of a Verifiable Secret Sharing Scheme[J].Journal of Xidian University(Natural Science Edition),2008,35(01):148-151.

[15] 汪保友,胡運發.基于強RSA假設的簽名方案[J].軟件學報,2002,13(08):1729-1734.LI Hui-xian,HU Yun-Fa.Signature Scheme Based on Strong RSA Hypothesis[J].Journal of Software,2002,13(08):1729-1734.

[16] 徐文華,賀前華,李韜.基于強RSA假設的數字簽名方案[J].華中科技大學學報:自然科學版,2008,36(12):24-26.XU Wen-hua,HE Qian-hua,LI Tao.Signature Scheme Based Strong RSA Assumption[J].J. Huazhong Univ. of Sci.& Tech.(Natural Science Edition),2008,36(12):24-26.