The value of dual mean Minksowski measure of symmetry at the critical Minkowski points of a convex body

LIU Jianguo，GUO Qi

（School of Mathematics and Physics，SUST，Suzhou 215009，China）

1 Introduction

Let C?Rn（the n-dimensional Euclidean space） be a convex body（i.e.a compact convex set with non-empty interior）.Denote bythe determining family of C，i.e.[1]

One of the important geometric invariants of convex bodies，the Minkowski measure function of asymmetry as∞(·)，is defined by

where “int” denotes the interior(the definition of this form is from[1]，see[2-4]for other equivalent definitions)，and the Minkowski measure of asymmetry as∞（C） of C is so defined as

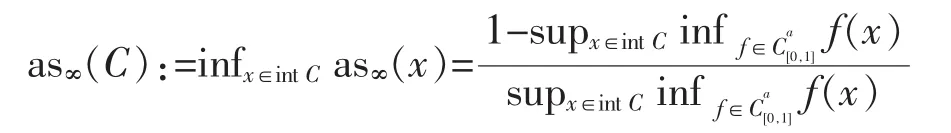
A point x*∈int C such that as∞（x*）=as∞（C） is called a ∞-critical point （or Minkowski-critical point by other authors）.The set of all∞-points of C is called the ∞-critical set of C，denoted by C∞，which is a nonempty closed convex subset of C[2-3].Given x*∈C∞，an f*∈Ca[0，1]satisfying f*（x*） =intf∈Caf（x*） （in turn as∞（C）=[0，1]（1-f*（x*））/f*（x*）） is called a critical function of C with respect to x*（w.r.t.for brevity）.Denote by C*∞（x*） the set of critical functions of C w.r.t.x*（in general C*∞（x*） varies as x*varies）.Observe that，for any f*∈C*∞（x*），

There are numerous generalizations，extensions of the Minkowski measures （see[8-11]and the references therein），among which Toth's work in[6]，Guo and Toth's work in[7]are of particular value.The measures they defined provide information not only for the convex bodies themselves but also for their low dimensional sections or orthogonal projections.

Given a convex body C∈Kn（the family of convex bodies），for each m≥1，we call a multi-set{f0，…，fm}?Ca[0，1]（repetitions are allowed） an m-support configuration of C i{fi≤0}=?，where{fi≤0}：={x∈Rn|fi（x）≤0}.The family of m-support configurations of C is denoted byEom=ECo，m.Then we have the following definition[7，12].

Definition 1Let C∈Kn.For m≥1，its m-th dual mean Minkowski measure fucntionint C→Ris defined by

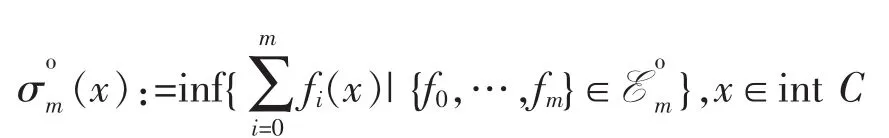
A point x*∈int C satisfyingis called a σom-critical point of C.Denote by Comthe set of-critical points of C.It is easy to check that Comis a closed convex subset of C[7].

Both ∞-critical points and σon-critical points are of some interesting properties[3，13].So it is meaningful to provide methods in finding these critical points.There are already some practical criterions for detecting the∞-critical points，however，there are not many for the σom-critical points.Fortunately，some clues lead to a Conjec-ture：for any C∈Kn，

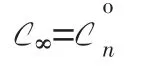
This conjecture is still open.One of the important steps for confirming this conjecture is to find the precise value of σonat the ∞-critical points.So，in this paper，we give explicit value of σonat the∞-critical points in terms of the Minkowski measure of asymmetry.

For notation and terms unmentioned above we refer to[14-15].

2 Critical n-support configurations

In this section，we focus on the nth dual mean Minkowski measures and show the existence of some particular n-support configurations.

Definition 2Let C∈Knand x*∈C∞.If{f0，…，fn}∈Eonsatisfies fi∈C*∞（x*），then{f0，…，fn}is called a critical n-support configuration of C （w.r.t.x*）.

The following is the main result of this section.

Theorem 1Let C∈Kn.For each x*∈C∞，there is at least one critical n-support configuration w.r.t.x*.

To prove Theorem 1，some more preparations are needed.First，we rewrite （3.1） and （3.2） in[3]as one lemma with our notation.

Lemma 1[3]Let C∈Knand x*∈C∞.Then

To see Lemma 1 is indeed equivalent to （3.1） and （3.2） in[3]，one needs only to observe that a closed half space G belongs to the family W appearing in[3]iff G={f≤0}for some f∈C*∞（x*）.

Then，we show a theorem of Helly's type for families of half spaces，which，besides being needed in the proof of Theorem 1，is of its own significance.Some notation and terminologies first：recall that a function f：Rn→Ris affine iff there is a unique （u，b）∈Rn×Rsuch that f（·）=〈u，·〉+b and that f is invertible iff u≠o，where “o” denotes the origin or zero vector.A family{fi}i∈Λwith fi（·）=〈ui，·〉+bi，where Λ is any nonempty index set，is called compact if{（ui，b）}i∈Λis compact inRn×R.

Theorem 2Given C∈Kn.Let{fi=〈ui，·〉+bi}i∈Λ?Ca[0，1]be compact.Then，the following statements are equivalent：

（2）For each u∈Rn，〈ui，u〉≤0 for some i∈Λ.

（3）The origin o∈ri（conv{ui0，…，uil}for some afinely independent ui0，…，uil，1≤l≤n，i.e.，there are positive

（4）cone{ui0，…，uil}=lin{ui0，…，uil}for some afinely independent ui0，…，uil，1≤l≤n.

Lemma 2Let fi（·）=〈ui，·〉+bi，i=0，1，…，m be non-trivial affine functions.Then，for any （um+1，bm+1）∈cone{（u0，b0），…，（um，bm）}，we have

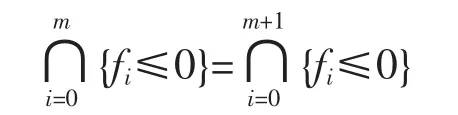
Proof.，then the equality is obvious.If，then this is just a reformulation of the well-known generalized Farkas lemma[15].

Proof of Theorem 2We point out first that{（ui，bi）}i∈Λ?Rn×Ris compact iff both {ui}?Rnand{bi}?R are compact.

（2） ? （3）：Consider the linear space V：=cone{ui}i∈Λ∩（-cone{ui}i∈Λ）.If V={0}，then by the separation theorem for closed cones （cone{ui}i∈Λis closed since{ui}i∈Λis compact），there is u∈Rnsuch that{ui}i∈Λ∈{x｜〈u，x〉＞0}，which contradicts （2）.So dimV≥1.Now，it's easy to see by induction that V=cone{ui0，…，uis}for some ui0，…，uis（1≤s≤n）.

Thus，since-ui0∈lin{uis}sk=0=cone{uis}sk=0，we have-ui0=α0′ui0+，which leads to o=We now let l be the smallest positive integer such that

for some ui0，…，uilwith αik＞0 and claim that ui0，…，uilare affinely independent.Suppose ui0，…，uilare not affinely independent，thenfor some （not all zero） βi0，…，βilwith

2.1.1 磷酸氫二鉀用量對多酚提取率的影響 在磷酸氫二鉀乙醇雙水相中,下相由溶解后的磷酸氫二鉀及少量乙醇構成,上相則由乙醇和水構成,易溶于乙醇相的多酚提取出后進入上相．雙水相的形成是磷酸氫二鉀與乙醇爭奪水分子的過程．隨著磷酸氫二鉀用量的增加,鹽對水的束縛能力增強,使上相中乙醇的相對體積分數增加[5]．從圖2可以看出,隨著磷酸氫二鉀用量的增加,總多酚得率先上升后下降,磷酸氫二鉀過少，雙水相萃取能力低,磷酸氫二鉀過多導致多酚進入下相造成損失;在磷酸氫二鉀2.5 g時,多酚的提取率達到最高值．

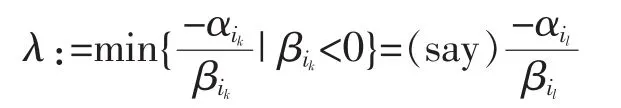
then

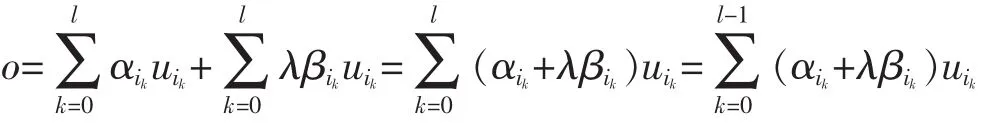
where αik+λβik≥0，（0≤k≤l－1），and at least one of them is positive，a contradiction to the choice of l.It follows from （**） that

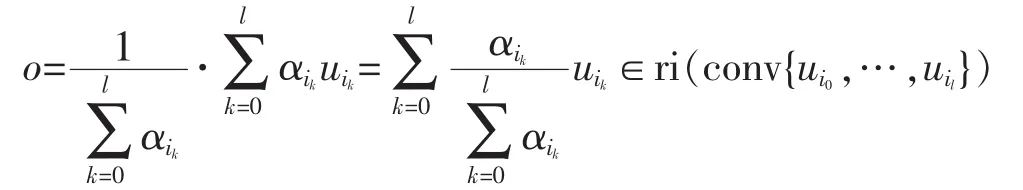
l≤n clearly since ui0，…，uilare affinely independent.

（3）?（4）：Suppose that ui0，…，uil，l≤n，are affinely independent and 0∈ri(conv{ui0，…，uil})，i.e.，with αik＞0.Then for each 0≤k≤l，we have-uikuij∈cone{ui0，…，uil}.Thus lin{ui0，…，uil}=cone{ui0，…，uil}.

（4）?（1）：Suppose lin{ui0，…，uil}=cone{ui0，…，uil}with affinely independent ui0，…，uilfor some 1≤l≤n，with at least one αijpositive.Thus，settingby Lemma 2 we have

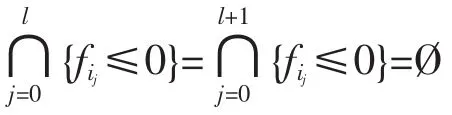
where we used the fact that{fi0≤0}∩{fil+1≤0}=? since{fil+1≤0}?{fi0＞0}which follows from that

Lemma 3Let C∈Knand x*∈C∞.Then both Ca[0，1]and C*∞（x*） are compactly located.

Proof.It was shown that Ca[0，1]is compact （Lemma 1 in[1]）.So we need only to show that C*∞（x*） is closed.Let the sequenceThen f∈Ca[0，1]by the closedness of Ca[0，1]and which implies f∈C*∞（x*）and so C*∞（x*）is closed.

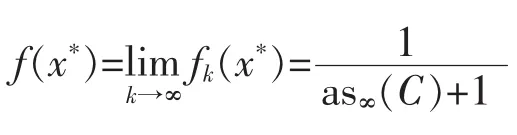
Proof of Theorem 1First，by Lemma 1，Then，since C*∞（x*） is compact by Lemma 3，the origin o∈ri（conv{ui0，…，uil}） for some affinely independent ui0，…，uil，1≤l≤n by （1）?（3） in Theorem 2，where fij(·)：=〈uij，·〉+bij∈C*∞（x*） for some bij∈R.Now，by applying （3）?（1） in Theorem 2 to the family{fij}lj=0，we haveObserving l≤n，we finally obtainfor any fil+1，fil+2，…，fin∈C*∞（x*），i.e.{fi0，…，fil，fil+1，…，fin}is a critical n-support configuration.

3 Main theorem and its proof

In this section，we present our main result：

Theorem 3Let C∈Knand x*∈C∞.Then we have

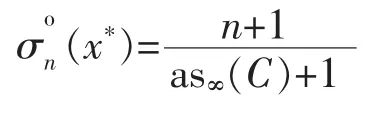
Proof.On one hand，for any n-support configuration{f0，f1，…，fn}∈Eon，fixing an f*∈C*∞（x*），we have by（*） in Section 1，

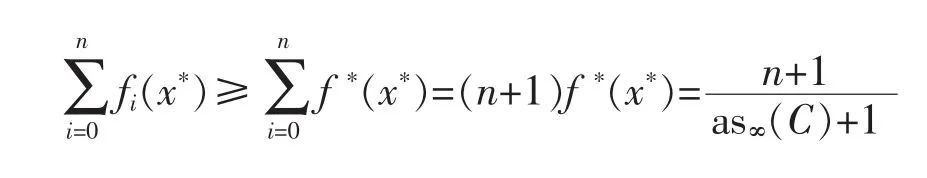
Thus

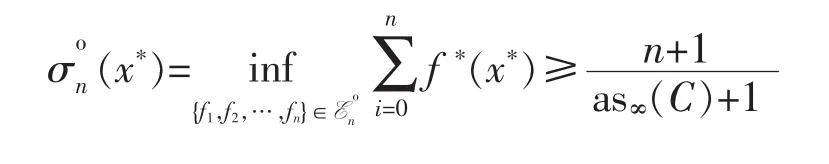
On the other hand，there is a critical n-support configuration{f0*，f1*，…，fn*}by Theorem 2.Thus we have

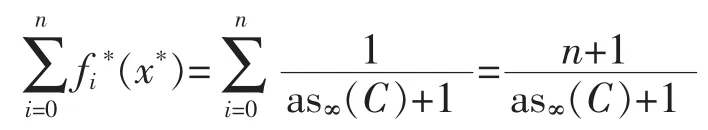
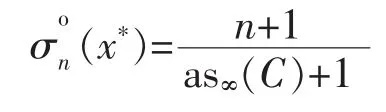
[1]GUO Q.Stability of the Minkowski measure of asym

[2]GRüNBAUM B.Measures of symmetry for convex set[J].Convexity Proceedings of Symposia in Pure Mathematics，1963，7：233-270.

[3]KLEE V L.The critical set of a convex set[J].Amer J Math，1953，75：178-188.

[4]GUO Q，KAIJSER S.On asymmetry of some convex bodies[J].Discrete Comput Geom，2002，27：239-247.

[5]HIRIART-URRUTY J B，LEMARéCHAL C.Fundamentals of Convex Analysis[M].Berling-Heidelberg-New York：Springer Verlag，2001.

[6]TOTH G.Simplicial intersections of a convex set and moduli for spherical minimal immersions[J].The MichiganMathematical Journal，2004，52（2）：341-359.

[7]GUO Q，TOTH G.Dual mean Minkowski measures of symmetry for convex bodies[J].Science China：Mathematics，2016，59（7）：1383-1394.

[8]TOTH G.Measures of symmetry for Convex Sets and Stability[M].New York：Springer，2015.

[9]GUO Q.On p-measures of asymmetry for convex bodies[J].Adv Geom，2012，12：287-301.

[10]GROEMER H.Stability theorems for two measures of symmetry[J].Discrete Comput Geom，2000，24：301-311.

[11]GROEMER H，WALLEN L J.A measure of asymmetry for domains of constant width[J].Beitrage Algebra Geom，2001，42：517-521.

[12]YAO D，GUO Q.Measures of asymmetry dual to mean Minkowski measures of asymmetry for convex bodies[J].Comm Math Res，2016，32（3）：207-216.

[13]GUO Q，TOTH G.Dual mean Minkowski measures and the Grüunbaum conjecture for affine diameters[J].Pacific Journal of Mathematics，2018，292（1）：117-137.

[14]SCHNEIDER R.Convex Bodies：The Brunn-Minkowski Theory[M].2th ed.Cambridge：Cambridge University Press，2014.

[15]HIRIART-URRUTY J B，LEMARéCHAL C.Fundamentals of Convex Analysis[M].New York：Springer Verlag，2001.