基于Matlab的電子式互感器傳變特性仿真研究

金世鑫 , 李 華 , 金曉非 , 李籽良, 耿莉娜

(1.國網遼寧省電力有限公司電力科學研究院，遼寧 沈陽 110006；2.國網遼寧省電力有限公司經濟技術研究院，遼寧 沈陽 110015；3.國網大連供電公司，遼寧 大連 116011)

在實際運行中，電子式互感器體現出相對于傳統互感器的巨大技術優勢，并隨著技術的發展、工藝和設計的改進以及運維經驗的豐富，電子式互感器會得到越來越廣泛的應用。

1 羅氏線圈電流互感器工作原理

基于羅氏線圈電子式電流互感器結構如圖1所示，其基本原理是利用漆包線均勻纏繞在空心骨架上，利用互感原理來測量一次電流的大小，輸出量為電流的微分信號。基于羅氏線圈電子式電流互感器主要分為5個工作單元：傳感單元(羅氏線圈)、電源單元、高壓側數據采集單元、光纖傳輸單元和低壓側合并單元，工作原理如圖2所示[1]。經過羅氏線圈傳感頭的電流信號會轉變成模擬電壓信號，這一電壓信號由高壓側數據采集單元的信號處理電路解析為數字脈沖信號，光電轉換后變換為光信號，光信號通過光纖傳輸單元傳送到低壓合并單元后轉換為電信號,再經放大處理后送入保護系統。其中高壓側數據采集系統中的積分電路是信號處理電路中的極重要環節之一,確保整個測量系統精度的前提便是要保證積分信號的準確。

2 基于Matlab的羅氏線圈電子式互感器傳變特性仿真

2.1 積分電路分析

典型的積分電路包含一階無源積分器、理想有源積分器和負反饋積分器。無源積分電路不包含運放，其在低頻段的工作特性比較差，而在高頻段特性較好，當頻率較低時，并聯電容的容抗值很大，無源積分電路實際就是一個電阻電路[2]。理想積分器結構簡單，但是存在溫漂、電流偏置、電壓失調等問題，這些不利因素不斷積累，會造成信號疊加產生積分漂移，最終導致積分器飽和，失去積分作用。因此，適合作為理論研究，但不具有實用價值。負反饋積分器是在理想積分器的電容上增加一個并聯電阻，其在高頻段特性較好，而在低頻段特性差。但這種積分器在低頻段時對被測信號有放大效果，增益可能遠超工頻信號，工作穩定性差[3]。綜合考慮上述常見各種積分器的優缺點，為了滿足互感器測量寬帶的要求，典型的無源積分電路與有源積分電路級聯組成的級聯積分器得到推廣，電路結構如圖3所示,圖4為繪制的簡單幅頻特性，圖5為級聯積分器與理想積分器的幅頻特性仿真。由圖4可以看出級聯積分器的參數選擇合適的情況下，其幅頻特性連續，性能良好。圖5驗證了圖4得到的結果，進一步證明參數能夠良好配合的級聯積分器有較寬的工作頻帶，在低頻段的頻率特性也不會受到低頻信號的干擾，工作性能良好。

圖1 羅氏線圈結構

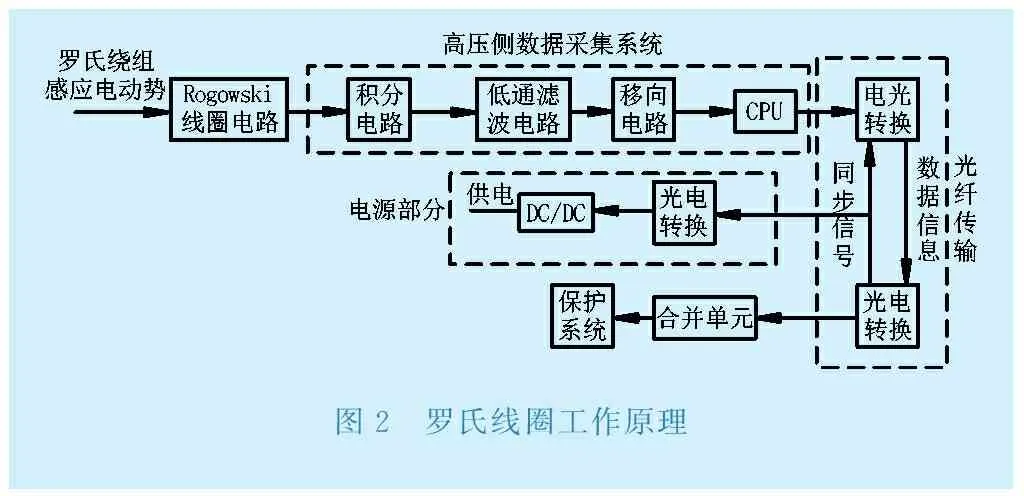
圖2 羅氏線圈工作原理

2.2 低通濾波電路分析

羅氏線圈的輸出電壓難免會受到高頻信號的干擾，為解決這一問題，需要在積分電路后增加濾波電路單元。最常用的低通有源濾波電路有3種，即巴特沃思、切比雪夫和貝塞爾濾波電路[4]。巴特沃思低通濾波器的傳遞函數標準形式為

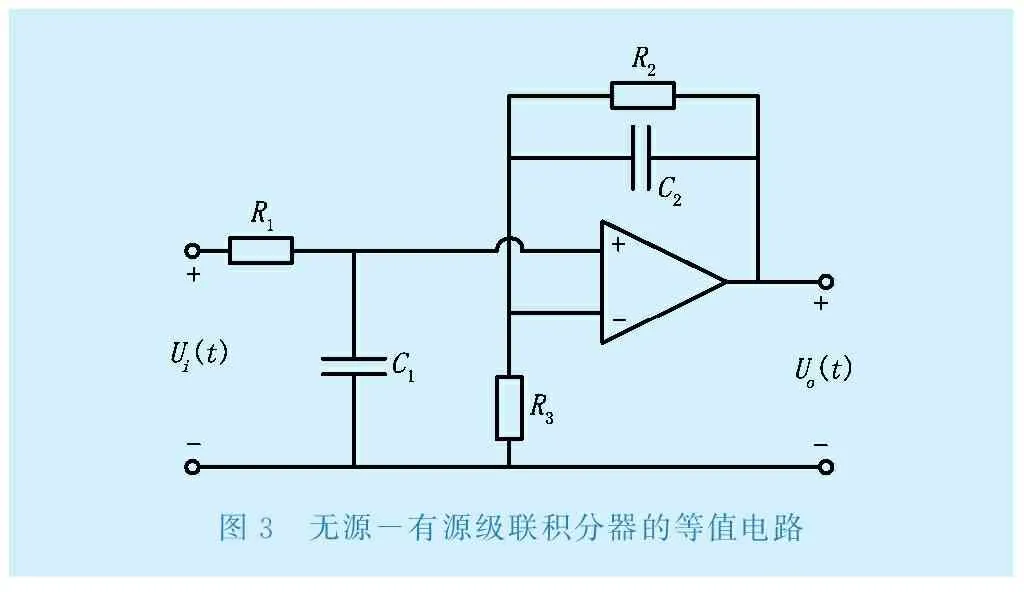
圖3 無源-有源級聯積分器的等值電路

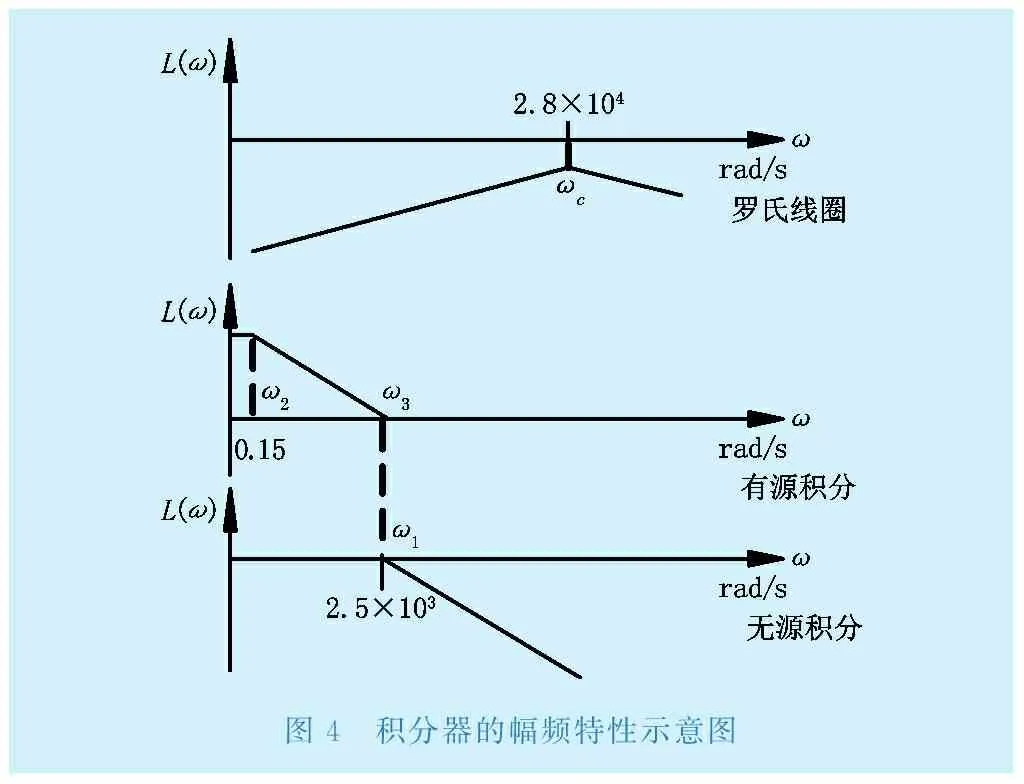
圖4 積分器的幅頻特性示意圖

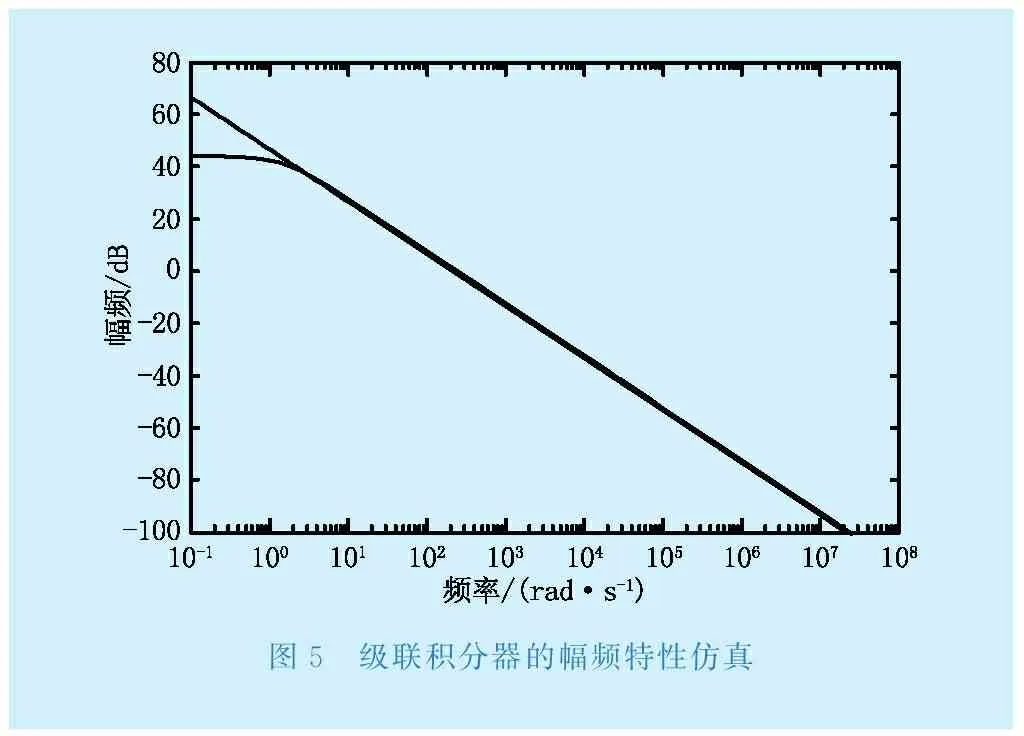
圖5 級聯積分器的幅頻特性仿真

(1)

式中：B、C為巴特沃思歸一化系數，k為增益常數。有源巴特沃思低通濾波器的等值電路如圖6所示。查詢巴特沃思低通濾波器的公式化設計數據表格，設計的參數為C1=10 pF；C2=2.2 nF;R1=110 kΩ；R2=220 kΩ；R3=568.2 kΩ。

利用Matlab中的simulink建立低通濾波器數學模型，低通濾波器的頻率特性如圖7所示，可以看出低通濾波器的幅頻和相頻特性在低頻段很穩定，在高頻段隨著頻率的不斷上升逐漸衰減為零。

圖6 有源低通濾波器的等值電路

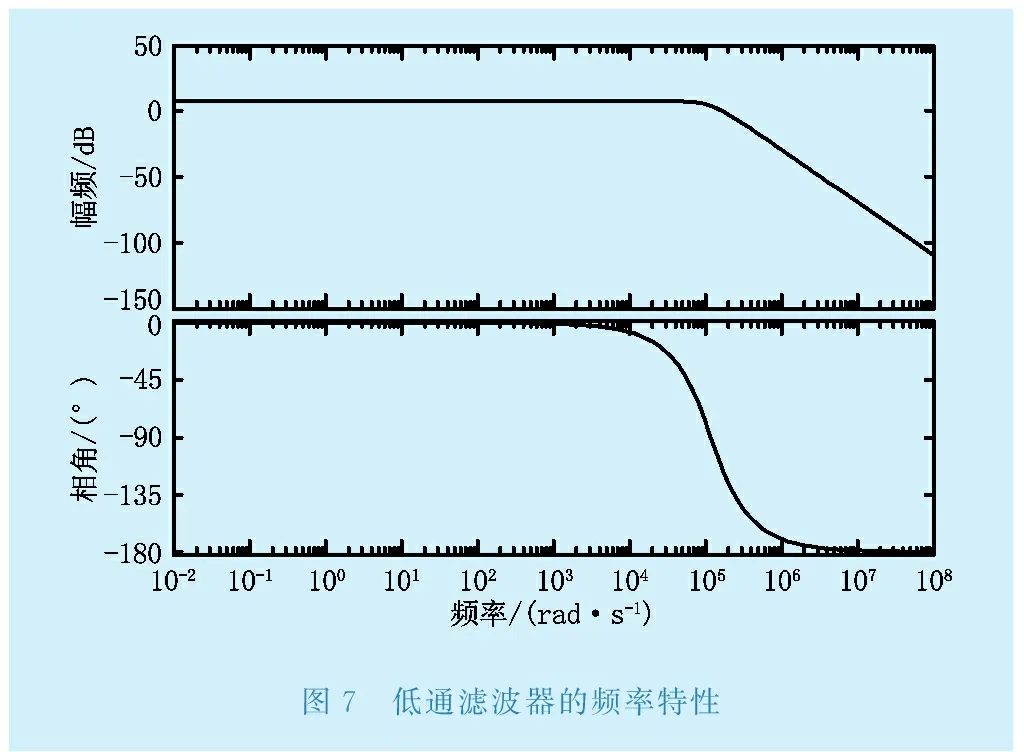
圖7 低通濾波器的頻率特性

2.3 移相電路分析

移相器的作用是在一定頻段內改變傳遞函數的相頻特性，而對其幅頻特性沒有影響，移相器的等值電路如圖8所示，通過圖8可以求得其傳遞函數，通過調節電阻的數值能夠改變移相的角度,為了實現較好的移相效果，需要滿足R2R3=4R1R4且C1=C2，查詢移相器的標準設計參數，確定電容C1、C2的標稱值為0.5 nF。求得各電阻值為R1=7.66 kΩ；R2=10.3 kΩ；R3=21.24 kΩ；R4=7.08 kΩ。利用Matlab中的simulink建立移相器的數學模型,通過仿真得到移相器的頻率特性如圖9所示，從圖9中可以看出在103～107 rad/s頻帶范圍內，移相器具有相位補償的作用，對幅頻特性則沒有影響。

2.4 羅氏線圈電流互感器頻率特性仿真分析

根據電子式電流互感器各環節的工作原理，建立基于羅氏線圈電流互感器的整體仿真模型，如圖10所示。模型中包括羅氏線圈等效電路在內的各個部分是串聯關系[5]。

利用Matlab仿真，得到基于羅氏線圈電流互感器模型的頻率特性如圖11所示。由圖9可以看出，羅氏線圈電流互感器的工作頻帶大概范圍為0.237 ～27 600 rad/s，因此在這段頻率范圍內的幅頻特性是比較穩定的。

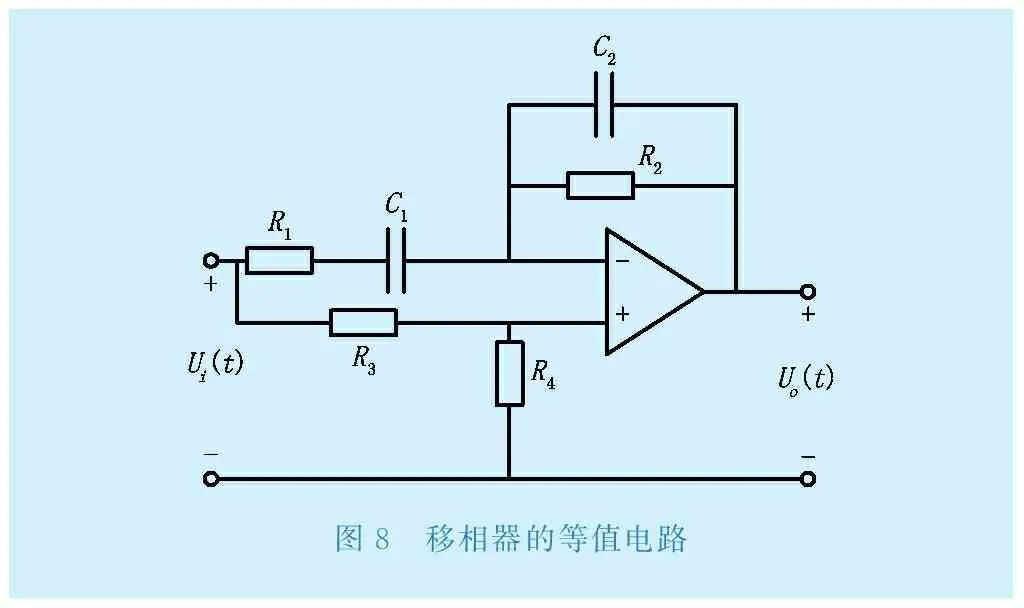
圖8 移相器的等值電路

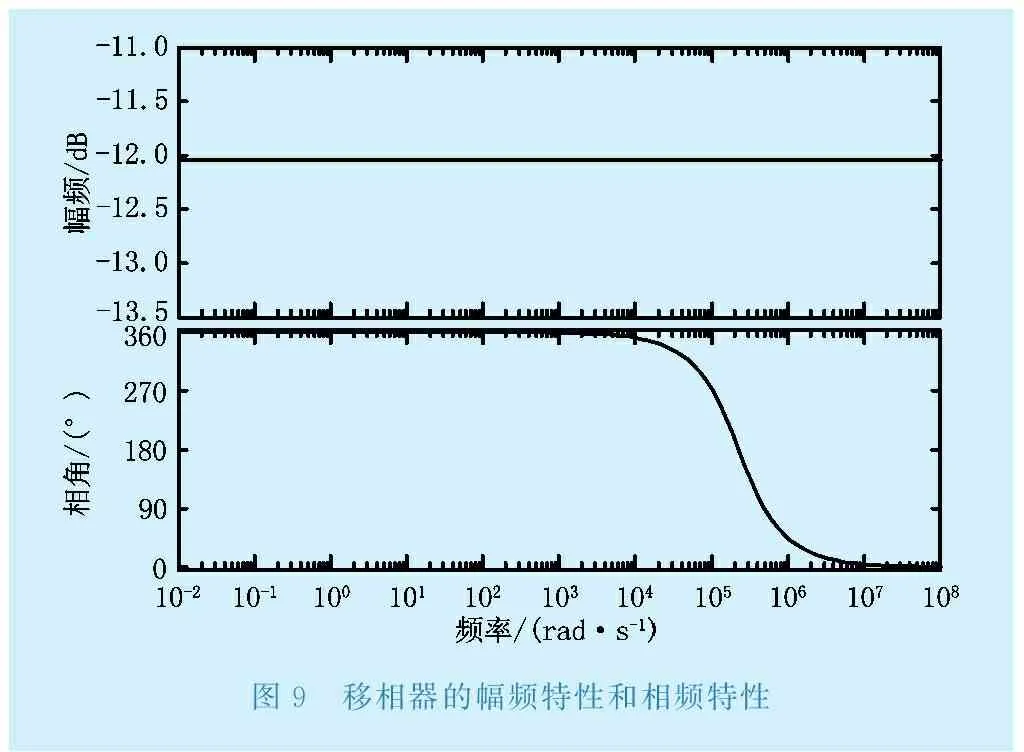
圖9 移相器的幅頻特性和相頻特性

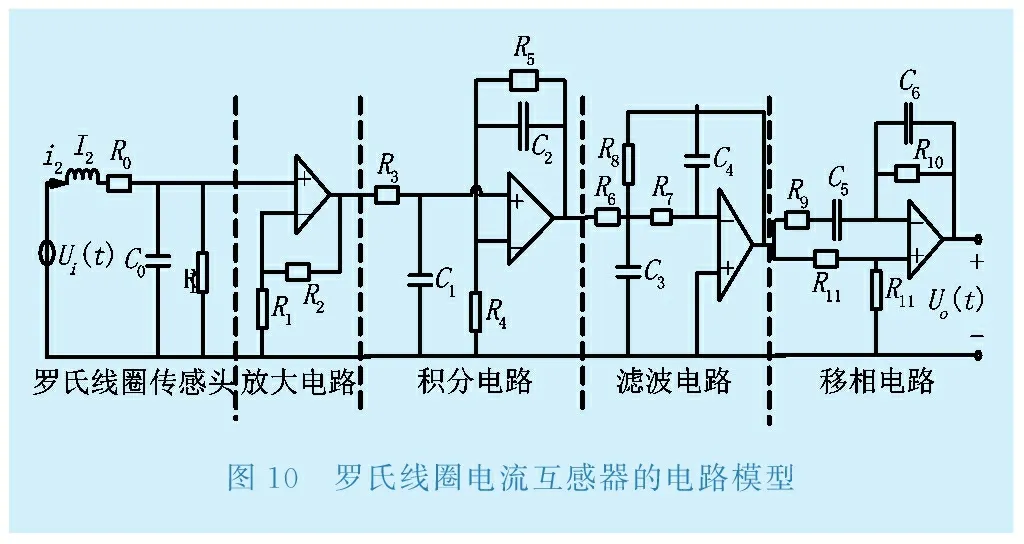
圖10 羅氏線圈電流互感器的電路模型

圖11 基于羅氏線圈的電流互感器的頻率特性

3 積分器參數的優化

電子式電流互感器是智能變電站測量和保護等其他高級應用測試信號的來源，繼電保護系統研究的側重點是電力系統故障后的暫態過程，所以必須分析互感器模型的暫態響應是否可以滿足保護系統的要求。

a. 電力系統發生故障時，通常故障電流包含有穩態電流、衰減交流及衰減直流分量，現以i(t)=e-t/0.1-cos100πt-e-t/0.2sin(200πt)作為輸入電流，通過Matlab中的simulink建立數學模型，仿真分析互感器模型對故障電流的跟隨特性，如圖12所示。由仿真結果可見，該互感器模型能夠反映原故障電流信號，不會發生波形畸變。

圖12 互感器對故障電流的跟隨特性曲線

b. 繼電保護中常需要測量比正常電流值或者故障電流值大很多倍的電流，例如雷擊電流。現模擬8/20 μs的雷擊電流，將其作為羅氏線圈電流互感器的輸入信號，仿真雷擊電流的輸出波形，結果如圖13所示。從圖13中的輸出波形可以看出互感器對雷擊電流的測量并不理想，波形發生畸變且出現時間延遲的現象。

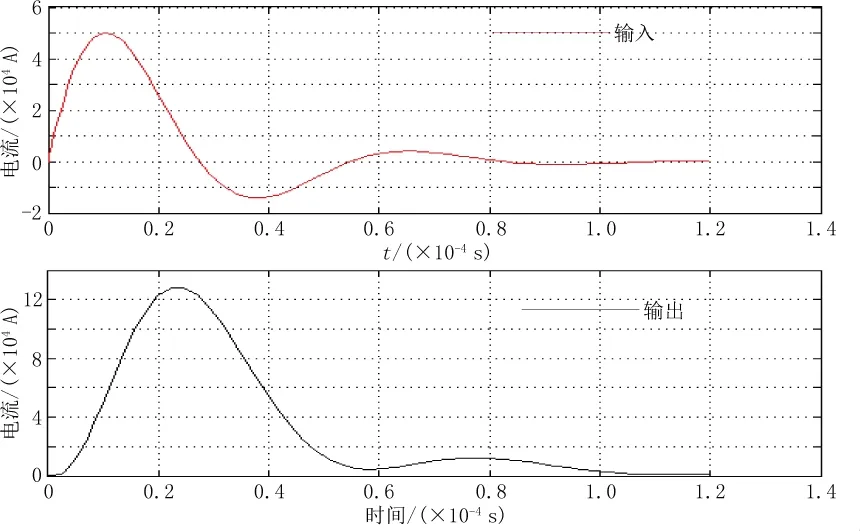
圖13 互感器測量雷擊電流的波形

由于羅氏線圈電流互感器測量的線性度和頻率特性很大程度上決定于積分電路，因此對其積分電路進行分析，對無源-有源級聯積分器參數進行調整。仍然以8/20 μs的雷擊電流作為輸入信號，只改變積分電路的單一參數，其他參數保持不變，仿真分析各個參數變化是對雷擊電流波形的影響，結果如圖14所示。從圖14(a)-(d)分析得出：改變R1,R3,C1,C2都會引起電流波形顯著變化，其中C2和R3的變化對低頻段的影響較大，C1和R1的變化對高頻段的影響較大，根據影響程度大小，改變參數值可解決電流波形恢復問題，為智能變電站高級應用提供精確的原始數據。

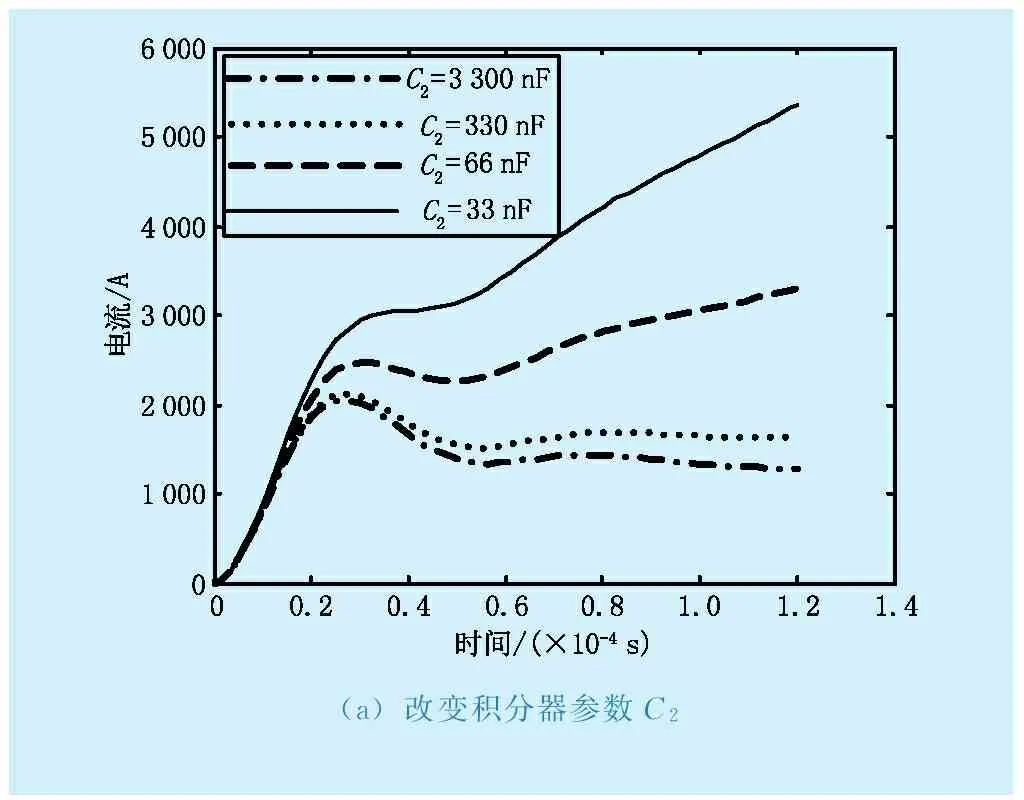
(a)改變積分器參數C2

(b)改變積分器參數R3

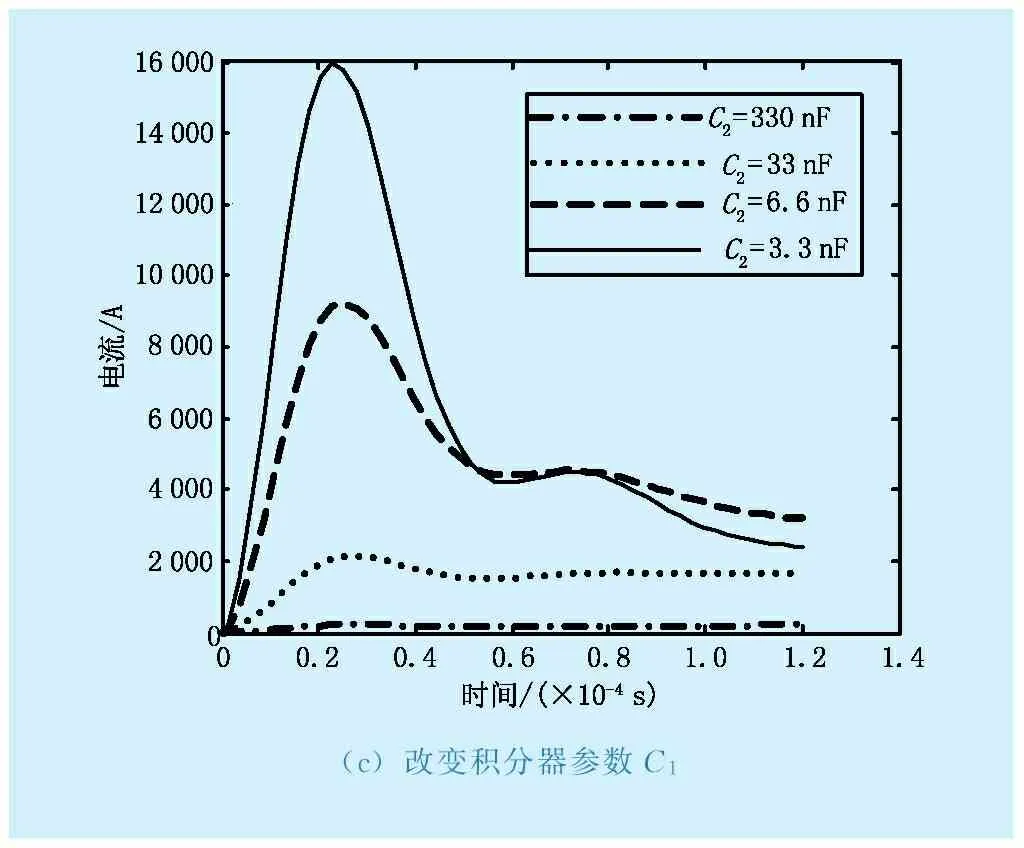
(c)改變積分器參數C1

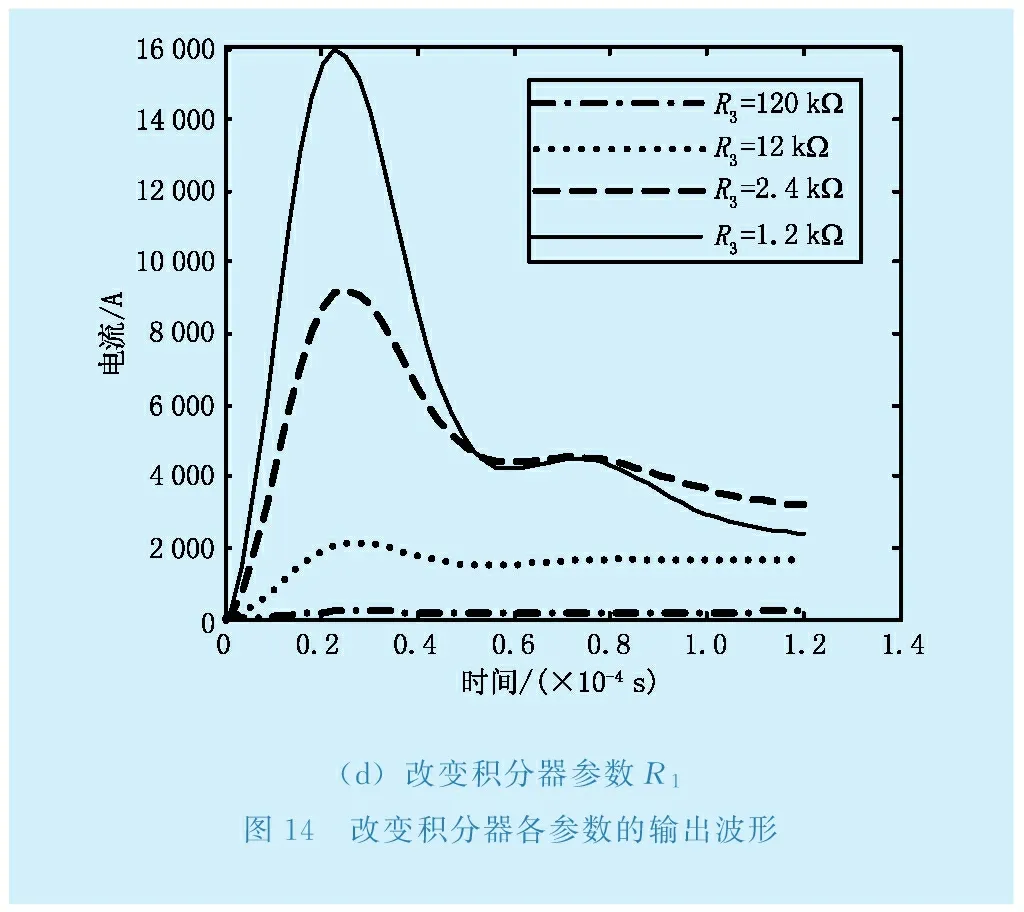
(d)改變積分器參數R1圖14 改變積分器各參數的輸出波形

對無源-有源級聯積分電路參數進行改進，將R1=12 kΩ縮小1 000倍，其他參數保持不變。即：

R1=12 Ω；C1=33 nF;R2=20 MΩ；R3=1.2 kΩ；C2=330 nF。對修改過參數的級聯積分器進行仿真，得到如圖15所示的測量結果。由圖15可以看出波形跟隨效果良好，能夠真實地反映雷擊電流，說明參數優化的有效性。改進后的積分電路如圖16所示，改變R1和C1具有相同的效果，但是選擇改變R1的效果會更好，因為電阻的成本相對電容較低，且電阻受環境條件的影響程度相對電容也較小。

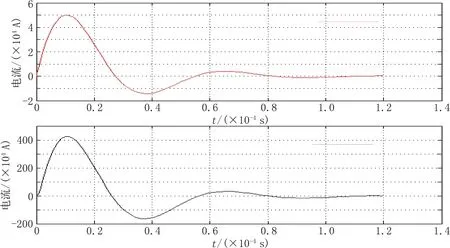
圖15 修改積分器參數后互感器測量雷擊電流的波形

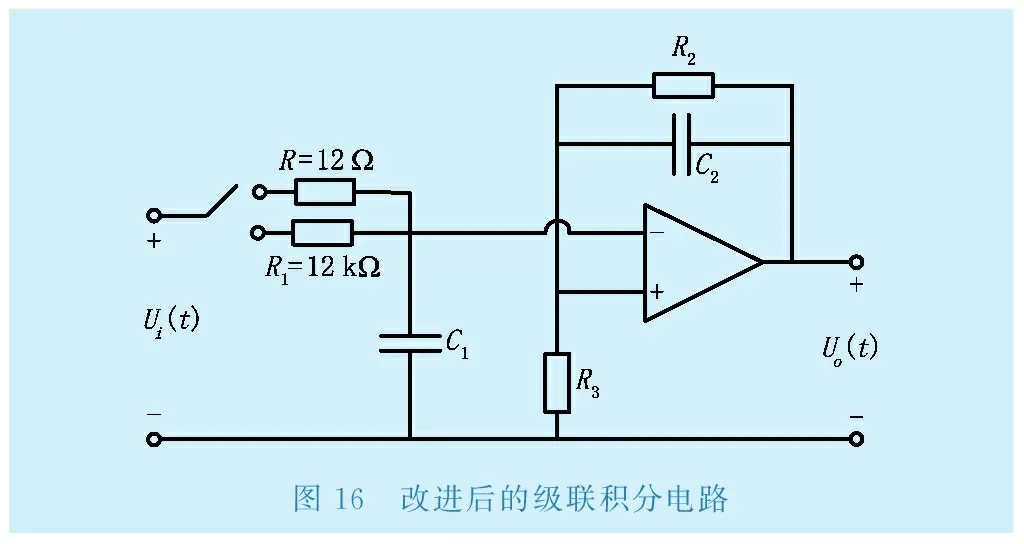
圖16 改進后的級聯積分電路

4 結束語

本文主要研究羅氏線圈電子式互感器的工作原理，對羅氏線圈各主要工作單元(包括積分電路、低通濾波電路和移相電路)的傳變特性進行仿真分析，利用Matlab中的simulink模塊搭建羅氏線圈整體仿真模型，并對其傳變特性進行分析，在此基礎上提出了一種有源、無源級聯積分器，通過仿真找到了積分器傳變特性隨元器件變化的規律，并對積分環節的元器件進行優化，提高了羅氏線圈對雷擊電流傳變的精確度。為互感器運用在故障電流和雷擊測試的理論研究提供一定參考。

[1] 金世鑫,李 華,戴曉宇.電子式互感器的分類和原理綜述[J]. 東北電力技術.2016,37(3)：29-31.

[2] 周有慶,劉 琨,吳桂清,等.基于Rogowski線圈電子式電流互感器的研究[J].電力電氣,2006,25(6):106-110.

[3] 張俊祥，劉立明，尹 明，等.電子互感器的數據還原技術研究[J].東北電力技術.2016,37(10):1-4,8.

[4] 李 偉, 尹項根, 陳德樹,等.基于Rogowski線圈的電子式電流互感器暫態特性研究[J].電力自動化設備, 2008,28(10):34-37.

[5] 王寶誠, 王德玉, 鄔偉揚.羅氏線圈的頻率特性分析與傳感器的設計方法[J].電工技術學報, 2009, 24(9):21-27.