基于拋物線理論考慮多跨竄移時(shí)貨運(yùn)索道運(yùn)行軌跡的研究

文曙東，楊 榮，景文川，馬 青

(1．西南交通大學(xué)土木工程學(xué)院，四川 成都 610031；2. 北京青年政治學(xué)院計(jì)算機(jī)系，北京 100102;3. 四川電力送變電建設(shè)公司，四川 成都 610051)

架空繩索是索道設(shè)備的主要組成部分[1-2]。架空繩索力學(xué)是索道設(shè)計(jì)上不可缺少的基礎(chǔ)知識(shí)。各國(guó)學(xué)者對(duì)懸索基礎(chǔ)理論有不同研究：一種應(yīng)用懸垂曲線理論研究，另一種應(yīng)用拋物線理論研究[3-4]。前者在求懸索精確解方面取得成果，但解超越函數(shù)，在實(shí)際應(yīng)用上存在一定困難。后者計(jì)算理論成熟，運(yùn)算簡(jiǎn)單，在工程上被廣泛應(yīng)用。本文采用拋物線理論分析架空索道是建立在均勻重力場(chǎng)的作用下，對(duì)懸掛纜索做出一些基本假設(shè)。

a. 纜索為理想柔性的，既不能受壓也不能受彎。因?yàn)樗鞯慕缑娉叽缗c索長(zhǎng)相比十分微小。因而界面的抗彎剛度在計(jì)算中可不考慮。索曲線有轉(zhuǎn)折的地方，只要轉(zhuǎn)折曲率半徑不太小，局部彎曲也可不計(jì)。

b. 索的材料符合胡克定律，應(yīng)力與應(yīng)變符合線性關(guān)系。

c. 懸索的橫截面面積及其自重在外荷載作用下的變化量十分微小，忽略不計(jì)。

d. 支撐架為剛性(即沒(méi)有彈性壓縮和彎曲變形)。

e. 纜索與索鞍之間可以滑動(dòng)，并可在塔頂或錨碇處自由滑動(dòng)或轉(zhuǎn)動(dòng)。

根據(jù)第e條，輸變電工程中多跨索道各相鄰跨懸索靠支架及鞍座承托，懸索在支點(diǎn)處可以竄移，主索懸掛在鞍座上，隨著索道加載后受荷懸索拉力增大，鞍座發(fā)生偏擺，若鞍座兩端拉力差大于此時(shí)懸索受到的最大靜摩擦力，可導(dǎo)致懸索在不同跨之間竄移。此竄移量在計(jì)算索道貨物運(yùn)行軌跡時(shí)不能忽略，在計(jì)算某跨貨物運(yùn)行時(shí)索道的軌跡時(shí)，假定該跨前后m跨不考慮鞍座的摩擦力，懸索可以自由竄移，不考慮鞍座的偏擺情況下，本文分析各跨承載鋼絲繩在貨物通過(guò)的運(yùn)行軌跡。另外，當(dāng)懸空架設(shè)鋼索的無(wú)荷中央撓度系數(shù)較小時(shí)，沿懸索曲線的均布荷重與沿弦線的均布荷重兩者之間的誤差是很微小的。此時(shí)，設(shè)懸索自重沿弦線均勻分布，即可導(dǎo)出以代數(shù)函數(shù)法表示的拋物線。在考慮多跨貨運(yùn)索道前后m跨懸索可以自由竄移后，利用拋物線假定，分析貨物的運(yùn)行軌跡對(duì)貨運(yùn)索道在運(yùn)行中判斷貨物是否拖地，具有重要的現(xiàn)實(shí)意義。

1 懸索線型、曲線長(zhǎng)和有荷撓度

無(wú)荷懸索的線型，取決于懸索的撓度(垂度)，撓度是衡量懸索張緊度和線型的尺度，一般以跨中垂度與跨度之比，即中撓系數(shù)S0來(lái)表征懸索的張緊程度。

懸索自重沿水平軸均布的線型任意點(diǎn)的撓度為

(1)

式中：l0為跨度；H0為水平分力；q0為懸索傾斜均布荷重?fù)Q算成的水平均布荷重，即q0=w。

懸索曲線長(zhǎng)度為

(2)

整理后:

(3)

(4)

2 多跨懸索平衡狀態(tài)

當(dāng)索道某跨懸索受到一個(gè)集中荷載作用，前后跨懸索都會(huì)向集中荷載處移動(dòng)。離集中荷載越遠(yuǎn)的鋼索竄移量越小，當(dāng)竄移量小于一定數(shù)值后，竄移將對(duì)鋼索線型和內(nèi)力的計(jì)算基本不產(chǎn)生影響。而集中荷載前后發(fā)生顯著竄移的跨數(shù)m可由試算或者根據(jù)已有工程經(jīng)驗(yàn)給出。在實(shí)際工程中，可以試算多個(gè)m值，根據(jù)計(jì)算結(jié)果按最不利情況進(jìn)行索道設(shè)計(jì)。

本文根據(jù)實(shí)際受力分析，認(rèn)為各跨在竄移后承載繩水平分力相等，以此為條件，建立力的平衡方程，計(jì)算承載繩在鞍座處竄移對(duì)線型的影響。

多跨無(wú)荷懸索示意圖如圖1所示，其最大無(wú)荷拉力產(chǎn)生于最大跨上端支點(diǎn)，若是相同跨距，則產(chǎn)生最大傾角的上端支點(diǎn)。對(duì)于多跨索道，假定各跨在平衡狀態(tài)下，懸索的水平分力相等，各跨中央撓度系數(shù)為

(5)

式中：l1、l2、l3分別為各跨斜距離；S01、S02、S03分別為各跨無(wú)荷中央撓度系數(shù)。

多跨懸索無(wú)荷拉力計(jì)算方法與單跨相同。

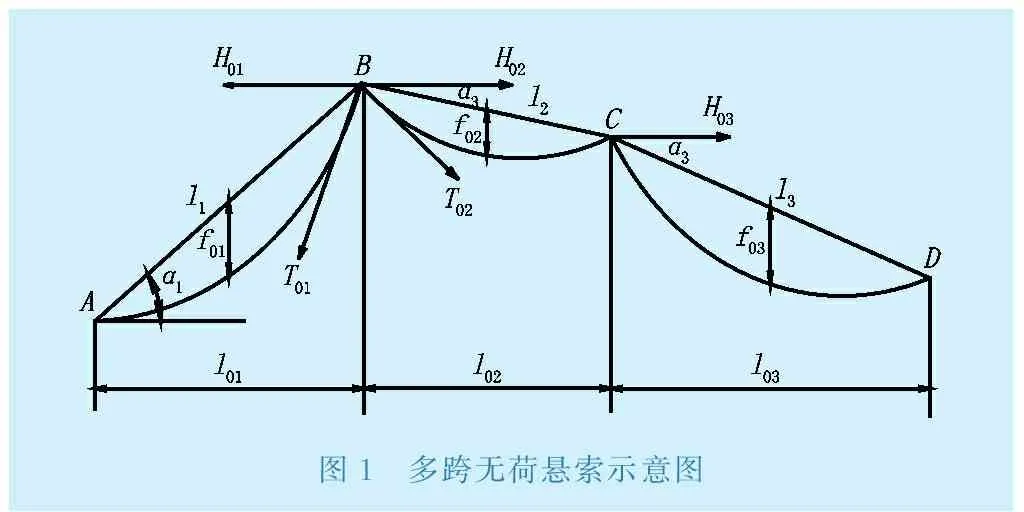
圖1 多跨無(wú)荷懸索示意圖

3 多跨懸索有荷狀態(tài)下的平衡狀態(tài)

貨物在索道運(yùn)行中，由于鞍座兩端索力不平衡，會(huì)導(dǎo)致承重繩在鞍座上的竄移。本文假定貨物在運(yùn)行過(guò)程中，考慮各跨水平力相等，僅考慮m跨可以竄移，來(lái)計(jì)算竄移后的索道運(yùn)行狀態(tài)。

第1步：根據(jù)最大跨設(shè)定的無(wú)荷中撓系數(shù)，假定各跨水平力相等，計(jì)算各跨的無(wú)荷載線型，并計(jì)算出各跨的中撓系數(shù)，無(wú)應(yīng)力長(zhǎng)度。

第2步：考慮前后m跨內(nèi)，計(jì)算荷載P作用在第i跨時(shí)，第i跨的水平力H，無(wú)應(yīng)力長(zhǎng)度。

第3步：考慮前后m跨內(nèi)，非i跨，在水平力為H時(shí)，無(wú)荷載下的無(wú)應(yīng)力長(zhǎng)度。

第4步：考慮前后m跨可以竄移，竄移后各跨的無(wú)應(yīng)力長(zhǎng)度之和。

第5步：對(duì)比第1步相應(yīng)跨的無(wú)應(yīng)力長(zhǎng)度之和，如果第4步計(jì)算出的無(wú)應(yīng)力長(zhǎng)度大于第1步的無(wú)應(yīng)力長(zhǎng)度，表示索道張緊程度偏松，應(yīng)修正H+ΔH，否則修正為H-ΔH，ΔH為迭代步長(zhǎng)。

第6步：修正第2步的第i跨在P作用下的水平力H，重復(fù)第2—5步，直到相應(yīng)跨無(wú)應(yīng)力長(zhǎng)度相差小于一個(gè)很小的給定值為止。就得到考慮前后m跨竄移條件下各跨的狀態(tài)。

4 算例

某送變電建設(shè)工地索道如圖2所示，共3跨，其參數(shù)如下：

第1跨：跨度404 m，高差80.5 m

第2跨：跨度287 m，高差72.5 m

第3跨：跨度200 m，高差36.5 m

承載索數(shù)量：1 個(gè)

承載繩規(guī)格：1670 mmΦ19 mm

無(wú)荷中撓系數(shù)：0.033

吊具重量：1.00 kN

承載索荷載：21.55 kN

支架高度：10 m

圖2 建設(shè)工地索道示意圖

從左到右，對(duì)于跨長(zhǎng)404 m的第1跨，該跨為該建設(shè)工地索道的計(jì)算跨。通過(guò)計(jì)算得到其無(wú)荷載下的線型、不考慮竄移集中荷載點(diǎn)軌跡、考慮1跨竄移和2跨竄移集中荷載點(diǎn)軌跡，如圖3所示。

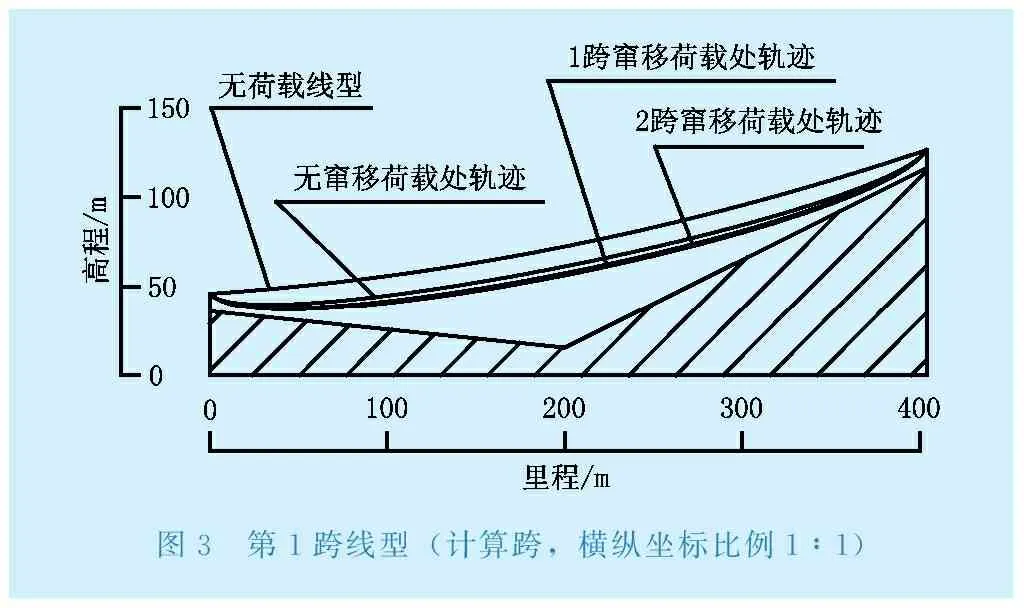
圖3 第1跨線型(計(jì)算跨,橫縱坐標(biāo)比例1∶1)

同樣，計(jì)算出其余兩跨的線型如圖4—圖5所示。由于該建設(shè)工地索道總共為3跨，對(duì)于中間跨，考慮前后1跨竄移和考慮前后2跨竄移是相同的，故其計(jì)算的集中荷載點(diǎn)軌跡也相同。

通過(guò)計(jì)算，對(duì)于該建設(shè)工地索道各跨不考慮竄移、考慮前后1跨竄移、考慮前后2跨竄移的跨中撓度如表1所示。

圖4 第2跨線型

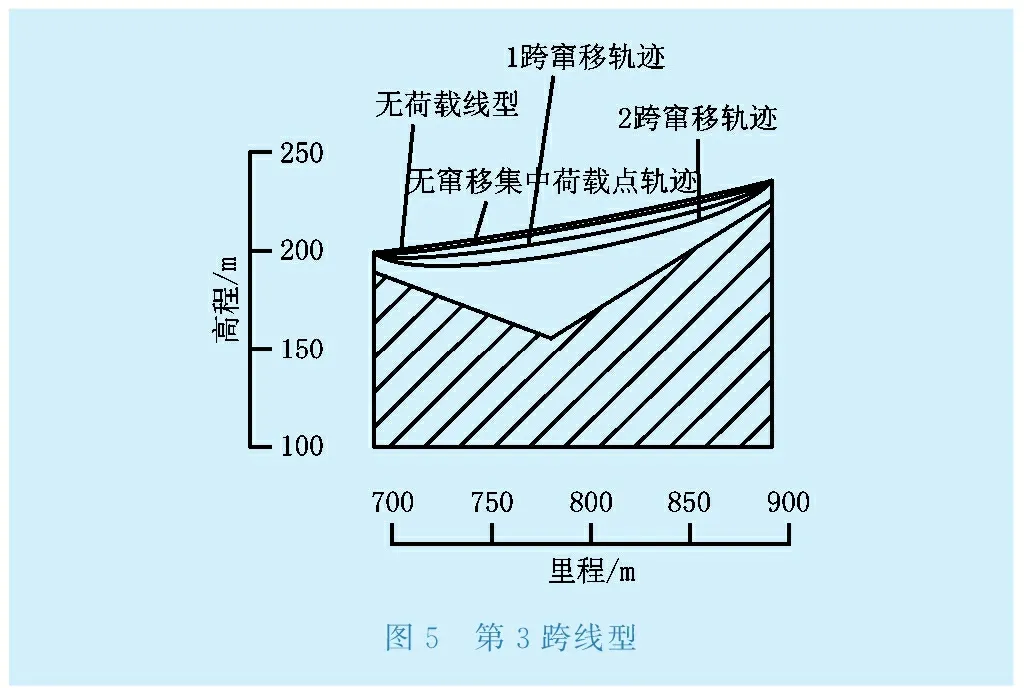
圖5 第3跨線型

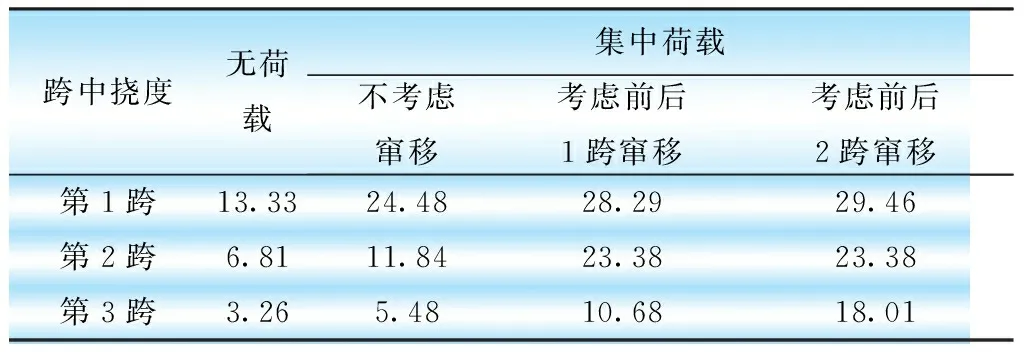
表1 各跨跨中撓度在不同竄移情況下的對(duì)比 m

5 結(jié)束語(yǔ)

當(dāng)集中荷載作用在目標(biāo)跨時(shí)，隨著考慮竄移跨數(shù)的增加，目標(biāo)跨的撓度有相應(yīng)的增加。對(duì)于計(jì)算跨，其撓度增量的相對(duì)值不是很大，對(duì)于非計(jì)算跨，特別是跨度較小的跨，其撓度增量還是比較大的。不考慮鞍座的偏擺和鞍座的摩擦力，懸索可以自由竄移，所以本文計(jì)算的撓度值相對(duì)較大，偏保守。本文考慮目標(biāo)跨前后特定數(shù)量跨度之間存在竄移，間接地考慮了鞍座的摩擦力。通過(guò)本文算例的比較，本文推薦在工程索道中采用考慮前后1跨竄移的計(jì)算方法。該方法簡(jiǎn)單，計(jì)算結(jié)果符合實(shí)際情況，又避免了考慮鞍座摩擦力的繁瑣計(jì)算。

[1] 李志宏. 索道渡槽施工法的應(yīng)用[J]. 東北電力技術(shù)，2005, 26 (5): 24-26.

[2] 張 雷.西藏昌都電網(wǎng)與四川電網(wǎng)聯(lián)網(wǎng)輸變電工程貨運(yùn)索道施工監(jiān)理規(guī)范化管理[J]. 東北電力技術(shù), 2016, 37(12):38-43.

[3] 加藤誠(chéng)平. 林業(yè)架空索道設(shè)計(jì)法[M]. 北京: 農(nóng)業(yè)出版社，1965: 48-183.

[4] 堀高夫 (日) . 懸索理論及其應(yīng)用[M]. 北京: 中國(guó)林業(yè)出版社，1992:7-106.

[5] 馮建祥, 羅才英. 懸索工程[M]. 廈門(mén)：廈門(mén)大學(xué)出版社，2010:2-12.

[6] 官印生，周新年，鄭麗風(fēng)，等. 拋物線理論多跨索道設(shè)計(jì)模型[J]. 起重運(yùn)輸機(jī)械，2007(7): 12-17.