基于合金介電常數的可控特性增強光子自旋霍爾效應?

萬婷 羅朝明 閔力 陳敏 肖磊

1)(湖南理工學院信息與通信工程學院,岳陽 414006)

2)(湖南理工學院物理與電子學院,岳陽 414006)

1 引 言

光子自旋霍爾效應是一種有趣的光束傳輸現象,當光束經過非均勻介質時,由于光子的自旋-軌道相互作用在垂直于入射面的方向會發生光束橫向分離,造成光束自旋分裂的現象[1?5].它是一種類似于電子自旋霍爾效應的現象,其中光子和折射率梯度分別扮演著類似于電子和外加電場的作用.自2004年該現象理論被提出后吸引了許多研究者的興趣,人們對不同物理系統中的光子自旋霍爾效應進行了研究,如高能物理[6,7]、半導體物理[8,9]、超材料[10?13]、光學物理[14?16]等.然而光子自旋霍爾效應是一種非常弱的效應,產生的光子自旋霍爾效應橫移通常只有幾十甚至幾百納米,需要借助弱測量技術才能間接觀測[17].

人們一直在尋找有效的方法來增強光子自旋霍爾效應.研究者發現:在布魯斯特角附近能觀測到大的光子自旋霍爾效應橫移[18,19];不含金屬的多層薄膜結構[20,21]、超表面[13,22,23]也能很好地增強光子自旋霍爾效應.最近的研究發現,含金屬的多層納米結構能夠極大地增強光子自旋霍爾效應[24,25],Zhou和Ling[25]利用BK7玻璃-金-空氣結構激發表面等離子共振(surface plasmon resonance,SPR)使光子自旋霍爾效應橫移達到了3000 nm.然而該結構中使用的金屬為純金屬,介電常數取值有限,而將純金屬以不同比例混合成合金可實現介電常數的人為調控,從而能夠更好地操縱SPR.Yang等[26]利用銀銅合金來調節介電常數從而實現表面等離激元器件性能的優化.張喆等[27]利用金銀合金設計了近紅外SPR傳感器,較大地提高了傳感器的靈敏度.因此,我們相信采用含合金的表面等離激元結構有望進一步增強光子自旋霍爾效應.

本文系統研究了BK7玻璃-合金薄膜-空氣結構中合金介電常數的變化對光子自旋霍爾效應的影響規律,從而找到增強光子自旋霍爾效應的新途徑.首先從平面角譜理論出發,建立高斯光束在BK7玻璃-合金薄膜-空氣結構中反射光的光子自旋霍爾效應模型,進而得到反射光場中的光子自旋霍爾效應橫移表達式.然后探索合金介電常數的變化對光子自旋霍爾效應的影響規律,找到實現光子自旋霍爾效應增強的方法.

2 結構模型與理論

圖1為光束經過BK7玻璃-合金薄膜-空氣結構的反射光自旋霍爾效應模型,BK7玻璃(BK7)、合金薄膜(alloy film)和空氣(air)的介電常數分別為ε1,ε2,ε0.圖中xyz為實驗室坐標系,z軸垂直于分界面,xiyizi和xryrzr分別表示入射坐標系和反射坐標系.光束以入射角θ沿zi方向入射到BK7玻璃-合金薄膜-空氣結構,在z=0(BK7玻璃與合金薄膜界面)處沿zr方向反射時,由于光子自旋霍爾效應的作用,反射光束在垂直于入射面的方向發生橫向分裂,Δy+和Δy?分別表示左、右旋圓偏振分量的橫移.采用高斯光束作為入射,其角譜表達式為

式中w0為光束的束腰寬度;kix,kiy分別表示入射光束的波矢在xi,yi方向上的分量.將任意角譜的高斯光束做傅里葉變換可以得到其電場表達式

式中Ea(xa,ya,za)表示不同光束的電場,其中a=i,r分別表示入射光和反射光;kax,kay,kaz分別為入射光或反射光束的波矢ka在xa,ya,za方向上的分量,將kaz使用泰勒展開化簡,并取前兩項再代入(2)式可得

由電場邊界連續性條件得到反射場角譜與入射場角譜的關系式為[20,25]

圖1 入射光通過BK7玻璃-合金薄膜-空氣結構的反射光自旋霍爾效應模型Fig.1.Schematic of the photonic spin Hall effect in a nanoalloy structure composed of BK7 glass,alloy film,and air.

這里A=p,s;RA為BK7玻璃與合金薄膜界面的菲涅耳反射系數,可由下式表示[28,29]

式中I(xr,yr,zr)∝Sr·erz,即電場強度的分布與坡印廷矢量成正比,坡印廷矢量Sr∝Re[E?r×Hr],其中磁場強度Hr=?ik?1r?×Er,Er為電場強度.通過進一步化簡,反射光的質心橫移表達式可寫為

這里rp,s=|rp,s|exp(iφp,s),|rp,s|表示菲涅耳反射系數的模值,φp,s表示菲涅耳反射系數的相角.

圖2 SPR的共振角隨合金介電常數變化的二維偽彩色圖 (單位 (°))Fig.2.Pseudo-color diagram of the SPR resonant angles changing with the permittivities of alloy film(unit:(°)).

3 數值模擬與分析

本節將依據已建立的反射光自旋霍爾效應模型,研究如圖1所示的BK7玻璃-合金薄膜-空氣結構中合金介電常數的變化對光子自旋霍爾效應的影響規律,進而找出能夠實現光子自旋霍爾效應增強的合金介電常數.在這部分的仿真分析中選取參數如下[20,25]:入射光的波長λ=632.8 nm,BK7玻璃的介電常數ε1=2.295,空氣的介電常數ε0=1,合金介電常數ε2=εr+iεi,其中εr,εi分別為合金介電常數的實部和虛部,合金厚度d=50 nm.由前人的研究[25,29]可知,當光束入射到該結構時p偏振菲涅耳反射系數會隨著入射角的變化發生急劇下降,進而使垂直偏振與水平偏振的菲涅耳反射系數之比迅速增大,相應的光子自旋霍爾效應橫移也急劇增加.究其原因是當光束入射到金屬薄膜表面時自由電子和光子相互作用發生SPR現象的結果.將p偏振菲涅耳反射系數最小值對應的入射角稱為SPR的共振角,該共振角處的光子自旋霍爾效應橫移值為極大值.同時還需要說明的是SPR可由H偏振光激發,而V偏振光幾乎不能激發,故本文只對H偏振情況下的光子自旋霍爾效應進行討論.

為了實現共振角處光子自旋霍爾效應的調控,首先研究了合金介電常數的變化對SPR的共振角的影響規律.參照文獻[25,29]求出不同合金介電常數ε2對應的SPR的共振角,并在此基礎上給出SPR的共振角隨合金介電常數實部εr和虛部εi變化的二維偽彩色圖,如圖2所示,這里的偽彩色圖像的亮度表示SPR的共振角大小.在這里我們設定合金介電常數實部在?12—?2、虛部在0—2.4范心橫移可以表示為[20]圍內變化,從圖2可看出其對應的共振角大約在44°—62°之間,而且SPR的共振角主要受合金介電常數實部的影響,相比而言虛部對共振角的變化影響較小.當合金介電常數虛部εi一定時,共振角隨著合金介電常數實部的增加而增大.下面選取3個不同介電常數ε2=?7.0+0.2i,?5.0+0.2i,?5.0+2.2i進行數值論證,各合金介電常數對應的共振角分別為46.0°,48.2°,47.7°.由此可以看出當實部變化2個單位時共振角變化了2.2°,虛部變化2個單位時共振角僅變化了0.5°.表明合金介電常數虛部相對于實部對共振角的影響較小.

在上述研究基礎上,進一步探索合金介電常數的變化對其共振角處光子自旋霍爾效應的影響規律.將圖2所示的每一對合金介電常數對應的SPR的共振角作為入射角,數值模擬該共振角處光子自旋霍爾效應橫移隨合金介電常數εr,εi的變化,得到的偽彩色圖如圖3所示,亮度表示光子自旋霍爾效應橫移的大小,單位為nm.由圖3可以看出,改變合金介電常數εr,εi能夠實現大范圍內光子自旋霍爾效應橫移的調控,并且共振角處較大的光子自旋霍爾效應橫移隨合金介電常數的變化比較集中,呈帶狀分布.研究還發現最大的光子自旋霍爾效應橫移對應的合金介電常數為ε2=?2.8+1.6i,由Bruggerman理論可知,這一介電常數可以使用金屬Ni,Ag混合得到[30,31]在此結構參數條件下,我們也計算出光子自旋霍爾效應橫移隨入射角θ的變化關系,結果如圖4所示,可以明顯看出在共振角為51.5°時光子自旋霍爾效應橫移最大達到1.2×105nm,這約為文獻[25]中純金屬納米結構BK7玻璃-金-空氣中得到的光子自旋霍爾效應橫移的40倍.產生這種光子自旋霍爾效應增強現象的內在物理機理仍然是光子的自旋角動量和軌道角動量的耦合作用[2,17,32],(10)和(11)式中的exp(±ikryδH,Vr)項就體現了這一耦合,且其隨著|rs|/|rp|比值的增大而增大.為了更加清楚地體現介電常數對光子自旋霍爾效應的調控作用,我們選取最大橫移對應的合金介電常數ε2=?2.8+1.6i和文獻[25]中純金屬金的介電常數ε2=?10.4+1.4i這兩種情形,分別得到了它們的菲涅耳反射系數隨入射角θ的變化關系,結果如圖5所示.從圖5可以清楚地看出,合金結構在其共振角處的菲涅耳反射系數比值|rs|/|rp|遠大于純金屬結構的比值,所選取的合金結構與文獻[25]采用的純金屬結構相比能夠獲得更大的光子自旋霍爾效應橫移.

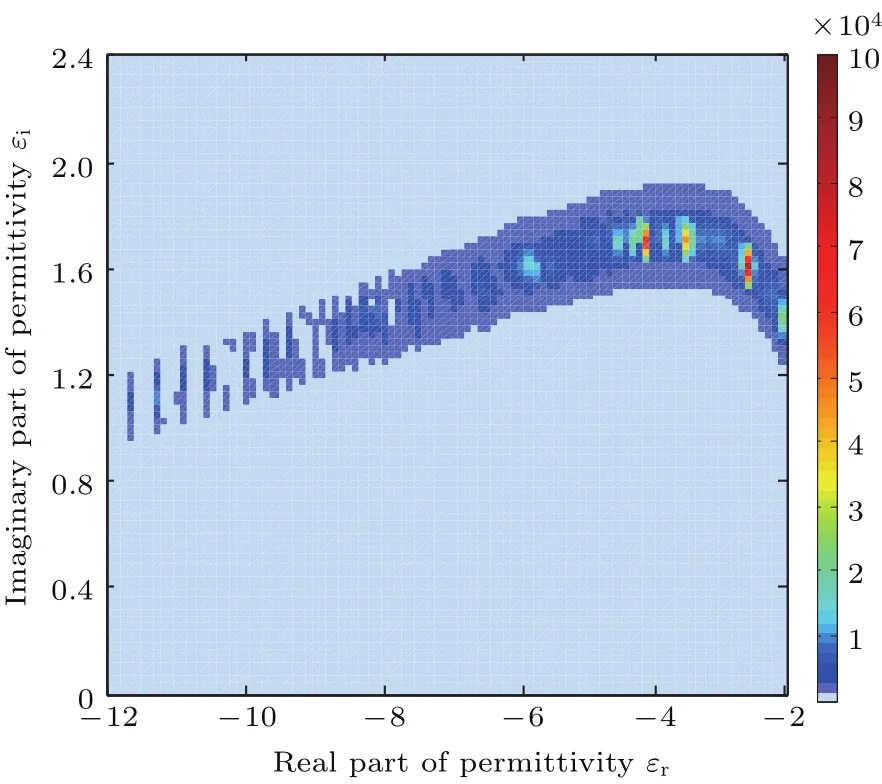
圖3 共振角處光子自旋霍爾效應橫移隨合金介電常數變化的偽彩色圖(單位nm)Fig.3.Pseudo-color diagram of the spin-dependent splitting as a function of the permittivities of alloy film at the resonant angle(unit:nm).

圖4 合金介電常數為ε2=?2.8+1.6i時光子自旋霍爾效應橫移隨入射角的變化Fig.4.The spin-dependent splitting varying with the incident angles under the condition of permittivity ε2= ?2.8+1.6i.

最后保持入射角度恒定不變,探索合金介電常數在該角度處光子自旋霍爾效應的調控規律.為了便于比較,我們將入射角設定為文獻[25]中的最優入射角θ=44.1°,得到該角度下光子自旋霍爾效應橫移隨合金介電常數εr,εi的偽彩色圖,結果如圖6所示,圖中色度表示光子自旋霍爾效應橫移的大小,單位為nm.由圖6可以看出入射角固定為某一定值時光子自旋霍爾效應橫移隨介電常數εr,εi呈軸對稱分布,并以最大值為中心呈球面狀輻射,離中心點越遠光子自旋霍爾效應橫移越小.進一步觀察發現該中心點對應的介電常數ε2=?10.6+1.2i,由Bruggerman理論可知這一介電常數可通過Au和Ag復合制得[30,31].同時給出了該介電常數下光子自旋霍爾效應橫移隨入射角θ的變化關系,結果如圖7所示,可以看出此時光子自旋霍爾效應橫移最大達到8000 nm,與文獻[25]中最大光子自旋霍爾效應橫移值3000 nm相比有了較大的提高.由此可得出當入射角相同時調節合金介電常數能夠進一步增強光子自旋霍爾效應.

圖5 合金納米結構(ε2=?2.8+1.6i)和純金屬納米結構(ε2=?10.4+1.4i)的菲涅耳反射系數隨入射角的變化Fig.5.The Fresnel re fl ection coefficients changing with the incident angle for a nanoalloy structure(ε2= ?2.8+1.6i)and a pure nanometal structure(ε2= ?10.4+1.4i).

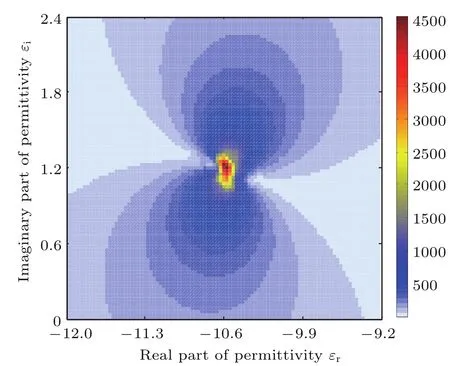
圖6 光子自旋霍爾效應橫移隨合金介電常數變化的偽彩色圖(單位nm)Fig.6.Pseudo-color diagram of the spin-dependent splitting varying with the permittivities of alloy film(unit:nm).

圖7 合金介電常數ε2=?10.6+1.2i時光子自旋霍爾效應橫移隨入射角的變化Fig.7. The spin-dependent splitting varying with the incident angle under the condition of permittivity ε2= ?10.6+1.2i.

4 結 論

本文基于平面角譜理論建立了光束經過BK7玻璃-合金薄膜-空氣結構的反射光自旋霍爾效應模型,系統研究了合金介電常數的變化對光子自旋霍爾效應的影響,找到了實現光子自旋霍爾效應增強的合金介電常數.研究發現,SPR共振角主要受合金介電常數實部的影響,隨著實部的增加而增大,相比而言虛部對共振角的影響較小.當入射角為共振角時,較大的光子自旋霍爾效應橫移隨合金介電常數的變化比較集中,呈帶狀分布.選取介電常數?2.8+1.6i的Ag-Ni合金時得到最大橫移1.2×105nm,這約為純金屬的納米結構BK7玻璃-金-空氣中得到的光子自旋霍爾效應橫移的40倍.當入射角固定為44.1°時,光子自旋霍爾效應橫移隨介電常數的變化呈軸對稱分布,并以最大值為中心呈球面狀輻射,離中心點越遠光子自旋霍爾效應橫移越小.選取介電常數?10.6+1.2i的Ag-Au合金時,最大的光子自旋霍爾效應橫移能達到8000 nm,相比于以往BK7玻璃-金-空氣結構中得到的橫移3000 nm也有了較大的提高.綜上所述,合適地選取合金介電常數,可以有效地增強光子自旋霍爾效應,這些研究結果可以為研制SPR傳感器等新型光學納米器件提供理論依據.

[1]Onoda M,Murakami S,Nagaosa N 2004Phys.Rev.Lett.93 083901

[2]Bliokh K Y,Bliokh Y P 2006Phys.Rev.Lett.96 073903

[3]Hermosa N,Nugrowati A M,Aiello A,Woerdman J P 2011Opt.Lett.36 3200

[4]Gorodetski Y,Bliokh K Y,Stein B,Genet C,Shitrit N,Kleiner V,Hasman E,Ebbesen T W 2012Phys.Rev.Lett.109 013901

[5]Ling X H,Zhou X X,Huang K,Liu Y C,Qiu C W,Luo H L,Wen S C 2017Rep.Prog.Phys.80 066401

[6]Gosselin P,Bérard A,Mohrbach H 2007Phys.Rev.D75 084035

[7]Dartora C A,Cabrera G G,Nobrega K Z,Montagner V F,Matielli M H K,de Campos F K R,Filho H T S 2011Phys.Rev.A83 012110

[8]Ménard J M,Mattacchione A E,van Driel H M,Hautmann C,Betz M 2010Phys.Rev.B82 045303

[9]Alizadeh M H,Reinhard B M 2016Opt.Express24 8471[10]Lee Y U,Wu J W 2015Sci.Rep.5 13900

[11]Yi X N,Li Y,Liu Y C,Ling X H,Zhang Z Y,Luo H L 2014Acta Phys.Sin.63 094203(in Chinese)[易煦農,李瑛,劉亞超,凌曉輝,張志友,羅海陸 2014物理學報 63 094203]

[12]Chen M,Luo Z M,Wan T,Liu J 2017Acta Opt.Sin.37 0226002(in Chinese)[陳敏,羅朝明,萬婷,劉靖 2017光學學報37 0226002]

[13]Liu Y C,Ke Y G,Luo H L,Wen S C 2017Nanophotonics6 51

[14]Luo Z M,Chen S Z,Ling X H,Zhang J,Luo H L 2014Acta Phys.Sin.63 154203(in Chinese)[羅朝明,陳世禎,凌曉輝,張進,羅海陸2014物理學報63 154203]

[15]Qin Y,Li Y,He H Y,Gong Q H 2009Opt.Lett.34 2551[16]Neugebauer M,Grosche S,Rothau S,Leuchs G,Banzer P 2016Opt.Lett.41 3499

[17]Hosten O,Kwiat P 2008Science319 787

[18]Luo H L,Zhou X X,Shu W X,Wen S C,Fan D Y 2011Phys.Rev.A84 043806

[19]Qiu X D,Zhang Z Y,Xie L G,Qiu J D,Gao F H,Du J L 2015Opt.Lett.40 1018

[20]Luo H L,Ling X H,Zhou X X,Shu W X,Wen S C,Fan D Y 2011Phys.Rev.A84 033801

[21]Wang B,Li Y,Pan M M,Ren J L,Xiao Y F,Yang H,Gong Q H 2013Phys.Rev.A88 043842

[22]Tang T T,Li C Y,Luo L 2016Sci.Rep.6 30762

[23]Ling X H,Zhou X X,Yi X N,Shu W X,Liu Y C,Chen S Z,Luo H L,Wen S C,Fan D Y 2015Light Sci.Appl.4 e290

[24]Zhou X X,Xiao Z C,Luo H L,Wen S C 2012Phys.Rev.A85 043809

[25]Zhou X X,Ling X H 2016IEEE Photon.J.8 4801108[26]Yang G,Fu X J,Zhou J 2013J.Opt.Soc.Am.B30 282

[27]Zhang Z,Liu Q,Qi Z M 2013Acta Phys.Sin.62 060703(in Chinese)[張喆,柳倩,祁志美 2013物理學報 62 060703]

[28]Born M,Wolf E 1999Principles of Optics(Cambridge:Cambridge University Press)pp38–44

[29]Salasnich L 2012Phys.Rev.A86 055801

[30]Berthault A,Rousselle D,Zerah G 1992J.Magn.Magn.Mater.112 477

[31]Jiang J J,Li D,Geng D Y,An J,He J,Liu W,Zhang Z D 2014Nanoscale6 3967

[32]Bliokh K Y,Niv A,Kleiner V,Hasman E 2008Nat.Photon.2 748