單向相關(guān)下的機(jī)械零件動(dòng)態(tài)可靠性分析
楊 娜
(蘭州職業(yè)技術(shù)學(xué)院機(jī)電工程系, 甘肅 蘭州 730000 )
應(yīng)力-強(qiáng)度干涉模型是機(jī)械可靠性分析的理論基礎(chǔ),其中的應(yīng)力和強(qiáng)度都是廣義的概念,即廣義應(yīng)力是載荷、振動(dòng)、溫度、噪聲、腐蝕等所有可能導(dǎo)致零部件破壞的因素,屬于外部特性;廣義強(qiáng)度是零部件能夠抵抗破壞的能力,屬于內(nèi)部特性。但傳統(tǒng)的應(yīng)力-強(qiáng)度干涉模型存在兩方面的不足:(1)通常將應(yīng)力與強(qiáng)度視為兩個(gè)隨機(jī)變量,未考慮其隨時(shí)間的變化,由此得到的是靜態(tài)的可靠度;(2)往往假設(shè)應(yīng)力與強(qiáng)度之間相互獨(dú)立。而實(shí)際上,應(yīng)力與強(qiáng)度間存在相關(guān)性,隨著載荷的作用,強(qiáng)度會(huì)逐漸降低。機(jī)械零部件在運(yùn)行過(guò)程中,由于受載荷、振動(dòng)、溫度、輻射、噪聲、腐蝕等外部環(huán)境及其自身材料缺陷、老化、分散性等綜合影響,其實(shí)際工作情況下的應(yīng)力與強(qiáng)度是不確定的,是隨時(shí)間變化的隨機(jī)變量,即為隨機(jī)過(guò)程。因此,應(yīng)力-強(qiáng)度干涉(stress-strength interference,SSI)過(guò)程應(yīng)是一個(gè)動(dòng)態(tài)過(guò)程,相應(yīng)的可靠度也就是隨時(shí)間變化的函數(shù)。
隨著機(jī)械系統(tǒng)和工作環(huán)境日益復(fù)雜化,產(chǎn)品的性能和可靠性需要滿足更高的要求。對(duì)于機(jī)械零件的可靠性預(yù)測(cè)問(wèn)題,國(guó)內(nèi)外大量學(xué)者進(jìn)行了相關(guān)研究。動(dòng)態(tài)與漸變是機(jī)械產(chǎn)品不可避免的隨時(shí)間變化的形態(tài),對(duì)機(jī)械產(chǎn)品進(jìn)行動(dòng)態(tài)與漸變可靠性探究是可靠性研究的遞進(jìn)與升華[1]。文獻(xiàn)[2]運(yùn)用順序統(tǒng)計(jì)量理論以及基于獨(dú)立的SSI模型,建立了以載荷作用次數(shù)為壽命度量指標(biāo)的零件動(dòng)態(tài)可靠度計(jì)算模型。文獻(xiàn)[3]建立了不確定性載荷作用下的零件時(shí)變可靠性模型,給出了基于載荷和強(qiáng)度分布的零件可靠度計(jì)算表達(dá)式。文獻(xiàn)[4]基于結(jié)構(gòu)抗力與載荷效應(yīng)相互獨(dú)立的基本假設(shè),提出了考慮結(jié)構(gòu)動(dòng)態(tài)可靠性的全隨機(jī)過(guò)程模型。文獻(xiàn)[5]分析穩(wěn)定應(yīng)力和沖擊應(yīng)力組成的復(fù)合應(yīng)力,推導(dǎo)了考慮強(qiáng)度退化時(shí)的可靠性模型。上述模型雖然研究的是動(dòng)態(tài)可靠性問(wèn)題,但大多立足于應(yīng)力與強(qiáng)度相互獨(dú)立的假設(shè),因此,對(duì)于應(yīng)力與強(qiáng)度間的相關(guān)性的描述存在明顯不足。文獻(xiàn)[6]考慮組合應(yīng)力下的結(jié)構(gòu)受力情形,分別探討了強(qiáng)度退化與否的動(dòng)態(tài)可靠度。文獻(xiàn)[7]考慮隨機(jī)載荷的加載形式分別為動(dòng)載荷累加、等幅并且服從Poisson分布、載荷隨時(shí)間變化且不服從任何分布的三種情況,利用應(yīng)力-強(qiáng)度干涉理論和隨機(jī)過(guò)程理論建立了結(jié)構(gòu)強(qiáng)度退化情況下的動(dòng)態(tài)可靠性模型。文獻(xiàn)[8]考慮載荷隨時(shí)間變化及強(qiáng)度退化,運(yùn)用隨機(jī)過(guò)程和順序統(tǒng)計(jì)理論,建立變幅隨機(jī)載荷和強(qiáng)度退化下零件的動(dòng)態(tài)可靠性模型。文獻(xiàn)[9]通過(guò)定義次數(shù)等效系數(shù)和參考載荷,分析隨機(jī)載荷作用下強(qiáng)度發(fā)生退化,推導(dǎo)了存在共因失效的零件可靠度計(jì)算模型。上述文獻(xiàn)在一定程度上分析了載荷與強(qiáng)度的相關(guān)性,但其相關(guān)性多基于文獻(xiàn)[10]所提出的剩余強(qiáng)度模型來(lái)體現(xiàn)。在工程實(shí)際中,零部件的強(qiáng)度在不同的應(yīng)力水平下會(huì)有不同的表現(xiàn),也就是說(shuō)強(qiáng)度與應(yīng)力是單向相關(guān)的。所謂應(yīng)力與強(qiáng)度單向相關(guān),是指強(qiáng)度受應(yīng)力特性的影響,并隨應(yīng)力的作用逐漸降低,而應(yīng)力則取決于外部載荷和工作環(huán)境,與強(qiáng)度無(wú)關(guān)。
為評(píng)估零件在應(yīng)力與強(qiáng)度單向相關(guān)下的動(dòng)態(tài)可靠度,本文利用Gamma過(guò)程來(lái)描述隨機(jī)載荷作用,基于經(jīng)典的Miner累積損傷理論,進(jìn)一步推導(dǎo)隨著載荷作用而產(chǎn)生的強(qiáng)度不斷降低的強(qiáng)度退化模型。結(jié)合傳統(tǒng)的應(yīng)力-強(qiáng)度干涉模型,建立零件的動(dòng)態(tài)可靠度預(yù)測(cè)模型。最后通過(guò)算例驗(yàn)證模型的有效性。
1 傳統(tǒng)的應(yīng)力-強(qiáng)度干涉模型
傳統(tǒng)的應(yīng)力-強(qiáng)度干涉模型把應(yīng)力與強(qiáng)度作為兩個(gè)隨機(jī)變量,若使零部件正常工作,則要求其強(qiáng)度大于工作應(yīng)力,否則零部件將遭到破壞。應(yīng)力和強(qiáng)度都應(yīng)該是廣義的概念,廣義應(yīng)力是載荷、振動(dòng)、溫度、噪聲、腐蝕等所有可能導(dǎo)致零部件破壞的因素,屬于外部特性;廣義強(qiáng)度是零部件的抗熱性、耐磨性、抗腐蝕性等能夠抵抗破壞的能力,屬于內(nèi)部特性。可靠度R則是零部件強(qiáng)度δ大于應(yīng)力s的概率P,可以表達(dá)為:
R=P(δ>s)
(1)
將應(yīng)力與強(qiáng)度作為兩個(gè)隨機(jī)變量,可以把式(1)作如下表達(dá)[11]:
(2)
式中:f(s)表示應(yīng)力s的概率密度函數(shù);g(δ)表示強(qiáng)度δ的概率密度函數(shù)。
上述模型是一個(gè)靜態(tài)模型,不能直接應(yīng)用于當(dāng)應(yīng)力與強(qiáng)度隨時(shí)間變化的情況。而事實(shí)上,由于影響零件性能的外部環(huán)境因素是動(dòng)態(tài)的隨機(jī)過(guò)程,應(yīng)力與強(qiáng)度在很多情況下是隨時(shí)間變化的,即應(yīng)力與強(qiáng)度均應(yīng)為隨機(jī)過(guò)程。
2 動(dòng)態(tài)可靠性分析
2.1 隨機(jī)載荷的描述
Gamma過(guò)程增量具有非負(fù)的單調(diào)性,多用于描述不可逆轉(zhuǎn)的單調(diào)變化的隨機(jī)過(guò)程。在描述載荷、溫度、磨損、腐蝕等方面得到了廣泛應(yīng)用。在加速壽命試驗(yàn)中,為減少試驗(yàn)時(shí)間,常采用增加載荷的方法,Gamma過(guò)程在此類可靠性試驗(yàn)中也得到了廣泛運(yùn)用。
稱隨機(jī)過(guò)程{X(t),t≥0}服從形狀參數(shù)為a(t)、尺度參數(shù)為b的Gamma過(guò)程,如果其滿足下列條件:
(1)X(0)=0;
(2)X(t)在非相交的區(qū)間具有獨(dú)立增量X(t)-X(s)(t>s≥0);
(3)對(duì)任意t>s≥0,有增量X(t)-X(s)~Ga(a(t)-a(t),b)。
其中:Ga(·)表示Gamma分布,a(t)和b分別為形狀參數(shù)和尺度參數(shù),且a(t)為遞增的連續(xù)函數(shù),a(0)=0,b>0。當(dāng)a(t)為現(xiàn)象函數(shù)時(shí),Gamma過(guò)程為平穩(wěn)過(guò)程;當(dāng)a(t)為非線性函數(shù)時(shí),Gamma過(guò)程為非平穩(wěn)過(guò)程。設(shè)X(t)為零件t時(shí)刻承受的載荷,則其概率密度函數(shù)為:
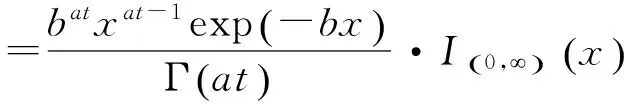
(3)
式中:Γ(·)表示Gamma函數(shù),即:
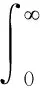
(4)
IA(x)為示性函數(shù);當(dāng)x∈A時(shí),有IA(x)=1,若x?A時(shí),有IA(x)=0。由平穩(wěn)增量的性質(zhì)可知,在任意時(shí)刻t,隨機(jī)過(guò)程X(t)的數(shù)學(xué)期望和方差將隨時(shí)間呈線性增長(zhǎng)的趨勢(shì),則有下列表達(dá)式:
μX(t)=at/b
(5)
(6)
2.2 隨機(jī)載荷下的強(qiáng)度退化模型
材料的疲勞性能通常用其承受的應(yīng)力s與失效時(shí)的應(yīng)力循環(huán)次數(shù)N之間的關(guān)系來(lái)描述,即經(jīng)典疲勞強(qiáng)度理論中的s-N曲線。在s-N曲線上,對(duì)應(yīng)于壽命N時(shí)的應(yīng)力值,稱為材料壽命為N時(shí)的疲勞強(qiáng)度。因此,s-N曲線也稱為疲勞強(qiáng)度-壽命曲線。s-N曲線反映的另一種信息是:隨著載荷作用次數(shù)的增加,材料強(qiáng)度在逐漸降低。
s-N曲線通常用冪函數(shù)表示,即零件疲勞性能曲線滿足下式[12]:
smN=C
(7)
式中:m、C為與材料性質(zhì)有關(guān)的常數(shù),N為載荷s作用下的零件壽命。
由式(6)可知,當(dāng)應(yīng)力s作用時(shí),零件的壽命為N。由Miner累積損傷理論,應(yīng)力s作用時(shí)對(duì)零件造成的損傷為1/N,即有1/N=sm/C。
假設(shè)零件在某隨機(jī)載荷s(t)作用下工作,則由式(6)可得到:
(8)
零件在經(jīng)時(shí)間t之后,其累積損傷D(t)為:
(9)
零件在下一時(shí)刻t+Δt載荷作用時(shí)不發(fā)生失效,則要求:
(10)
考慮零件的安全性,式(10)右端可設(shè)為一個(gè)小于1的數(shù),受多種因素的影響,該值實(shí)際上為分布在1附近的隨機(jī)變量。為簡(jiǎn)化討論,這里取為常數(shù)1。將式(8)代入式(9)并化簡(jiǎn)得:
(11)
所以,在經(jīng)歷載荷作用時(shí)間t之后,零件能夠抵抗的臨界載荷S(t)為:
(12)
在初始時(shí)刻,即t=0時(shí),由式(12)可知s(0)=C1/m。從廣義上來(lái)說(shuō),臨界載荷可以稱為強(qiáng)度。式(11)即是隨機(jī)載荷下的剩余強(qiáng)度模型,該式表明,隨著載荷作用時(shí)間的增加,零件強(qiáng)度逐漸降低,也就表現(xiàn)了載荷與強(qiáng)度之間的單向相關(guān)性。
3 單向相關(guān)下的動(dòng)態(tài)可靠性模型
早期對(duì)可靠度的計(jì)算多采用強(qiáng)度與應(yīng)力相獨(dú)立的假設(shè),以此得到的結(jié)果與工程實(shí)際有一定的偏差。實(shí)際上在應(yīng)力作用的過(guò)程中,強(qiáng)度通常會(huì)逐漸降低,即強(qiáng)度與應(yīng)力是相關(guān)的。這與事實(shí)相符合,也得到了大量實(shí)驗(yàn)的驗(yàn)證。零部件的強(qiáng)度往往受到應(yīng)力的影響,在不同的應(yīng)力條件下表現(xiàn)出不同的特性,而應(yīng)力則取決于載荷、工況等外部環(huán)境,與強(qiáng)度無(wú)關(guān)。因此,強(qiáng)度與應(yīng)力表現(xiàn)為一種單向相關(guān)的現(xiàn)象。
上文利用Gamma過(guò)程對(duì)隨機(jī)載荷進(jìn)行了描述,并由Miner損傷累積建立了隨機(jī)載荷下的零件強(qiáng)度退化模型。根據(jù)應(yīng)力-強(qiáng)度干涉模型,零件在任意時(shí)刻的動(dòng)態(tài)可靠度函數(shù)可以表示為:
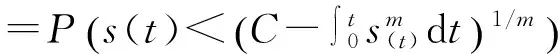
(13)
式(13)即為應(yīng)力與強(qiáng)度單向相關(guān)下的零件動(dòng)態(tài)可靠度模型。
4 算例分析
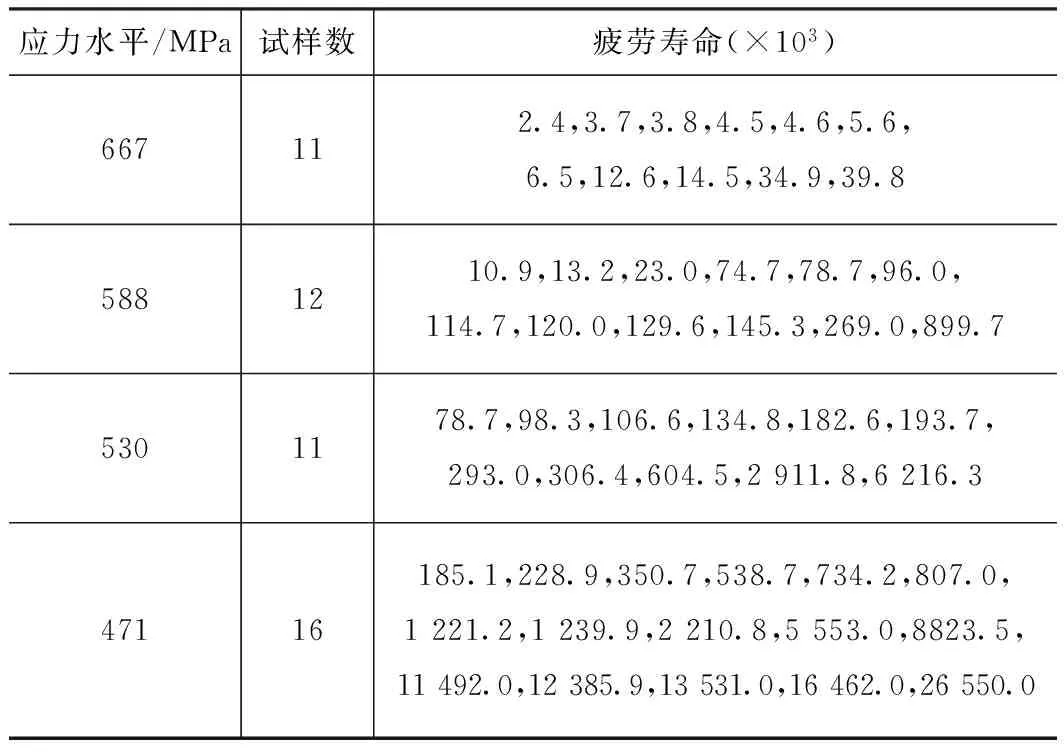
為對(duì)本文方法的有效性進(jìn)行驗(yàn)證,在此以文獻(xiàn)[13]中提供的風(fēng)電葉片復(fù)合材料疲勞試驗(yàn)數(shù)據(jù)為例。試樣材料為單向碳/環(huán)氧復(fù)合材料,在瑞士產(chǎn)AMSLER 10HFP1-478高頻疲勞試驗(yàn)機(jī)上進(jìn)行軸向拉-拉加載疲勞試驗(yàn),疲勞試驗(yàn)數(shù)據(jù)如表1所示。
表1 疲勞試驗(yàn)數(shù)據(jù)
應(yīng)力水平/MPa試樣數(shù)疲勞壽命(×103)667112.4,3.7,3.8,4.5,4.6,5.6,6.5,12.6,14.5,34.9,39.85881210.9,13.2,23.0,74.7,78.7,96.0,114.7,120.0,129.6,145.3,269.0,899.75301178.7,98.3,106.6,134.8,182.6,193.7,293.0,306.4,604.5,2911.8,6216.347116185.1,228.9,350.7,538.7,734.2,807.0,1221.2,1239.9,2210.8,5553.0,8823.5,11492.0,12385.9,13531.0,16462.0,26550.0
根據(jù)表1中的試驗(yàn)數(shù)據(jù)(第一列與第三列),利用最小二乘法,對(duì)式(7)中的未知參數(shù)進(jìn)行估計(jì),得m=17.999 9,C=9.675 2×1054。則單向碳/環(huán)氧復(fù)合材料試樣的s-N曲線的方程式為:
s17.999 9N=9.675 2×1054
(14)
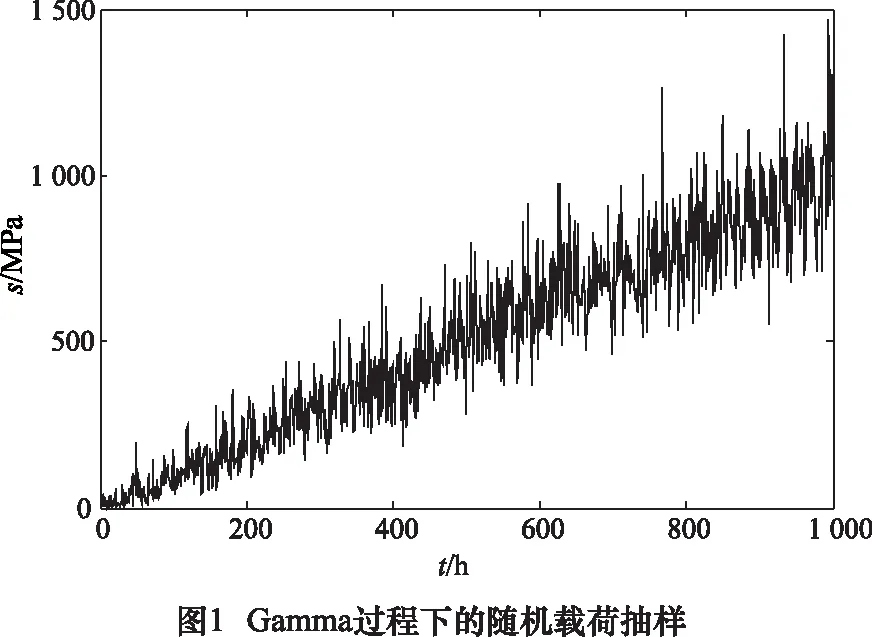
零件在隨機(jī)載荷作用下工作,載荷加載過(guò)程用平穩(wěn)的Gamma過(guò)程描述,a=0.05,b=20。對(duì)隨機(jī)載荷進(jìn)行抽樣分析,仿真結(jié)果如圖1所示。對(duì)零件的可靠度進(jìn)行Monte Carlo仿真,運(yùn)用式(13)可得零件的可靠度變化曲線如圖2所示。由圖2可知,零件的可靠度曲線隨著時(shí)間的增加具有明顯下降的趨勢(shì),在t=630 h之前,零件能保持穩(wěn)定工作,之后零件的可靠度迅速降低,并最終不能滿足工作需求而發(fā)生失效。
5 結(jié)語(yǔ)
本文利用Gamma過(guò)程來(lái)描述隨機(jī)載荷作用,基于經(jīng)典的Miner累積損傷理論,推導(dǎo)了隨著載荷作用而產(chǎn)生的強(qiáng)度不斷降低的強(qiáng)度退化模型。結(jié)合傳統(tǒng)的應(yīng)力-強(qiáng)度干涉模型,提出了一種基于隨機(jī)過(guò)程的應(yīng)力-強(qiáng)度單向相關(guān)下的零件動(dòng)態(tài)可靠度分析方法,并建立了相應(yīng)的可靠度模型。通過(guò)算例驗(yàn)證了模型的有效性。算例結(jié)果表明:該模型能夠有效用于可靠性分析,具有一定的工程指導(dǎo)意義。
[1]張義民. 機(jī)械動(dòng)態(tài)與漸變可靠性理論與技術(shù)評(píng)述[J]. 機(jī)械工程學(xué)報(bào), 2013, 49(20): 101-108.
[2]王正, 康銳, 謝里陽(yáng). 隨機(jī)載荷多次作用下的零件失效率計(jì)算模型[J]. 北京航空航天大學(xué)學(xué)報(bào), 2009, 35(4): 407-410.
[3]王正, 謝里陽(yáng). 不確定性載荷作用下的零件時(shí)變可靠性模型[J]. 航空學(xué)報(bào), 2009, 30(7): 1243-1247.
[4]左勇志, 劉西拉. 結(jié)構(gòu)動(dòng)態(tài)可靠性的全隨機(jī)過(guò)程模型[J]. 清華大學(xué)學(xué)報(bào), 2004, 44(3): 395-397.
[5]孫權(quán), 趙建印, 周經(jīng)綸. 復(fù)合應(yīng)力作用下強(qiáng)度退化的應(yīng)力-強(qiáng)度干涉模型可靠性統(tǒng)計(jì)分析[J]. 計(jì)算力學(xué)學(xué)報(bào), 2007, 24(3): 358-361.
[6]方永鋒, 陳建軍, 馬洪波. 共同隨機(jī)載荷下結(jié)構(gòu)動(dòng)態(tài)可靠性分析[J]. 應(yīng)用力學(xué)學(xué)報(bào), 2016(2): 345-351.
[7]方永鋒, 陳建軍, 馬洪波. 多種隨機(jī)載荷下的結(jié)構(gòu)動(dòng)態(tài)可靠性計(jì)算[J]. 振動(dòng)與沖擊, 2013, 32(1): 118-121.
[8]王新剛, 張義民, 王寶艷. 機(jī)械零部件的動(dòng)態(tài)可靠性靈敏度分析[J]. 機(jī)械工程學(xué)報(bào), 2010, 46(10): 188-193.
[9]高鵬, 謝里陽(yáng). 基于相關(guān)性分析的載荷-強(qiáng)度干涉模型[J]. 東北大學(xué)學(xué)報(bào), 2010, 31(12): 1753-1756.
[10]Schaff J R, Davidson B D. Life prediction methodology for composite structures[J]. Journal of Composite Materials, 1997, 31(2): 128-157.
[11]謝里陽(yáng), 王正, 周金宇,等. 機(jī)械可靠性基本理論與方法[M]. 北京: 科學(xué)出版社, 2009: 77-79.
[12]楊智, 王術(shù)新, 董華玉, 等. 載荷-強(qiáng)度相關(guān)的機(jī)械零件動(dòng)態(tài)可靠性分析[J]. 裝甲兵工程學(xué)院學(xué)報(bào), 2014, 28(2): 17-19.
[13]徐人平, 詹肇麟, 段小建. 復(fù)合材料疲勞壽命數(shù)據(jù)研究[J]. 材料開(kāi)發(fā)與應(yīng)用, 1994, 9(4): 18-21.

