基于SDG-QTA的一回路冷卻劑系統故障診斷方法研究?

楊 光 鐘小軍

1 引言

一回路冷卻劑系統作為防止裂變產物外泄的第二道屏障，可以保證堆芯的熱量及時散出，防止對堆芯熔毀。要保證核電廠的正常運行，就要時刻保障冷卻劑系統正常而高效的運行。所以，及時發現故障源并進行處理就變得非常重要［1～2］。

SDG通過定性因果模型將龐大的系統變量的邏輯關系用有向圖的形式呈現出來［3］。然而傳統的SDG診斷方法雖能快速發現故障源，并可以將傳播路徑完整的展現出來，但各個節點只能表示當前時刻的狀態，即只能在“+”“-”或“0”三中選一［4］。SDG針對多故障同時發生的情況，辨別能力不強。尤其在故障數據沒超過設定閾值的這段時間，SDG不能在核設備出現故障時進行診斷，因而造成不能及早發現故障的后果。利用QTA靈敏度高、隔離性好、算法復雜程度小的特點將SDG的種種不足加以彌補［5］。

所以，將SDG和QTA應用于一回路冷卻劑系統早期診斷。在數據還在五級閾值內，但已超過三級閾值時，通過提取數據的定性趨勢來判斷數據是否有超過五級閾值的可能，盡可能在早期確定系統發生的故障。再通過基于節點的融合了SDG和QTA的相容規則反向推理，找到疑似的故障源及其傳播路徑。按著對疑似的故障源及傳播路徑計算可信度系數排序，最終確定全部真實的故障源［6］。這樣就可以幫助控制臺操作人員分析故障，輔助決策，提供準確、及時的服務，減輕操作人員的工作壓力。

2 基于SDG-QTA的故障分析方法

傳統SDG應用在核動力裝置中變量之間關系繁雜，核電廠防護系統眾多，對節點參數值調整幅度、頻率不同，導致節點狀態不定，容易漏掉真正的故障。閾值設定不準確，傳感器容易造成誤差，也會造成漏掉真正故障。

當出現有效節點一定時間，以SDG模型為基礎進行，采用此框架進行分析。

2.1 框架中的基本概念

定義1：敏感閾值 為了實現故障早期發現，選擇比工作閾值更加敏感的閾值范圍作為敏感閾值。敏感閾值能有效地提高監測的靈敏度，并運用QTA方法減小故障誤報的可能性。

定義2：工作閾值 在工程應用中，大部分需監測的變量都擁有自身閾值，稱為工作閾值。目的就是保證參數限制在正常范圍，系統能正常運行［7］。而為了使系統正常運行，但盡量又不觸發誤報，一般各個工作閾值范圍偏大，不利于故障早期發現。

定義3：SDG-QTA有效節點規則 SDG-QTA

有效節點規則決策樹，如圖1。

圖1 SDG-QTA有效節點決策樹

2.2 閾值的選取方法

1）U檢驗

在核電廠正常工作時，其運行的數據會出現隨機波動，可以使大部分參數的數據服從正態分布［8～9］。閾值的選取規則如圖2。

圖2 閾值的選取規則

為了能更加了解參數在時間上的分布，我們用U檢驗來校核其是否服從正態分布。

2）敏感閾值的選取

進行U檢驗后，若參數符合正態分布，則通過該分布選取敏感閾值。若參數不服從正態分布時，則選取參數中的最大值和最小值作為工作閾值上下限值。

正態分布中當參數X＜3σ時（σ為標準差），發生概率為0.9987，若參數變化服從正態分布，可以分析正常運行的參數確定工作閾值。正常運行時參數的絕對值小于3σ發生的概率是0.0026，若連續3s均發生這種情況，其概率為0.00263=1.76×10-8，發生概率非常低。選取3σ為敏感節點，參數連續3s均在閾值外，則認為該參數可能出現異常。

2.3 診斷框架整體步驟

整體的診斷框架如圖3所示。

1）檢測節點參數，判斷是否超出敏感閾值。

2）檢測出超出敏感閾值，用QTA中趨勢識別提取，擬合出該節點一段時間后的趨勢。按照發生SDG-QTA故障規則，考慮早期故障階段，該節點是否為有效節點。

3）針對有效節點進行實時QTA，識別提取趨勢。

4）根據SDG模型的推導與診斷方法，進行正向推理與反向推理，盡可能找出全部相容路徑和候選故障源。計算可信度系數，從高到底的順序進行排序［10］。

5）找出故障源。

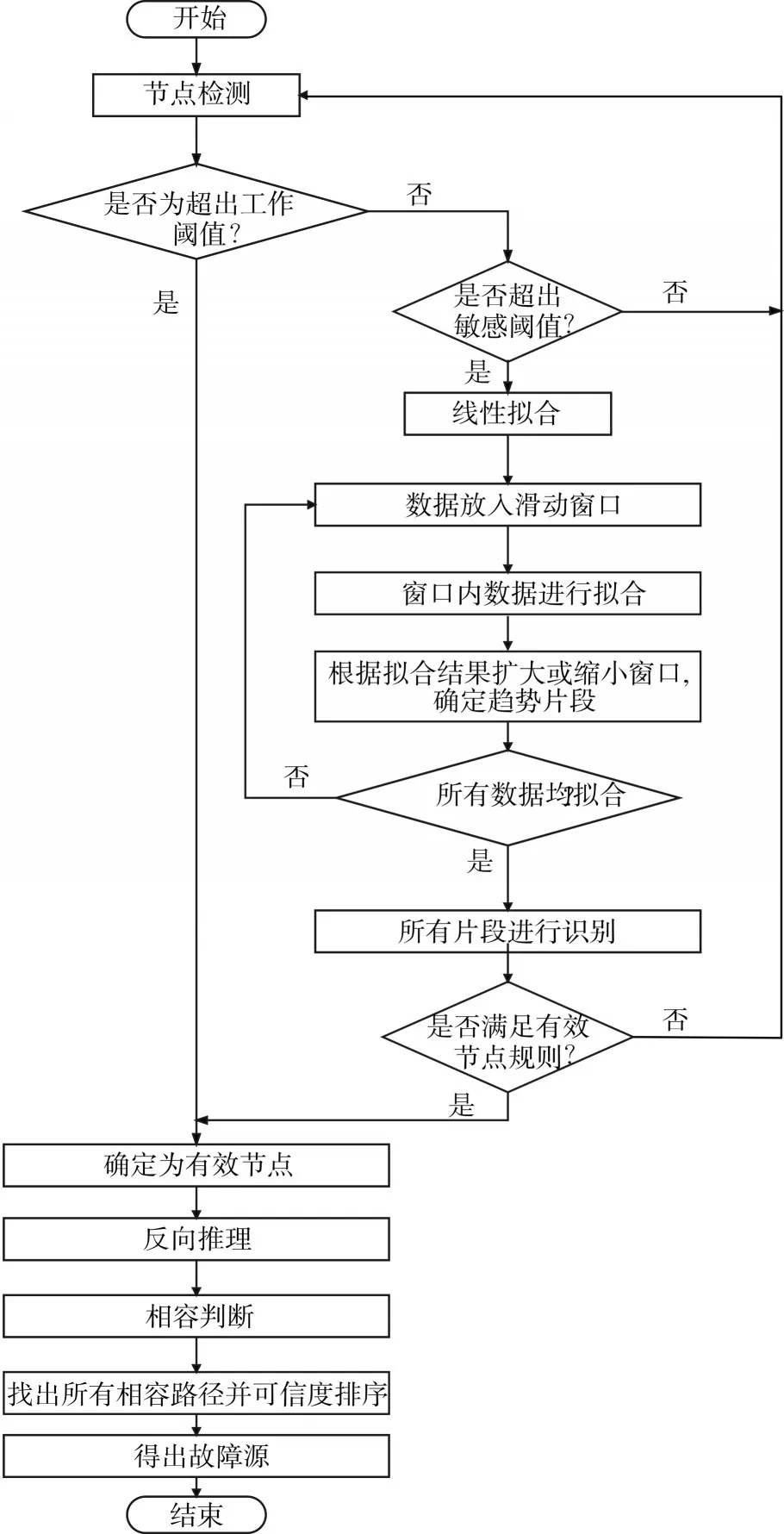
圖3 SDG-QTA方法診斷流程圖

3 QTA趨勢識別提取方法

本論文采用Sylvie Charbonnier等提出的語言來描述趨勢［11］。這種語言定義了三個基元，如圖4。

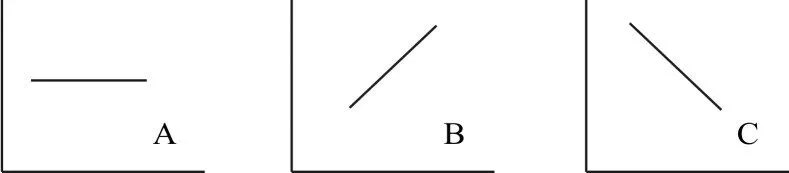
圖4 基本趨勢基元

A狀態代表節點未發生變化；B狀態代表節點有上升趨勢；C狀態代表節點有下降趨勢。采用三基元表示可以在滿足趨勢識別需要的同時，降低系統復雜度，達到更加快速識別的目的。

趨勢識別提取的算法首先用最小二乘法擬合，得到線性片段。但最小二乘法的使用事先不知道并變量與時間的線性關系，所以對所得的擬合結果進行F檢驗，驗證所得的結果。

4 SDG和QTA結合的反向推理

4.1 推理過程中的相容規則

1）支路狀態為正，節點對應的趨勢片段應一致才相容，即都為“上升”或“下降”。

2）支路狀態為負，節點對應的趨勢片段應相反才相容，即一個為“上升”，另一個為“下降”。

3）普通節點與故障源一定為相容的。

若同一支路的兩端節點，一個基元為A，另一基元為B或C，則為半相容。

4.2 反向推理主要算法

1）以已知的有效節點作為初始起點，反向搜索上層待探索節點。

2）按相容規則判斷含有定性趨勢片段的兩節點是否相容。

3）若相容，上層節點作為起點，再次進行2），直至找到終節點，即非原因節點且無上層節點的節點。

4）若不相容，找其他能相容的上層節點。若沒有，返回上個節點，作為當前節點，直至回到初始起點。

5）繼續從初始起點出發，重復以上步驟，至初始起點再無相容節點。

6）探索所有的有效節點后，結束。

4.3 可信度系數計算并排序

可信度系數（C.I.）體現了相容路徑成為故障傳播路徑的可能性，值越高，成為真正故障傳播路徑的可能越高。

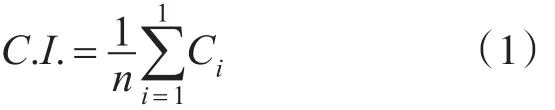
n為整個相容路徑的支路數，Ci為支路i的可信度。

Si為每個基元相容的權值。若兩個片段相容，則 Sj為1；半相容，則 Sj為0.5。

式（1）、（2）說明，兩個節點趨勢識別出的片段相容的越多，相容的可能性越大，故障沿此相容路徑傳播的可能性越大。通過對每個相容路徑計算可信度系數，根據C.I.進行排序，可以大幅提高診斷的分辨率。

5 SDG-QTA方法的應用

本文以冷卻劑喪失事故為例，對SDG-QTA方法的診斷推理過程進行分析。冷卻劑喪失事故是指反應堆一回路壓力邊界不再完整，產生破口，一定量冷卻劑從破口泄出的事故，簡稱LOCA（Loss of Coolant Accident）［12］。冷卻劑喪失事故造成的后果，由于事故現象復雜、情況多樣，變得非常嚴重。因此，該故障在安全分析中處于重要地位。由于冷卻劑大量喪失，導致堆芯冷卻能力不足，熱量不能及時導出。嚴重情況下會導致堆芯熔毀［13］。

LOCA→環路冷卻劑壓力→主冷卻劑系統平均壓力→穩壓器壓力→穩壓器水位；LOCA→環路冷卻劑流量→蒸汽發生器水位→蒸汽發生器蒸汽流量→蒸汽發生器壓力→蒸汽管道壓力；LOCA→安全殼放射性；LOCA→地坑水位；LOCA→安全殼內壓力；LOCA→安全殼內溫度。

簡化后的SDG模型，如圖5所示。

圖5 LOCA的SDG模型

水位的趨勢基元為C；蒸汽發生器水位的趨勢基元 為C；蒸汽管道壓力的趨勢基元為C；蒸汽發生器壓

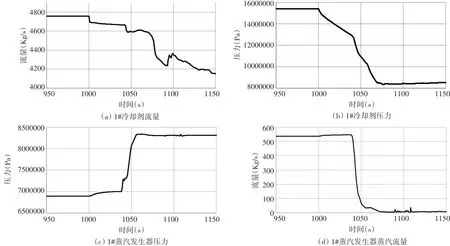
圖6 故障發生后的各節點參數值

而在故障于第1000s發生之后，變量的數據如圖6所示。

在采樣時間為50s的早期故障中，1#冷卻劑流量、1#蒸汽發生器壓力節點參數值未超過工作閾值，但超過敏感閾值。用未結合QTA的SDG方法進行故障診斷，結果為未發現故障。而運用SDG-QTA方法能判斷出，該節點為有效節點，該路徑疑似故障路徑。1#冷卻劑壓力的趨勢基元為C；1#冷卻劑流量的趨勢基元為A；一回路平均壓力的趨勢基元為C；穩壓器壓力的趨勢基元為C；穩壓器力的趨勢基元為B；1#蒸汽發生器蒸汽流量的趨勢基元為C。

LOCA→環路冷卻劑壓力→主冷卻劑系統平均壓力→穩壓器壓力→穩壓器水位。

計算得到該條相容通路的可信度：

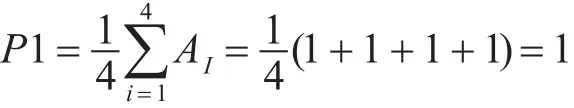
LOCA→環路冷卻劑流量→蒸汽發生器水位→蒸汽發生器蒸汽流量→蒸汽發生器壓力→蒸汽管道壓力。

計算得到該條相容通路的可信度

在發生故障100S以后，1環路冷卻劑流量的趨勢基元變為C；蒸汽發生器壓力的趨勢基元變為A，其余的節點趨勢基元均為A，即不變。

LOCA→環路冷卻劑壓力→主冷卻劑系統平均壓力→穩壓器壓力→穩壓器水位。

計算得到該條相容通路的可信度：

LOCA→環路冷卻劑流量→蒸汽發生器水位→蒸汽發生器蒸汽流量→蒸汽發生器壓力→蒸汽管道壓力。

計算得到該路徑的可信度系數：

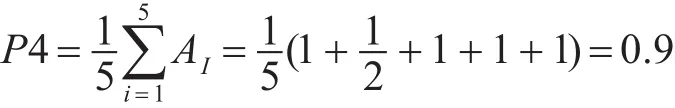
最終能確認兩條路徑均為故障路徑，并且其他路徑的分析同理，從而確定故障源為LOCA。

6 結語

1）SDG-QTA建立模型方法能診斷出核電廠設備的故障。建立一回路系統的LOCA的SDG模型，利用SDG-QTA進行診斷，取得了良好的故障診斷效果。

2）通過合理的簡化提高模型分析效率和準確性。在典型故障SDG模型簡化過程中，簡化掉不可測量的節點和弱關聯支路，降低了復雜程度，而模型的正確性未受到影響。

［1］鄭福裕，邵向業，丁云峰.核電廠運行概論［M］.北京：原子能出版社，2010.

［2］MAURYA M R，RENGASWAMY R，VENKATASUBRA?MANIAN V.Application of signed digraphs-based analy?sis for fault diagnosis of chemical process flowsheets［J］.Engineering Applications Artificial Intelligence，2004，17（5）：501-518.

［3］高東，許欣，馬昕.基于SDG與趨勢分析的故障診斷框架［J］. 計算機工程與應用.2014（13）：6-9.

［4］黃衛東，王克昌.基于定性和定量關系的液體火箭發動機故障診斷［J］.航空動力學報，1996，11（3）：281-284.

［5］吳軍強，梁軍.基于圖論的故障診斷技術及其發展［J］.機電工程，2003，20（5）：188-190.

［6］劉敏華，蕭德云.基于趨勢分析和SDG模型的故障診斷［J］. 控制理論與應用.2006（02）：306-310.

［7］曹文亮.基于SDG的熱力系統故障診斷方法研究［D］.北京：華北電力大學（河北），2006.

［8］李安峰，夏濤，張貝克，等.化工過程SDG建模方法［J］.系統仿真學報.2003，15（10）：1364-1368.

［9］李秀喜，吉世明.基于半定量SDG模型的化工過程故障診斷［J］.清華大學學報：自然科學版，2012，52（8）：1112-1115.

［10］Charbonnier S，Garcia-Beltan C，Cadet C，et al.Trends extraction and analysis for complex system monitoring and decision support［J］.ENGINEERING APPLICA?TIONS OF ARTIFICIAL INTELLIGENCE.2005，18（1）：21-36.

［11］Wen-Liang C，Bing-Shu W，Liang-Yu M，et al.Study of fault diagnosis approach based on rules of deep knowl?edge representation of signed directed graph［C］//Hong Kong：2005.

［12］朱繼洲.核反應堆安全分析［M］.西安：西安交通大學出版社，2004.

［13］ZHANG Zhaoqian，WU Chongguang，ZHANG Beike，et al.SDG multiple fault diagnosis by real-time inverse in?ference［J］.Reliability Engineering and System Safety，2005，87：173-189.