判斷折線自相交的完備算法與快速顯示技術

魏志云 王國光 李成翔

摘要：折線自相交是地理信息系統（Geographic Information System，簡稱GIS）空間線性數據檢查處理中的一個重要問題，如何快速判斷、準確定位是這個問題的關鍵。在對MicroStation API熟練掌握并運用的基礎上，對折線自相交中存在交叉、重復、重疊的情況進行全面分析，解決了API開發庫函數無法對線段重疊情況下的相交判斷問題，并最終實現求交結果的預覽和快速顯示功能，極大方便用戶快捷、準確地辨識折線自相交的類型和位置。

關鍵詞：GIS；MicroStation；自相交；快速顯示

中圖分類號：TP311 文獻標識碼：A 文章編號：1009-3044（2018）06-0229-03

在地理信息數據質量控制中，折線自相交是影響線型數據質量的關鍵因素，在地圖綜合、空間分析等領域有著廣泛的應用。例如，地圖上的等高線、水系、境界等線狀要素的綜合，要求同代表某一要素的折線自身不能相交。但是由于地圖上的曲線具有復雜、多樣和密集等特點，運用一定的算法化簡后不可避免地產生自相交，因此需要設計一套合適的算法來消除這種現象。

近年來，國內外學者在判斷折線自相交方面開展了一些工作，但都存在效率不高的問題。MicroStation是一款三維CAD設計軟件，具有強大的API開發庫函數，為該軟件的二次開發提供了很好的接口。目前該軟件庫函數對于線段內部相交的情況有較好的解決，而對于線段重疊的情況則沒有考慮，因此設計一套完備的求交算法，彌補線段求交的不足顯得非常必要。

本文利用MicroStation API開發庫函數求解一般情況下的折線自相交，詳細分析了折線自相交在重復、重疊情況下的自相交，全面而又準確地判斷出折線自相交的類型和位置，為用戶快速判斷折線自相交提供了一種可靠方法。

1折線自相交判斷相關定義

1.1折線自相交的定義

設有折線L={p₁，…p_i，…p_n}，（i=1，2，…，n），p_i是折線上順次相連線段的端點。若除了相鄰線段間的連接端點p₁，p₂，…，p_n外，折線上的線段之間還存在其他的交點，則定義此折線為自相交折線。

1.2判斷折線自相交的一般算法

判斷折線自相交一般采用如下算法：對于折線三上的線段，按照其連接順序分解為n-1條兩點組成的線段，然后兩兩判斷這些線條之間是否相交，根據交點情況和自相交的定義來判斷折線L是否自相交。該算法很成熟，在相關論文中已經有介紹，在此不予給出。

折線自相交的一般算法對于線段內部相交適用，但對于線段重疊情況下的相交無法判斷，如完全重疊、部分重疊等。本文在MicroStation已有函數的基礎上，補充折線自相交在重疊情況下的判斷，完善了折線自相交的全部情況。

1.3折線自相交的分類

為了更好的說明問題，將自相交分為：重點式自相交、交叉式自相交、重疊式自相交三種情況，相交結果分成重復點、交點＼重疊點、重疊線三類。

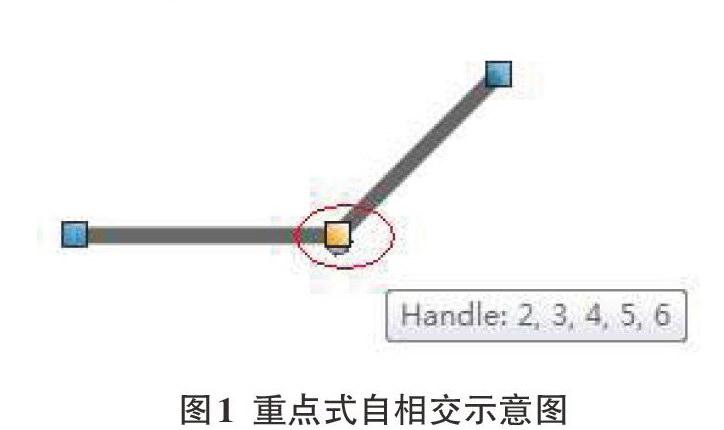
（1）重點式自相交判斷

重點式自相交是折線中連續兩個或者多個頂點出現在同一位置，也即折線中存在長度為零的線段，它是折線自相交中一種常見類型。在繪制地圖線性要素的時候，難免會出現重復點現象，如圖1所示。

對折線中重復點進行排除算法比較簡單，只需要比較當前點與下一個節點坐標是否相等即可，若該點與下一頂點坐標一樣，則判斷該點為重復點，并將下一頂點刪除，依此循環判斷。

（2）交叉式自相交判斷

交叉式自相交是折線中不平行線段之間產生交點，包括內部點和端點，它是折線自相交的一種普遍類型。交叉式自相交判斷用到MicorStation API中三維線段求交函數mdlVec_inter-sectXYZLines，該函數需要分別輸入兩條線段的首尾端點坐標以及容差，輸出交點坐標、交點分別在兩條線段中的比例參數paramAP和paramBP。

根據比例參數paramAP、paramBP，在排除外部相交的情況下，可將交叉式自相交分為如下4類。

（3）重疊式自相交判斷

為了加快判斷速度，在判斷重疊式自相交之前，增加兩線段是否平行的判斷，這里用到MicroStation API中向量平行測試函數mdlVec_areParallel。

重疊式自相交是折線中平行線段間的重疊，包括重疊點和重疊線，它是折線自相交的一種特殊類型。重疊點是指兩線段中某一端點坐標相同；重疊線是指兩線段中某一段坐標相同。為了全面分析相交的情況，本文采取端點距離判斷法，實現重疊式自相交的判斷，其算法思想如下：

2）一端點重合

如果端點距離Dist（i，j）、Dist（i，j+1）、Dist（i+1，j）、Dist（i+1，j+1）中僅有一個為零，則判斷為一端點重合，相交結果為重疊點或重疊線。首先將其分為如下4大類，然后每大類又可分成3種具體情況，需要根據其余四個距離之間的關系進一步判斷相交結果，其示意圖解如表3。

3）無端點重合

如果端點距離Dist（i，j）、Dist（i，j+1）、Dist（i+1，j）、Dist（i+1，j+1）都不為零，則判斷為無端點重合，相交結果要么是部分重合，也即相交結果為重疊線，要么不相交。本文對于部分重合的情況羅列如下。

2判斷折線自相交的完備算法

基于以上對折線自相交判斷的詳細分類和求解方法介紹，研究出一套完整的折線自相交判斷算法，該算法基本步驟如下。

第一步：設折線選擇集LS的個數為m，遍歷LS，獲取折線LS（i）的坐標信息，其中i=0，1，…，m-1；

第二步：首先對折線LS（i）進行重點式自相交判斷，若有重復點，則將重復點添加到相交集合中，并將該重復點從折線點集中刪去。

第三步，設折線LS（i）上點的個數為n，則將折線看成n-1條依次相連的線段構成，判斷折線自相交即可分解為判斷這n-1條線段兩兩之間是否相交。將第i條線段記為L（j），其中j=0，1，…，n-3；其后的n-j-1條線段中的一段記為L（k），其中k=j+1，…，n-2。第{條都要與其后的n-j-1條線段進行求交計算，時間復雜度為O（n²）。

第四步：判斷線段L（j）與線段L（k）矩形外包是否有交集，若有交集，則跳到第五步，否則返回到第三步進行下一對線段的相交判斷；

第五步：應用MicroStation自帶三維求交函數mdlVec_inter-sectXYZLines進行求交計算，若求交成功，則根據比例參數進一步判斷是否交叉式自相交，若是交叉式自相交則求出交點，并將交點添加到相交集合中，返回到第三步進行下一對線段的相交判斷；若不成功，則跳到第六步。

第六步：應用MicroStation自帶向量平行測試函數mdlVec_areParallel判斷兩條線段是否平行，若平行，則進行重疊式自相交判斷，并求出重疊點或重疊線的坐標，并將相交結果添加到相交集合中，最后返回到第三步進行下一對線段的相交判斷。

根據以上步驟，其算法流程圖如圖4所示。

3計算結果的預覽和快速顯示

為了讓用戶更加方便地了解相交的位置和類型，本算法增加了相交結果的預覽和陜速高亮顯示功能。

相交結果預覽采取序號和相交類型組成，相交類型可分為三種：交點/重疊點、重疊線、重復點，分別用0、1、2及以上表示，其對應關系如表4所示。

在MicroStation中，開發者可以通過繪制臨時元素和臨時幾何圖形兩種方式實現相交結果的高亮顯示。二者的區別在于MicroStation Development Library（MDL）函數只能創建一個普通的元素，然后將該元素轉化為臨時元素，當視圖變化、元素較多時，臨時元素會不斷地被創建，占用較大內存，顯示延遲；而通過MicroStation API中的IviewTransients接口可以定義任意幾何形狀，無需創建元素，能更方便快速地控制其在視圖更新過程中的顯示。

顯然，用戶期望知道相交結果的位置，然后手動修改，而不希望該相交結果變成臨時元素被不斷添加到視圖中，影響效率。因此，本文采取第二種方法，通過IviewTransients接口生成臨時幾何圖形，用戶可以通過雙擊預覽數據列表行，精確定位該相交位置。

從圖5、圖6測試實例中我們可以得出，根據以上算法求解的自相交情況與實際情況相當吻合，用戶可以掌握全部自相交的數據，并能快速定位，提高了查找效率，為用戶進一步調整提供了很大的方便。

4結束語

本文在MicroStation API的基礎上，對折線自相交進行了詳細分類，。考慮了折線自相交會出現的所有情況，采用距離判斷法解決折線某段重合下的自相交，從而設計出判斷折線自相交的完備算法。由于在進行自相交計算之前需要通過矩形外包交集測試，因此該算法能快速判斷線性元素是否自相交。

利用IviewTransients接口實現相交結果的快速顯示，對于海量數據自相交結果的顯示，其優越性更加明顯。該算法提高了數據處理效率和數據的準確性，便于用戶準確定位并進行手動調整，具有實現簡單、檢查全面、易于查找、穩定性好等特點。