FIR數字濾波器的設計與研究
王 輝
(海裝重慶局,重慶 400030)
0 引言
有限沖擊響應(FIR)數字濾波器具有嚴格的線性相位和任意幅度的特性,并且其單位抽樣響應是有限長序列,濾波器極其穩定,因此廣泛應用于圖像處理及數據傳輸中。而FPGA具有靈活的可編程邏輯,并且突破了并行處理與流水級數的限制,具有速度快、功耗低、可靠性高和可移植性高等特點。利用IP Core設計FIR濾波器,設計周期短,占用邏輯資源少,運算速度有大幅提高[1],故使用IP Core已逐漸成為數字信號處理的一種方式。本文采用數字仿真方式驗證了系統的正確性和有效性。
1 系統總體設計
整個系統由A/D采樣電路、FIR濾波器以及D/A轉換電路組成。為便于分析系統性能,對一特定的帶阻網絡進行了測量。A/D轉換電路用于采集經過帶阻網絡衰減后的信號,FIR濾波器對采集到的數據進行濾波,最后通過D/A轉換電路輸出處理后的波形。系統框圖如圖1所示。
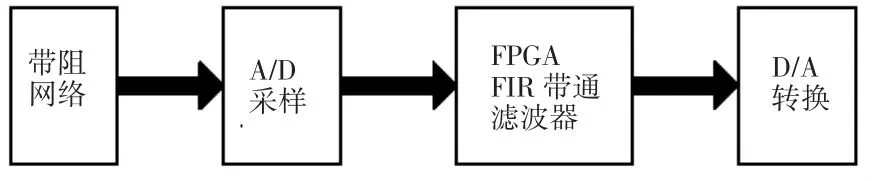
圖1 系統框圖
在本設計中,對帶阻網絡的幅頻特性進行測量,得出所需FIR濾波器的頻率響應。根據FIR濾波器的頻率響應特性,利用Matlab計算出濾波器的系數。并可通過Matlab仿真,驗證所設計的系統是否符合要求。最后將驗證過的數據導入IP核,即通過FPGA硬件實現所需要產生的濾波器。
2 FIR濾波器的設計
2.1 Matlab函數的設計
Matlab中提供的函數fir2是基于頻率取樣的FIR濾波器設計方法,其濾波器的頻率特性由頻率向量f和幅值向量a決定[2]。其基本的調用形式為:

式中,返回的行向量b是一個包含n+1個n階FIR數字濾波器的系數,此FIR濾波器的頻率特性是由f和a決定的。因此,只需要知道幅值與頻率的關系,就可計算出任意FIR濾波器的系數。
在本設計中,是通過已知的帶阻濾波器的幅頻特性來設計一個FIR帶通濾波器,要實現數字幅頻均衡,則需要滿足

式中,H1(jω)為帶阻網絡的幅頻響應,H2(jω)為FIR帶通網絡的幅頻響應[3]。式(2)表明,帶通濾波器的幅度值實際上可認為是帶阻網絡的幅度值的倒數。由帶阻網絡的幅頻特性,便可推算出需要產生的FIR帶通濾波器的性能指標。
經實際測量,帶阻網絡的中心頻率f0為3.7 kHz,其通頻帶BW=f2-f1=3 950 Hz-3 510 Hz=440 Hz.根據帶阻網絡的幅值取倒得到的FIR帶通濾波器的幅頻特性曲線如圖2所示。
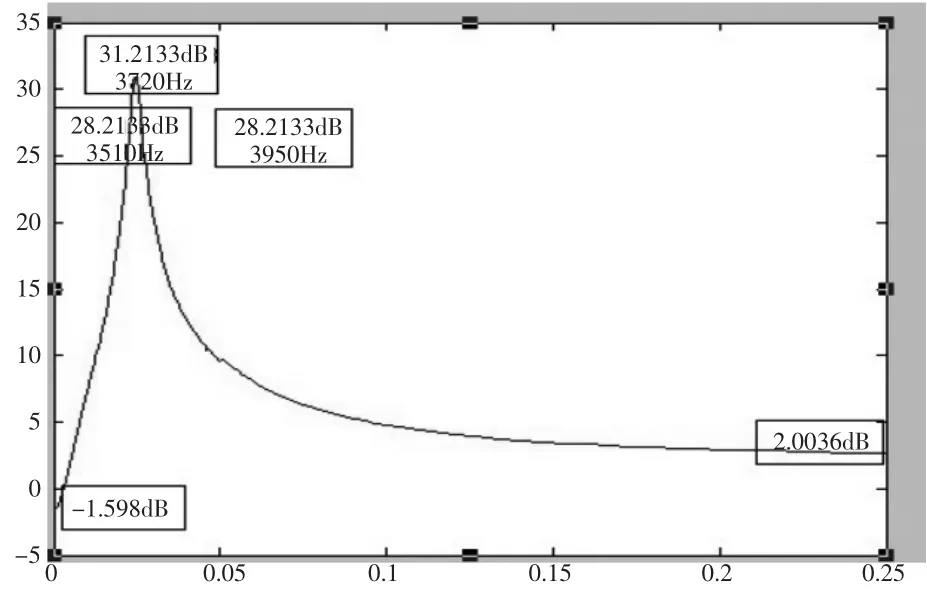
圖2 FIR濾波器頻率特性曲線
2.2 階數分析
調用函數fir2()算出300階時FIR帶通濾波器的系數[4],并由用可視化工具fvtool生成的幅頻特性曲線如圖3所示。
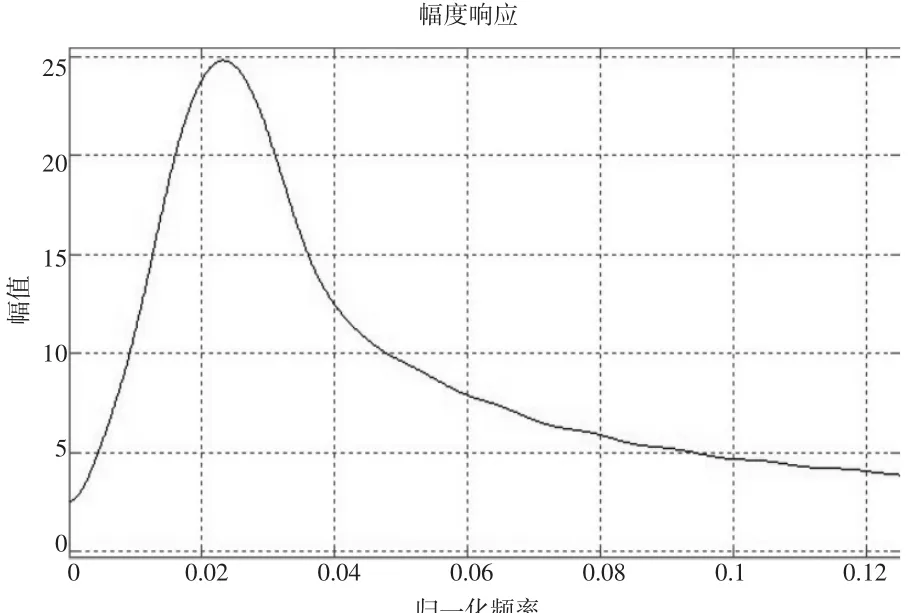
圖3300 階系數的頻率特性圖
比較圖2和圖3可以知道,處理后波形的幅頻特性圖與需要產生的幅頻特性圖大致相似,但圖3的衰減特性還不是很符合要求。將階數設置為2000時,其頻率特性圖如圖4所示。
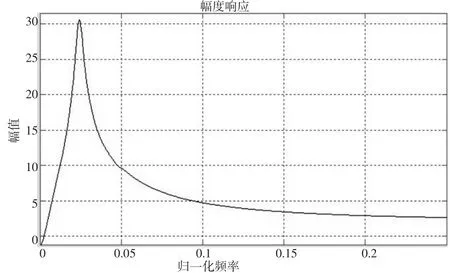
圖42000 階系數的幅頻特性圖
3 系統測試
3.1 不同階數的比較
保持采樣數據的個數不變,只改變FIR帶通濾波器的階數,實際測試的數據如表1所示。

表1 實際幅頻特性與階數的關系
由表1可知,設置的濾波器階數越高,其通頻帶越小,衰減特性也越陡峭,也越接近需要設計的FIR帶通濾波器。
3.2 資源利用率
而FPGA資源利用率與FIR濾波器階數近似成正比的關系,因此無限地提高濾波器的階數的同時,也會大大增加系統的資源損耗[5]。經實際測量,資源利用率與階數的關系如表2所示。
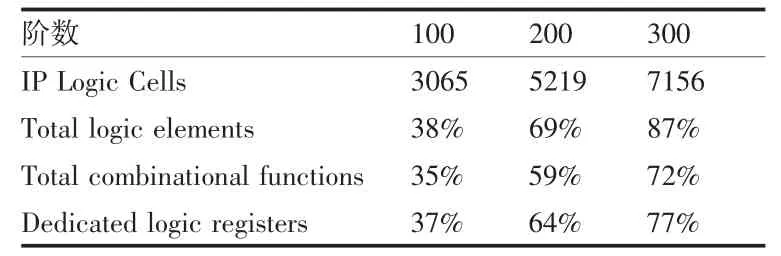
表2 資源利用率與階數的關系
3.3 2000階帶通濾波器的實現
2000階的FIR帶通濾波器實際輸出幅頻特性曲線如圖5所示。
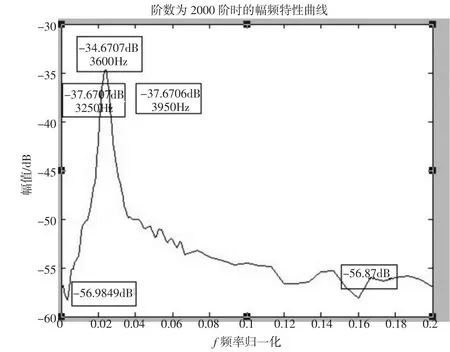
圖52000 階實際輸出幅頻特性曲線
由圖5可知,濾波器階數為2000階時的衰減特性可以滿足幅頻均衡的要求。
4 總結
本設計基于FPGA的IP Core實現了FIR數字帶通濾波器,并對如何保證濾波器性能的前提下有效地利用FPGA資源做出了分析。測試結果表明,濾波器階數設置合理,系統資源分配合理,保證了系統的正確性和有效性。
參考文獻:
[1]潘 松,黃繼業.EDA技術與VHDL[M].2版.北京:清華大學出版社,2007:14-16.
[2]求是科技.MATLAB7.0從入門到精通[M].北京:人民郵電出版社,2006:62-68.
[3]程佩青.數字信號處理教程[M].3版.北京:清華大學出版社,2009:40-45.
[4]Uwe Meyer-Baese.數字信號處理的FPGA實現[M].劉 凌,胡永生,譯,北京:清華大學出版社,2003:73-78.
[5]郝小江,繆志農,張小平.基于FPGA的FIR濾波器設計與實現[J].儀表技術,2010(1):25-26.

