衛星姿態控制用動量球模糊滑模控制*

李桂丹 鄒志強 李 斌

天津大學電氣自動化與信息工程學院，天津 300072

傳統微小衛星慣性執行機構主要為慣性動量輪[1](Reaction Wheel，RW)，若要完成衛星三軸姿態控制，RW及配套部件至少需要安裝3套。這種控制策略一方面限制了衛星的體積和重量，另一方面由于各軸輸出轉矩間存在耦合，增加了姿態控制算法的難度[2]。動量球(Reaction Sphere，RS)轉子不受機械約束，通過設定轉子旋轉軸的朝向及旋轉角速度，可以提供任意方向的轉矩。因此利用一個動量球替代原有多個動量輪的組合，可以消除耦合效應、提高控制精度[3]。

近些年對動量球的研究取得了很大進展。文獻[4]通過對定子正交繞組施加三相交流電，分別實現了轉子懸浮和旋轉運動。文獻[5]設計的動量球由8極轉子、20極定子組成，通過構建轉速和位置雙閉環控制系統，實現轉子連續運動控制。文獻[6]設計的RS通過增加垂直方向的定子繞組，實現了磁懸浮RS的旋轉控制。文獻[7]采用層狀定、轉子結構，通過采用轉矩分配的控制方法，實現了在給定區間內的任意角度姿態控制。

現有動量輪控制算法大部分采用歐拉角作為姿態描述量，導致動量球大角度運動時不可避免地會出現奇異現象。四元數作為另一種空間姿態描述量，無奇異現象且計算更為簡便[8]。文獻[9]運用四元數計算坐標變換矩陣，并結合機器視覺和神經網絡提出一種多自由度執行器轉子位置檢測方法；文獻[10]運用四元數描述轉子旋轉運動，并通過細化轉子期望軌跡實現球形步進電機的運動控制。另外，動量輪控制難點還在于轉子運動模型非線性、高耦合，以及實際控制中存在的數學模型不準確、參數漂移和外部擾動等不確定因素。

本文利用四元數的旋轉變換，構建了包含力矩、反電動勢、運動學及動力學模型在內的動量球數學模型。在此基礎上，采用滑模控制算法構建閉環控制系統[11]，根據軌跡跟蹤這一目標設計滑模切換函數，通過選擇趨近律設計滑模控制律，并驗證該滑模控制下系統的穩定性。引入模糊控制算法，根據系統狀態實時調整滑模控制律不連續項的系數，用于平滑控制信號，優化動量球滑模控制效果[12]，減小系統抖振現象。仿真結果表明，該算法跟蹤性能較好，且能克服模型誤差及外部擾動帶來的影響。

1 動量球建模

1.1 基本結構

常見的RS有多種不同結構，基于轉子旋轉軸全方位轉動考慮，本文選擇的控制對象為6-8多面體型[13]。如圖1所示，RS由定、轉子2部分組成，其中，8個永磁體磁極位于轉子內接正六面體的頂點、18個空心線圈位于定子內接正八面體的頂點和棱中點。

動量球在衛星中的安裝示意圖如圖2所示，定子通過支撐裝置固連于衛星內部。按照特定的控制策略給RS定子通電，可以驅動轉子旋轉或者偏轉，從而實現與衛星的動量交換。因此使用RS作為慣性執行機構控制衛星姿態，可以轉化為RS轉子目標軌跡跟蹤問題。

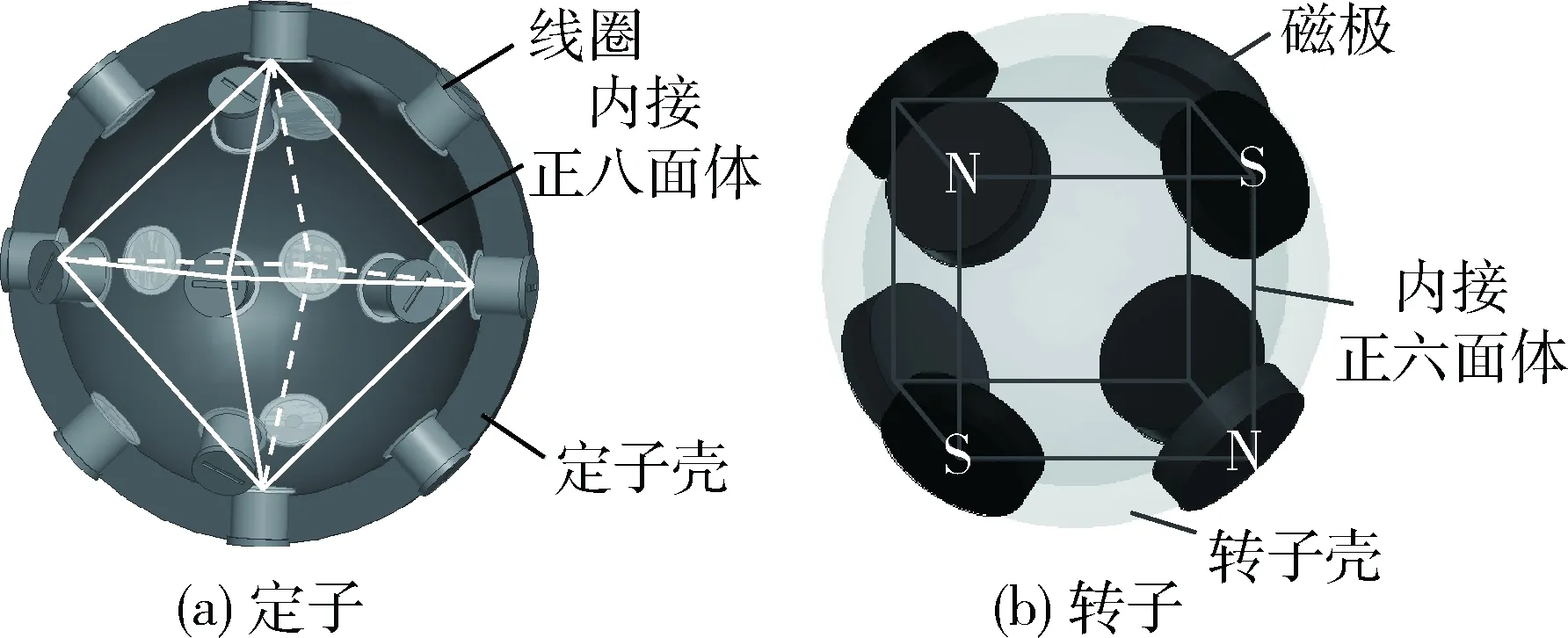
圖1 動量球結構示意圖

圖2 動量球安裝示意圖

1.2 力矩及反電動勢建模

由于動量球定子固定于衛星上，為便于后續公式推導，設定RS定子坐標系為慣性坐標系，轉子球心為坐標系原點。磁極i和線圈j的單位方向向量分別定義為ri和sj，若線圈j中的電流為ij，則轉子受到的控制力矩為

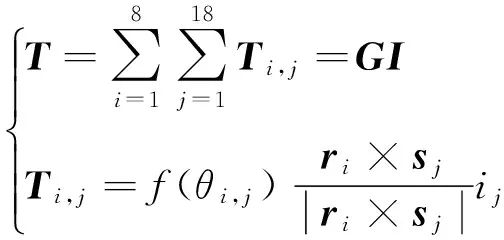
(1)

假定磁極i和線圈j間相對角速度為ωi,j，則線圈反電動勢為Ei,j=g(θi,j)ωi,j，其中g(θi,j)為反電動勢函數。根據疊加定理，RS定子反電動勢可表示為：

(2)

式(1)和(2)中，力矩函數f(θi,j)和反電動勢函數g(θi,j)均可通過有限元仿真及非線性擬合得到[14]。

若定子電壓為U，電阻及電感矩陣分別為R和L，參考異步電機電氣方程，可以求得RS電氣模型為

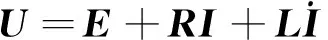
(3)

1.3 運動建模

根據牛頓-歐拉剛體旋轉定理以及四元數特性，可以推導出RS轉子的運動學模型及動力學模型[15]分別為

(4)

(5)

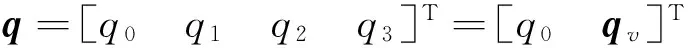
綜合上述模型，得到模擬動量輪運行原理的數學模型如圖3所示。動量球運行時，施加在動量輪定子的電壓U，其一部分抵消由于轉子旋轉產生的反電動勢E，另一部分在定子線圈中生成電流I，并與轉子磁極相互作用產生電磁力矩T，最終推動RS轉子，使其運動狀態發生變化。

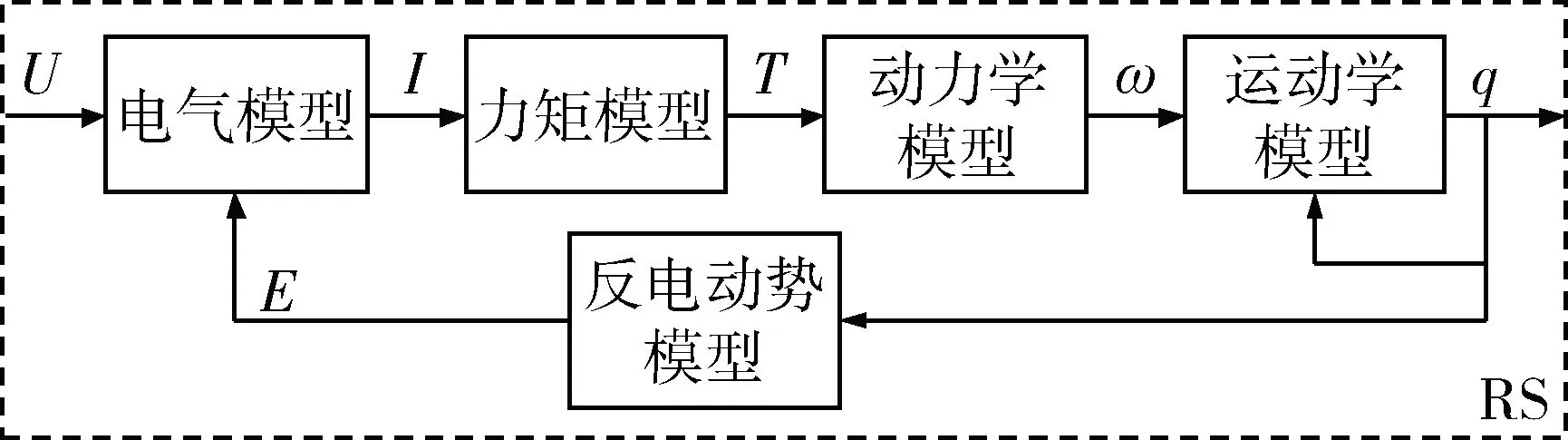
圖3 動量球數學模型框圖

2 模糊滑模控制器設計

假設RS轉子當前及目標姿態四元數分別為qc和qd，則誤差四元數可通過下式求得：

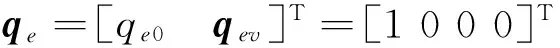
2.1 滑模控制器設計

滑模變結構控制研究的主要問題是設計適當的切換函數和滑模控制律，使得系統能在有限時間內到達滑模流形，實現滑動模態運動。

設計滑模控制切換函數為：

S=ωe+Cqev

(6)

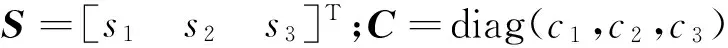
由下述分析可知，在滑模流形S=0上，RS的系統是穩定的。在滑模流形上ωei=-ciqei，i=1,2,3恒成立，結合RS轉子運動學模型式(4)，可以得到誤差四元數滿足：

為簡化推導過程，設置滑模切換函數中參數滿足條件c1=c2=c3。則誤差四元數滿足以下4個獨立的微分方程：

其中，λ0>0，λi<0，i=1,2,3，因此可以判斷誤差四元數矢量部分qev漸近收斂于0。由于ωe與qev成比例關系，所以誤差角速度ωe也漸近收斂于0，也即RS轉子始終跟蹤目標軌跡。

合理的滑模控制律應保證系統在偏離滑模流形時，趨近速度大；到達滑模流形時，趨近速度小。針對這一特性，本文采用趨近函數法設計滑模控制器，選取指數趨近律：

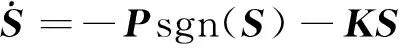
(7)

其中，sgn為符號函數；K=diag(k1,k2,k3)和P=diag(p1,p2,p3)均為正定矩陣。結合滑模流形式(6)可以求出滑模等效控制律為：

(8)

設計滑模控制律：

T=Te-KS-Psgn(S)

(9)

其中，

為轉子姿態四元數矢量部分的運動學模型。

前述已知在滑模流形上系統趨于穩定，下面對偏離滑模流形的系統在滑模控制律式(9)作用下的穩定性進行分析。

構造Lyapunov函數為：

(10)

Vs為半正定函數，當且僅當S=0有Vs=0。對式(10)求導可以得到：

將滑模控制律式(9)帶入上式，可以得到

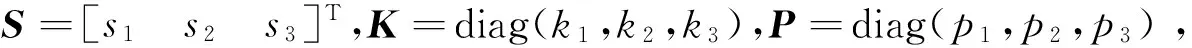
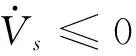
2.2 模糊控制器設計

滑模控制律式(9)中的Psgn(S)部分為不連續項，參數P設置過大會引起系統出現較大的抖振。根據趨近律式(7)，可以解出系統由初始狀態S0到達滑模流形S=0的時間為：

可以看出，當控制項參數K為定值時，增大切換項參數P可以加快趨近速度。因此引入模糊控制動態調整系數P，使得系統同時滿足到達段趨近速度較大、滑模段抖振較小。

模糊控制器設計如下：

{NB,NM,NS,ZE,PS,PM,PB}，分別代表負大、負中、負小、零、正小、正中和正大；

{ZE,VS,S,SB,MB,B,VB}，分別代表0、很小、小、小大、中大、大和很大。

2)為改善滑模控制系統性能，當系統狀態遠離滑模流形時，pi應取較大值；當系統狀態接近滑模流形時，pi應取較小值。根據這一依據，設定模糊控制規則表如表1所示。

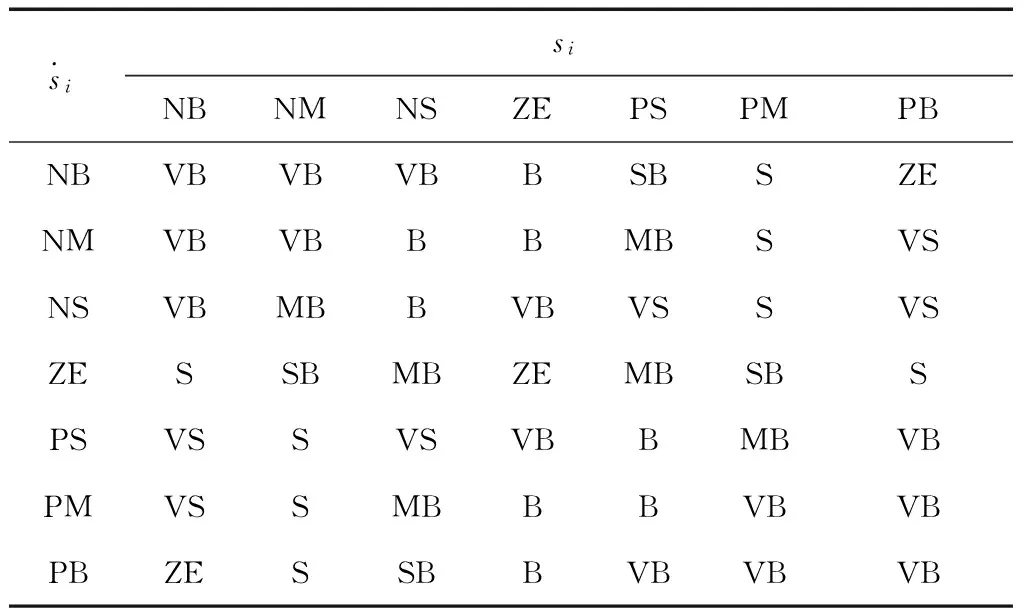
表1 模糊控制規則表

3)設定輸入輸出隸屬度函數均為三角型，輸出解模糊化選用重心法。

綜上所述，可得到動量球整體控制框圖如圖4所示：qd為調整衛星姿態所需的RS轉子運動軌跡，根據轉子當前位置qc，計算得到轉子轉動所需控制力矩T，并最終得到動量球定子電壓U。虛線框中模型與RS數學模型相對應，用于實現力矩到定子電壓的轉換。

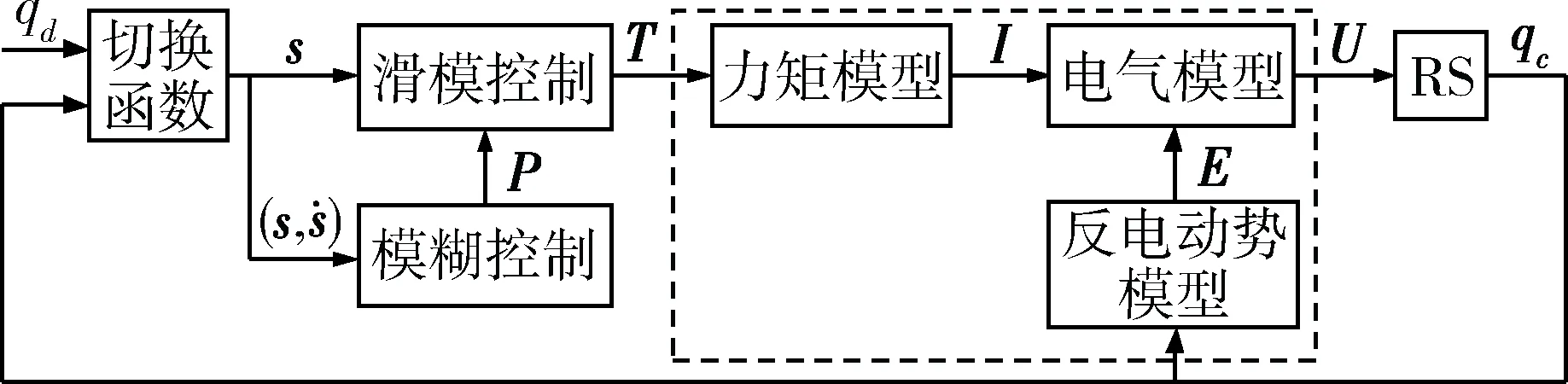
圖4 RS整體控制框圖

3 仿真分析

為驗證所提出的RS控制算法的有效性，利用MATLAB/SIMULINK搭建仿真平臺，對計算轉矩法、滑模控制和模糊滑模控制3種算法進行仿真對比。仿真中動量球的參數設置為：定子電阻R=1.46Ω；定子電感L=0.48mH；轉子轉動慣量Jx=Jy=Jz=6.48kg·m2。為驗證算法的魯棒性，增加模型誤差ΔJi=1.2kg·m2，i=x,y,z；外界干擾TE=[10 10 10]TN·m(5s≤t≤6s)。

控制系數設置如下：計算轉矩法Kp=diag(30,30,30)，Kd=diag(20,20,20)；滑模控制及模糊滑模控制K=diag(10,10,10)，C=diag(10,10,10)，P=diag(8,8,8)。假定RS轉子初始位置為[0 0 0 1]T，目標軌跡為[0 costsint0]T。當仿真時長設為10s時，3種控制方法仿真結果分別如圖5～7所示。

對比圖5(a)及6(a)可以看出，相比于傳統的計算轉矩法，在滑模控制下，RS有更快的響應速度和更高的跟蹤精度；外界擾動對跟蹤效果幾乎無影響，體現出很強的魯棒性。但如圖6(b)所示，滑模控制的穩態力矩仍有較大值且高頻顫振，不僅增加了能量消耗，增大了電流跟蹤控制的難度，也容易導致控制器部件的損壞[11]。

對比圖6(a)及7(a)可以看出，引入模糊控制后的滑模控制保留了原有的快速、高精度跟蹤性能，盡管抗擾動能力略有下降，但仍體現出對于不確定因素的強魯棒性。此外，對比圖6(b)及7(b)可以發現，引入模糊控制后，穩態時力矩顫振幅度僅為原有的1/8左右，滑模控制固有的抖振現象得到大幅度改善。

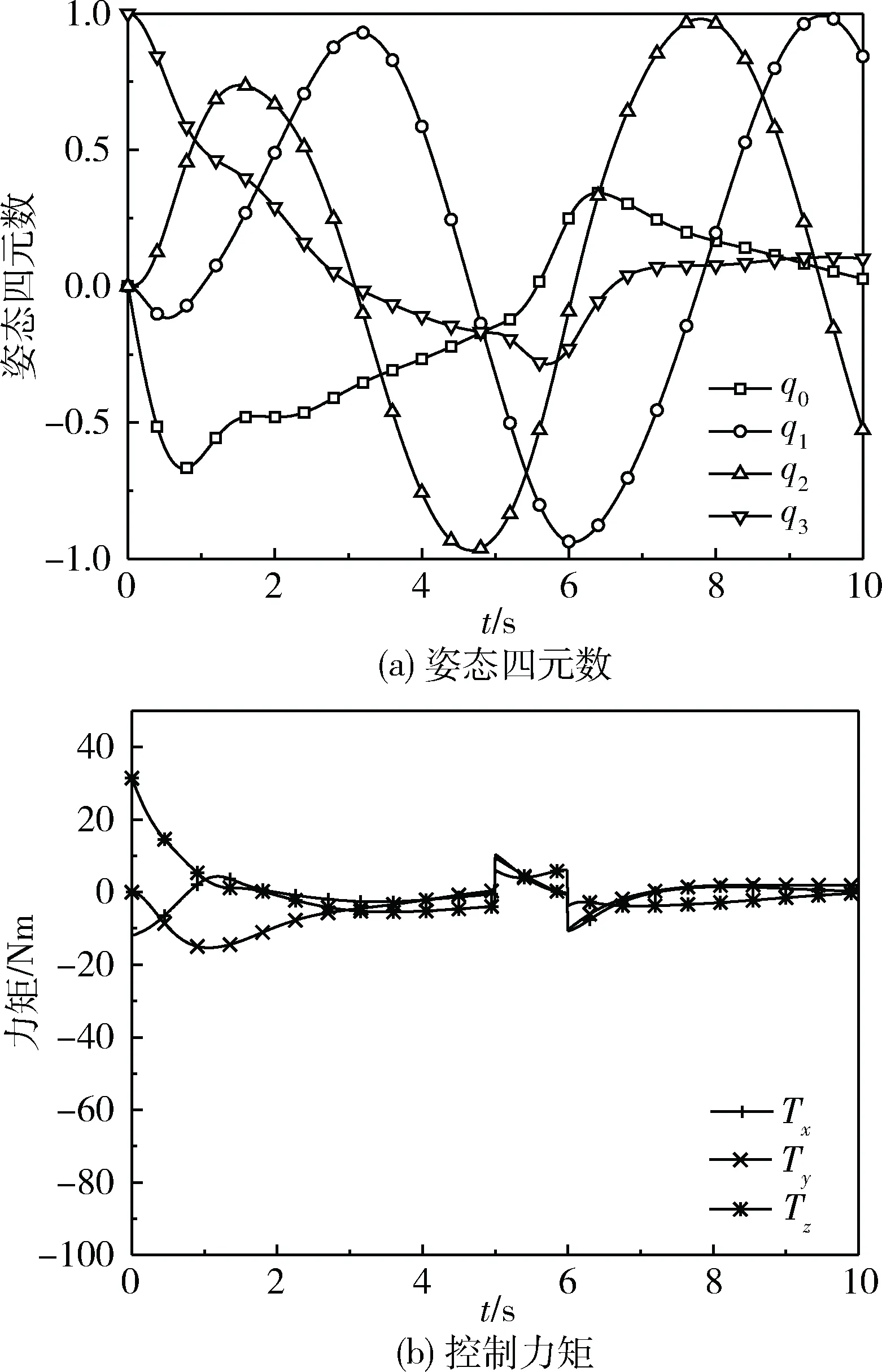
圖5 計算轉矩法仿真結果

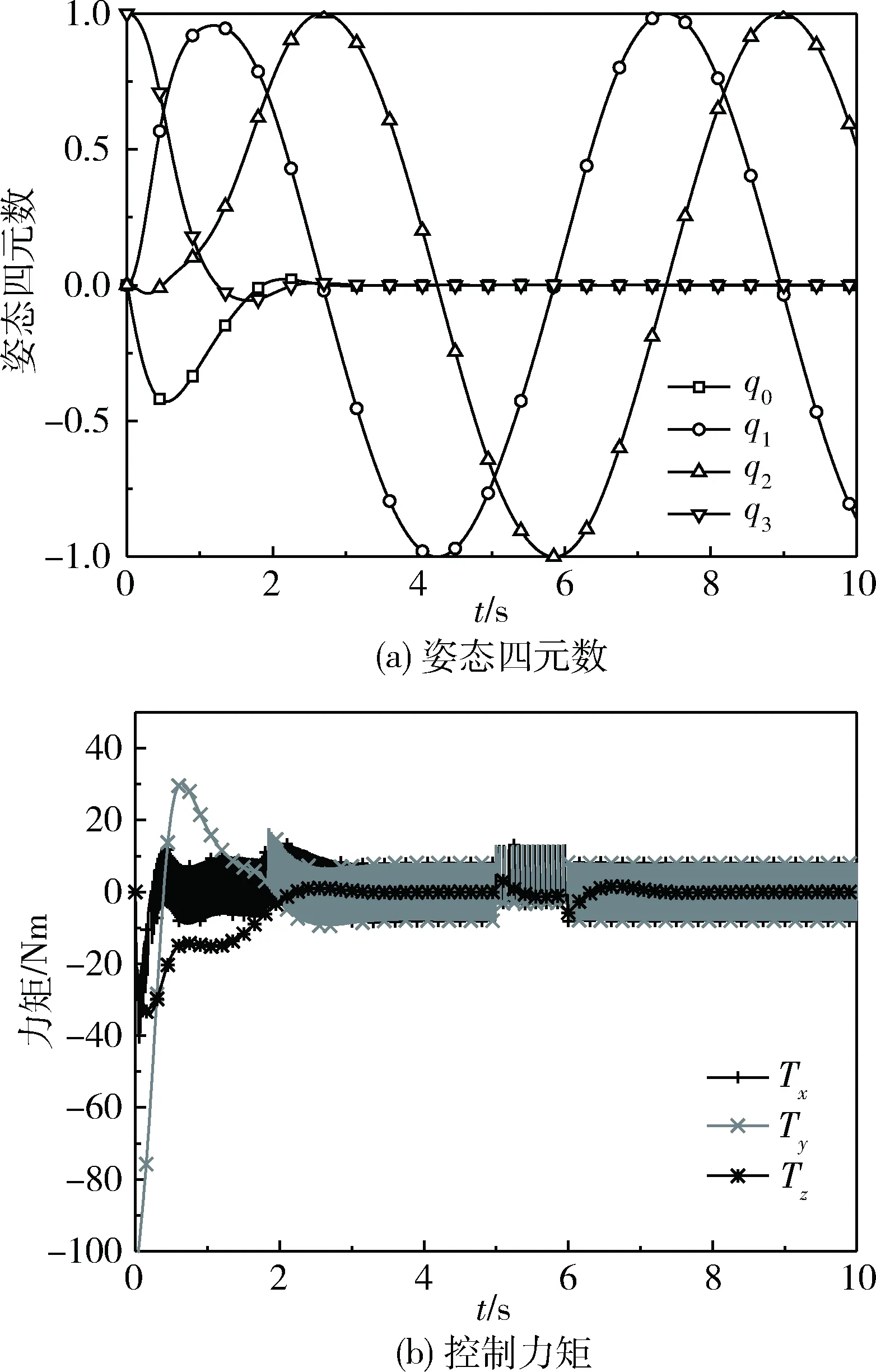
圖6 滑模控制仿真結果

圖7 模糊滑模控制仿真結果

4 結論

提出一種動量球的模糊滑模控制算法，該方法以四元數作為姿態描述量，建立了動量輪整體模型，采用滑模控制，克服了動量球的模型誤差和外界擾動等不確定因素，引入模糊控制，進一步改善了滑模控制帶來的抖振現象，優化了控制效果。仿真結果表明，該算法能使動量球較好地跟蹤目標軌跡。

[1] 王獻忠,張肖,張麗敏. 近地零動量衛星干擾力矩飛輪補償控制[J]. 航天控制,2016,34(2):60-65. (Wang X Z，Zhang X，Zhang L M. Disturbance Moment Control Based on Wheel for Zero-Momentum Near Earth Satellites [J]. Aerospace Control, 2016, 34(2):60-65.

[2] Zhu L Y, Guo J, Gill E. Reaction Sphere for Microsatellite Attitude Control[C]. Proceedings of the International Astronautical Congress, IAC, 2016:26-30.

[3] 房建成,孫津濟,樊亞洪. 磁懸浮慣性動量輪技術[M]. 國防工業出版社, 2012:20-22.(Fang J C, Sun J J, Fan Y H Magnetically Suspended Inertial Momentum Wheel Technology[M]. Nation Defense Industry Press, 2012:20-22.)

[4] Zhu Y, Chen A, Zhang M, et al. A Novel Electrodynamic Suspension Reaction Sphere (EDSRS) for Satellite Attitude Control[C]. Proceedings of the 16th International Conference of the European Society for Precision Engineering and Nanotechnology, 2016.

[5] Rossini L, Onillon E, Boletis A, et al. Development and Closed-loop Experimental Results of a Reaction Sphere Elegant Breadboard[C]. 16th European Space Mechanisms and Tribology Symposium, 2015:52-57.

[6] D K Kim, H J Yoon, W Y Kang. Development of a Spherical Reaction Wheel Actuator Using Electromagnetic Induction[J]. Aerospace Science and Technology, 2014, (39):86-94.

[7] Li B, Yu R J, Li H K, et al. Modeling and Analysis of a 3-DOF Spherical Momentum Exchange Actuator for Spacecraft Attitude Maneuver[J]. Journal of Aerospace Engineering, 2015, 28(6).

[8] Diebel, James. Representing Attitude: Euler Angles, Unit Quaternions, and Rotation Vectors[J]. Matrix, 2006, 58(15):1-35.

[9] Li Z. Neural Network Based Multisensor Fusion in a Novel Permanent Magnet Multi-dof Actuator Orientation Detection System[J]. International Journal on Smart Sensing and Intelligent Systems, 2012, 5(4):911-927.

[10] Wang Q J, Xia K. The Motion Control Algorithm Based on Quaternion Rotation for a Permanent Magnet Spherical Stepper Motor[C]. 2006 CES/IEEE 5th International Power Electronics and Motion Control Conference, 2006, (2):1-5.

[11] 劉金琨,孫富春. 滑模變結構控制理論及其算法研究與進展[J]. 控制理論與應用,2007,(3):407-418. (Liu J K, Sun F C. Research and Development on Theory and Algorithms of Sliding Mode Control[J]. Control Theory & Applications, 2007, (3):407-418.)

[12] 劉紅俐,張鵬,朱其新,胡壽松. 基于新型趨近律的積分模糊滑模控制及其在PMSM控制中的應用[J]. 航天控制,2014,32(6):81-87.(Liu H L, Zhang P, Zhu Q X, et al. The Integral Fuzzy Sliding Mode Control Based on a Novel Reaching Law and Its Applications on the Control of PMSM[J]. Aerospace Control, 2014, 32(6):81-87.)

[13] Tomoaki Y. Simulation Results of a Hexahedron-octahedron Based Spherical Stepping Motor[J]. Journal of Mechanical Science & Technology, 2010, 24(1):33-36.

[14] 劉敬猛,孟艷艷,陳偉海,吳星明. 三自由度永磁球形電機的建模和電壓控制[J]. 吉林大學學報(工學版),2014,44(2):560-566.(Liu J M, Meng Y Y, Chen W H, et al. Model and Control of a PM Spherical Actuator Based on Voltage Model[J]. Journal of Jilin University(Engineering and Technology Edition), 2014,44(2):560-566.)

[15] L L Show, J C Juang, Y W Jan, et al. Quaternion Feedback Attitude Control Design: a Nonlinear H∞Approach[J]. Asian Journal of Control,2003, 5(3):406-411.