基于渦環尾跡模型的共軸剛性旋翼直升機飛行動力學建模

袁野,陳仁良,李攀

南京航空航天大學 直升機旋翼動力學國家級重點實驗室，南京 210016

共軸剛性旋翼直升機是目前高速直升機研究的主要方向之一。其主要特點是采用了前行槳葉概念旋翼，降低了后行槳葉揮舞，從而減小了上下旋翼間距，降低高速前飛時的廢阻功率，提高直升機性能。但是，減小旋翼間距會增加共軸剛性旋翼間氣動干擾的復雜性。由于旋翼間距較小，在相同前進比下，上旋翼的尾跡對下旋翼的干擾影響明顯增強，顯著改變下旋翼的氣動力特性和尾跡。下旋翼氣動力特性和尾跡對上旋翼的軸向來流與尾跡的影響也由于旋翼間距的減小而更為明顯，進而引起上旋翼的氣動力變化[1]。這些特性都會改變共軸剛性旋翼直升機的飛行動力學特性。常規的動態入流等入流模型難以準確計算旋翼間氣動干擾情況[2-5]。計算流體力學[6]以及旋翼黏性渦粒子方法[7-8]等雖然能夠得到旋翼間氣動干擾結果，但計算耗時普遍較長，難以適用于飛行動力學計算。因此，如何在飛行動力學模型中較為準確而快速地計算旋翼間氣動干擾是共軸剛性旋翼直升機發展中亟需解決的重要問題。

國內外針對共軸剛性旋翼直升機飛行動力學中的旋翼氣動干擾問題已有一定研究。Ruddell等[9-11]根據風洞和飛行試驗的結果發現旋翼間氣動干擾會影響共軸剛性旋翼直升機的飛行動力學特性，并利用一系列經驗系數來模擬旋翼間氣動干擾。這一經驗系數是通過某一機型的風洞與飛行試驗確定的，因此不能廣泛運用到其他共軸剛性旋翼直升機中；Leishman等[12-14]根據共軸旋翼的尾跡畸變特性, 發展了基于動量葉素理論的軸流狀態下共軸旋翼入流模型，但不適用于前飛時的飛行動力學特性計算。近年來，很多研究者[15-20]通過自由尾跡方法對共軸旋翼在懸停和前飛時的氣動特性進行研究，但這一方法計算耗時仍相對較長。趙珅寧等[21-22]基于旋翼渦流理論基礎，提出了一種新的旋翼動態尾跡模型，該模型采用6自由度渦環單元來表示旋翼尾跡渦系，可描述機動飛行中旋翼尾跡動態畸變行為，具有應用于實時飛行仿真的潛力。這一方法為解決共軸剛性旋翼直升機飛行動力學中的旋翼間氣動干擾問題提供了新的思路。

鑒于此，本文以渦環單元動態尾跡模型為基礎，建立適用于旋翼間氣動干擾計算的共軸旋翼氣動力模型，并以相關文獻中的風洞試驗數據為對照，在懸停和前飛狀態下驗證該模型。然后，將這一氣動力模型代入到共軸剛性旋翼直升機飛行動力學模型中，以XH-59A直升機為研究對象，計算在前進比為0～0.4時的配平特性，并與飛行試驗結果進行比對。依據配平特性和不同前飛速度時配平狀態下的旋翼尾跡，分析共軸剛性旋翼直升機中旋翼間氣動干擾對配平特性的影響及其原因。

1 共軸剛性旋翼渦環單元動態尾跡模型

1.1 模型概述

本文中共軸旋翼所使用的渦環單元動態尾跡模型以文獻[21-22]為基礎，依據無限片槳葉假設的作用盤理論以及經典固定尾跡模型構建。在該模型中，考慮了尾跡的各種畸變效應。因此可以用于計算徑向、軸向和周向誘導速度對自由渦延伸方向的影響。這一動態尾跡模型的簡化過程如圖1所示。

根據圖1，在尾跡模型中，圓柱渦系環量中的垂向分量對槳盤上的誘導速度影響較小，因此只考慮其水平分量。將尾跡離散成若干個帶狀渦環，其長度分別為l1,l2,…,ln。若渦管上渦強的線密度為γ，則第n個渦帶上的渦量則為Γn=γln，然后將帶狀渦環簡化成一個集中渦環,γ可以通過葉素理論得到的旋翼升力系數CL、氣動俯仰力矩系數Cm和氣動滾轉力矩系數Cl給出，具體方法可參考文獻[23]。ln通過式(1)計算，即

ln=Δt(v0+wh)

(1)

式中：Δt為時間步長；v0為當前槳盤的平均誘導速度；wh為槳盤的垂向速度。

離散后的每個集中渦環單元具有6個剛體運動自由度和1個半徑伸縮收展自由度。因此，第i個渦環運動狀態向量可以用Ri= [xiyiziθxiθyiθziri]表示，xi、yi、zi為第i個渦環的位置坐標，θxi、θyi、θzi為渦環的俯仰角、滾轉角和偏航角，ri為第i個渦環的渦環半徑。

1.2 共軸旋翼尾跡模型

共軸旋翼氣動干擾現象相比于常規單旋翼更為復雜，主要可分為兩種特征[24]：

1)上下旋翼的尾跡會分別對另外一副旋翼的誘導速度產生影響。

2)上下旋翼的尾跡會分別對另外一副旋翼拖出的尾跡延伸運動產生影響。

值得注意的是，以上兩種氣動干擾特征在共軸旋翼中是相互耦合的。即上下旋翼的尾跡在直接影響另外一副旋翼誘導速度的同時，也會通過改變其尾跡延伸運動而間接影響另外一副旋翼的誘導速度，反之亦然。這一耦合特性使共軸旋翼的氣動干擾問題更為復雜。為了解決這一問題，本文采用共軸旋翼渦環單元動態尾跡模型。上下旋翼拖出尾跡中第i個渦環的狀態微分方程可以表示為

(2)

(3)

式中：下標u、l分別表示上旋翼和下旋翼；vi(uh,Ri)為旋翼線運動和角運動誘導速度的相對運動速度；uh為旋翼運動速度和角速度列向量；ui(R)為尾跡對渦環單元的誘導速度，這一速度是通過基于畢奧-薩瓦爾定律構建的微分方程組得到的，具體求解步驟可參考文獻[21]。

根據式(2)和式(3)，得到渦環運動的微分方程組，計算上下旋翼的渦環系運動隨時間的變化趨勢。根據上下旋翼的渦環系Ru和Rl的空間位置及渦環系中每個渦環單元的渦量Γ能夠得到空間內任意一點處上下旋翼尾跡疊加的誘導速度隨時間的變化趨勢，進而得到槳盤上不同時間下的誘導速度分布。通過旋翼氣動力計算模型以及旋翼揮舞運動模型可以得到該共軸旋翼氣動力模型的基本計算流程，如圖2所示。

根據圖2，在氣動力計算中，本文利用響應法求解旋翼氣動力，計算渦環系微分方程組隨時間推進的過程。其中虛線表示上下旋翼間氣動干擾的耦合項計算流程。

當上下旋翼的誘導速度隨時間的變化小于殘差條件時，可認定為旋翼氣動力穩定。通過揮舞運動模型和氣動力計算模型得到旋翼氣動力和渦強線密度γ。然后重復上述過程，當上下旋翼氣動力變化滿足殘差條件時結束計算，并得到最終旋翼誘導速度分布以及旋翼氣動力大小。

從圖2中可以看出，在計算過程中，上下旋翼尾跡渦環系都會受到另外一組渦環系的影響。上下旋翼槳盤誘導速度分布也是由上下旋翼渦環系所共同確定的。因此該共軸旋翼氣動力模型考慮到了共軸旋翼間氣動干擾的兩種主要特征。

2 共軸旋翼氣動力模型驗證

本文采用文獻[25-26]中的共軸旋翼風洞試驗數據，驗證本文的共軸旋翼渦環單元動態尾跡模型的準確性。風洞試驗旋翼系統基本參數見表1。

根據試驗狀態，選擇前進比μ=0(懸停狀態)和μ=0.15(小速度前飛狀態)情況。共軸旋翼在懸停狀態和小速度前飛狀態下旋翼間氣動干擾更為嚴重[27]。因此這兩個狀態可以用于驗證本模型對共軸旋翼間氣動干擾的計算精度。此外，根據風洞試驗要求，上下旋翼反扭矩系數mk都必須相等。上下旋翼所產生的升力系數CL隨mk的變化趨勢比對結果如圖3所示。

根據圖3的結果，在懸停和前飛時，基于渦環單元動態尾跡的共軸旋翼氣動力模型與風洞試驗結果比對良好。說明該共軸旋翼氣動力模型能夠計算懸停和前飛狀態時考慮氣動干擾的共軸旋翼氣動力特性。因此可以將其運用到共軸剛性旋翼直升機飛行動力學模型中。

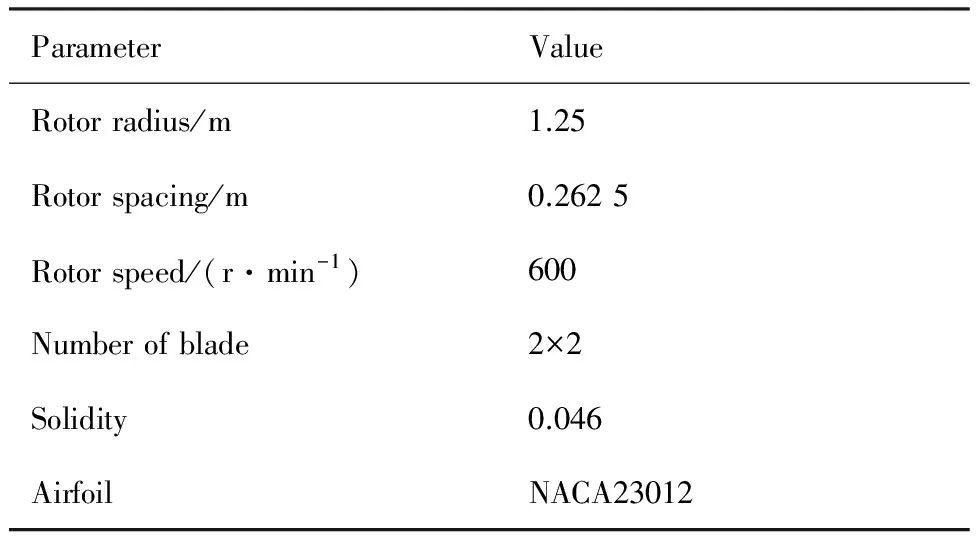
表1 氣動力試驗共軸旋翼參數Table 1 Parameters of coaxial rotor in aerodynamic test

3 飛行動力學模型驗證與分析

3.1 模型驗證

以上述共軸旋翼氣動力模型為基礎，建立共軸剛性旋翼直升機飛行動力學模型。該共軸剛性旋翼直升機包括旋翼模型、機身模型、平尾模型以及垂尾模型。其中旋翼模型除了基于渦環尾跡模型的入流模型外，還包括采用等效揮舞概念構建的適用于剛性旋翼的揮舞運動方程，以及基于二維翼型氣動力數據表的氣動力計算模型。機身、平尾和垂尾模型是基于相關風洞試驗數據構建的。該飛行動力學模型中其他部分的建模方法來自文獻[28]。

在配平計算中，共軸剛性旋翼直升機機體的線加速度、角加速度和角速度均為零，并且剛性旋翼的揮舞角速度和揮舞角加速度也為零。因此可得共軸剛性旋翼直升機的平衡方程為

(4)

(5)

(6)

(7)

式中：X、Y、Z以及L、M、N分別為共軸剛性旋翼飛行器所受到的氣動力和力矩；mSUM為全機質量；θ為機體俯仰角；φ為機體滾轉角；g為重力加速度；K和F分別為旋翼揮舞剛度矩陣和揮舞運動外激勵項，可通過揮舞方程進行計算；a0、a1、b1分別為旋翼錐度角、旋翼揮舞后倒角和旋翼揮舞側倒角。在配平計算中，配平量包括旋翼總距、縱向和橫向周期變距、總距差動，機身俯仰角和滾轉角以及上下旋翼的旋翼錐度角、后倒角和側倒角，共12個配平量，與平衡方程個數相同，因此可以利用非線性方程求解方法進行配平。

本文以XH-59A共軸剛性旋翼直升機為研究對象，該直升機的基本數據如表2所示。

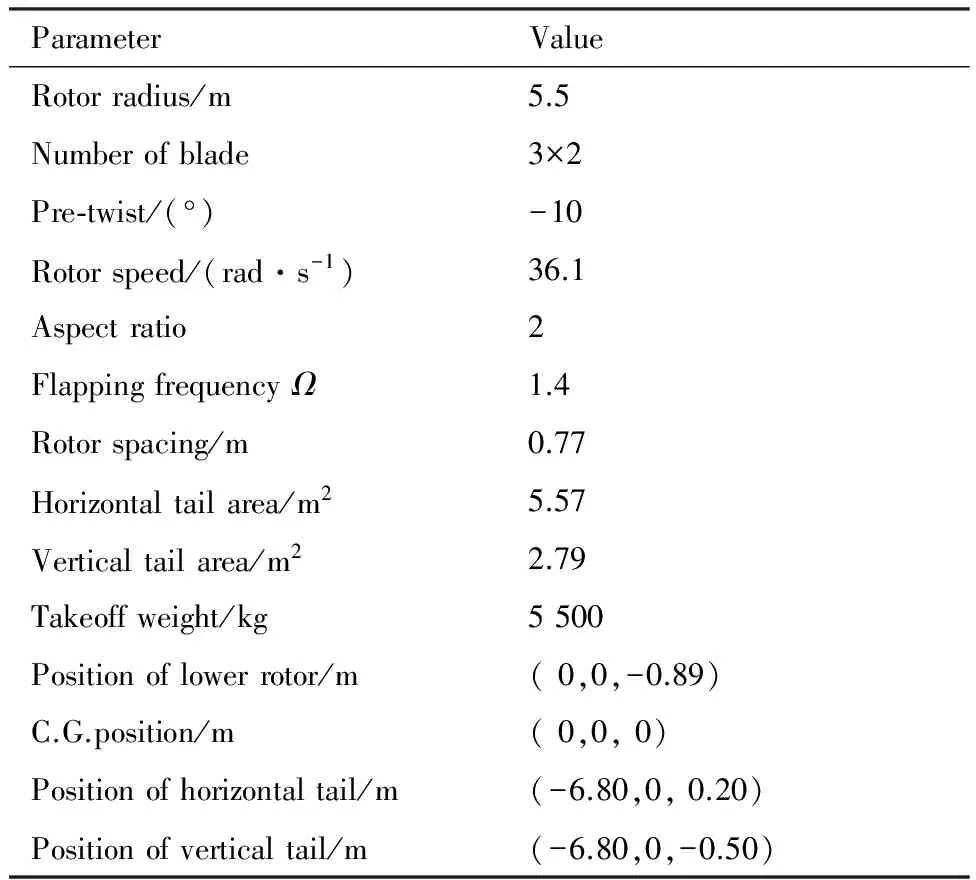
表2 XH-59A共軸剛性旋翼直升機參數

通過本文提出的飛行動力學模型計算得到配平結果，在μ=0～0.4 (0～80 m/s)速度范圍內與相關飛行試驗數據配平結果機型對比，如圖4所示。

另外，對比結果中還加入了基于不考慮旋翼氣動干擾的渦環單元動態尾跡模型的共軸剛性旋翼直升機配平結果(即不考慮圖2計算過程中虛線部分的上下旋翼間耦合項)。通過與考慮旋翼間氣動干擾的配平計算結果對比說明氣動干擾對共軸剛性旋翼直升機配平特性的影響。

根據配平對比結果，可以得出以下結論：

1) 在μ=0～0.4(0～80 m/s)速度范圍內，本文采用的飛行動力學模型與飛行試驗數據對比良好，說明該模型能夠反映在旋翼間存在氣動干擾下的共軸剛性旋翼直升機的配平特性。

2) 通過與不考慮旋翼間氣動干擾的模型配平結果對比發現，旋翼間干擾對懸停和低速前飛時的共軸剛性旋翼直升機的配平總距、配平總距差動以及配平縱向周期變距影響較大。另外，配平結果顯示，在低速前飛時，配平縱向周期變距隨前飛速度呈負梯度變化。關于這些問題的討論，將在3.2節中展開。

3) 在不同的前飛速度下，該模型配平計算時間與本課題組已有的自由尾跡方法[29-30]計算共軸直升機配平所需時間的對比如圖5所示(計算設備為英特爾Core i5-4590 臺式機電腦)。利用基于渦環尾跡模型的共軸剛性旋翼直升機飛行動力學模型的配平計算時間一般在100～200 s。課題組基于自由尾跡的常規單旋翼直升機飛行動力學模型的配平計算時間均在1 400 s以上。可見，渦環尾跡模型的計算效率明顯高于自由尾跡方法。

3.2 配平特性分析

為了分析氣動干擾對共軸剛性旋翼直升機飛行動力學特性的影響，本文通過考慮氣動干擾的渦環單元動態尾跡模型得到了不同前進比下配平時的尾跡形狀，如圖6所示。同時，根據渦環模型得到上下旋翼槳盤前緣到后緣的誘導速度分布，如圖7所示,R為槳葉半徑，-1.0表示槳盤前緣 (180°方位角)槳尖位置，1.0表示槳盤后緣 (0°方位角)槳尖位置。

1) 當μ=0(懸停狀態)時，旋翼間氣動干擾相對嚴重，下旋翼大部分面積位于上旋翼尾跡區域內，增加了共軸旋翼尤其是下旋翼的垂向來流速度，降低了旋翼總距給定時旋翼所產生的氣動升力，如圖6(a)所示。因此，在氣動干擾的影響下，直升機需要提高配平總距保證升力平衡，這與圖4(a)的結果一致。從圖7(a)還可以看出，由于下旋翼受到氣動干擾的影響更嚴重，下旋翼槳盤上的誘導速度明顯大于上旋翼，上下旋翼所產生的反扭矩不同，直升機需要施加額外的總距差動來保證反扭矩平衡，如圖4(c)總距差動配平結果所示。另外，由于各周向方位處旋翼間干擾引起的來流速度均相等，上旋翼對下旋翼的干擾不會產生額外的抬頭或者低頭力矩，此時配平縱向周期變距為0。

2) 當速度V=20 m/s,μ=0.1時，旋翼間氣動干擾仍會增加配平總距和總距差動，如圖6(b)所示。在這一速度階段內，上旋翼的尾渦會明顯增大下旋翼槳盤上后緣處(0°方位角附近)的誘導速度，如圖7(b)所示。其結果是減小這一區域產生的氣動升力，進而產生俯仰方向的揮舞氣動力矩。由于共軸剛性旋翼的揮舞頻率約為1.4Ω，揮舞響應滯后角為30°左右[31]，因此揮舞方程中的俯仰氣動力矩會對機體產生俯仰方向的力矩，進而增加配平所需的縱向周期變距。

3) 當V=40 m/s,μ=0.2時，隨著前飛速度的進一步提高，旋翼間氣動干擾會隨著尾跡傾斜角的增加而逐漸變弱，因此對配平總距和總距差動的影響也逐漸減小，如圖4(a)和圖4(c)所示。通過對比圖7(b)和圖7(c)，還可以看出上旋翼的尾跡對下旋翼槳盤后緣處的影響隨著前飛速度的提高而降低，減小了抬頭力矩。這使得配平所需的縱向周期變距減小，進而導致縱向周期變距出現了隨前飛速度增加而呈負梯度變化的情況。

4 結 論

本文基于渦環單元動態尾跡模型，發展了適用于旋翼間氣動干擾計算的共軸旋翼氣動力模型，并以此為基礎建立了共軸剛性旋翼直升機飛行動力學模型。開展了在考慮氣動干擾影響下的共軸剛性旋翼直升機配平特性計算、驗證與分析工作。

1) 根據相關比對結果，說明本文提出的基于渦環尾跡的共軸剛性旋翼直升機飛行動力學模型可以準確地計算共軸剛性旋翼直升機的配平特性，進而為相關飛行動力學特性的計算和研究奠定基礎。

2) 共軸剛性旋翼直升機的旋翼間氣動干擾會增加懸停與低速前飛時的配平總距和總距差動。隨著前飛速度的提高，氣動干擾對總距和總距差動配平結果的影響逐漸降低。

3) 共軸剛性旋翼直升機在低速前飛時會產生縱向周期變距負梯度現象。這一現象是上下旋翼間氣動干擾和共軸剛性旋翼較低的揮舞響應滯后角兩者共同作用造成的。

參 考 文 獻

[1] 陳仁良， 李攀， 吳偉， 等. 直升機飛行動力學數學建模問題[J]. 航空學報, 2017, 38(7): 720915.

CHEN R L, LI P, WU W, et al. Mathematical modeling of helicopter flight dynamics[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 720915 (in Chinese).

[2] 徐冠峰, 陳銘. 小型共軸式直升機旋翼槳葉鉸鏈力矩研究[J]. 航空動力學報, 2010, 25(8): 1805-1810.

XU G F, CHEN M. Research on rotor blade hinge moment of a small-scale coaxial helicopter[J]. Journal of Aerospace Power, 2010, 25(8): 1805-1810 (in Chinese).

[3] FERGUSON K, THOMSON D. A performance analysis of compound helicopter configurations[C]∥The AHS 70th Annual Forum. Alexandria, VA: The AHS International, Inc., 2014.

[4] FERGUSON K, THOMSON D. Flight dynamics investigation of compound helicopter configurations[J]. Journal of Aircraft, 2013, 52(1):1-12.

[5] 袁夏明, 朱紀洪, 毛漫. 共軸式無人直升機建模與魯棒跟蹤控制[J]. 控制理論與應用, 2014, 31(10): 1285-1294.

YUAN X M, ZHU J H, MAO M. Modeling and robust tracking control for coaxial unmanned helicopter [J]. Control Theory & Applications, 2014, 31(10):1285-1294 (in Chinese).

[6] 朱正, 招啟軍, 李鵬. 懸停狀態共軸剛性雙旋翼非定常流動干擾機理[J]. 航空學報, 2016, 37(2): 568-578.

ZHU Z, ZHAO Q J, LI P. Unsteady flow interaction mechanism of coaxial rigid rotor in hover [J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 568-578 (in Chinese).

[7] SINGH P, FRIEDMANN P P. Application of vortex methods to coaxial rotor wake and load calculations[C]∥55th AIAA Aerospace Sciences Meeting. Reston, VA: AIAA, 2017.

[8] RAJMOHAN N, ZHAO J, HE C. A coupled vortex particle/CFD methodology for studying coaxial rotor configurations[C]∥Fifth Decennial AHS Aeromechanics Specialists’ Conference. Alexandria, VA: The AHS International, Inc., 2014.

[9] RUDDELL A J. Advancing blade concept (ABCTM) development[J]. Journal of the American Helicopter Society, 1977, 22(1): 13-23.

[10] RUDDELL A J, MACRINO J A. Advancing blade concept (ABC) high speed development[C]∥American Helicopter Society 36th Annual Forum. Alexandria, VA: The AHS International, Inc., 1980.

[11] RUDDELL A J, GROTH W, MCCUTCHEON R. Advancing blade concept (ABC) technology demonstrator: USAAVRADCOM-TR-81-D-5 [R]. 1981.

[12] LEISHMAN J G, ANANTHAN S. Aerodynamic optimization of a coaxial proprotor[C]∥Proceedings of the 62th Annual Forum American Helicopter Society International. Alexandria, VA: The AHS International, Inc., 2006.

[13] LEISHMAN J G, SYAL M. Figure of merit definition for coaxial rotors[J]. Journal of the American Helicopter Society, 2008, 53(3): 290-300.

[14] SYAL M, LEISHMAN J G. Aerodynamic optimization study of a coaxial rotor in hovering flight[J]. Journal of the American Helicopter Society, 2012, 57(4): 1-15.

[15] BAGAI A, LEISHMAN J G. Free-wake analysis of tandem, tilt-rotor and coaxial rotor configurations[J]. Journal of the American Helicopter Society, 1996, 41(3): 196-207.

[16] 黃水林, 李春華, 徐國華. 基于自由尾跡和升力面方法的雙旋翼懸停氣動干擾計算[J]. 空氣動力學學報, 2007, 25(3): 390-395.

HUANG S L, LI C H, XU G H. An analytical method for aerodynamic interactions of twin rotors upon free-vortex and lifting-surface models[J]. Acta Aerodynamica Sinica, 2007, 25(3): 390-395 (in Chinese).

[17] SCHMAUS J, CHOPRA I. Performance and loads prediction for a high advance ratio coaxial rotor[C]∥56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston, VA: AIAA, 2015.

[18] 徐冠峰, 陳銘. 基于自由尾跡的共軸直升機航向/總距解耦分析[J]. 北京航空航天大學學報, 2011, 37(2): 249-252.

XU G F, CHEN M. Decoupling analysis between yaw and collective pitch controls of coaxial helicopter using free wake arithmetic[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(2): 249-252 (in Chinese).

[19] HO J C, YEO H, BHAGWAT M. Validation of rotorcraft comprehensive analysis performance predictions for coaxial rotors in hover[J]. Journal of the American Helicopter Society, 2017, 62(2): 1-13.

[20] JUHASZ O, SYAL M, CELI R, et al. Comparison of three coaxial aerodynamic prediction methods including validation with model test data[J]. Journal of the American Helicopter Society, 2014, 59(3): 1-14.

[21] 趙珅寧. 基于多自由度渦環單元的旋翼動態尾跡建模研究[D]. 南京：南京航空航天大學, 2016.

ZHAO K N. Research on rotor dynamic wake model based on vortex ring elements with multiple degrees of freedom [D]. Nangjing: Nanjing University of Aeronautics and Astronautics, 2016 (in Chinese).

[22] 趙珅寧, 李攀, 張亞飛, 等. 一種新的旋翼動態尾跡模型研究[J].南京航空航天大學學報, 2016, 48(2): 212-217.

ZHAO S N, LI P, ZHANG Y F, et al. Study on new rotor dynamic wake model [J]. Journal of Nanjing University of Aeronautics and Astronautics, 2016, 48(2): 212-217 (in Chinese).

[23] 王適存. 直升機空氣動力學[M]. 北京: 航空專業教材編審組, 1985.

WANG S C, Helicopter aerodynamics[M]. Beijing: Aviation Professional Educational Materials Editing Group,1985 (in Chinese).

[24] ZHAO J, HE C. A finite state dynamic wake model enhanced with vortex particle method—Derived modeling parameters for coaxial rotor simulation and analysis[J]. Journal of the American Helicopter Society, 2016, 61(2): 1-9.

[25] 鄧彥敏, 陶然, 胡繼忠. 共軸式直升機上下旋翼之間氣動干擾的風洞試驗研究[J]. 航空學報, 2003, 24(1): 10-14.

DENG Y M, TAO R, HU J Z. Experimental investigation of the aerodynamic interaction between upper and lower rotors of a coaxial helicopter[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(1):10-14 (in Chinese).

[26] 陳銘, 胡繼忠, 曹義華. 共軸雙旋翼前飛氣動特性固定尾跡分析[J]. 北京航空航天大學學報, 2004, 30(1): 74-78.

CHEN M, HU J Z, CAO Y H. Rigid-wake analysis of coaxial rotor aerodynamics in forward flight[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(1): 74-78 (in Chinese).

[27] LEI Y, BAI Y, XU Z, et al. An experimental investigation on aerodynamic performance of a coaxial rotor system with different rotor spacing and wind speed[J]. Experimental Thermal and Fluid Science, 2013, 44: 779-785.

[28] 袁野，陳仁良，李攀.共軸剛性旋翼飛行器配平特性及驗證[J]. 南京航空航天大學學報， 2016, 48(2): 186-193.

YUAN Y, CHEN R L, LI P. Trim characteristics and verification of coaxial rigid rotor aircraft[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2016, 48 (2): 186-193 (in Chinese).

[29] 辛冀, 李攀, 陳仁良. 基于三階顯式格式的旋翼時間步進自由尾跡計算與驗證[J]. 航空學報, 2013, 34(11): 2452-2463.

XIN J, LI P, CHEN R L. Prediction and validation of rotor time-marching free wake based on 3rd-oder explicit numerical scheme[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(11): 2452-2463 (in Chinese).

[30] 李攀. 旋翼非定常自由尾跡及高置信度直升機飛行力學建模研究[D]. 南京: 南京航空航天大學, 2010.

LI P. Rotor unsteady free-vortex wake model and investigation on high-fidelity modeling of helicopter flight dynamics[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010(in Chinese).

[31] 袁野, 陳仁良, 李攀,等. 共軸剛性旋翼直升機旋翼控制相位角問題分析[J]. 北京航空航天大學學報, 2017, 43(10): 2047-2053.

YUAN Y, CHEN R L, LI P, et al. Analysis on coaxial rigid rotor helicopter control phase angle [J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(10): 2047-2053(in Chinese).