高速流場中變剛度復合材料層合板顫振分析

歐陽小穗，劉毅

同濟大學 航空航天與力學學院，上海 200092

壁板顫振研究始于20世紀50年代。Miles[1]和Jordan[2]最先對壁板顫振進行了理論分析。Olson[3-4]最早用有限元法研究壁板顫振問題，分析了超聲速流中二維壁板的顫振邊界。Kouchakzadeh等[5]研究了高速流場中復合材料層合板非線性氣動彈性問題，分析了面內載荷、靜壓差、纖維方向和氣動阻尼對壁板非線性氣動彈性特性的影響。結果表明，纖維方向對板的動力學特性有明顯影響，板的非對稱特性改變了極限環振動性能。Abdel-Motaglay 等[6]針對任意方向來流對復合材料板大振幅超聲速顫振的影響提出了一種有限元公式，并對偏航超聲速流中各向同性和正交各向異性復合材料板進行了分析。Singha和Ganapathi[7]采用剪切變形有限元法研究了系統參數對復合材料層合板的超聲速顫振特性的影響。估算了臨界動壓隨板的傾斜角、纖維方向和邊界條件的變化；分析了氣動力、結構阻尼以及熱載荷對臨界動壓的影響。國內學者在復合材料壁板顫振方面也進行了系統深入的研究。王曉慶等[8]采用4節點24自由度板單元研究不同溫度場的偏航壁板顫振問題，進行了考慮偏航壁板顫振速度和壁板重量的多目標熱顫振優化設計，得到偏航壁板顫振隨溫升出現“跳躍”現象的結論。苑凱華和邱志平[9-10]采用有限元法研究了高速流場中復合材料壁板熱顫振問題，考慮結構參數不確定性對壁板顫振的影響，提出用區間描述不確定性因素估計壁板顫振臨界風速近似區間，以及發生極限環振動時的振幅變化區間，數值算例驗證了方法的有效性和可行性。楊智春等[11]采用分步求解方法研究了復合材料壁板的熱顫振，得到3種不同鋪層復合材料壁板顫振臨界速度和溫升間的關系。高揚等[12]應用有限元法研究氣流偏角和熱載荷對不同形狀復合材料壁板顫振特性的影響，分析了不同形狀復合材料壁板顫振臨界動壓隨溫升和氣流偏角的變化規律。呂秀秀等[13]研究超聲速流場中鋪層方式和鋪層方位角對復合材料層合板顫振特性的影響。

傳統的纖維增強復合材料層合板采用的是直線纖維(如圖1(a)所示)，也就是說纖維方向在單層內是不變的；隨著自動鋪放等先進制造技術的發展，利用自動鋪放設備能夠改變鋪層的纖維方向,使得纖維方向在鋪層內曲線變化(如圖1(b)所示)[14]。不同于傳統的直線纖維復合材料單層板，曲線纖維復合材料單層板中每一點的纖維方向都是不同的，隨位置變化而連續變化，單層內不同位置處的剛度也隨纖維方向的變化而變化，呈現出變剛度的特點。這種含曲線纖維鋪層的復合材料稱為變剛度復合材料。變剛度復合材料在減輕結構重量和降低制造成本等方面已顯示出優勢。

曲線纖維復合材料最早由Hyer等[15-16]提出用來代替直線纖維以提高帶孔復合材料層合板的力學性能。隨后，Gürdal等[17-20]提出了變剛度復合材料概念，研究中考慮固化過程產生的殘余熱應力等因素，結果表明，曲線纖維復合材料層合板與傳統的直線纖維復合材料相比，屈曲性能有較大提高。Wu等[21-22]采用數值方法對曲線纖維復合材料的屈曲和后屈曲性能進行了研究。杜宇等[23]采用有限元法研究了變剛度復合材料的失效性能。

迄今為止，對曲線纖維變剛度復合材料層合板力學性能的研究主要集中在屈曲問題上，而對氣動彈性問題的研究還很少。Stodieck等[24-25]研究了矩形機翼的氣動彈性性能，對曲線纖維復合材料進行了氣動彈性剪裁優化，研究表明，采用曲線纖維復合材料層合板氣動彈性性能更好，可以通過改變曲線纖維方向來提高氣動彈性穩定性，減緩突風載荷。Stodieck等[26]利用三維有限元模型對直線鋪層和曲線鋪層蒙皮的性能進行優化，評估了全尺寸氣動彈性剪裁機翼的減重能力。優化結果表明，曲線纖維的減重效果比直線纖維更好。Haddadpour和Zamani[27]將曲線纖維復合材料機翼簡化為薄壁梁進行了氣動彈性設計，對纖維方向沿展向線性變化的變剛度結構進行了最大氣動彈性失穩速度的優化。結果表明變剛度機翼的氣動彈性穩定性比傳統不變剛度的機翼要好。Stanford等[28]對低速流場中曲線纖維懸臂平板進行了氣動彈性剪裁設計，采用遺傳算法確定靜氣彈變形和顫振邊界，研究了曲線和直線纖維方向和鋪層順序對氣動彈性剪裁的影響。

本文以曲線纖維變剛度復合材料層合板為研究對象，建立變剛度復合材料壁板顫振的氣動彈性力學模型。研究高速流場中復合材料層合壁板的固有振動特性、顫振穩定性和非線性顫振響應，分析邊界條件和鋪層方式對變剛度復合材料壁板顫振特性的影響。

1 曲線纖維變剛度復合材料單層板

對圖2所示的矩形單層板，其長和寬分別為a和b，纖維方向用T0|T1表示，其中，T0為纖維在板中心處和x方向的夾角，T1為纖維在邊界(x=±a/2)處和x方向的夾角。

假設纖維方向從板的中心位置開始呈線性變化，則任意位置處纖維方位角可表示為

(1)

曲線纖維路徑為

y(x)=

(2)

2 高速流場中復合材料層合板顫振方程

對于復合材料層合板的顫振問題，考慮von-Karman非線性應變-位移關系，即

(3)

橫向剪切應變為

(4)

式中：u0和v0分別為中面上的點沿x和y方向的位移；w為z方向的位移；θx和θy分別為中面繞x軸和y軸的轉角；εm為壁板中面面內位移產生的應變；εmb為考慮大變形時，撓度在壁板中引起的面內附加應變；κ為彎曲時壁板的曲率向量；z為壁板厚度方向的坐標。

本構關系可表示為

(5)

對于層數為NL的層合板，令ε0=εm+εmb，內力表達式為

(6)

(7)

式中：A為拉伸剛度矩陣；B為耦合剛度矩陣；D為彎曲剛度矩陣；AS為剪切剛度矩陣；N、M和R分別為面內力、面內力矩和橫向剪切力。

對于曲線纖維變剛度復合材料層合板，每一點的纖維方向都是不同的，因此變剛度板的剛度不再是常量，而是隨著不同位置處纖維方位角的變化而變化。采用有限元法分析時，需要通過增加網格密度來模擬由于纖維方位角的變化而帶來的剛度變化，才能保證分析結果的精度。

對高速流場(Ma>1.6)中的壁板顫振，可由一階準定常活塞理論計算氣動力，壁板表面氣流沿x方向時，有

(8)

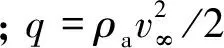
由虛功原理可得高速流場中壁板的運動方程為

(9)

式中：w為位移向量；M為質量矩陣；C為氣動阻尼矩陣；Ka為氣動剛度矩陣；KL為線彈性剛度矩陣；N1和N2為大變形產生的非線性剛度矩陣。

高速流場中考慮幾何非線性的壁板顫振方程采用Newmark法求解。

為便于后續分析，對壁板顫振動壓和頻率等參數進行無量綱化，無量綱動壓λ和無量綱頻率ω*分別為[29]

(10)

式中：D=E2t3，E2為橫向彈性模量，t為板的厚度；ρ為板的密度；ω為振動頻率。

(11)

式中：W為無量綱振幅；x和y為坐標值。

3 算法驗證

3.1 正確性驗證

用文獻[30]中的四邊簡支碳/環氧復合材料層合板對本文算法及程序的正確性進行驗證。材料屬性如表1所示，板的尺寸a=b=0.305 m，板厚為1.27 mm，鋪層為[0/45/-45/90]s。采用考慮橫向剪切的3節點Mindlin(MIN3)板單元進行有限元分析，整個板用10×10的網格表示，共劃分為200個MIN3板單元。分析結果與文獻[30]的結果對比如圖3所示。可以看出本文結果與文獻[30]的結果吻合較好。

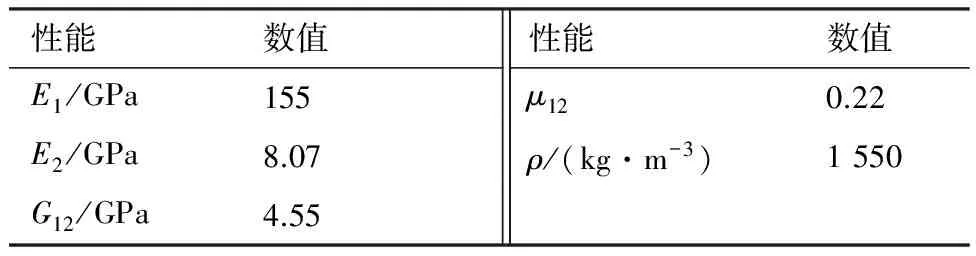
表1 復合材料層合壁板材料性能Table1 Material properties of composite laminates

3.2 網格收斂性研究

考慮四邊固支曲線纖維變剛度復合材料層合壁板，其材料屬性見表1。幾何尺寸為a×b=0.2 m×0.3 m，單層厚度為0.15 mm，鋪層為 [0/90/T0|T1/-T0|-T1]s，來流方向平行于x軸。采用有限元法進行分析，單元為考慮橫向剪切的3節點Mindlin(MIN3)板單元。

表2 曲線纖維復合材料層合板無量綱顫振動壓網格收斂性Table 2 Mesh convergence of non-dimensional flutter dynamic pressure of composite laminates with curvilinear fibers

注：表中的誤差以網格100×100為基準進行計算。

綜合考慮非線性壁板顫振的計算精度和效率，本文后續計算采用32×15共960個MIN3板單元的網格劃分。

4 復合材料層合板顫振穩定性分析

4.1 動力學特性分析

考慮到壁板的動力學特性與顫振特性有密切關系，首先對層合復合材料壁板的固有振動特性進行分析。

計算不同鋪層曲線和直線纖維復合材料層合板動力學特性。對[0/90/T0|T1/-T0|-T1]s，考慮T0=0°～45°、T1=45°和T0=45°、T1=45°～90°這2種情況，前6階固有頻率計算結果分別如表3和表4所示。

從表3和表4可以看出，T0和T1對曲線纖維復合材料層合壁板的固有頻率均有一定影響。當T1相同而T0不同時，1、4和5階固有頻率隨T0增大而減小，而2、3和6階固有頻率隨T0的增大而增大。當T0相同而T1不同時，1、2、4和5階頻率隨T1增大而減小，而3階和6階固有頻率隨T1增大而增大。這是由于變剛度復合材料層合板內纖維方向的變化而導致剛度不再是常量，而是隨著位置的變化而變化引起的。利用這一特點，可以通過調整纖維方向改變復合材料層合壁板的固有振動特性。

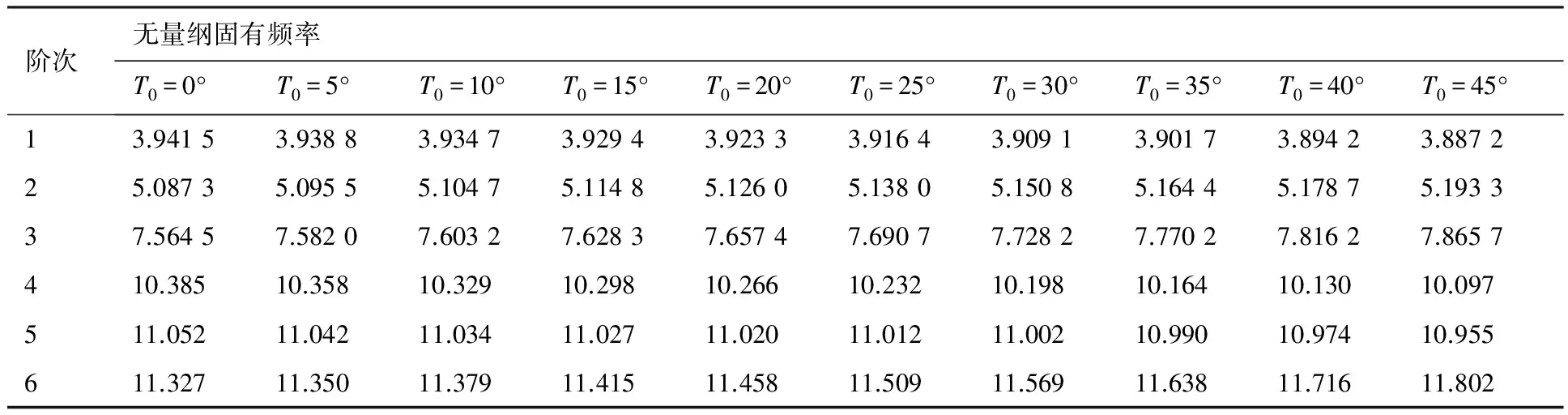
表3 曲線纖維復合材料層合板無量綱固有頻率隨T0的變化(T1=45°)Table 3 Non-dimensional natural frequency of composite laminates with curvilinear fibers with various T0 (T1=45°)

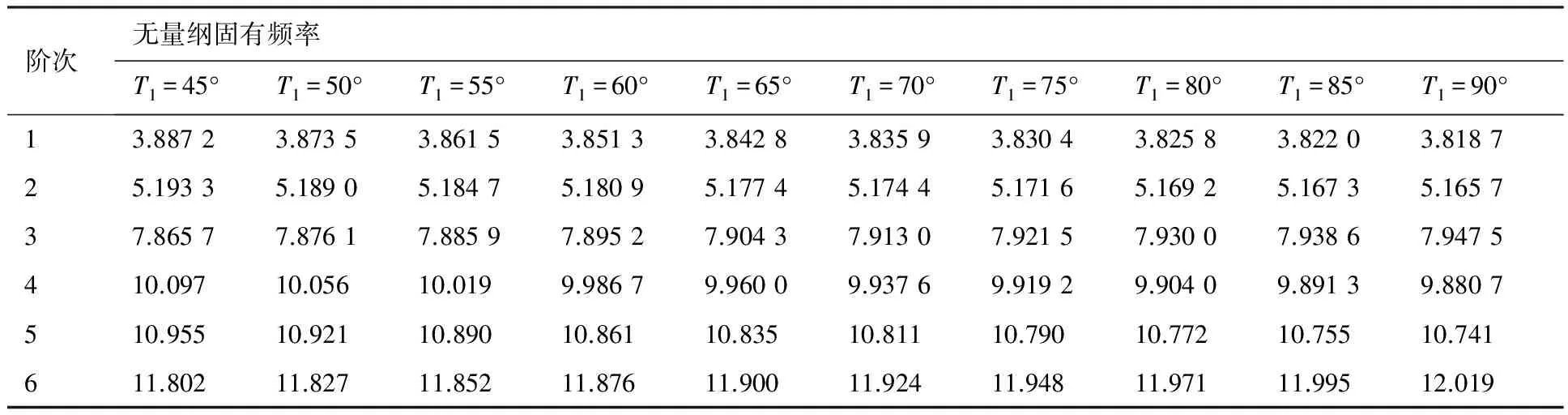
表4 曲線纖維復合材料層合板無量綱固有頻率隨T1的變化(T0=45°)Table 4 Non-dimensional natural frequency of composite laminates with curvilinear fibers with various T1 (T0=45°)

4.2 模態耦合分析

對不同鋪層曲線和直線纖維復合材料層合板耦合模態進行計算。考慮5種曲線纖維和1種直線纖維層合板，鋪層分別取 [0/90/0|15/0|-15]s、[0/90/0|30/0|-30]s、[0/90/0|45/0|-45]s、 [0/90/15|45/-15|-45]s、[0/90/30|45/-30|-45]s和[0/90/±45]s，耦合模態分析結果如圖4所示。以[0/90/0|45/0|-45]s和[0/90/±45]s為例進行耦合特性分析，其模態如圖5所示。可以看出，當T0相同而T1不同或者當T1相同而T0不同時，顫振均由1階模態和4階模態耦合引起。即對上述層合板，耦合模態與T0和T1無關。

4.3 邊界條件的影響

對不同邊界條件下曲線纖維和直線纖維復合材料層合板顫振特性進行計算。考慮6種不同鋪層曲線纖維和1種直線纖維層合板，鋪層分別取 [0/90/0|45/0|-45]s、[0/90/15|45/-15|-45]s、[0/90/30|45/-30|-45]s、[0/90/45|60/-45|-60]s、[0/90/45|75/-45|-75]s、[0/90/45|90/-45|-90]s和[0/90/±45]s，馬赫數為3，四邊簡支和四邊固支下的計算結果如圖6所示。可以看出，邊界約束越強，層合板的穩定性越好，顫振臨界動壓越大。無論是直線纖維還是曲線纖維，四邊固支層合板的顫振臨界動壓均明顯高于四邊簡支層合板。

4.4 曲線纖維方向的影響

計算不同鋪層曲線纖維和直線纖維復合材料層合板顫振特性。對[0/90/T0|T1/-T0|-T1]s，考慮T1不變、T0=-90°～90°和T0不變、T1=-90°～90°這2種情況，馬赫數取3，計算結果如圖7所示。

可以看出，T0和T1對曲線纖維復合材料層合壁板的顫振均有一定影響。T1不變時，顫振臨界動壓隨T0的變化規律一致。當纖維方向逼近x方向時顫振臨界動壓增加，這是由于層合板x方向的剛度增加。T0不變、T1變化時的變化規律與T1不變、T0變化的情況相同。當T0=T1=0°時，層合板x方向的剛度最大，顫振臨界動壓達到最大值。可見，通過調整曲線纖維的路徑可以改變曲線纖維復合材料層合壁板的顫振臨界動壓。

5 變剛度復合材料層合板的非線性顫振

5.1 變剛度復合材料層合板的非線性顫振響應

高速流場中曲線纖維變剛度復合材料層合板在給定初始擾動下，若在顫振臨界動壓以下,層合板的運動隨時間減小，則響應是收斂的；當超過臨界動壓，層合板的振幅隨時間增大直到最大振幅，則形成極限環振動。圖8和圖9分別表示[0/90/±45]s和[0/90/0|45/0|-45]s復合材料層合板的顫振時間歷程和相平面圖(所取點位于 (0.75a, 0.5b)處)。從圖8可以看出，對傳統的直線纖維層合板[0/90/±45]s，當λ=510時，壁板受到初始擾動后，振動是收斂的，表明動壓未達到顫振臨界動壓；當λ=520時，壁板受到初始擾動后，處于極限環振動，此時動壓超過顫振臨界動壓，層合板做周期振動，出現顫振。從圖9可以看出，對曲線纖維層合板[0/90/0|45/0|-45]s；當λ=550時，壁板受到初始擾動后，隨著時間的增加振動是收斂的，表明動壓未達到顫振臨界動壓；當λ=560時，壁板受到初始擾動后，處于極限環振動，此時動壓超過顫振臨界動壓，層合板做周期振動，出現顫振。圖10表示t=0.255 s時，[0/90/±45]s和[0/90/0|45/0|-45]s這2種層合板的極限環顫振變形，最大值出現在(0.75a, 0.5b)處。

5.2 曲線纖維方向對非線性顫振響應的影響

對不同鋪層的曲線纖維和直線纖維復合材料層合板非線性顫振進行分析。鋪層為[0/90/T0|T1/-T0|-T1]s，考慮T0=0°～45°、T1=45°和T0=45°、T1=45°～90°這2種情況，馬赫數取3。T0和T1對振幅的影響如圖11所示。

可以看出，T0和T1對曲線纖維復合材料層合壁板的顫振均有一定影響。當T1相同而T0不同時，壁板的極限環振幅隨T0的增大而增大；當纖維T0相同而T1不同時，壁板的極限環振幅隨T1增大而增大。

圖12表示不同鋪層的變剛度復合材料層合板在不同邊界條件時，顫振幅值隨動壓的變化。可以看出不同鋪層和不同邊界條件下的顫振幅值隨動壓的變化趨勢基本一致，極限環振幅隨動壓的增加而增大。不同邊界條件下，由于復合材料不同方向的剛度影響，壁板的振幅隨T0或T1的增加而增大。固支情況下，T0和T1對振幅的影響更大。

6 結 論

1)T0和T1對曲線纖維復合材料層合壁板的固有振動特性有一定影響，可以通過調整T0和T1改變壁板的固有振動特性。

2)T0或T1對曲線纖維復合材料層合壁板顫振耦合模態的影響不大。

3) 邊界條件對復合材料層合壁板的顫振臨界動壓有較大影響，邊界約束越強，壁板的穩定性越好，顫振臨界動壓越大。

4)T0和T1對壁板的顫振臨界動壓有較大影響，隨著T0或T1的增大，顫振臨界動壓減小。

5) 直線纖維鋪層和曲線纖維鋪層的顫振極限環變形最大值都出現在(0.75a, 0.5b)處。

6) 相同的動壓下，隨著T0或T1的增大，曲線纖維復合材料層合板的極限環振幅增大。

7) 曲線纖維復合材料層合壁板顫振幅值隨動壓的變化趨勢基本一致，極限環振幅隨動壓的增加而增大，且固支條件下T0和T1對振幅的影響更大。

綜上所述，高速流場中，邊界條件對曲線纖維復合材料層合壁板的非線性顫振特性有明顯影響，采用曲線鋪層可根據需要調整壁板的非線性顫振特性，進一步提高復合材料的可設計性。

參 考 文 獻

[1] MILES J W. Dynamic chordwise stability at supersonic speeds： Report AL-1140[R]. Dundalk, MD: North American Aviation, Inc., 1950.

[2] JORDAN P F. The physical nature of panel flutter[J]. Aero Digest, 1956, 72(2): 34-38.

[3] OLSON M D. Finite elements applied to panel flutter[J]. AIAA Journal, 1967, 5(12): 2267-2270.

[4] OLSON M D. Some flutter solutions using finite elements[J]. AIAA Journal, 1970, 8(4): 747-752.

[5] KOUCHAKZADEH M A, RASEKH M, HADDADPOUR H. Panel flutter analysis of general laminated composite plates[J]. Composite Structures, 2010, 92(12): 2906-2915.

[6] ABDEL-MOTAGLAY K, CHEN R, MEI C. Nonlinear flutter of composite panels under yawed supersonic flow using finite elements[J]. AIAA Journal, 1999, 37(9): 1025-1032.

[7] SINGHA M K, GANAPATHI M. A parametric study on supersonic flutter behavior of laminated composite skew flat panels[J]. Composite Structures, 2005, 69(1): 55-63.

[8] 王曉慶, 韓景龍, 張軍紅. 不同氣流偏角下的壁板熱顫振分析及多目標優化設計[J]. 航空學報, 2010, 31(11): 2195-2201.

WANG X Q, HAN J L, ZHANG J H. Thermal flutter analysis of panel and multi-objective optimization design considering variation of flow yaw angle[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(11): 2195-2201 (in Chinese).

[9] 苑凱華, 邱志平. 含不確定參數的復合材料壁板熱顫振分析[J]. 航空學報, 2010, 31(1): 119-124.

YUAN K H, QIU Z P. Thermal flutter analysis of composite panel with uncertain parameters[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(1): 119-124 (in Chinese).

[10] 苑凱華, 邱志平. 高超聲速氣流中復合材料壁板熱顫振分析[J]. 南京航空航天大學學報, 2010, 42(3): 313-317.

YUAN K H, QIU Z P. Flutter analysis of composite panels in hypersonic flow with thermaleffects[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(3): 313-317 (in Chinese).

[11] 楊智春, 譚光輝, 夏巍. 鋪層方式對復合材料壁板熱顫振特性的影響[J]. 宇航學報, 2008, 29(3): 1047-1052.

YANG Z C, TANG G H, XIA W. Thermal flutter analysis of composite panel with uncertain parameters[J]. Journal of Astronautics, 2008, 29(3): 1047-1052 (in Chinese).

[12] 高揚, 楊智春, 谷迎松. 氣流偏角對不同形狀復合材料壁板熱顫振特性的影響[J]. 振動與沖擊, 2014, 33(11): 65-69.

GAO Y, YANG Z C, GU Y S. Effects of flow yaw angle on thermal flutter characteristics of composite panels with differentshapes[J]. Journal of Vibration and Shock, 2014, 33(11): 65-69 (in Chinese).

[13] 呂秀秀, 李鳳明, 宋智廣. 超聲速復合材料層合壁板結構的顫振特性分析[J]. 計算力學學報, 2013, 30(S1): 140-143.

LV X X, LI F M, SONG Z G. Flutter characteristic analysis of supersonic composite laminated panel[J]. Chinese Journal of Computational Mechanics, 2013, 30(S1): 140-143 (in Chinese).

[14] AKHAVAN H, RIBEIRO P. Natural modes of vibration of variable stiffness composite laminates with curvilinear fibers[J]. Composite Structures, 2011, 93(11): 3040-3047.

[15] HYER M W, CHARETTE R F. Use of curvilinear fiber format in composite structure design[J]. AIAA Journal, 1991, 29(6): 1011-1015.

[16] HYER M W， LEE H H. The use of curvilinear fiber format to improve buckling resistance of composite plates with central holes[J]. Composite Structures, 1991, 18(3): 239-261.

[17] GüRDAL Z, OLMEDO R. In-plane response of laminates with spatially varying fiber orientations: Variable stiffness concept[J]. AIAA Journal, 1993, 31(4): 751-758.

[18] LOPES C S, CAMANHO P P, GüRDAL Z, et al. Progressive failure analysis of tow-placed, variable-stiffness composite panels[J]. International Journal of Solids and Structures, 2007, 44(25-26): 8493-8516.

[19] GüRDAL Z, TATTING B F, WU C K. Variable-stiffness composite panels: Effects of stiffness variation on the in-plane and buckling response[J]. Composites: Part A, 2008, 39(5): 911-922.

[20] LOPES C S, GüRDAL Z, CAMANHO P P. Variable-stiffness composite panels: Buckling and first-ply failure improvements over straight-fiber laminates[J]. Computers and Structures, 2008, 86(9): 897-907.

[21] WU Z, WEAVER P M, RAJU G, et al. Buckling analysis and optimisation of variable angle tow composite plates[J]. Thin-Walled Structures, 2012, 60(10): 63-172.

[22] WU Z, RAJU G, WEAVER P M. Postbuckling analysis of variable angle tow composite plates[J]. International Journal of Solids and Structures, 2013, 50(10): 1770-1780.

[23] 杜宇, 楊濤, 李志猛, 等. 纖維曲線鋪放的變剛度復合材料層合板的失效分析[J]. 宇航材料工藝, 2013, 43(5): 22-25.

DU Y, YANG T, LI Z M, et al. Failure analysis of variable-stiffness composite laminates with curvilinear fiber placement[J]. Aerospace Materials & Technology, 2013, 43(5): 22-25 (in Chinese).

[24] STODIECK O, COOPER J E, WEAVER P M, et al. Improved aeroelastic tailoring using tow-steered composites[J]. Composite Structures, 2013, 106: 703-715.

[25] STODIECK O, COOPER J E, WEAVER P M. Optimization of tow-steered composite wing laminates for aeroelastic tailoring[J]. AIAA Journal, 2015, 53(8): 2203-2215.

[26] STODIECK O, COOPER J E, WEAVER P M. Aeroelastic tailoring of a representative wing box using tow-steered composites[J]. AIAA Journal, 2017, 55(4): 1425-1439.

[27] HADDADPOUR H, ZAMANI Z. Curvilinear fiber optimization tools for aeroelastic design of composite wings[J]. Journal of Fluids and Structures, 2012, 33(5): 180-190.

[28] STANFORD B K, JUTTE C V, WU K C. Aeroelastic benefits of tow steering for composite plates[J]. Composite Structures, 2014, 118: 416-422.

[29] PIDAPARTI R M V, YANG H T Y.Supersonic flutter analysis of composite plates and shells[J]. AIAA Journal, 1993, 31(6): 1109-1117.

[30] ZHOU R C, XUE D Y, MEI C. Finite element time domain-modal formulation for nonlinear flutter of composite panels[J]. AIAA Journal, 1994, 32(10): 2044-2052.