基于超網格的重疊網格守恒插值方法

崔鵬程，唐靜，李彬，馬明生，鄧有奇

中國空氣動力研究與發展中心 計算空氣動力研究所， 綿陽 621000

在多體分離、艙門開啟、返回艙降落與螺旋槳滑流等非定常流動模擬中，常采用重疊網格方法，將復雜的流動區域劃分為多個簡單的子區域，各子區域內的網格獨立生成，數值計算在各個子網格上獨立進行，各子網格之間存在重疊關系，流場信息通過插值在重疊區域進行匹配和耦合[1]。重疊網格方法降低了網格生成難度，在多體相對運動數值計算方面具有很多優勢，但各子網格間的數據插值很難保證守恒性[2]。

重疊網格間高精度插值是保證流場計算正確的重要基礎，目前主要有兩種插值方法：守恒插值和非守恒插值。非守恒插值方法實現簡單，處理無間斷流動時插值精度較高，對此國內外很多學者開展了大量的研究工作。田書玲等[3-4]對物理空間的曲面單元進行了標準化處理，實現了基于非結構動態網格的Lagrange插值方法；Marstin和Mcconnaughey[5]利用有限元思想構造空間標準單元的線性插值函數，研究了雙線性、三線性重疊網格插值方法；康忠良等[6]基于線性重構思想，發展了一種適用于任意單元的重疊網格插值策略，黃宇等[7]按單元尺度區分和擴充貢獻單元模板，改善了網格尺寸相差較大時的插值精度；周乃春等[8]采用逆向距離權方法對重疊網格邊界的物理量進行插值。

但非守恒插值方法對網格的相對尺寸依賴性較強，在網格尺寸相差較大的區域插值精度較低，且不能實現物理量在插值區域的守恒性，在非定常數值計算中可能會引起非物理擾動，此外，非守恒方法即使計算網格質量很好，也會使速度的計算值在重疊網格邊界之間產生錯位[1,9]。

守恒插值方法精度較高，能實現物理量在插值區域的守恒性，對網格相對尺寸依賴性較小，但過程處理復雜，實現相對困難。常見的守恒插值方法有嵌入網格方法[10]、分段交界面方法[11]、ENO(Essentially Non Oscillatory)守恒重映方法[12]和總體守恒隱式插值方法[13]等。其中嵌入網格方法和分段交界面方法都是在幾何上將不重合邊界轉化為重合邊界，在三維情況下較難實現，ENO守恒重映方法需分解幾何單元，構造幾何單元之間的面相交問題比較復雜，總體守恒隱式插值方法雖然計算精度較高，但需要求解附加方程組，給并行計算增添了難度。

Farrell和Maddison[14]發展了一種新的插值方法，提出“超網格”思想，構造了二維網格的積分守恒插值，2011年文獻[15]進一步發展了三維多面體的切割算法。徐春光等[16]發展了二維/三維混合網格下的單元相交算法，實現了二階精度的守恒插值方法。

本文在Farrell[14]、Menon[15]和徐春光[16]等的基礎上，基于“超網格”思想與單元相交算法，發展了一種適用于非定常數值計算的隱式并行混合重疊網格守恒插值方法，在每一個非定常時間步內構造局部超網格，利用局部超網格實現背景網格向目標網格的守恒插值。經過數值試驗驗證，對于二階分布的流場變量，該方法在重疊網格區域可以保證嚴格守恒插值，加快殘差收斂速度，提高流場變量的插值精度。

1 數值方法

1.1 控制方程

雷諾平均Navier-Stokes方程守恒形式的積分方程為

(1)

式中:W=[ρρuρvρwρE]T為守恒流場變量,ρ為密度,u、v、w為速度分量，E為能量；V為體積分;S為面積分；Ω為重疊區域;Hc為對流通量；Hv為黏性通量；n為流動區域邊界上指向外側的單位法向量。

本文使用的流場解算器為自主研發的MFlow軟件[17]，對流通量和黏性通量的具體內容可以參考文獻[18]，控制方程的離散采用格心格式的有限體積法，時間項采用LU-SGS(Lower-Upper Symmetric Gauss-Seidel)迭代[19]，湍流模型為一方程Spalart-Allmaras(S-A)模型[20]。黏性項采用中心格式，對流項采用Roe格式[21]，非定常計算過程采用多重網格加速收斂[22]。

1.2 積分型守恒插值條件

本文以兩套重疊子網格為例，簡要說明重疊網格守恒插值方法。在守恒插值過程中要求守恒量的積分值保持恒定。

重疊子網格為ΓA、ΓB，重疊區域為Ω，設ΓA為背景網格，ΓB為插值網格，qA(x)為守恒變量在ΓA的分布函數，qB(x)為守恒變量在ΓB的分布函數，ΠAB為ΓA插值到ΓB的插值算子，如果滿足方程：

(2)

則稱qB(x)是qA(x)的守恒插值，其中qB(x)=qA(x)ΠAB。

2 超網格構造方法

2.1 超網格定義

“超網格”概念最早由Farrell和Maddison提出[14]。對于任意兩套網格ΓA、ΓB，重疊區域為Ω，NA、NB分別為其網格節點，EA、EB分別為網格邊，K∈Γ為網格單元。由{ΓA,ΓB}組成的超網格ΓC滿足以下條件：

1)NC?NA∪NB。

2)V(KC∩K)∈{0,V(KC)}?KC∈ΓC,

K∈Γ,Γ∈{ΓA,ΓB}。

即在ΓA、ΓB重疊區域內，超網格的網格節點必須包含ΓA、ΓB所有的節點，且超網格ΓC的每一個網格單元KC與ΓA、ΓB網格單元的相交體體積為零或為KC的體積，超網格的每個網格單元總是包含于ΓA或ΓB的網格單元。

2.2 局部超網格構造

按照2.1節中超網格定義，任意兩套網格ΓA、ΓB的所有網格節點及邊可組成它們的超網格ΓC[15]。圖1為文獻[15]給出的超網格示意圖，圖中a～e為網格節點。將目標網格ΓB的每一個網格單元與背景網格ΓA的網格單元求交，求交得到的網格單元可構成ΓA、ΓB的超網格，母網格ΓA、ΓB的每一個網格單元總是可以拆分為一個或多個超網格單元的集合。

文獻[15]給出了全局超網格的構造方法，即背景網格ΓA與目標網格ΓB完全重合，所得超網格ΓC也與ΓA、ΓB完全重合。在重疊網格中各子網格區域不可能完全重合，且在非定常數值模擬中各子網格位置會相對變化。本文提出一種適用于重疊網格非定常數值模擬的局部超網格構造方法，在每一個非定常時間步內構造局部超網格，利用局部超網格實現背景網格向目標網格的守恒插值。局部超網格構造方法如下：

1) 在重疊網格各子網格之間進行挖洞操作，標識出各子網內不需要計算的網格、計算網格和插值網格等。

2) 用ADT(Alternating Digital Tree)搜索方法求出子網格每一個插值單元的所有貢獻單元[23]。普通的插值方法中一個插值單元只需用到一個貢獻單元信息，但在基于超網格的守恒插值方法中，一個插值單元需用到多個貢獻單元的信息。

構造局部超網格需搜索出所有與插值單元相交的貢獻單元，圖2給出了搜索貢獻單元的示意圖，首先用ADT搜索方法快速定位插值單元的體心在背景網格的位置，體心所在的單元為1個貢獻單元，如圖2(a)所示；然后以此貢獻單元為基礎，檢索所有與此單元共點的背景網格，搜索出與插值網格相交的網格單元，這些單元也是貢獻單元；重復檢索與貢獻單元共點的網格單元，當所有與貢獻單元共點的網格都不與插值單元相交時，終止搜索，如圖2(b)所示。

3) 求出重疊網格子網格的插值單元與其每一個貢獻單元的相交多面體，相交多面體可構成局部超網格。

4) 以局部超網格為媒介，在每一步內迭代計算中實現貢獻單元向插值單元的守恒插值。當前時間步計算結束時，釋放超網格。下一個時間步開始計算時，根據當前子網格的相對位置重新建立超網格。

2.3 網格求交算法

由2.2節可知，插值單元與貢獻單元求交是獲取超網格的關鍵，不同的網格單元有不同的網格求交算法。對凸多邊形或多面體而言，二維和三維網格求交方法已經較為成熟[24]，本文采用快捷的Sutherland-Hodgman 逐邊切割方法[16,25]。

Sutherland-Hodgman方法的基本思想為用切割多邊形的各邊界線逐次對目標多邊形進行切割，從而得到一個新的多邊形。圖3為Suther-land-Hodgman方法示意圖，以兩個二維多邊形求交為例，三角形A1A2A3與B1B2B3求交。把A1A2A3當做目標三角形，B1B2B3當做切割三角形。用B1B2B3的各條邊依次對A1A2A3進行切割，得到相交多邊形B1CDEF。

三維情況下Sutherland-Hodgman方法的思想為用切割多面體的各個面逐次對目標多面體進行切割，從而形成一個新的多面體。在三維數值模擬中，常見的網格單元包括四面體、三棱柱、金字塔和六面體等單元。其中三棱柱、金字塔和六面體單元具有四邊形表面。在用常見的Pointwise、Icem等商業軟件生成網格的過程中，為了提高物面網格投影的精度和空間網格的光滑性，會對網格進行扭轉或彎曲變形，從而導致四邊形的4個頂點不能嚴格地分布在同一平面內，在多面體切割的過程中會產生歧義[26]。為了消除歧義，在多面體求交時，首先將三棱柱、金字塔和六面體單元分解為多個小四面體單元。通過小四面體相交體的組合來實現多面體求交。圖4所示為四面體網格求交算法，四面體P1與P2求交，將P2當做目標四面體，P1當做切割四面體，用P1的各個面對P2進行切割，保留切割面內側的交點與交線，從而獲得P1、P2的相交體P3。相比平面多邊形而言，四面體求交得到的多面體構造比較復雜，圖4中四面體P1、P2的相交體P3是具有10個頂點的7面體。

圖5所示為用網格求交方法構造三維超網格的方法，具體步驟如下：

1) 在獲取重疊網格局部超網格時，先用ADT搜索方法求出子網格每一個插值單元的所有貢獻單元。在三維情況下，一個插值單元可能有多個對應的貢獻單元，圖5(a)為一個插值單元與其相交的背景單元，這個插值單元有2個貢獻單元。

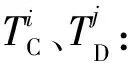
(3)

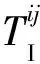
(4)

則插值單元PC與貢獻單元PD的相交體PI可表示為小四面體交集的并集：

(5)

其體積VI與體心XI分別為

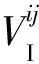
(6)

3) 插值單元與貢獻單元的相交體可組成局部超網格，圖5(b)為一個插值單元與其超網格，每一個超網格單元都由插值單元與其貢獻單元相交獲得。

3 基于超網格的守恒插值方法

3.1 積分轉換

本文使用的流場計算器MFlow軟件控制方程的離散采用格心格式的有限體積法，流場數據儲存在網格體心處，網格K的體積為VK，其體心XK可以表示為

(7)

與式(6)類似，對于任意的多面體網格，其體積和體心都可以分解為四面體來計算，即

VK=∑Vi

(8)

式中：Vi和Xi分別為四面體的體積與體心。

一般流體計算中認為流場變量呈二階分布，將流場變量Taylor展開：

(9)

可以證明，流場變量在K單元的平均值就等于體心值，流場變量在K單元的積分值等于體心值與體積的乘積,即

qK

(10)

3.2 守恒插值方法

以超網格為媒介，可以實現重疊網格子網格之間的守恒插值，具體方法如下。

式(2)是重疊網格守恒插值條件，將其在背景網格ΓA、插值網格ΓB上離散化，即

(11)

根據超網格的特點，插值網格ΓA的每一個網格單元KB總是可以拆分為一個或多個超網格單元的集合，設ΓC為其超網格，網格單元為KC，則式(11)可寫為[15]

(12)

這樣就把ΓA到ΓB的守恒插值轉換到ΓA到ΓC的守恒插值。根據超網格的特點，背景網格ΓA的每一個網格單元KA總是可以拆分為一個或多個超網格單元的集合。超網格單元KC的體積為VKC，則其體心XKC可表示為

(13)

設KC為貢獻單元KA所包含的一個超網格單元，可以利用二階Taylor重構[6,27-28]將任意變量插值從貢獻單元體心XKA插值到超網格體心XKC處，即

(14)

設貢獻單元KA包含m個超網格，可以證明通過式(9)的插值方式，變量q在KA上的積分可寫為在KA所包含的m個超網格上的積分之和，即

(15)

綜合式(11)、式(12) 、式(15)，背景網格ΓA的流場變量可通過超網格ΓC插值到插值網格ΓB，即

(16)

式(15)整個插值過程對二階分布的流場變量嚴格守恒，具體實現過程總結如下：

1) 將流場變量從貢獻單元KA插值到它的超網格單元KC，即

(17)

2) 將超網格ΓC的流場變量采用體積權插值到插值單元KB，設KB包含n個超網格單元KC，則其流場變量q(XKB)可寫為

(18)

這樣以超網格為媒介，將流場變量從貢獻單元KA插值到插值單元KB。如果流場變量q(x)二階分布，則整個插值過程嚴格守恒，這種插值方法不會改變原先流場的二階分布，實現了超網格單元和插值單元流場變量的精確守恒插值。

3.3 隱式并行插值方法

在重疊網格插值過程中，根據貢獻單元是否同時也是插值單元，插值方法可分為隱式插值和顯式插值。顯式插值方法需區分背景網格與插值網格，插值速度較慢，不適合復雜構型的大規模重疊網格。本文發展了一種隱式并行插值方法，不嚴格區分背景網格與插值網格，如圖6所示，每一套網格既向其他網格發送數據，同時又從其他網格接收數據。

這種隱式并行的重疊網格插值方法插值速度較快，適用于多個相對運動的子網格間的流場數據插值，能處理復雜構型的大規模重疊網格。

4 算例分析

本文首先采用不同類型的流場方程對所建立的插值方法的守恒性和插值精度進行驗證。然后將該方法用于CFD重疊網格標模的數值模擬，通過跟試驗數據對比，考核該方法的魯棒性和工程實用性。

4.1 守恒性驗證

4.1.1 線性方程

假設物理量φ在網格區域線性分布，滿足方程：

φ(x,y,z)=2x+3y+z

(19)

如圖7所示，ΓA、ΓB分別為結構與非結構四面體網格，網格區域一致。在網格上設定物理量φ的分布滿足式(19)，然后ΓA、ΓB間進行100次相互插值，統計φ在ΓB網格區域內的積分值與每個單元的平均插值誤差絕對值。

圖8對比了本文插值方法與三線性插值方法、逆向距離權插值方法在守恒性和插值精度上的異同。圖8(a)為φ在ΓB網格區域內的積分值，可以看出用本文守恒插值方法計算得出的積分值在插值過程中保持恒定，按照式(11)守恒插值的定義，該方法在計算過程中可保持物理量積分的嚴格守恒。而三線性插值方法和逆向距離權插值方法不具備守恒性，且隨著插值次數的增加，物理量積分值與理論值的誤差越來越大。

圖8(b)為φ在ΓB網格區域內每個單元的平均插值誤差絕對值，可以看出與三線性插值方法和逆向距離權插值方法相比，本文所建立的插值方法插值精度更高。

4.1.2 三角函數

假設物理量φ在網格區域呈三角函數分布，滿足方程：

φ(x,y,z)=1+sin(2πx)sin(2πy)sin(2πz)

(20)

插值網格與計算條件同4.1.1小節。圖9對比了三角函數的插值過程中，本文插值方法與三線性插值方法、逆向距離權插值方法在守恒性和插值精度的異同。可以看出，本文發展的守恒插值方法對三角函數的插值計算具有較強的守恒性(見圖9(a))，且插值精度明顯高于三線性插值方法與逆向距離權插值方法(見圖9(b))。

4.2 定常數值計算

4.2.1 ONERA-M6機翼

將重疊網格數值計算結果與單套整體網格數值計算結果對比是一種常用的檢驗重疊網格技術優劣的方法[7,23]。為了考察本文重疊網格插值方法的插值精度，對ONERA-M6機翼分別采用非結構重疊網格與單套整體網格進行數值模擬，計算來流條件為:馬赫數Ma=0.84, 迎角α=3.06°, 來流溫度T∞=255.56 K, 雷諾數Re=1.172×107。

重疊網格由兩部分組成：背景網格和機翼網格，機翼表面采用各向異性網格對機翼前后緣進行加密，機翼近壁面采用三棱柱網格以較好地模擬黏性，遠壁面采用四面體、金字塔和六面體的混合網格，機翼網格量約為60.3萬。背景網格全部采用四面體網格單元，網格量約為6.1萬。兩套子網格的重疊效果如圖10所示，總網格量為66.4萬。

單套全機網格的近壁面網格分布與重疊網格完全一致，空間網格尺度和網格數量與兩套重疊網格相當，總網格量為54.8萬。

如圖11(a)和圖11(b)所示，本文將不同重疊網格插值方法的壓力系數Cp計算結果與相同網格尺度單套整體網格的計算結果進行對比，可以看出相比三線性插值方法與逆向距離權插值方法，本文所提出的插值方法計算得出的壓力系數和單套整體網格的計算結果更為符合,其中L為機翼展長。由于本文建立的插值方法提高了重疊網格交界面的插值精度，使得激波附近的壓力系數計算更為精確。

從圖11(a)和圖11(b)可以發現CFD計算結果與風洞試驗結果符合良好，前緣吸力峰和激波位置與風洞試驗數據較為一致。但仔細對比發現，整體網格與守恒插值方法計算得出的Cp與試驗值略有偏差。ONERA-M6機翼是一個跨聲速機翼，如圖11(c)和圖11(d)所示，大量的數值計算[29-33]表明，對于ONERA-M6機翼跨聲速狀態，全局加密網格、S-A模型、DES和DDES方法的數值計算結果都無法與風洞試驗完全符合，這是數值計算和風洞試驗的固有偏差[29-30]。而三線性與距離權插值方法在激波后部與風洞試驗完全符合，這是完全不合理的，也恰好說明這兩種重疊網格插值方法數值誤差較大。本文建立的守恒插值方法計算結果與整體網格、文獻[29-33]一致，說明該方法插值精度較高，產生的數值誤差較小。

圖12給出了用不同重疊網格插值方法計算的殘差收斂曲線，可以看出由于本文守恒插值方法在重疊網格區域插值精度較高，引入誤差較小，使得收斂速度較快。本文插值方法的收斂速度分別比逆向距離權方法和三線性方法快20.0%和10.8%。

4.2.2 NACA0012翼型激波干擾

取2個并列錯位的NACA0012翼型進行超聲速擾流計算，來流條件為:Ma=2,α=0°,Re=1.812×107。

在此計算條件下，由于翼型并列錯位，2個翼型之間會產生強烈的激波干擾，流場結構比較復雜，本文采用重疊網格對此算例進行數值模擬，如圖13所示,重疊網格由兩部分組成：上翼型網格和下翼型網格。

為了考核插值方法在重疊網格邊界的插值精度，人為地將計算網格分布得較為稀疏，在重疊網格邊界,網格的尺度相差較大。

圖14(a)～圖14(c)給出了不同插值方法計算得到的馬赫數等值線分布，白色、黑色分別為上、下翼型網格的馬赫數等值線，圖14(d)為細網格計算結果，3種插值方法都正確模擬了流場結構。可以看出，在上下翼型重疊網格交界面附近，用三線性和逆向距離權插值方法計算得到的馬赫數等值線有明顯的錯位，而守恒插值方法得到的馬赫數等值線較為光滑。在下面翼型的尾流區域，人為設置了兩套子網格的尺度，使得在重疊網格邊界兩套網格的尺度相差較大，在這種情況下，三線性和逆向距離權插值方法計算得到的等值線出現了明顯的間斷，而守恒插值方法得到的馬赫數等值線仍然較為連續。此外，2個NACA0012翼型并列錯位，產生了復雜的激波干擾流場，相比三線性和逆向距離權方法，用守恒插值方法計算得到的激波分布更為精細、光滑。

4.3 三維機翼分離投放模型

選擇機翼/掛架/帶舵外掛物(Wing/Pylon/Finned-Store，WPFS)模型，對本文所建立的重疊網格守恒插值方法進行驗證。該模型是美國進行分離投放CFD數值驗證時使用的一個機翼和導彈的簡化模型，有詳實可靠的風洞試驗數據，因此常被當做驗證重疊網格分離投放計算的標準算例。外掛物共有4片尾翼，呈X形分布。在該試驗中，還使用了彈射力，使外掛物在分離初期保持抬頭趨勢，避免其尾部和掛架碰撞，具體數據詳見文獻[34]。

計算狀態取和文獻[34]一致：來流馬赫數Ma=0.95，初始迎角α=0°，初始側滑角為0°，本文采用非定常雷諾平均Navier-Stokes方程、S-A湍流方程、6自由度(DOF)方程來模擬計算該模型的外掛物分離歷程。采用6套重疊子網格進行計算，分別為：用于模擬計算的包裹機翼和掛架的背景網格、包裹帶掛物的子網格以及包裹每一個舵的子網格，總網格量為553萬。WPFS模型子網格的重疊效果如圖15(a)所示，表面網格如圖15(b)所示。

圖16(a)是初始狀態在執行“挖洞”操作后得到的重疊網格計算單元的剖面圖，物理量通過相互重疊的網格部分進行插值傳遞。圖16(b)是時間t=0.3 s時各個子網格相互重疊示意圖，可以看到在計算過程中，子網格跟隨物體位置的變化而變化。圖17給出了t=0 s時刻與t=0.3 s時刻的實時壓力分布云圖，計算得出的流場結構清晰合理。

將計算得到的外掛物分離動態特性同試驗數據進行比較，圖18(a)和圖18(b)分別為外掛物的質心位移隨時間的變化量以及對應時刻的姿態角。可以看出，計算得到的軌跡同試驗數據吻合較好，證明本文建立的重疊網格守恒插值方法準確有效，魯棒性強，工程實用。

5 結 論

1) 針對二階線性分布的流場變量，采用局部超網格方法在重疊網格區域可實現精確守恒插值，對非線性分布的流場變量，本文插值方法守恒性更高。

2) 結合局部超網格與ADT搜索方法，重疊網格插值單元能夠快速搜索到多個貢獻單元，合理地擴大了貢獻單元模板，提高了插值精度和流場光滑性，加快了殘差收斂速度。

3) 本文重疊網格守恒插值方法適用于非結構網格與結構網格的各類型網格單元，工程實用、魯棒性強。插值時采用體積加權方法，當子網格尺度相差較大時，仍然能夠保持較好的流場光滑性與連續性。

本文發展了一種重疊網格守恒插值新方法，下一步將開展重疊網格洞面優化技術與嵌入網格方法，進一步提高重疊子網格尺度相差較大時流場的光滑性。

參 考 文 獻

[1] 李鵬, 高振勛, 蔣崇文. 重疊網格方法的研究進展[J]. 力學與實踐, 2014, 36(5):551-565.

LI P, GAO Z X, JIANG C W. The progress of the overlapping grid techniques[J]. Mechanics in Engineering, 2014, 36(5):551-565(in Chinese).

[2] SHIH T I P. Overset grids: Fundamentals and practical issues: AIAA-2002-3259[R]. Reston, VA: AIAA, 2002.

[3] 田書玲, 伍貽兆, 夏健. 用動態非結構重疊網格法模擬三維多體相對運動繞流[J]. 航空學報, 2007, 28(1):46-51.

TIAN S L, WU Y Z, XIA J. Simulation of flows past multi-body in relative motion with dynamic unstructured overset grid method[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(1): 46-51 (in Chinese).

[4] 伍貽兆, 田書玲, 夏健. 基于非結構動網格的非定常流數值模擬方法[J]. 航空學報, 2011, 32(1):15-26.

WU Y Z, TIAN S L, XIA J. Unstructured grid methods for unsteady flow simulation[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(1): 15-26 (in Chinese).

[5] MARSTIN C, MCCONNAUGHEY H. Computational problems on composite grids: AIAA-1984-1611[R]. Reston, VA: AIAA, 1984.

[6] KANG Z L, YAN C, YU J, et al. A fast and reliable overset unstructured grids approach[J]. Acta Mechanica Sinica, 2013, 29(2): 149-157.

[7] 黃宇, 閻超, 王文, 等. 混合重疊網格插值方法的改進及應用[J]. 北京航空航天大學學報, 2017, 43(2):285-292.

HUANG Y, YAN C, WANG W, et al. An improved interpolation method for hybrid overset grid and its application[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(2): 285-292 (in Chinese).

[8] 周乃春, 李彬, 鄭鳴, 等. 帶控制率導彈投放數值模擬[J]. 空氣動力學學報, 2013, 31(3): 107-115.

ZHOU N C, LI B, ZHENG M, et al. Missile separation simulation with control laws[J]. Acta Aerodynamica Sinica, 2013, 31(3): 107-115 (in Chinese).

[9] FARRELL P E, PIGGOTT M D, PAIN C C, et al. Conservative interpolation between unstructured meshes via supermesh construction[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198(33): 2632-2642.

[10] ZHENG Y, LIOU M S. Progress in the three-dimensional DRAGON grid scheme: AIAA-2001-2540[R]. Reston, VA: AIAA, 2001.

[11] XU K, SUN G, CAI J Y. On interface conservative attributions for computations of the complex flows of high-lift system based on chimera tech-nique[C]∥Computer and Automation Engineering (ICCAE), 2010 The 2nd International Conference on IEEE. Piscataway, NJ: IEEE Press, 2010: 279-283.

[12] 張宇飛, 陳海昕, 符松. 基于高階守恒重映對窗口嵌入技術的改進[J]. 計算物理, 2011, 28(2): 167-173.

ZHANG Y F, CHEN H X, FU S. Improvement on window embedment technology with high order conservative remapping[J]. Chinese Journal of Computational Physics, 2011, 28(2): 167-173(in Chinese).

[13] ZHAO X, GUAN H W, YANG Z, et al. An implicit and globally conservative unstructured chimera grid method: AIAA-2011-0777[R]. Reston, VA: AIAA, 2011.

[14] FARRELL P E, MADDISON J R. Conservative interpolation between volume meshes by local Galerkin projection[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(1): 89-100.

[15] MENON S, SCHMIDT D P. Conservative interpolation on unstructured polyhedral meshes: An extension of the supermesh approach to cell-centered finite-volume variables[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(41): 2797-2804.

[16] 徐春光, 董海波, 劉君. 基于單元相交的混合網格精確守恒插值方法[J]. 爆炸與沖擊, 2016, 36(3): 305-312.

XU C G, DONG H B, LIU J. An accurate conservative interpolation method for mixed grid based on the intersection of grid cells[J]. Explosion and Shock Waves, 2016, 36(3): 305-312 (in Chinese).

[17] 崔鵬程, 鄧有奇, 唐靜, 等．基于伴隨方程的網格自適應及誤差修正技術[J]．航空學報, 2016,37(10): 2992-3002.

CUI P C, DENG Y Q, TANG J, et al. Adjoint-based grid adaptation and error correction[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(10): 2992-3002 (in Chinese).

[18] BLAZEK J. Computational fluid dynamics: principles and applications[M]. 3rd ed. Oxford: Elsevier, 2015:75-120.

[19] KIM J S, KWON O J. Improvement on block LU-SGS scheme for unstructured mesh Navier-Stokes computations: AIAA-2002-1061[R]. Reston, VA: AIAA, 2002.

[20] SPALART S R. A one-equation turbulence model for aerodynamic flows: AIAA-1992-0439[R]. Reston, VA: AIAA, 1992.

[21] ROE P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372.

[22] 李彬, 唐靜, 鄧有奇, 等. 并行的多重網格方法在離散伴隨優化中的應用[J]. 航空學報, 2014, 35(8): 2091-2101.

LI B, TANG J, DENG Y Q, et al. Application of parallel multigrid algorithm to discrete adjoint optimization[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(8): 2091-2101 (in Chinese).

[23] BEATRICE R, JAY S. Robust and scalable overset grid assembly for partitioned unstructured meshes: AIAA-2013-0797[R]. Reston, VA: AIAA, 2013.

[24] THEOHARIS T, IAN P. Two parallel methods for polygon clipping[J]. Computer Graphics Forum, 2010, 8(2):107-114.

[25] MARTINEZ F, RUEDA A J, FEITO F R. A new algorithm for computing Boolean operations on polygons[J]. Computers & Geosciences, 2009, 35(6): 1177-1185.

[26] 唐靜, 鄧有奇, 馬明生, 等. 飛翼氣動優化中參數化和網格變形技術研究[J]. 航空學報, 2015, 36(5): 1480-1490.

TANG J, DENG Y Q, MA M S, et al. Parametrization and grid deformation techniques for fly-wing shape optimization[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1480-1490 (in Chinese).

[27] ALAUZET F, MEHRENBERGER M. P1-conservative solution interpolation on unstructured triangular meshes[J]. International Journal for Numerical Methods in Engineering, 2010, 84(13): 1552-1588.

[28] GARIMELLA R, KUCHARIK M, SHASHKOV M. An efficient linearity and bound preserving conservative interpolation (remapping) on polyhedral meshes[J]. Computers & Fluids, 2007, 36(2): 224-237.

[29] MAYEUR J, DUMONT A, DESTARAC D, et al. RANS simulations on TMR test cases and M6 wing with the ONERA elsA flow solver: AIAA-2015-1745[R]. Reston, VA: AIAA, 2015.

[30] DURRANI N, QIN N. Comparison of RANS, DES and DDES results for ONERA M6 wing at transonic flow speed using an in-house parallel code: AIAA-2011-0190[R]. Reston, VA: AIAA, 2011.

[31] DA SILVA R G, AZEVEDO J L F, BASSO E. Simulation of ONERA M6 wing flows for assessment of turbulence modeling capabilities: AIAA-2016-0549[R]. Reston, VA: AIAA, 2016.

[32] SAXENA S K, NAIR M T. Implementation and testing of Spalart-Allmaras model in a multi-block code: AIAA-2002-0835[R]. Reston, VA: AIAA, 2002.

[33] LUO H, BAUM J D, L?HNER R. A Hermite WENO-based limiter for discontinuous Galerkin method on unstructured grids[J]. Journal of Computational Physics, 2007, 225(1): 686-713.

[34] HEIM E R. CFD wing/pylon/finned store mutual interference wind tunnel experiment: AEDC-TSR-91-P4[R]. New York: AEDC, 1991.