局部催化特性差異對氣動熱環境影響的計算分析

丁明松,董維中，高鐵鎖，江濤，劉慶宗

中國空氣動力研究與發展中心 計算空氣動力研究所，綿陽 621000

高超聲速飛行器在再入和滑翔過程中，如果飛行速度很高(一般認為馬赫數為10以上)，會出現高溫氣體效應[1-2](或真實氣體效應)。高溫氣體效應包括熱化學平衡、非平衡和凍結3種狀態[3-4]，可以統一采用高溫氣體非平衡效應進行描述(將凍結和平衡流可以看作非平衡流動的兩種極限狀態)。高溫氣體非平衡效應對飛行器氣動特性造成顯著影響[5-7]，一方面氣體分子能量激發和化學反應會吸收大量的能量，使流場的溫度降低;另一方面高溫下的非完全氣體性質使得流場中激波位置和分離區大小等流動性狀發生改變，從而改變了整個飛行器的氣動熱環境。

在高溫氣體非平衡流動氣動熱環境數值模擬過程中，很關鍵的一個技術問題是壁面催化效應的模擬。高溫氣體流場中原子和離子在到達壁面時會發生表面催化復合反應，釋放出很大的結合能，不僅影響非平衡流動，而且產生較大組分擴散熱流，對飛行器氣動熱環境造成顯著影響[8]。

在數值模擬中，催化效應常以邊界條件的形式給出，確定飛行器表面的氣體組分分布。完全非催化(Non-Catalytic Wall, NCW)和完全催化(Fully Catalytic Wall, FCW)是高超聲速飛行器氣動熱環境數值模擬中最容易實現的兩種催化邊界條件。完全非催化是假設壁面材料的催化速率為零，此時壁面處組分分布不存在法向梯度，與流場法向內點組分分布相等。完全催化則認為壁面材料的催化能力非常強，催化速率接近于無窮大，流場中高能原子和離子在壁面處將完全復合，釋放出最大限度的結合能。可見，完全非催化和完全催化是壁面催化的兩種極限情況，精確地模擬催化效應須考慮壁面材料實際的催化特性，還可能用到有限催化條件(Partially Catalytic Wall, PCW)邊界計算模型。它一般通過求解壁面附近質量守恒方程的方法構建，不考慮質量引射時，氣體組分由催化反應生成(或消耗)的質量與擴散出(或入)壁面微元的質量相等。其中，催化復合反應速率常數計算是有限催化模型的關鍵。根據催化復合反應速率常數計算方法的不同，有限催化模型主要分為兩類：一類是給定催化系數，進而得到催化復合反應速率常數[9-10]；另一類是對氣固催化復合反應過程進行分析和建模，運用表面有限速率化學反應動力學方法，得到催化反應速率常數[11]。第一類方法相對簡單，有大量防熱材料催化系數試驗數據支持[12]，因此應用相對廣泛[13-14]。

由于高超聲速飛行過程中飛行器表面各部位受熱、受力情況存在很大差別，因此，在飛行器設計過程中，飛行器表面常采用多種材料結構。在這些情況下，飛行器表面不同位置催化特性將存在差別，可能對氣動熱環境造成較大影響，要實現高超聲速飛行器氣動熱環境精確預測，必須考慮多種壁面材料特性條件下的壁面催化效應。

國外很早就開始了高溫氣體效應以及壁面催化效應的研究，研究水平相對成熟。表面材料催化特性研究多結合試驗進行。例如，Inger[15]發現壁面催化能力不僅受材料物理化學特性影響，而且受壁面溫度影響，在此基礎上，提出了某碳基材料催化復合系數隨表面溫度變化的擬合公式。Goulard[16]通過試驗開展了典型材料壁面催化復合系數研究，大致給出了典型氧化物和金屬材料對氧原子復合反應的催化復合系數。Kurotaki[9-10]、Stewart[17]、Scott[18]等通過試驗測量、理論分析和數值模擬等方法，建立了可用于數值模擬的壁面催化模型，開展了典型材料(碳基、硅基熱防護材料等)的壁面催化復合系數研究，并給出了在較低溫條件下(小于2 000 K)大多數碳基和硅基熱防護材料壁面催化復合系數小于0.1的結論。這些研究表明，壁面附近氣體的非平衡特性、壁面溫度以及壁面材料催化復合系數是影響壁面催化效應的主要因素。

在高溫非平衡流動催化效應數值應用研究方面，國外還形成了一些較為成熟的流場軟件。例如，Subrahmanyam[19]開展了高溫氣體的物理化學模型、表面催化計算模型、輻射平衡表面溫度分布計算模型以及材料催化復合特性研究，給出了計算軟件SPARTA在氣動熱環境分析方面的發展和應用情況。Edquist[20]采用LAURA計算軟件，考慮有限催化特性和表面輻射平衡溫度，開展了火星探測器MSL氣動熱環境研究。

國內在高溫氣體非平衡效應以及催化效應方面的研究時間較長，已有顯著進步。例如，2000年，董維中等[21]開展了駐點壁面催化速率常數確定的研究，依據激波管試驗測量確定了Pt、SiO2等材料的表面催化速率，給出了駐點熱流隨催化速率常數變化的規律。2001年，曾明等[22]研究了不同熱化學模型及壁面催化條件對表面傳熱的影響,分析比較了不同組元的高溫空氣模型、不同熱力模型和不同壁面催化條件。2004年，柳軍[23]開展熱化學非平衡流動的試驗和數值模擬研究，建立了TCNEQ(2D、3D)計算程序，開展了Apollo飛船返回艙大迎角全流場的數值模擬。高冰等[24]開展了高溫真實氣體效應中催化效應對氣動熱影響的試驗探索，發現催化效應隨著迎角的增大表現更明顯，經分析認為是由于迎角增大非平衡效應變強造成的。2014年，金華[25]開展了防熱材料表面催化特性測試與評價方法研究，獲得了環境參數(壓力、溫度、氧原子濃度)與材料屬性(成分、表面粗糙度)對ZrB2、SiC以及ZrB2-SiC材料催化特性的影響規律。2011—2014 年，苗文博等[26-28]開展不同飛行條件下催化特性對氣動特性(包括氣動熱環境和氣動力特性)的影響研究，取得了一系列有價值的結論。2017年，楊肖峰和唐偉[29]開展了火星進入器考慮多種催化作用的高超聲速非平衡氣動加熱數值模擬研究，發現壁面催化效應對化學非平衡氣動加熱影響顯著，完全催化壁預測值最為保守，而完全非催化壁結果最低,差別高達數倍。

盡管國內在高溫非平衡效應及表面催化效應數值模擬、理論分析和試驗測量等方面取得了非常大的發展，但仍與國外水平存在一定差距：由于壁面催化效應受流場中的高溫非平衡效應、壁面溫度以及壁面材料催化復合系數等多個因素綜合影響，而壁面材料催化復合系數又受材料成分、材料結構、表面溫度以及表面粗糙度、氧化程度等因素影響，因此很難確定實際飛行過程中飛行器壁面催化效應的強弱。為此，在飛行器氣動熱防護設計過程中，常作完全催化壁面或完全非催化壁面假設，即在氣動熱環境數值模擬預測過程中，認為飛行器表面催化特性為全機表面完全催化或完全非催化，并以這兩者結果作為上下限，實際飛行過程中飛行器的各部位表面熱流均應處于這兩者結果之間。這種簡化處理不僅較大程度地影響了氣動熱環境預測的精度，可能造成飛行器熱管理的“過防護”，而且其可靠性也缺乏驗證。目前國內尚未見到有關飛行器表面不同位置催化特性差異性對氣動熱環境影響的研究，其作用大小和影響規律尚不明確。在這種情況下，是否可作壁面催化效應的簡化處理，還需要進一步開展研究。

作者所在研究團隊對高超聲速飛行器非平衡效應及其壁面催化效應和飛行器氣動熱環境進行了較為廣泛的研究[5-8,21,30-31]。本文在以往工作的基礎上，通過求解熱化學非平衡Navier-Stokes方程，完善有限催化條件下高溫熱化學非平衡流場氣動熱環境數值計算方法和計算程序，并加以驗證。在此基礎上，針對飛行器表面局部催化特性差異，開展不同條件下高溫熱化學非平衡流場氣動熱環境數值模擬，分析局部催化特性差異對飛行器氣動熱環境的影響。

1 數值計算方法

控制方程是三維熱化學非平衡Navier-Stokes方程，無量綱化形式為[5]

(1)

式中：Q為守恒變量；Re為雷諾數；F、G、H和Fv、Gv、Hv分別對應x、y、z方向的對流項與黏性項；W為非平衡源項。對流項采用AUSMPW+(Advection Upstream Splitting Method by Pressure-based Weight functions)格式離散，黏性項采用中心格式離散，隱式時間離散采用LU-SGS(Lower-Upper Symmetric Gauss Seidel)方法。為了克服方程的非平衡剛性問題，對非平衡源項和對流項采用全隱式處理。具體計算公式和方法見文獻[5]。

2 物理化學模型

2.1 熱化學反應模型

空氣模型可選用5組分(N2、O2、NO、N、O)或7組分(N2、O2、NO、N、O、NO+、e)模型；化學反應模型可選用Dunn-Kang模型[5]或Park模型[32];熱力學模型可采用一溫度模型和兩溫度模型，在兩溫度模型中考慮振動非平衡效應。具體計算公式和方法見文獻[5，30-31]。

2.2 表面催化模型和表面溫度計算方法

NCW和FCW處理方法詳見文獻[5]。對于PCW，主要考慮氮原子和氧原子的復合反應以及離子和電子的復合反應[33]，具體為

式中：r為反應編號，上述反應可以認為是不可逆的。反應速率常數的表達式為

(2)

式中：R0為普適氣體常數；αr∈[0,1]為壁面催化復合系數，來源于材料的試驗數據;Tw為壁面溫度；M1、M2和M3分別為O、N、NO的摩爾質量。由上述反應引起的組分質量生成率分別為

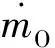
表面溫度條件通常采用等溫壁條件，但在實際情況中，由于飛行器不同部位的氣動加熱差別較大，飛行器不同表面溫度存在差異。這里考慮表面輻射效應、催化效應和振動非平衡效應，輻射平衡的表面溫度(壁面輻射平衡溫度)由以下能量守恒方程確定[19-20]：

(3)

式中：Q為飛行器表面熱流(一般由平轉動溫度熱流、振動溫度熱流和組分擴散熱流組成)；ε為表面材料輻射系數；σ為斯忒藩-玻耳茲曼常數。

3 計算方法驗證

3.1 非平衡流場表面熱流數值計算

所采用的測量熱流的飛行試驗模型為鈍錐標模ELECTRE[34]，其總長度為2 m，頭部半徑為0.175 m，半錐角為4.6 °，結構示意圖見圖1。飛行試驗條件為：來流速度為4 230 m/s，來流密度為6.995×10-4kg/m3，來流溫度為265 K，壁面溫度為343 K。采用7組分空氣模型和兩溫度熱力學非平衡模型，化學反應模型采用Dunn-Kang模型(與文獻[34]保持一致)，考慮NCW和FCW壁面條件，主要考核熱流分布計算結果。圖2給出了沿軸線方向(X方向)表面熱流分布，并與文獻[34]、飛行試驗數據進行了比較。可以看出：本文的計算結果與文獻[34]的計算結果幾乎完全重合，與飛行試驗結果也符合較好，這說明本文非平衡流場表面熱流數值計算結果具有較高的可信度。

3.2 非平衡流場壁面有限催化數值計算

采用球頭模型[33]開展非平衡流場壁面有限催化數值考核驗證,球頭半徑為5.08 cm。計算狀態為：來流溫度為970.0 K，來流振動溫度為2 800.0 K，來流壓力為96.12 Pa，來流速度為5 630.0 m/s，壁面溫度為1 000 K。高溫空氣組分模型采用5組分空氣模型(與文獻[33]一致)；化學反應模型采用Dunn-Kang模型或Park模型；熱力學模型采用兩溫度模型；表面材料催化條件為NCW、FCW或PCW。考慮有限催化PCW時，催化復合系數為0.000 1～1.0。

圖3給出了非催化條件下流場中氮氣質量分數(cN2)和振動溫度(Tv)的分布。可以看出，流場中化學反應十分劇烈，振動溫度最高被激發至8 000 K以上。圖4給出了表面熱流與文獻[33]的比較，圖中S為表面弧長，R為球頭半徑，QFCW為完全催化條件下的駐點熱流。可以看出，不同催化條件下的本文計算熱流及其分布變化規律與文獻[33]基本完全一致，這說明本文非平衡流場壁面有限催化數值計算結果具有較高可信度。

4 催化特性差異對氣動熱的影響

為了保證計算可靠性，這里采用3.1節給出的ELECTRE外形、計算來流條件和壁溫條件，計算采用的物理化學模型也與3.1節完全相同。為了分析不同部位催化特性差異對氣動熱環境的影響，飛行器表面設置了兩種不同催化特性的材料(分別標識為M1和M2)，飛行器表面大部分區域采用M1材料，局部小范圍表面(沿氣流流向表面長度約15 mm的區域)采用M2材料。按照表面M2材料分布的不同分為6種方案，如表1所示，表中以鈍錐體軸線為X軸，以鈍錐體球頭與X軸的交點為坐標原點。

首先開展M1為完全非催化壁面材料(如陶瓷等材料[8]，催化能力弱)、M2為完全催化材料(如金屬Cu、Pt等材料[8,25]，催化能力較強)的數值計算分析。

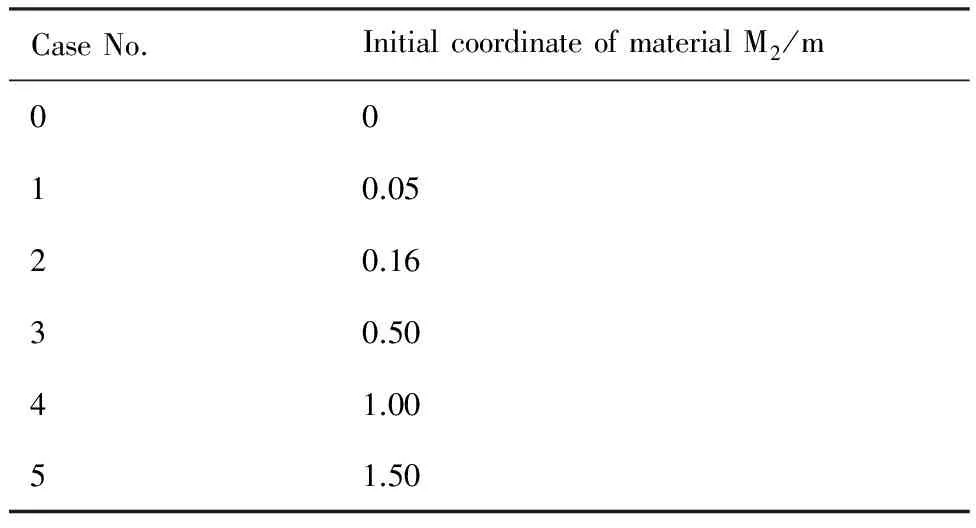
表1 M2材料的6種分布方案Table 1 Six distribution cases of material M2

圖5給出了Case 2鈍錐表面熱流云圖。可以定性地看出，表面催化特性變化會造成局部熱流跳變，完全催化區域(M2材料)熱流遠高于其周圍完全非催化區域(M1材料)，這與一般認知是相符的,即強烈的壁面催化效應會使表面熱流顯著升高。

為了進一步定量地分析其影響程度，圖6給出不同方案表面熱流沿軸向的分布以及其最值和平均值分布，圖6中曲線標號Case 0～Case 5分布對應表1中6 個不同方案的熱流結果，FCW和NCW分別對應鈍錐體全表面FCW和NCW的結果，圖6(b)中Qmax和Qaverage分別為熱流最大值和平均值。由圖6可以看出，除Case 0外，催化特性變化對表面熱流影響極大，其最大值和平均值均遠高于飛行器全表面FCW模擬的同一區域結果，其差別甚至可達到一個量級以上，這種情況不僅發生在熱化學反應強烈的頭部，而且在熱化學反應相對較弱的身部區域也是如此。這說明，在某些情況下，將飛行器在全表面FCW和NCW條件下的數值模擬結果作為實際飛行過程中表面熱流上、下限的這一簡化處理方式，是不可取的。

為了分析這一現象產生的原因，圖7給出了高能粒子氧原子質量分數分布云圖。圖7(a)為Case 2的氧原子質量分布云圖，圖7(b)為圖7(a)中圓圈區域放大圖，圖7(c)為飛行器全表面FCW數值模擬時圖7(b)對應區域的云圖。

圖8(a)和圖8(b)分別為Case 2和Case 0的表面熱流沿軸向分布局部放大圖，以及與全FCW和全NCW時的熱流分布比較。由圖7(b)和圖7(c)可以看出，對于Case 2，由于鈍錐頭部為NCW壁面條件，高能粒子(如O等)在壁面處復合程度較低，因此表面附近其濃度遠遠高于全區域FCW的情況；當高濃度的高能粒子流經表面材料M2(FCW)所在區域，就會發生大量復合反應，釋放出化學能，使壁面熱流顯著提升。由圖8(a)可見，對于Case 2，在表面材料M2(FCW)所在區域存在兩個峰值，峰值1遠高于峰值2。這是符合理論分析的：峰值1產生的主要原因應該是氣流沿流向流動和擴散作用共同帶來的高濃度高能粒子(如O、N等)在材料交界面附近大量復合，使其熱流急劇上升，形成熱流峰值，而峰值2產生的主要原因僅僅是高能粒子從高濃度區域向低濃度區域反流向的擴散作用。而對于Case 0，表面材料M2(FCW)所在區域只存在一個峰值(見圖8(b))，這一區域不存在由氣流沿流向流動帶來的高能粒子，因而材料催化差異性影響相對較小。

接下來再來看反過來的情況：大面積區域M1為完全催化壁面材料、局部M2為完全非催化材料。圖9給出了這一情況下，不同方案的軸向熱流比較，圖中標識與圖6(a)和圖8(a)類似。由圖可以看出，當大面積為FCW，較小局部為NCW時，在不同材料的交界面也會出現熱流的急劇上升區域，形成峰值熱流，其大小明顯高于全機FCW的結果。不同的是，圖9(b)中峰值1小于峰值2，其產生原因恰好與圖8(a)反過來：峰值1產生的主要原因僅僅是高能粒子從高濃度區域向低濃度區域反流向的擴散作用，而峰值2產生的主要原因是氣流沿流向流動和擴散作用共同帶來的高濃度高能粒子(如O、N等)在材料交界面附近大量復合，使其熱流急劇上升，形成熱流峰值。

NCW和FCW是壁面催化效應的兩種極限狀態，在飛行器真實的飛行過程中，飛行器表面催化效應很可能處于有限催化(PCW)狀態。為此，圖10給出了全表面不同催化復合系數條件下數值模擬得到的駐點熱流及催化復合系數對熱流影響的效率D(簡稱影響效率)，其表達式為

(4)

式中：Q0為當前αr條件數值計算得到的駐點熱流；QFCW和QNCW分別為全表面FCW和全表面NCW數值模擬得到的駐點熱流。

由圖10可以看出，表面催化復合系數對熱流的影響并不是線性關系，其影響效率變化較大的區域為0.001～0.1，分別對應影響效率為9.04%～92.83%。而這一區間恰好是現有的大多數硅基、碳基熱防護材料催化復合系數所處范圍[11-14]。

為了分析有限催化條件下，表面材料催化特性差異性對熱環境的影響，針對Case 1開展氣動熱環境數值模擬。表面大部分區域M1材料的催化復合系數αM1設為0.001、0.01或0.1，局部區域M2材料的催化復合系數αM2設為0.05或0.1。表面溫度條件為等溫壁面條件Tw=343 K或輻射平衡(Radiative Equilibrium，RE)的壁溫條件。圖11給出了Case 1的局部催化特性變化區域表面熱流和表面溫度沿軸向分布。可以看出：有限催化條件下，壁面催化復合系數的差異性同樣會帶來局部熱流的跳變，使局部區域熱流明顯高于全表面催化復合系數為0.1的情況；壁面復合系數差異越大，熱流跳變的程度越大；熱流的跳變還會帶來壁面輻射平衡溫度的跳變，當αM1=0.001、αM2=0.1時，表面溫度跳變可達300 K以上。

5 結 論

1) 本文考慮高溫空氣化學反應、氣體分子熱力學激發、流動中的非平衡效應和壁面催化效應，通過數值求解三維熱化學非平衡Navier-Stokes方程和壁面處質量與能量平衡關系，完善了高溫熱化學非平衡流場有限催化氣動熱環境數值計算方法和計算程序。

2) 考核驗算表明：飛行器高溫氣體熱化學非平衡流場氣動熱環境數值模擬結果與文獻結果、飛行試驗結果符合，表面熱流數值計算結果具有較高的可信度；非平衡流場壁面有限催化數值計算結果與文獻符合，本文有限催化數值模擬具有較高可信度。

3) 針對ELECTRE外形，開展了不同條件下高溫氣體熱化學非平衡氣動熱環境模擬，分析了局部催化特性差異對氣動熱環境的影響。在本文的計算條件下，局部催化特性差異會對氣動熱環境造成不可忽視的影響：不同催化特性表面材料接口處會出現熱流跳變，其機理與流場中高能粒子沿流向的流動和擴散作用有關；熱流跳變量受催化特性差異量、材料分布方式影響；催化特性差異較大時，局部區域熱流可能遠遠高于飛行器全表面完全催化的熱流結果，其差別甚至可達1個量級以上；在某些情況下，將飛行器全表面FCW和NCW條件下的數值模擬結果作為實際飛行過程中表面熱流上、下限的這一簡化處理方式，是不可取的；熱流的跳變還會帶來壁面溫度的跳變，某些條件下表面輻射平衡溫度跳變可達300 K以上。

由此可見，在飛行器氣動熱數值模擬預測過程中，應盡可能考慮表面材料真實的有限催化特性，以減小由于催化效應帶來的不確定度。同時，在飛行器氣動熱防護設計過程中，應盡量保證飛行器表面各部位的催化特性一致或者差異較小，以減少由于局部催化特性差異帶來的影響。盡管本文對局部催化特性進行了一定程度的分析，但這方面的工作還尚未徹底完成，后續將結合具體的工程應用，開展更深入細致的分析研究。

參 考 文 獻

[1] BOYD I D. Modeling of associative ionization reactions in hypersonic rarefied flows[J]. Physics of Fluids, 2007, 19(9): 3-14.

[2] OZAWA T, LEVIN D A, NOMPELIS I, et al. Particle and continuum method comparison of a high altitude Mach number reentry flow[J]. Journal of Thermophysics and Heat Transfer, 2010, 24(2): 225-240.

[3] LOFTHOUSE A J, SCALABRINY L C, BOYD I D. Hypersonic aerothermodynamics analysis across non-equilibrium regimes using continuum and particle methods: AIAA-2007-3903[R]. Reston, VA: AIAA, 2007.

[4] WEN C Y, MASSIMI H S, CHEN Y S, et al. Numerical simulations of non-equilibrium flows over rounded models at reentry speeds: AIAA-2012-5906[R]. Reston, VA: AIAA, 2012.

[5] 董維中. 熱化學非平衡效應對高超聲速流動影響的數值計算與分析[D]. 北京: 北京航空航天大學, 1996: 3-30.

DONG W Z. Numerical simulation and analysis of thermo-chemical non-equilibrium effects at hypersonic flows[D]. Beijing: Beihang University, 1996: 3-30 (in Chinese).

[6] 董維中. 氣體模型對高超聲速再入鈍體氣動參數計算影響的研究[J]. 空氣動力學學報, 2001, 19(2): 197-202.

DONG W Z. Thermal and chemical model effect on the calculation of aerodynamic parameter for hypersonic reentry blunt body[J]. Acta Aerodynamica Sinica, 2001, 19(2): 197-202 (in Chinese).

[7] 董維中, 高鐵鎖, 丁明松, 等. 高超聲速非平衡流場多個振動溫度模型的數值研究[J]. 空氣動力學學報, 2007, 25(1): 1-6.

DONG W Z, GAO T S, DING M S, et al. Numerical studies of the multiple vibrational temperature model in hypersonic non-equilibrium flows[J]. Acta Aerodynamica Sinica, 2007, 25(1): 1-6 (in Chinese).

[8] 樂嘉陵. 再入物理[M]. 北京: 國防工業出版社, 2005: 9-21.

LE J L. Reentry physics[M]. Beijing: National Defence Industry Press, 2005: 9-21 (in Chinese).

[9] KUROTAKI T. Construction of catalytic model on SiO2-based surface and application to real trajectory: AIAA-2000-2366[R]. Reston, VA: AIAA, 2000.

[10] KUROTAKI T, MATSUZAKI T. CFD evaluation of catalytic model on SiO2-based TPS in arc-heated wind tunnel: AIAA-2003-0155[R]. Reston, VA: AIAA, 2003.

[11] JOCHEN M, MATTHEW M. Finite-rate surface chemistry model, I: Formulation and reaction system examples: AIAA-2011-3783[R]. Reston, VA: AIAA, 2011.

[12] STEWART D A. Surface catalysis and characterization of proposed candidate TPS for access-to-space vehicles: NASA TM-112206 [R]. Washington, D.C.: NASA, 1997.

[13] STEWART D A. Effect of non-equilibrium flow chemistry and surface catalysis on surface heating to AFE: AIAA-1991-1373[R]. Reston, VA: AIAA, 1991.

[14] ANTONIO V. Effect of finite rate chemical models on the aerothermodynamics of reentry capsules: AIAA-2008-2668[R]. Reston, VA: AIAA, 2008.

[15] INGER G R. Nonequilibrium hypersonic stagnation flow at low Reynolds numbers: TDR-269(4230-20)-10[R]. EI Segundo, CA: Aerospace Corporation, 1964.

[16] GOULARD R J. On catalytic recombination rates in hypersonic stagnation on heat transfer[J]. Jet Propulsion, 1958, 28(11): 737-745．

[17] STEWART D A, RAKICH J V, LANFRANCO M J. Catalytic surface experiment on the space shuttle: AIAA-1981-1143[R]. Reston, VA: AIAA, 1981.

[18] SCOTT C D. Wall catalytic recombination and boundary conditions in non-equilibrium hypersonic flows—With applications: 94A10765[R]. Washington, D.C.: NASA, 1992．

[19] SUBRAHMANYAM P. Development of a parallel CFD solver SPARTA for aerothermodynamic analysis: AIAA-2007-2976[R]. Reston, VA: AIAA, 2007.

[20] EDQUIST K T. Afterbody heating predictions for a Mars science laboratory entry vehicle: AIAA-2005-4817[R]. Reston, VA: AIAA, 2005.

[21] 董維中, 樂嘉陵, 劉偉雄. 駐點壁面催化速率常數確定的研究[J]. 流體力學實驗與測量, 2000, 14(3): 1-6.

DONG W Z, LE J L, LIU W X. The determination of catalytic rate constant of surface materials of testing model in the shock tube[J]. Experiments and Measurements in Fluid Mechanics, 2000, 14(3): 1-6 (in Chinese).

[22] 曾明, 馮海濤, 瞿章華. 不同熱化學模型對表面傳熱影響的數值分析[J]. 國防科技大學學報, 2001, 23(5): 27-31.

ZENG M, FENG H T, QU Z H. Numerical analysis of the effects for different thermo-chemical models on heat transfer[J]. Journal of National University of Defense Technology, 2001, 23(5): 27-31 (in Chinese).

[23] 柳軍. 熱化學非平衡流及其輻射現象的實驗和數值計算研究[D]. 長沙: 國防科學技術大學, 2004: 3-25.

LIU J. Experimental and numerical research on thermo-chemical nonequilibrium flow with radiation phenomenon[D]. Changsha: National University of Defense Technology, 2004: 3-25 (in Chinese).

[24] 高冰, 杭建, 林貞彬, 等. 高溫真實氣體效應中催化效應對氣動熱影響的實驗探索[J]. 流體力學實驗與測量, 2004, 18(2): 55-58.

GAO B, HANG J, LIN Z B, et al. The experiment exploration of catalyst effects on aerodynamic heat in real gas effects[J]. Experiments and Measurements in Fluid Mechanics, 2004, 18(2): 55-58 (in Chinese).

[25] 金華. 防熱材料表面催化特性測試與評價方法研究[D]. 哈爾濱: 哈爾濱工業大學, 2014: 2-50.

JIN H. Surface catalyticity properties testing and characterization methods of thermal protection materilas[D]. Harbin: Harbin Institute of Technology, 2014: 2-50 (in Chinese).

[26] 苗文博, 程曉麗, 艾邦成. 來流條件對熱流組分擴散項影響效應分析[J]. 空氣動力學學報, 2011, 29(4): 476-480.

MIAO W B, CHENG X L, AI B C. Flow configuration effects on mass diffusion part of heat-flux in thermal-chemical flows[J]. Acta Aerodynamica Sinica, 2011, 29(4): 476-480 (in Chinese).

[27] 苗文博, 程曉麗, 艾邦成. 高超聲速流動壁面催化復合氣動加熱特性[J]. 宇航學報, 2013, 34(3): 442-446.

MIAO W B, CHENG X L, AI B C. Surface catalysis recombination aero-heating characteristics of hypersonic flow[J]. Journal of Astronautics, 2013, 34(3): 442-446 (in Chinese).

[28] 苗文博, 羅曉光, 程曉麗, 等. 壁面催化對高超聲速飛行器氣動特性影響[J]. 空氣動力學學報, 2014, 32(2): 236-239.

MIAO W B, LUO X G, CHENG X L, et al. Surface recombination effects on aerodynamic loads of hypersonic vehicles[J]. Acta Aerodynamica Sinica, 2014, 32(2): 236-239(in Chinese).

[29] 楊肖峰, 唐偉. 火星環境高超聲速催化加熱特性[J]. 宇航學報, 2017, 38(2): 205-211.

YANG X F, TANG W. Hypersonic catalytic aeroheating characteristics for mars entry process[J]. Journal of Astronautics, 2017, 38(2): 205-211 (in Chinese).

[30] 董維中, 丁明松, 高鐵鎖, 等. 熱化學非平衡模型和表面溫度對氣動熱計算影響分析[J]. 空氣動力學學報, 2013, 31(6): 692-698.

DONG W Z, DING M S, GAO T S, et al. The influence of thermo-chemical non-equilibrium model and surface temperature on heat transfer rate[J]. Acta Aerodynamica Sinica, 2013, 31(6): 692-698 (in Chinese).

[31] 董維中, 高鐵鎖, 丁明松, 等. 高超聲速飛行器表面溫度分布與氣動熱耦合數值研究[J]. 航空學報， 2015， 36(1): 311-324.

DONG W Z, GAO T S, DING M S, et al. Numerical study of coupled surface temperature distribution and aerodynamic heat for hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 311-324 (in Chinese).

[32] PARK C. Review of chemical-kinetic problems of future NASA missions, I: Earth entries[J]. Journal of Thermophysics and Heat Transfer, 1993, 7(3): 385-398.

[33] GOKCEN T. Effects of flow field non-equilibrium on convective heat transfer to a blunt body: AIAA-1996-0325[R]. Reston, VA: AIAA, 1996.

[34] MUYLAERT J. Standard model testing in the European high facility F4 and extrapolation to flight: AIAA-1992-3905[R]. Reston, VA: AIAA, 1992.