聚焦導數壓軸試題 破譯高考命題密碼

■廣東省興寧市第一中學　藍云波

導數是高中數學的重要內容,在高考中通常占據壓軸題的位置,其重要性不言而喻。通過對近幾年全國卷導數壓軸題的分析,可發現函數與導數壓軸題綜合性強,方法多樣,技巧性強,難度頗大。這類試題題型多樣,常考常新,但解題的關鍵在于數學思想方法的合理使用。為幫助同學們突破此類問題,下面從四個視角研究導數壓軸題的破解策略,以提高同學們的解題能力。

一、函數的單調性、最值

(河北省衡水中學2017屆高三上學期期中考試理科)已知函數f(x)=alnx+x2(a為實常數)。

(1)若a=-2,求證:函數f(x)在(1,+∞)上是增函數;

(2)求函數f(x)在[1,e]上的最小值及相應的x值;

(3)若存在x∈[1,e],使得f(x)≤(a+2)x成立,求實數a的取值范圍。

若a≥-2,則f'(x)在[1,e]上非負(僅當a=-2,x=1時,f'(x)=0),故函數f(x)在[1,e]上是增函數,此時f(x)min=f(1)=1。

f(x)min=

若a≤-2e2,f'(x)在[1,e]上非正(僅當a=-2e2,x=e時,f'(x)=0),故函數f(x)在[1,e]上是減函數,此時f(x)min=f(e)=a+e2。

綜上可知,當a≥-2時,f(x)的最小值為1,相應的x值為1;

當a≤-2e2時,f(x)的最小值為a+e2,相應的x值為e。

(3)不等式f(x)≤(a+2)x,可化為a(x-lnx)≥x2-2x。

因為x∈[1,e],所以lnx≤1≤x且等號不能同時取,即lnx＜x,故x-lnx＞0。

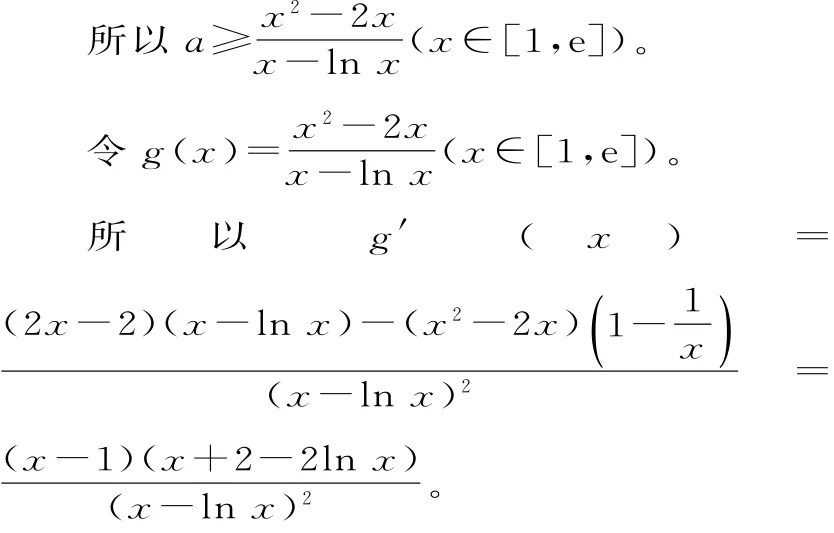
當x∈[1,e]時,x-1≥0,lnx≤1,故x+2-2lnx＞0,從而g'(x)≥0(僅當x=1時取等號),所以g(x)在[1,e]上為增函數。

故g(x)的最小值為g(1)=-1,所以a的取值范圍是[-1,+∞)。

點評:求解含參數的函數最值問題,關鍵是對參數進行分類討論。對于第三問的能成立問題,則是通過分離參數,轉化為新的函數的最小值求解。在解題中,特別要注意恒成立問題與能成立問題的區別。

(湖南省岳陽市2017屆高三聯考理科改編)已知函數f(x)=ln(x+1)-

(1)當a=1時,求函數f(x)在x=e-1處的切線方程;

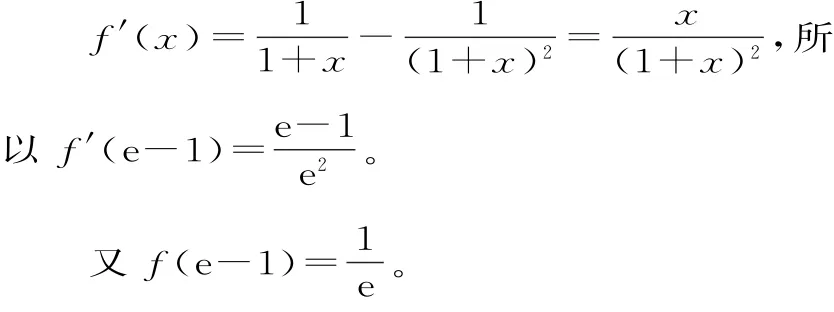
所以當a=1時,函數f(x)在x=e-1處的切線的斜率為

此時f(x)在(-1,0),(2a-3,+∞)上單調遞增,在(0,2a-3)上單調遞減。

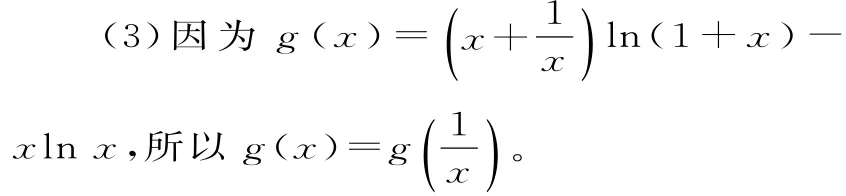
因此g(x)在(0,+∞)上的最大值等于其在(0,1]上的最大值。

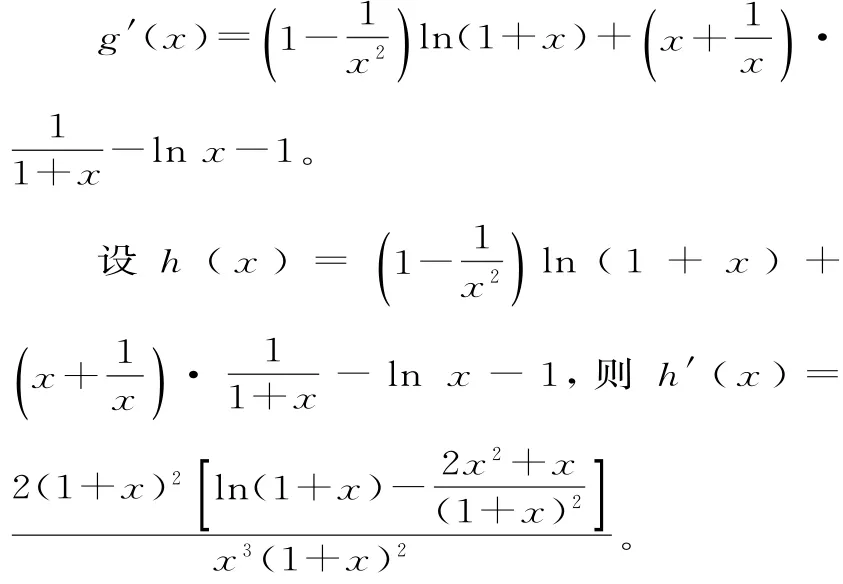
由(2)知,當a=2時,f(x)在區間(0,1]上單調遞減,所以f(x)=ln(1+x)-h(x)在區間(0,1]上單調遞減,于是h(x)≥h(1)=0。

從而函數g(x)在區間(0,1]上單調遞增,進而g(x)≤g(1)=2ln2,即g(x)的最大值為ln4。

點評:本題通過對函數g(x)的細致觀察,發現g(x)=g(),從而把研究問題的范圍縮小,實現了化難為易的效果。在求最值的過程中,還使用了二次求導的技巧。

二、函數的零點問題

(1)討論函數f(x)的單調性;

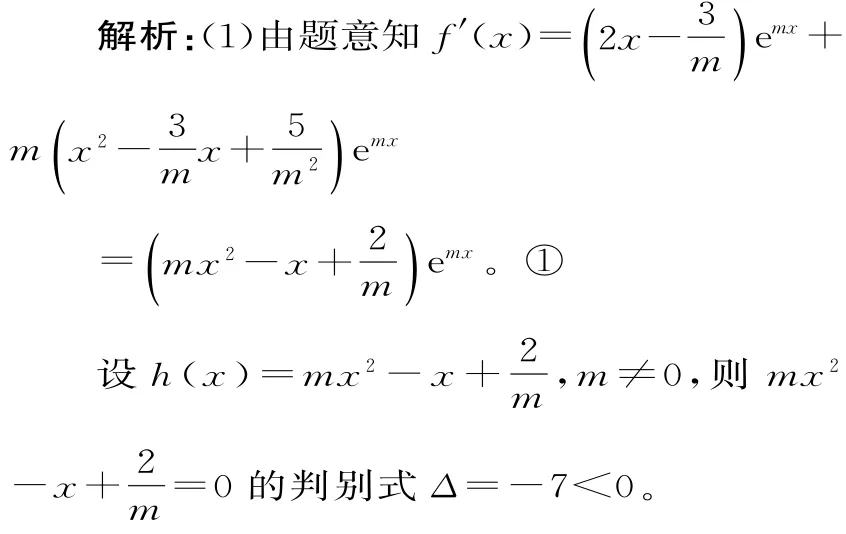
因此,當m＜0時,h(x)＜0,可得f'(x)＜0,此時f(x)在(-∞,+∞)上單調遞減;

當m＞0時,h(x)＞0,可得f'(x)＞0,此時f(x)在(-∞,+∞)上單調遞增。

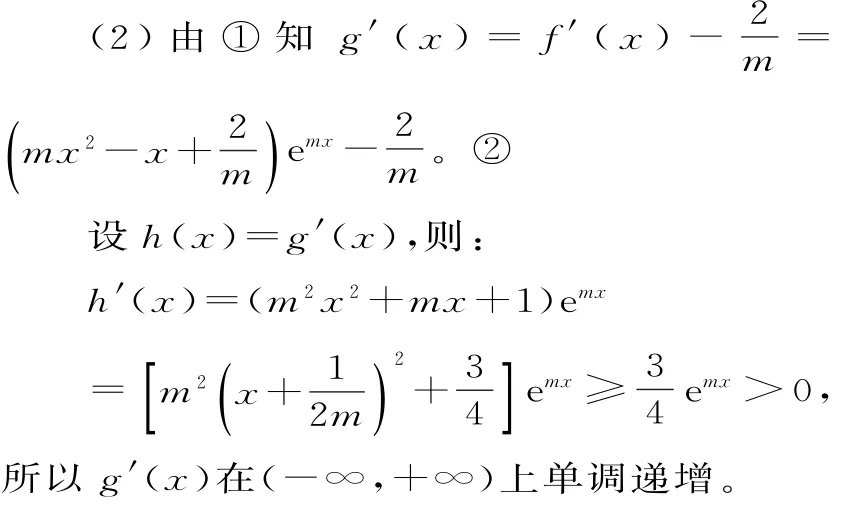
由②得g'(0)=0,所以當x＜0時,g'(x)＜g'(0)=0,g(x)在(-∞,0)上單調遞減;當x＞0時,g'(x)＞g'(0)=0,g(x)在(0,+∞)上單調遞增。

又g(0)＜0,g(x)在(-∞,0)上單調遞減,故g(x)在(-∞,0)上恰有一個零點。

另一方面,當x＞0時,emx＞1。

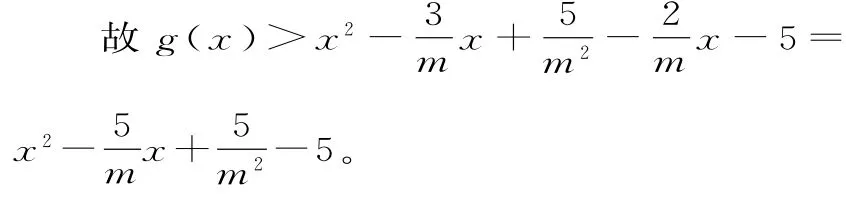
又g(0)＜0,g(x)在(0,+∞)上單調遞增,故g(x)在(0,+∞)上恰有一個零點。

從而當m＞1時,g(x)恰有兩個零點。

同理可證當m＜-1時,g(x)恰有兩個零點。

綜上可知,滿足題意的m的取值范圍是(-∞,-1)∪(1,+∞)。

(貴陽市2017屆高三上學期期末測試卷)已知函數f(x)=2a2lnx-x2(a＞0)。

(1)當a=1時,求曲線y=f(x)在點(1,f(1))處的切線方程;

(2)求函數y=f(x)的單調區間;

(3)討論函數y=f(x)在區間(1,e2)上零點的個數。

又因為f(1)=2ln1-12=-1,所以曲線y=f(x)在點(1,f(1))處的切線方程為y=-1。

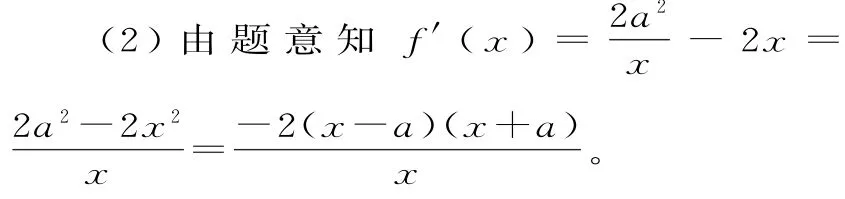
因為x＞0,a＞0,所以當0＜x＜a時,f'(x)＞0;當x＞a時,f'(x)＜0。

因此,f(x)在(0,a)上是增函數,在(a,+∞)上是減函數。

(3)由(2)得:

f(x)max=f(a)=a2(2lna-1)。

下面討論函數f(x)的零點情況。

①當a2(2lna-1)＜0,即0＜a＜e時,函數f(x)在(1,e2)上無零點。

②當a2(2lna-1)=0,即a=e時,函數f(x)在(0,+∞)內有唯一零點a,又1＜a=e＜e2,故函數f(x)在(1,e2)內有一個零點。

③當a2(2lna-1)＞0,即a＞e時,由題意知f(1)=-1＜0,f(a)=a2(2lna-1)＞0,f(e2)=2a2lne2-e4=4a2-e4=(2ae2)(2a+e2)。故當2a-e2＜0,即 e＜a＜時,1＜e＜a＜＜e2,f(e2)＜0,由單調性可知,函數f(x)在(1,a)內有唯一零點x1,在(a,e2)內有唯一零點x2,所以f(x)在(1,e2)內有兩個零點。

當2a-e2≥0,即a≥＞e時,f(e2)≥0,而且f(e)=2a2·-e=a2-e＞0,f(1)=-1＜0,由單調性可知,無論a≥e2還是a＜e2,f(x)在(1,e)內有唯一的一個零點,在(e,e2)內沒有零點,從而f(x)在(1,e2)內只有一個零點。

綜上所述,當0＜a＜e時,函數f(x)無零點;當a=e或a≥,函數f(x)有一個零點;當 e＜a＜,函數f(x)有兩個零點。

例3和例4是函數零點問題,運用數形結合思想是關鍵。在研究函數時,二次求導是常見的策略。函數零點個數的確定,往往要借助零點存在定理,使用零點存在定理的難點在于利用單調性后,區間內兩個函數值的乘積小于零的確定,往往要結合放縮法以確定函數值的符號。

三、證明不等式

(2016年廣州市一模理科數學卷)已知函數f(x)=ex+m-x3,g(x)=ln(x+1)+2。

(1)若曲線y=f(x)在點(0,f(0))處的切線斜率為1,求實數m的值;

(2)當m≥1時,請證明:f(x)＞g(x)-x3。

解析：(1)因為f'(x)=ex+m-3x2,所以f'(0)=em-3×02=1,解得m=0。

(2)f(x)＞g(x)-x3等價于ex+mln(x+1)-2＞0。

當m≥1時,ex+m-ln(x+1)-2≥ex+1-ln(x+1)-2。

所以要證ex+m-ln(x+1)-2＞0,只需證明ex+1-ln(x+1)-2＞0。

設h(x)=ex+1-ln(x+1)-2。

當x∈(-1,x0)時,h'(x)＜0;

當x∈(x0,+∞)時,h'(x)＞0。

故當x=x0時,h(x)取得最小值h(x0)。

所以h(x)≥h(x0)=ex0+1-ln(x0+1)

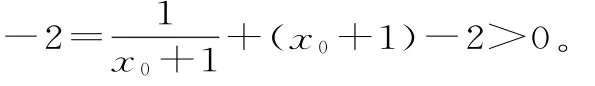
綜上所述,當m≥1時,f(x)＞g(x)-x3成立。

解析：由題意可知f(x)的定義域為(0,+∞)。

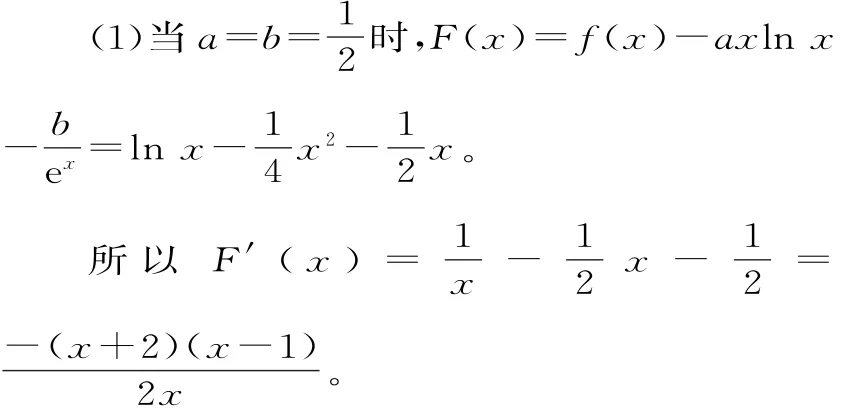
令F'(x)＞0,得0＜x＜1;

令F'(x)＜0,得x＞1。

所以F(x)的增區間為(0,1),減區間為(1,+∞)。

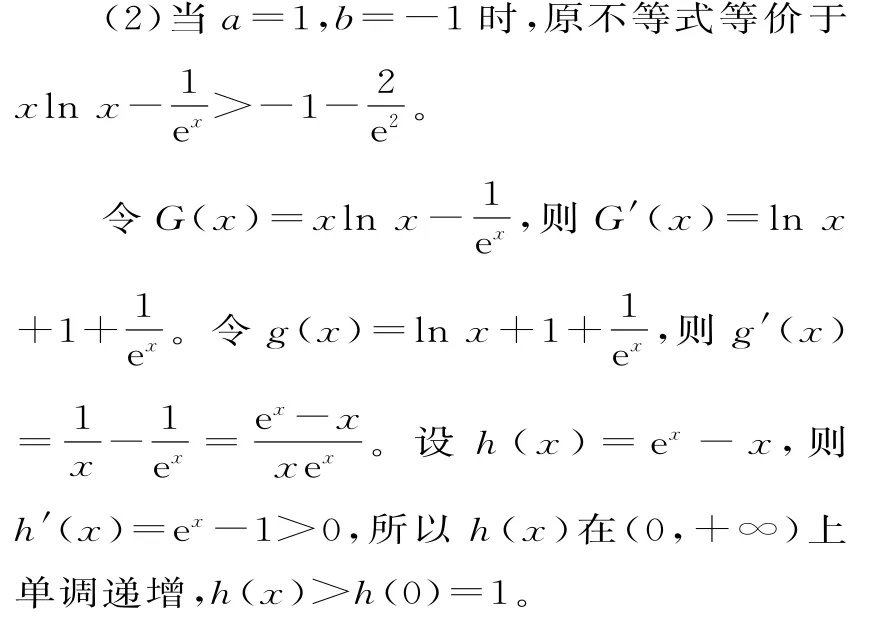
所以g'(x)＞0,g(x)在(0,+∞)上單調遞增。

當x∈(0,x0)時,g(x)＜0,G(x)單調遞減;當x∈(x0,+∞)時,g(x)＞0,G(x)單調遞增。所以G(x)≥G(x0)=x0lnx0-e-x0=x0lnx0+lnx0+1。

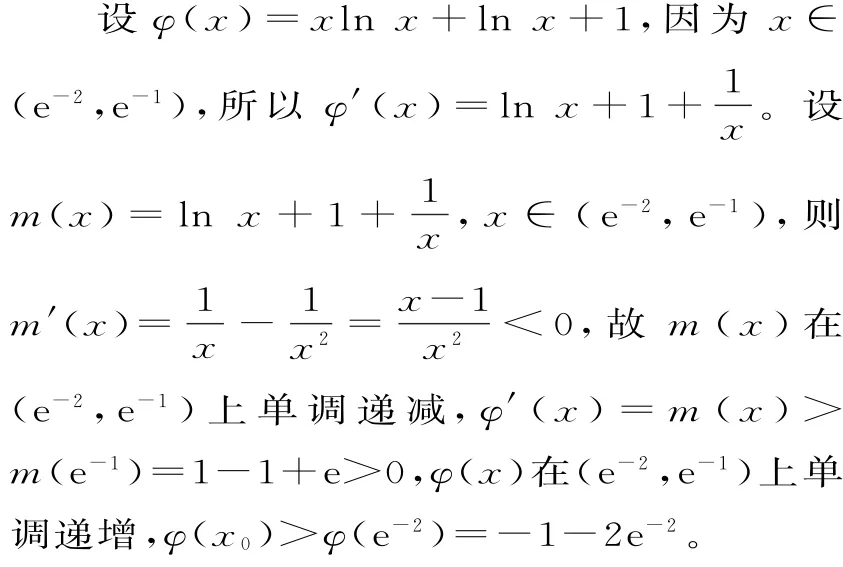
G(x)≥G(x0)=φ(x0)＞-1-2e-2。

例5和例6是高考中利用導數證明不等式的熱點問題,常見的做法是構造函數,通過函數的最值進行證明。試題通過作差構造函數,并通過多次求導,以確定函數的最值,但由于函數的極值點難以求解,故可借助設而不求,整體代換的技巧實現問題的解決。構造函數,借助導數證明不等式,除直接作差構造之外,還可通過下列技巧求解:

①分離參數后構造函數;

②通過代數變形(如取對數)后構造函數;

③換元構造,聲東擊西;

④構造雙函數,各個擊破;

⑤主元構造,定主略從;

⑥放縮構造,化繁為簡;

⑦多次構造,多次求導。

四、極值點偏移問題

(2016年甘肅省蘭州市高三診斷考試)已知函數f(x)=ex-ax-1(a為常數),曲線y=f(x)在與y軸的交點A處的切線斜率為-1。

(1)求a的值及函數y=f(x)的單調區間;

(2)若x1＜ln2,x2＞ln2,且f(x1)=f(x2),試證明:x1+x2＜2ln2。

解析：(1)因為f'(x)=ex-a,又f'(0)=1-a=-1,所以a=2。

故f(x)=ex-2x-1,f'(x)=ex-2。

由f'(x)＞0,得x＞ln2;由f'(x)＜0,得x＜ln2。

所以函數y=f(x)在(-∞,ln2)上單調遞減,在(ln2,+∞)上單調遞增。

(2)設x＞ln2,所以2ln2-x＜ln2,f(2ln2-x)=e(2ln2-x)-2(2ln2-x)-1=

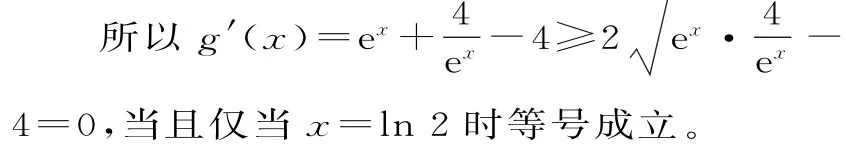
所以g(x)在(ln2,+∞)上單調遞增。

又因為g(ln2)=0,所以當x＞ln2時,g(x)=f(x)-f(2ln2-x)＞g(ln2)=0。故f(x)＞f(2ln2-x)。

因此,f(x2)＞f(2ln2-x2)。

又因為f(x1)=f(x2),所以f(x1)＞f(2ln2-x2)。

由于x2＞ln2,所以2ln2-x2＜ln2,又因為x1＜ln2,由(1)知函數y=f(x)在(-∞,ln2)上單調遞減,所以x1＜2ln2-x2。

因此,x1+x2＜2ln2,得證。

(1)討論f(x)的單調性。

(2)設a＞0,證明:當0＜x＜a時,f(a+x)＜f(a-x)。

(3)設x1,x2是f(x)的兩個零點,證明

解析：(1)由題意可知f(x)的定義域為(0,+∞)。

①若a≤0,則f'(x)＞0,此時f(x)在(0,+∞)上單調遞增;

②若a＞0,則由f'(x)=0得x=a,當0＜x＜a時,f'(x)＜0,當x＞a時,f'(x)＞0,此時f(x)在(0,a)上單調遞減,在(a,+∞)上單調遞增。

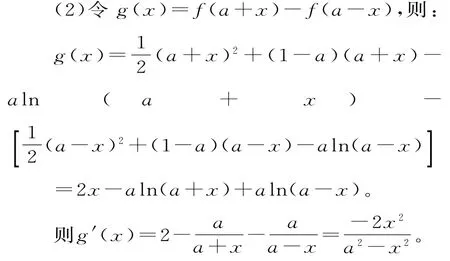
當0＜x＜a時,g'(x)＜0,所以g(x)在(0,a)上是減函數。

而g(0)=0,所以g(x)＜g(0)=0,故當0＜x＜a時,f(a+x)＜f(a-x)。

(3)由(1)可知,當a≤0時,函數y=f(x)至多有一個零點,故a＞0,從而f(x)的最小值為f(a),且f(a)＜0。

不妨設0＜x1＜x2,則0＜x1＜a＜x2,所以0＜a-x1＜a。

由(2)得f(2a-x1)=f(a+a-x1)＜f(x1)=f(x2)=0。

例7和例8是經典的極值點偏移問題,所謂極值點偏移問題,就是:已知函數y=f(x)是連續函數,f(x)在區間(x1,x2)內只有一個極值點x0,且f(x1)=f(x2),不少極值函數由于極值點左右的增減速度不同,函數圖像不具對稱性,常常有極值點x0≠的情況。解決這類問題首先應確定零點的大致范圍,從所證結論出發,構造差函數,結合函數的單調性與等量代換,實現問題的解決。