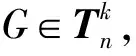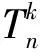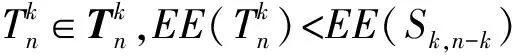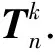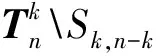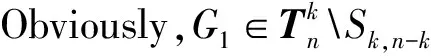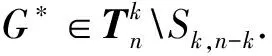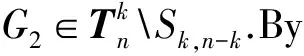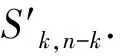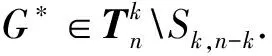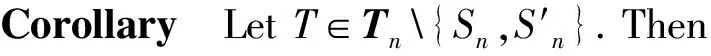On k-trees with Extremal Signless Laplacian Estrada Index and Estrada Index
, ,
(College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China)
All graphs considered in this paper are finite, undirected and simple. LetG=(V,E) be a connected graph, letNG(v)={u|uv∈E},NG[v]=NG(v)∪{v}. DenotedG(v)=|NG(v)| by the degree of the vertexvofG. IfW?V, letNG(W)=∪v∈WNG(v)W,NG[W] be the set of vertices within distance at most 1 fromW,G-Wbe the subgraph ofGobtained by deleting the vertices ofWand the edges incident with them. IfE0?E(G), we denote byG-E0the subgraph ofGobtained by deleting the edges inE0. IfE1is the subset of the edge set of the complement ofG,G+Edenotes the graph obtained fromGby adding the edges inE1: IfE={xy} andW={v}, we writeG-xyandG-vinstead ofG-{xy} andG-{v}, respectively. The joinG1∨G2of two edge-disjoint graphsG1andG2is obtained by adding an edge from each vertex inG1to each vertex inG2. For other undefined notations we refer to Bollobás[1].
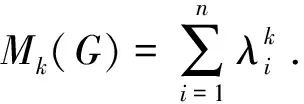
LetD=D(G)=diag(d(v1),…,d(vn)) be a diagonal matrix with degrees of the corresponding vertices ofGon the main diagonal and zero elsewhere, whered(vi) is the degree ofvi. The matrixQ=D(G)+A(G) is called the signless Laplacian ofG. SinceQis real symmetric and positive semi-definite matrix, its eigenvalues are real numbers. Letq1≥q2≥…≥qn≥0 are the signless Laplacian eigenvalues ofG. The multiplicity of 0 as an eigenvalue ofQis equal to the number of bipartite connected components ofG. The set of all eigenvalues ofQis the signless Laplacian spectrum ofG.
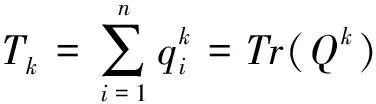
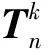
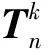
1 Preliminaries
In this section, we give some definitions and structure properties ofk-trees which will be used in the proof of our main results.
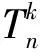
Lemma1[11]

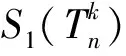
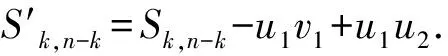
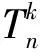
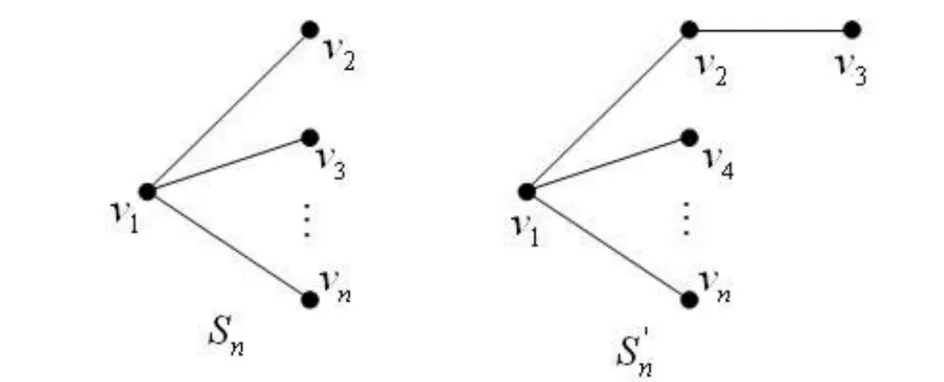
LetGandHbe two graphs withu1,v1∈V(G) andu2,v2∈V(H). IfMk(G;u1,v1)≤Mk(H;u2,v2) for all positive integersk, then we write (G;u1,v1)?M(H;u2,v2). If (G;u1,v1)?M(H;u2,v2) and there is at least one positive integerk0such thatMk0(G;u1,v1) Fig.1 The k-trees Sk,n-k and 圖1 k-樹(shù) Sk,n-k 和 Lemma3Letu,v∈V(G) andNG(v)?NG[u]. Then (i) (G;v)?M(G;u),and (G;w,v)?M(G;w,u) for eachw∈V(G) . Moreover, ifdG(v) (ii) (G;v)?T(G;u), and (G;w,v)?T(G;w,u) for eachw∈V(G)[12]. Moreover, ifdG(v) ProofWe only need to prove (i). Firstly, we prove (G;v)?M(G;u). LetWbe a walk inWk(G;v). Ifuis not inW, note thatNG(v)?NG[u], letf(W)=W′, whereW′ is the walk that is obtained by replacing the vertexvbyu, obviously,W′∈Wk(G;u) . Ifuis inW, we can also lookWas a walk which is starting and ending at vertexu, letf(W)=W. Obviously,fis an injection fromWk(G;v) toWk(G;u). Hence (G;v)?M(G;u). IfdG(v) (i) If (G;v)T(G;u), and (G;wi,v)?M(G;wi,u) for eachi=1,2,…,r,thenEE(Gv) (ii) If (G;v)T(G;u), and (G;wi,v)?T(G;wi,u) for eachi=1,2,…,r, thenSLEE(Gv) Lemma 4 is an excellent tool to deal with the extremal problems on Estrada index and signless Laplacian Estrada index, but it has many conditions which have to be provided when we want to use it.The lemma 3 enables us to discover a special case that provides such conditions. In this section, we will give a unified method to characterize thek-trees with the largest and second largest Estrada index and signless Laplacian Estrada index, respectively, which is simpler than the method provided in Ref[10]. Lemma5LetGbe a graph withvu,uw∈E(G) andvw?E(G). LetG′=G-vu+vw. IfNG(v)?NG[u], thenEE(G) ProofLetH=G-vu. ThenG=H+vu;G′=H+vwandNH(v)?NH[u]. Note thatw?NG[v], we havedH(v) Repeated by Lemma 5, we can obtain the following result. Lemma6LetGbe a graph andX={x1,x2,…,xt} be an independent set of equivalent vertices such thatxiu,uw∈E(G) andxiw?E(G) for 1≤i≤t. LetG′=G-{xiu,1≤i≤t}+{xiw,1≤i≤t}. IfNG(v)?NG[u], thenEE(G) ProofSince there exists a vertexv∈S1(G-S1(G)), letNG-S1(G)(v)={v1,v2,…,vk},UG(v)=NG(v)-NG-S1(G)(v). Then the vertices inNG-S1(G)(v) induce a complete graphKk; and the vertices inUG(v) which are all simplicial verices, induce an empty graph. For a vertexx∈UG(v), it is adjacent to all but one vertex inNG-S1(G)(v). LetUibe the set of vertices inUG(v) whose neighbour set isPG(v)=|{1≤i≤k,Ui≠?}|, where 1≤i≤k. For a vertexv∈S1(G-S1(G)), letv∈S1(G-S1(G)) andp(G)=min|{PG(v),v∈S1(G-S1(G))}|.Without loss of generality, letpG(u)=p(G),NG-S1(G)(v)={v1,v2,…,vk} andUG(u)=U1∪…∪Up(G)(as shown in Fig.2). Obviously, we haveNG[Ui]?NG[u] for 1≤i≤k. LetG′=G-{ux:x∈U1}+{v1x:x∈U1}. Fig.2 The structure of NG-S1(G)(v) and UG(u)圖2 NG-S1(G)(v)和UG(u)的結(jié)構(gòu) Note thatv1x?E(G). By Lemma 6, we haveEE(G) Fig.3 The structure of the graph G* in the proof in Theorem 9圖3 定理9證明中圖G* 的結(jié)構(gòu) LetV(G*)S1(G*)={v1,v2,…,vk+1} and |S1(G*-S1(G*))|={vk+1}. Further, letUG(vk+1)=NG(vk+1)-{v1,v2,…,vk};Uibe the set of vertices inUG(vk+1) whose neighbour set is {v1,…,vi-1,vi+1,…,vk,vk+1} for 1≤i≤k, andp=|{1≤i≤k,Ui≠?}| (as shown in Fig.3). Case3p=1 andS1(G*)-UG(vk+1)=?. This completes the proof. Fig.4 The graphs Sn and 圖4 圖Sn和 [1]Bollobás B. Modern graph theory[M]. Berlin, New York: Springer-Verlag, 1998. [2]Estrada E. Characterization of 3D molecular structure[J]. Chemical Physics Letters, 2000, 319: 713-718. [4]Ayyaswamy S K, Balachandran S, Venkatakrishnan Y B, et al. Signless Laplacian Estrada index[J]. MATCH - Communications in Mathematical and in Computer Chemistry, 2011, 66: 785-794. [5]Harary F, Palmer E M. On acyclic simplicial complexes[J]. Mathematika, 1968,15: 115-122. [6]Beineke L W, Pippert R E. The number of labeledk-dimensional trees[J]. Journal of Combinatorial Theory, 1969, 6(2): 200-205. [7]Estes J, Wei B. Sharp bounds of the Zagreb indices ofk-trees[J]. Journal of Combinatorial Optimization, 2014, 27: 271-291. [8]Wang S, Wei B. Multiplicative Zagreb indices ofk-trees[J]. Discrete Applied Mathematics, 2015, 180: 168-175. [9]Wang X X, Zhai M Q, Shu J L. Upper bounds on the spectral radius ofk-trees[J]. Applied Mathematics- Journal of Chinese Universities Series a, 2011, 26(2): 209-214. [10]Huang F, Wang S. On maximum Estrada indices ofk-trees[J]. Linear Algebra and Its Applications, 2015, 487: 316-327. [11]Song L, Staton W, Wei B. Independence polynomials ofk-tree related graphs[J]. Discrete Applied Mathematics, 2010, 158: 943-950. [12]Nasiri R, Elahi H R, Fath-Tabar G H, et al. The signless Laplacian Estrada index of tricyclic graphs [EB/OL]. [2013-11-30].http://arxiv.org/abs/1412.2280v2. [13]Du Z, Liu Z. On the Estrada and Laplacian Estrada indices of graphs[J]. Linear Algebra and Its Applications, 2011,435: 2065-2076. [14]Ellahi H, Nasiri R, Fath-Tabar G, et al. On maximum signless Laplacian Estrada indices of graphs with given parameters[EB/OL]. [2013-11-30]. http:// arXiv:1406.2004v1.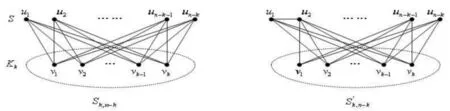
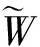
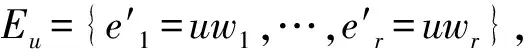
2 Main results