面向瞬態成像仿真的遮擋目標逆向重構方法

李海瑞， 吳　鑫， 張建奇

(西安電子科技大學 物理與光電工程學院，陜西 西安 710071)

瞬態成像(Transient Imaging，TI)是一種新穎的成像方式．瞬態成像源于上世紀70年代末由文獻[1]完成的“飛光記錄”(Light-in-Flight)研究，其提出了利用皮秒級激光照明場景并進行全息記錄，能夠對某一特定時刻的波前進行光學重建．盡管重建場景的復雜度受全息設備性能的限制，但其他研究者已經利用這一方法進行了可見場景三維幾何結構測量的工作[2]，形成了瞬態成像的概念．在瞬態成像過程中，短脈沖激光在遍歷完場景并達到光能分布平衡之前，就會以很高的時間分辨率被探測到．因此，得到的瞬態圖像是一系列表示場景對脈沖響應的時序圖像．

隨著超快成像器件的高速發展，一個更簡單高效的成像方式被提了出來，被稱為瞬態成像框架(Transient Imaging Framework)[3]．該框架的成像設備由一個飛秒級激光器和一個條紋相機組成，其中飛秒級激光器作為主動脈沖照明源，條紋相機用于捕獲場景對脈沖響應的時序圖像．這一項新的成像方式催生出了很多新的應用，如重建被遮擋場景的幾何結構、獲得物體的表面反射率、復雜場景中光傳輸的可視化[4]以及透明物體的深度探測等．遮擋重構是一個重要的研究領域，圖像的形成過程十分復雜，既包含可見物體的直接反射，還包括遮蔽物體的間接散射．如何把這些反射分離開來，是一個巨大的挑戰．目前的重構方案仍然是以文獻[5-7]所提出的方法為基礎，他們利用一個嚴格控制的實驗室設備演示了遮擋重構的過程．盡管重構結果沒有使用到場景先驗假設，但是卻依賴于一個昂貴的定制設備，從而具有很大的局限性．近年來，其他研究者相繼提出了兩種更廉價的瞬態成像設備[8-9]，盡管可能犧牲一定的時間和空間分辨率，卻對推動瞬態成像技術的商業化應用具有重要的意義．由于瞬態成像的基礎理論尚未完全建立，目前的工作中仍然存在一些問題難以回答．文獻[10-11]利用信號處理方面的理論對重構過程進行了詳細分析，指出可以利用信號處理方面的理論和方法提高重構質量．

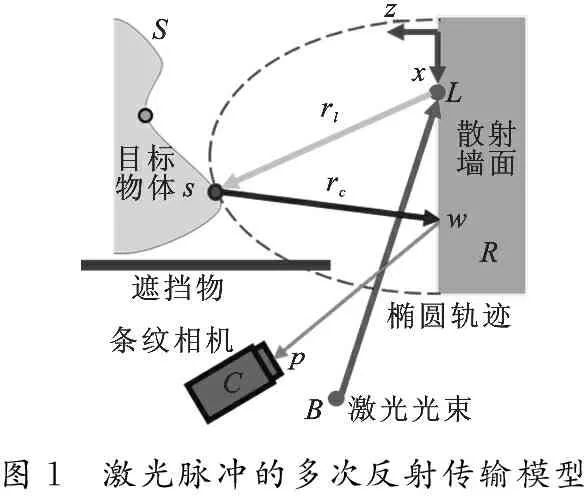
圖1 激光脈沖的多次反射傳輸模型

筆者利用文獻[12]提出的一個瞬態渲染框架獲得場景響應的仿真數據．針對瞬態成像中實際硬件水平的不足和實驗的復雜性，改進了原有框架的逆向重構算法．利用軟件仿真的手段將瞬態成像過程進行可視化分析，提高了目標重構的效果．

1　逆向重構算法的簡化

圖1是描述了一束激光在場景中傳輸的物理模型．首先，由激光器B發出的一束脈沖光到達散射墻面R上的點L；然后，光從點L處向四周散射，其中有一小部分沿路徑rl到達了未知表面S上的點s；接著，光從點s處再次向四周散射，其中有一小部分沿路徑rc到達了散射墻面R上的點w；最后，光從點w又一次向四周散射，其中一小部分到達條紋相機C中的像素p上，并被探測到．逆向重構的任務是通過對反射光線的計算，獲得被遮擋表面S的幾何信息，又稱為繞射探測或遮擋成像．

1.1　逆向重構算法

逆向重構算法包括兩個計算過程: 工作空間體素化和逆向投影．假設在空間中存在一個完全包圍未知表面S的長方體空間，記為工作空間V，把工作空間V均勻地劃分為一系列邊長相等的立方體，并稱之為體素，記為v．記激光器發射激光脈沖為時間原點，t=0．由圖1可知，在t時刻，只有滿足以下條件的體素v才對點w處有光強貢獻:

ct=|L-B|+|v-L|+|w-v|+|p-w|．

(1)

由于散射墻面R是可見場景，條紋相機C和激光器B的設置已知，因此，變量ct，|L-B|，|p-w|都是可知的．所以有

|v-L|+|w-v|=d,d=ct-|L-B|-|p-w|．

(2)

這是一個以點L和點w為焦點、長軸為d的橢球面，稱滿足該式關系的p,w,v為互相貢獻關系．

對于工作空間V中的每一個體素v，按如下方式計算一個關于v的像素累積函數H:

(3)

其中，p是所有與體素v為互相貢獻關系的像素；Ip為像素p處探測到的光強；a為一常數因子，通常取a=1．

1.2　逆向重構算法的簡化

將像素累積函數式(3)簡化為

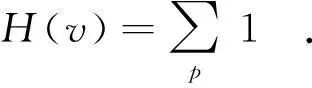
(4)

即對于每個體素v，其所有的貢獻像素p對函數H的貢獻值相同，皆取值為1．這意味著重構過程中Ip的大小并不重要，只需記錄體素在光的傳播過程有無響應．因此，在重構過程中就不必反復計算探測到光強的大小，而只需要判斷能否探測到光強即可，從而可以極大地簡化重構過程的復雜度，提高了算法的處理效率．

從式(2)可以看出，在t時刻，對點w有光強貢獻的體素不是惟一的．式(2)確定了一個可能體素的候選范圍，即由式(2)確定的一個橢球面．假設光的衰減只與其傳播距離有關，即滿足Ie=Is/r的關系．圖2(a)描述了當點s在由點L和點w確定的橢圓軌跡上移動時，光經過光路rl和rc的衰減程度 |rl| |rc| 是不同的．但是點L處的光強IL卻是相同的，因而到達點w的光強Ip=IL/ (|rl| |rc|) 就會不同．利用式(3)計算，恰好消除了經過不同光路衰減程度不同的問題，得到相同貢獻的光強IL．因此，在這一點上，式(4)和式(3)是完全等價的．

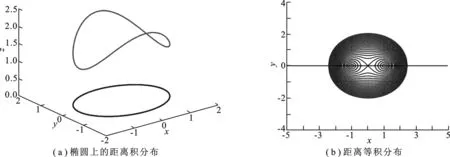
圖2　距離積分布圖

但是實際上由式(2)確定的橢球面上只有一個點s對點w有光強貢獻，即光路是惟一的，光強的衰減程度是惟一的．但當按照式(3)對式(2)確定的橢球面上所有的可能點s計算時，同樣大小的Ip卻因為體素v的空間位置不同，而對H的貢獻大小不同．在xy平面中取兩個定點F1,F2，其坐標分別為 (-c, 0)，(c,0)，這里取c=1．設點f為平面內的任意一點．按下式可以得到一個距離等積曲線:

|f-F1| |f-F2|=a1，

(5)

其中，a1為一個常數．當a1從0逐漸增大時，距離等積曲線的分布如圖2(b)所示．由圖2(b)可以看出，距離等積曲線的分布不是各個方向均勻的．當a1≈c時，靠近線段F1F2的中垂線的體素v對函數H的貢獻更大; 當a1?c時，逐漸接近均勻．這說明利用式(3)進行重構時，可能會使結果具有一定的空間差異性．

當把式(3)簡化為式(4)后，重構問題就會完全歸結為一個概率統計的問題．對重構問題的分析和研究會變得更加簡單．

2　逆向重構算法的補充

在對逆向重構算法進行簡化的基礎上，筆者提出了一種與其相適應的取樣模式，可以加快重構結果的收斂速度．在描述取樣模式之前，首先利用檢測概率[13]的概念給出逆向重構算法的概率意義．設v為工作空間V內的任意一個體素，w為散射墻面R上的任意一點，定義事件A(v,w)為在點w處檢測到體素v．在這里，由式(2)和式(4)可得

(6)

設W為相機在散射墻面R上的可探測范圍，w∈W，對應的函數H記為HW．對HW進行歸一化處理:

(7)

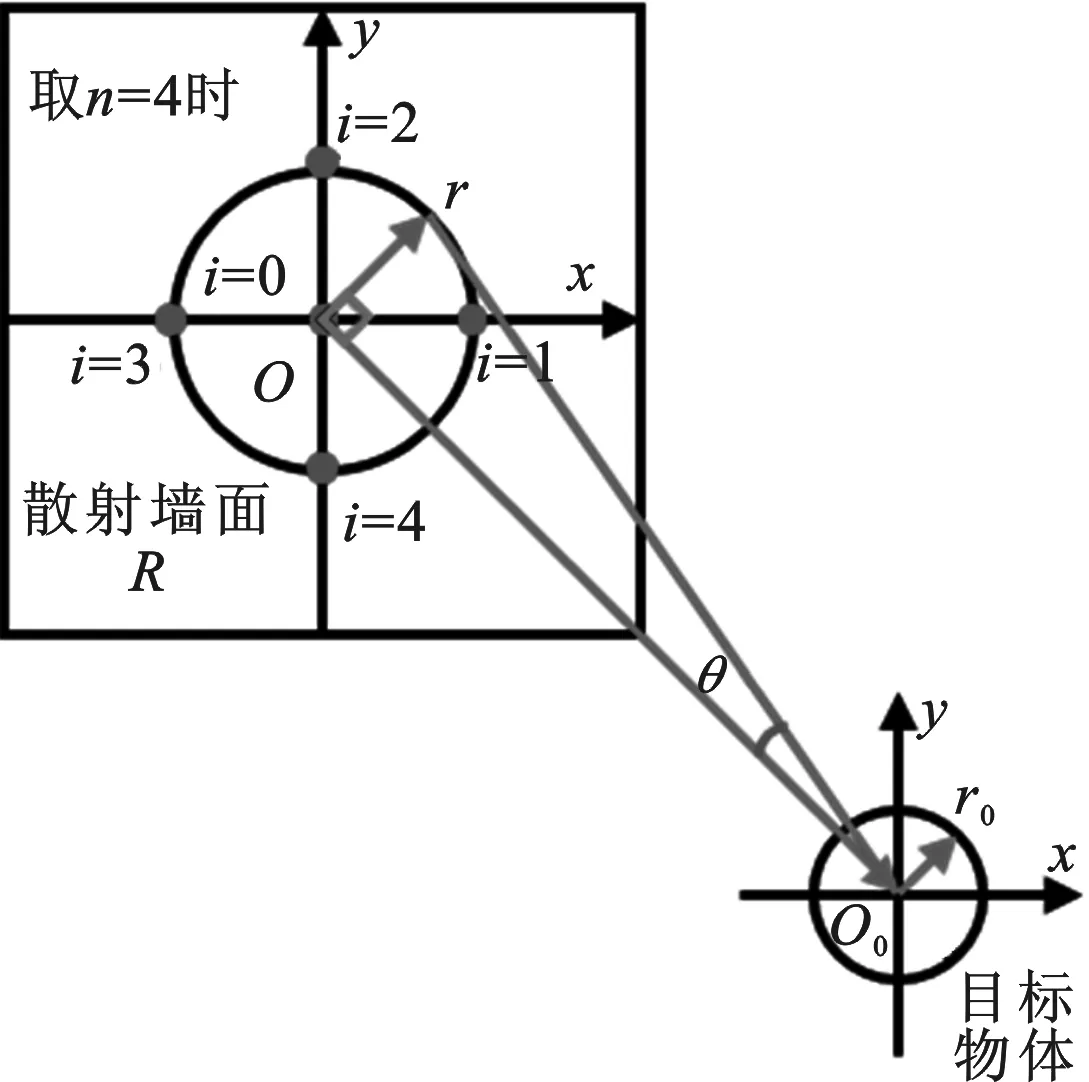
圖3　取樣過程示意圖

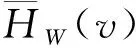
采用如圖3所示的取樣模式．

直接利用上面描述的逆向重構算法，可以得到一個目標物體的粗略重構結果，進而對目標物體的中心位置O0做出一個估計．調整圖3中的圓心O，使直線OO0垂直于散射墻面R．要求 |w-L|?r，接下來描述時，把點w和點L簡化為一點，即點W．規定點W只能取圖3中圓心O和圓周上的位置．以點(r,0)為第1個n等分點，按逆時針方向，順序得到圓周上第i(i=1，2，…，n)個n等分點(要求n≥3)．記在圓周的第i個n等分點位置處按式(4)得到的函數H為Hi．特別地，圓心O處得到的函數H記為H0．

改進后的逆向重構算法可以按以下步驟實現:

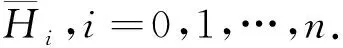
(8)

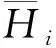
(3) 閾值分割．經過匯總之后，Hcircle已經收斂了，為了獲得比較好的顯示效果，可以選取一個較小的閾值對結果進行分割，閾值的選取如下:

Hthresh=β·max{Hcircle(v),v∈V},

(9)

其中，β是一個常數因子．取β=0.001～0.010，可以得到較好的結果．

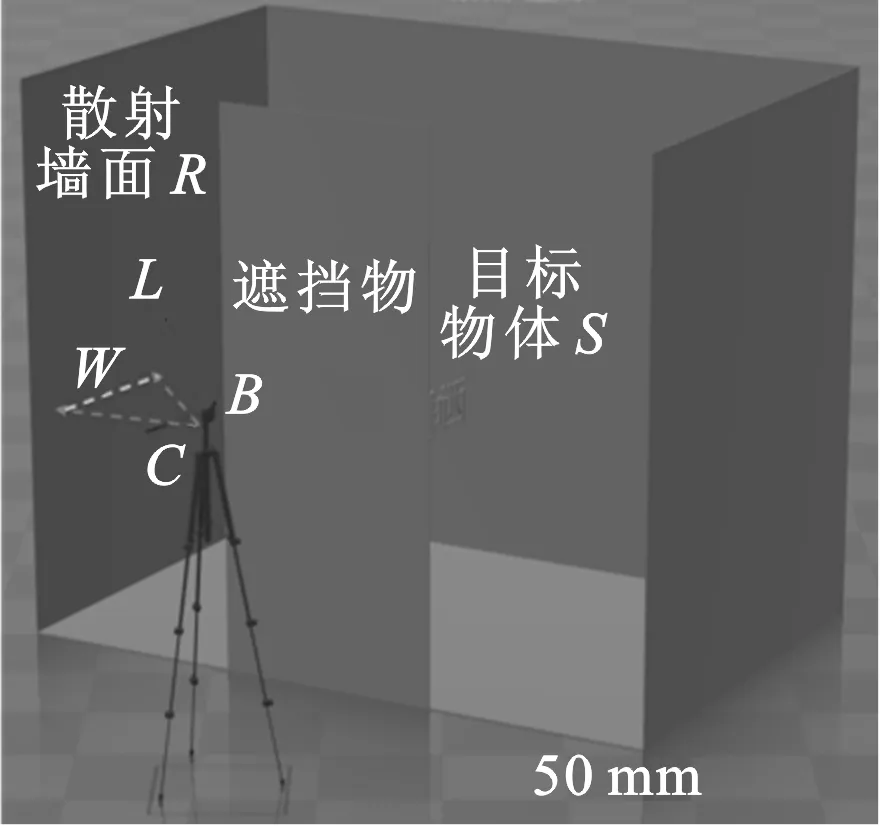
圖4　仿真場景布局

3　重構結果與分析

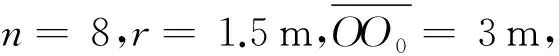
圖5　重構結果的三維顯示

圖6　重構結果的二維顯示

3.1　重構結果的可視化顯示

分別以漢字“西”和“電”作為待重構目標的重構結果的三維顯示如圖5所示．灰色點代表重構點，白色點是利用其他方法得到的原模型的點云，作為對比．重構結果的二維顯示如圖6所示．圖6(a)中的灰度大小表示式(8)中計算的Hcircle的相對大小．圖6(b)為圖6(a)的二值化顯示．

3.2　對重構結果的分析

記實際包含待重構物體表面點的體素點為“真點”，否則為“假點”．由式(2)可知，雖然該式把“真點”的范圍從整個工作空間限制到了一個橢球面上，但橢球面上包含“真點”的同時，必然包含很多“假點”．因此，僅僅依靠式(6)雖然可以重構出“真點”，但必然引入大量的噪聲．值得注意的是，由式(2)引入的“假點”受橢球面的位置和形狀的影響遠遠大于“真點”．因此可以通過改變橢球面的形狀和位置得到多組重構結果，然后結合這些結果達到抑制噪聲的目的．上文的取樣模式正是基于這一點提出的．由重構結果可知，通過該方法確實可以有效地抑制噪聲，從而加快重構處理過程．需要指出的是，筆者提出的取樣模式在有效地抑制噪聲的同時，也會對一部分“真點”進行抑制．理論上，這種抑制幾乎不會造成目標物體的信息丟失; 但實際上，由于取樣量少的原因，每組均會有部分“真點”遺漏，最終造成匯總結果損失部分信息．因此，每組取樣的量必須足夠大，特別是如圖3中圓周上的位置，需要進行多次重復取樣，以減少信息丟失．

4　結 束 語

筆者改進了瞬態成像中的逆向重構算法，基于文獻[12]提出的瞬態渲染框架，通過軟件仿真的方法實現了被遮擋物體幾何結構的重構．仿真結果顯示，改進后的逆向重構算法不僅大大簡化了處理過程，而且取得了更好的重構效果．文中的仿真方法與結果有助于深入探索光的傳輸過程，并且對超高速成像系統的設計與測試也有指導意義．

參考文獻：

[1] ABRAMSON N. Light-in-flight Recording by Holography[J]. Optics Letters, 1978, 3(4): 121-123.

[2]NILSSON B, CARLSSON T E. Direct Three-dimensional Shape Measurement by Digital Light-in-flight Holography[J]. Applied Optics, 1998, 37(34): 7954-7959.

[3]KIRMANI A, HUTCHISON T, DAVIS J, et al. Looking around the Corner Using Ultrafast Transient Imaging[J]. International Journal of Computer Vision, 2011, 95(1): 13-28.

[4]VELTEN A, WU D, MASIA B, et al. Imaging the Propagation of Light through Scenes at Picosecond Resolution[J]. Communications of the ACM, 2016, 59(9): 79-86.

[5]VELTEN A, WILLWACHER T, GUPTA O, et al. Recovering Three-dimensional Shape around a Corner Using Ultrafast Time-of-flight Imaging[J]. Nature Communications, 2012, 3(2): 745.

[6]GUPTA O, WILLWACHER T, VELTEN A, et al. Reconstruction of Hidden 3D Shapes Using Diffuse Reflections[J]. Optics Express, 2012, 20(17): 19096-19108.

[7]RASKAR R, VELTEN A. Methods and Apparatus for Imaging of Occluded Objects from Scattered Light: US9148649[P]. 2015.

[8]HEIDE F, HULLIN M B, GREGSON J, et al. Low-budget Transient Imaging Using Photonic Mixer Devices[J]. ACM Transactions on Graphics, 2013, 32(4): 1-10.

[9]BUTTAFAVA M, ZEMAN J, Tosi A, et al. Non-line-of-sight Imaging Using a Time-gated Single Photon Avalanche Diode[J]. Optics Express, 2015, 23(16): 20997-21011.

[10]KADAMBI A, ZHAO H, SHI B, et al. Occluded Imaging with Time-of-flight Sensors[J]. ACM Transactions on Graphics, 2016, 35(2): 2836164.

[11]BHANDARI A, RASKAR R. Signal Processing for Time-of-flight Imaging Sensor: an Introduction to Inverse Problems in Computational 3-D Imaging[J]. IEEE Signal Processing Magazine, 2016, 33(5): 45-58.

[12]JARABO A, MARCO J, MUNOZ A, et al. A Framework for Transient Rendering[J]. ACM Transactions on Graphics, 2014, 33(6): 1-10.

[13]徐軍, 周翔, 梁昌洪. 一種計算紅外點目標檢測概率的方法[J]. 西安電子科技大學學報, 2001, 28(1): 18-21.

XU Jun, ZHOU Xiang, LIANG Changhong. Calculation of the Detecting Probability of an Infrared Point Target[J]. Journal of Xidian University, 2001, 28(1): 18-21.