基于拓撲優化的FSAE賽車車架結構設計

吳佳秜，張詩博*，解紫婷，陳浩杰

（1.成都農業科技職業學院機電技術分院，四川 成都 611130；2.南昌大學，江西 南昌 330031）

引言

近年來，中國對汽車工業發展愈加重視，電動方程式賽車車隊的要求便不僅僅局限于造出一輛的車，而著眼于打造一輛性能優異的賽車。車架作為一輛車受力、傳導力的重要結構部件，便對其有了更高的性能要求。本文主要著重于車架的設計與拓撲優化，把如何設計一個兼顧輕量化與安全性的車架作為本文研究的目標。

拓撲優化中的連續體拓撲優化對于桁架結構比較適用。連續體拓撲優化把定義空間分割成有限個單元進行設計，WEI K L[1]利用連續體拓撲優化中的變密度法對半掛車車架進行優化設計對變密度法進行了詳細討論，并給出了優化結果。CHEN C F[2]等對抑制棋盤格現象而引入的懲罰因子ρ作了描述，對結果進行的驗證也證明了其可靠性。

本文對FSAE賽車桁架式車架采用連續體拓撲優化的方法，建立有限個PSHELL單元和PBEAM單元的拓撲優化模型，借鑒與優化結果設計出兼顧輕量化與安全性的新車架，再對新車架進行力學及模態分析，保證車架結構滿足設計要求，可以安全參賽。

1　車架初步設計與建立有限元模型

1.1　車架初步設計

在CATIA軟件中建立了車架的最初模型。由于本車架采用鋼管桁架結構，故車架的設計從鋼管型號選擇，桁架空間結構設計，人機工程等方面考慮。本文初步設計的車架依據規則要求以及理論分析使用三種不同尺寸的 4130Cr鋼（彈性模量 E = 2.11×105MPa，泊松比μ=0.279，密度ρ=7850kg/m3，屈服強度σs(MPa)=785，初步車架的總質量約為40Kg），人機工程則根據CATIA人機工程學模塊與1: 1PVC管模型進行設計。

1.2　有限元模型的建立

有限單元法（FEM）是一種可以精確預測復雜結構在外界載荷作用下響應的方法，分析步驟分為：前處理、求解、后處理。本文將使用有限元分析的方法進行車架結構的設計。將CATIA模型導入至有限元分析軟件HyperWorks中，利用Hypermesh對其進行前處理。由于車架屬于桁架結構，故使用1D梁單元進行網格的劃分[3-4]。為減少計算量，在車架重要結構上，使用尺寸較小的單元進行劃分，尺寸為5mm，對于受力較小的部分使用尺寸較大的單元劃分，尺寸為10mm，網格的好壞直接決定結果的精確性，故在劃分完成后需仔細檢查網格質量。在劃分網格時，經常會由于網格不連續帶來的求解失敗或者結果很差，所以本文使用CATIA軟件中的創成式曲面設計模塊把所有桁架結構所有交點進行打斷，然后在 Hypermesh中的 Edges面板點擊 preview equiv再點擊equivalence，可以查找并閉合所有大節點，得到較優的梁單元網格。在網格劃分時注意梁單元的方向性，有利于求解出正確的結果。

圖2　連續的梁單元網格Fig.2 Continuous tube element mesh

2　初步車架剛度與自由模態分析

2.1　剛度分析

衡量車架力學性能指標的兩個重要因素為彎曲剛度與扭轉剛度[5]，剛度過低則容易造成車架在行駛過程中有較大的變形，不利于賽車的操控性，而且形變過大容易造成金屬疲勞，安全性能下降。剛度過高則不利于整車輕量化。參照國內外高水平車輛，一般來說，扭轉剛度在1000～5000 N·m/(o)左右，彎曲剛度在50000～150000 N·m/(o)左右為較優性能。本文加載的邊界條件為：固定后懸架硬點全部六個自由度，對前懸左右硬點分別施加5000N的方向相反的力以及5000N方向相同的力[6]。

圖3　初步車架的扭轉云圖Fig.3 The preliminary frame of the reverse figure

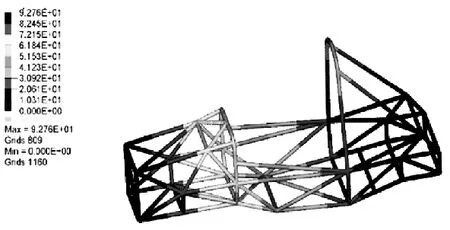
圖4　初步車架的彎曲云圖Fig.4 The frame curve displacement diagram

圖為初步車架扭轉位移圖與彎曲位移圖，可得到扭轉剛度為：4870 N·m/(o)彎曲剛度為：98580 N·m/(o)[7]，發現扭轉剛度過高。

2.2　自由模態分析

表1　初步車架固有頻率表Tab.3 Natural frequency of the frist frame table

通過Hyperworks軟件對初步車架進行自由模態分析，求解出初步車架前12階模態頻率，觀察結果發現前六階頻率數量級非常小，可近似看為剛體振型[8]，后六階頻率與振型如表所示。得到的扭轉剛度、彎曲剛度、固有頻率作為參照組與拓撲優化后的車架參數進行對比。

3　拓撲優化分析

3.1　拓撲模型的建立

依據對初步車架的有限元分析結果的研究，為了簡化拓撲分析的模型，在 CATIA軟件中對受力較差的結構進行刪除，保留基本結構以及受力較為優良的管件，再依據這些管件生成一個類似于單體殼的一個由面包絡的車架，僅保留主環前環等規則限定結構。導入至Hyperworks軟件中，選擇求解器時我們選擇 OptiStruct求解器，因為在處理多工況下的拓撲優化時，此求解器采用的為加權線性法[9]，在求解結果文件中我們可以看到不同的工況所占權重，對此進行調整，循環進行求解。在此求解器中定義包絡的面為拓撲設計空間，其余為非設計空間。使用2D PSHELL單元對設計空間進行網格劃分[1]，定義網格為矩形，由于為需優化結構，單元尺寸可適當縮小為10mm，厚度為8mm，再使用1D 梁單元對非設計空間進行網格劃分，由于為非優化結構，單元尺寸可適當放大為 15mm。建立車架的拓撲優化模型。該模型包含36457節點，36105個單元。

3.2　設計變量的創建

由于車架的扭轉剛度往往是考量車架性能的重要指標，故在施加載荷與約束時，我們先施加多種常見的的扭轉方式去求解初步分析結果。再對結果進行考量，觀察結構是否合理等，再添加其他的約束條件，如此不停反復修改，最終達到一種合理的結構，如圖5所示。

在創建完邊界條件之后，需要定義一個設計變量，包括最大化剛度以及最小化質量。在 OptiStruct中最大化剛度是以最小化柔度來體現的[9]。柔度C可以以以下關系式得到：

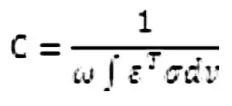
圖6　拓撲優化流程Fig.6 Topology optimization process

其中，柔度C是結構的應變能，可以認為柔度是剛度的倒數。在本文中，柔度指定為與全部工況相關，來求解最大化剛度，因為最大化剛度不能以一個數值體現[9]，求解結果是發散的，所以巧妙地使用剛度的對立面柔度來體現。在創建最大化剛度這一個響應中，針對不同的工況可以使用Weighted comp面板依據經驗對多個工況加權處理，在創建最小化質量這一個響應中，分析后發現取質量分數為0.21使可以得到更好結果。在設置成員尺寸時，經過不斷地嘗試，發現最小成員尺寸設置為 50mm，最大成員尺寸為最小成員尺寸為最小成員尺寸的兩倍即100mm時可以得到更好結果。

3.3　拓撲優化結果與分析

分析中我們創建了純扭轉工況、彎曲與扭轉復合工況、轉彎與彎曲復合工況。

圖7　純彎曲拓撲優化結果Fig.7 Topology optimization results of Torsion

圖8　扭轉與彎曲拓撲優化結果Fig.8 Topology optimization results of torsion and bending

圖9　扭轉與轉彎拓撲優化結果Fig.9 Topology optimization results of torsion and turn

圖6是在純扭轉工況下經過42次迭代求解的結果，分析發現，此工況下除后艙外形成了較為明顯的材料分布，前艙和座艙輪廓清晰。圖7是扭轉與彎曲的復合工況經過30次迭代求解的結果，對比圖 6，出現了較為明顯的后艙結構，主環斜撐支撐也出現了，這與初步車架彎曲剛度的有限元分析顯示的應力在此處較大的結果一致，表明此拓撲優化模型有很大的可信度。圖8是轉彎與扭轉的復合工況經過32次迭代求解的結果，分析發現，在后艙出現了明顯的底板結構，在后懸安裝點上材料分布比較密集，故設計時可以使用更高規格的鋼管。

3.4　車架結構的重新設計

分析以上三種結果可知，由于求解為最大剛度，故很多地方出現了交叉結構，雖然這有利于大大提升車架剛度，但非常不利于車架輕量化，故重新設計時我們簡化為單根支撐桿件。對于材料分布較少的地方我們使用低規格的鋼管，對于材料分布密集的地方我們使用高規格的鋼管，則新車架的鋼管類型改進到了7種規格。改進后的車架結構如圖9所示。

優化后車架的質量降低為30Kg，對于車架的輕量化起到非常有利的作用。

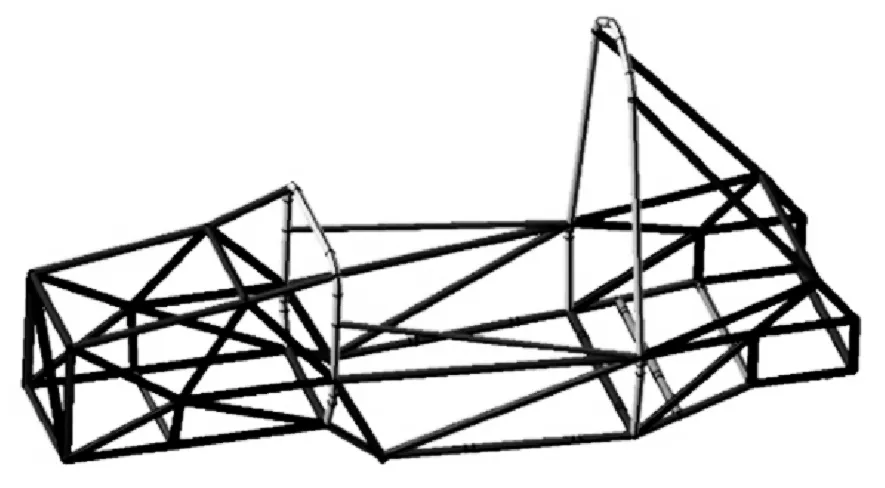
圖10　新車架三維模型Fig.10 The new frame 3D model

表2　新車架鋼管規格表Tab.1 The new frame steel pipe specification table

4　優化后的車架分析

4.1　剛度分析

圖11　新車架彎曲位移云圖Fig.11 The new frame curve displacement diagram

圖12　新車架扭轉位移云圖Fig.12 The new frame torsional displacement diagram

圖11與圖12為新車架扭轉與彎曲位移圖，可得到扭轉剛度為：3520N·m/(o)彎曲剛度為：86438 N·m/(o)[10]，由此可見，新車架剛度在允許范圍內略有下降。

4.2　自由模態分析

圖13　新車架第7階振型Fig.13 The new frame 7 order vibration mode

圖14　新車架第8階振型Fig.14 The new frame 8 order vibration mode

圖15　新車架第9階振型Fig.15 The new frame 9 order vibration mode

圖16　新車架第10階振型Fig.16 The new frame 10 order vibration mode

圖17　新車架第11階振型Fig.17 The new frame 11 order vibration mode

圖18　新車架第12階振型Fig.18 The new frame 12 order vibration mode

將新車架在Hyperworks軟件中進行自由模態的分析，求解出車架前12階模態頻率，觀察結果發現前六階頻率數量級非常小，可近似看為剛體振型[11]，后六階頻率與振型如下表所示。

表3　新車架固有頻率表Tab.3 Natural frequency of the new frame table

4.3　與優化前車架對比

表4　車架固有頻率對比表Tab.4 Contrast the natural frequency of the frame table

表5　車架剛度對比表Tab.4 Frame stiffness contrast table

圖19　使用新車架的賽車Fig.19 Use the new frame of the racing car

經過對比后發現，在拓撲優化后的車架在低階固有頻率上得到了較多提升，在高階固有頻率上得到了略微下降，這非常有利于使車架避開地面帶來的低頻率響應與電機帶來的高頻率響應，從而避免發生共振[12]。在彎曲剛度與扭轉剛度這兩個評判車架力學性能指標上雖然有一些下降，但在輕量化上面得到顯著提升。下圖為賽車的實物圖，車架得到了實際的檢驗。

5　結論

本文使用CATIA軟件以及Hyperworks軟件對FASE方程式賽車車架進行設計、分析、優化，最終加工出來的車架經過比賽的考驗得到了實際的驗證，得到了以下結論：

（1）車架前期設計很重要，合理的初步設計有利于提高拓撲優化結果的準確性。

（2）經過拓撲優化后，車架質量從40Kg降低為30Kg，提升了賽車整體性能，保證了賽車的操控穩定性。

（3）前五階模態的結果相比于初始車架平均提升了20%，車架的安全性也得到了提升。引入尺寸優化等新設計方法將是本文今后的研究方向。

[1] 魏顯坤,米林,萬鑫銘,等.基于Optistruct的鋁合金半掛車車架結構拓撲優化設計[J].四川兵工學報, 2012: 86-89.

[2] 陳垂福,藍雙,楊曉翔,等.基于SIMP理論的衡器載荷測量儀懸臂梁拓撲優化研究[J].機電工程, 2016: 383-387.

[3] 桂良進,周長路,范子杰.某型載貨車車架結構輕量化設計[J].汽車工程, 2003: 403-406.

[4] 齊益強,周冠男,李涵武.FSAE競賽車車架有限元靜力學分析[J].黑龍江科技信息, 2013: 55-56.

[5] 趙帥,隰大帥,王世朝,等. FSAE賽車車架的強度和剛度分析[J].計算機輔助工程, 2011: 53-56.

[6] 鄭文杰,蘭鳳崇,陳吉清. FSAE賽車車架結構拓撲優化及輕量化設計研究[J].汽車工程學報, 2016: 35-42.

[7] 彭倩,韓鋒鋼,洪漢池,等. FSAE賽車車架剛度特性分析[J]. 廈門理工學院學報, 2014: 7-11.

[8] 陳志勇,史文庫,沈志宏,等. 輕型客車車身車架整體結構有限元模態分析[J].振動與沖擊, 2010: 244-246, 263.

[9] 范文杰,范子杰,蘇瑞意. 汽車車架結構多目標拓撲優化方法研究[J].中國機械工程, 2008: 1505-1508.

[10] 于國飛,黃紅武,吳俊輝. 基于有限元的FSAE賽車車架的強度及剛度計算與分析[J].廈門理工學院學報, 2009: 29-32.

[11] 高棱,潘錦強,謝楚森,等.基于 ANSYS的 FSAE車架模態分析與驗證[J].煤礦機械, 2016: 172-174.

[12] 郭福森,洪漢池,陳志軍,等.FSAE賽車車架靈敏度分析與輕量化設計[J].廈門理工學院學報, 2015: 7-12.