資本資產定價模型及應用
韓寶燕
1 資本資產定價模型的基本假設
資本市場是一個極其復雜的市場,它包含的決策變量極多,任何一個決策變量發生變動,都會對整個市場造成重大的沖擊。因此,需要設定一些簡單的假設條件,以方便對資本市場的研究。
1.1 關于市場的假設
首先,資本市場是完全的,既沒有交易成本,也不存在稅負,這會降低模型的復雜度,便于分析。第二,資本市場是完全競爭的市場,市場價格由社會總供求行為決定,任何投資者都不能對市場造成太大的影響,這就要求市場上存在足夠多的投資者。第三,市場上存在無風險利率,所有的投資者都可以用相同的利率進行貸款。第四,資產是可分的,任何一部分,無論多少,都可以進行單獨買賣,這就避免出現資產不足無法買賣的現象。第五,所有的市場信息都是公開的,任意投資者都可以免費獲取,不存在信息上的摩擦,這就保證了市場的公平公正。
1.2 關于投資者的假設
首先,所有投資者都是風險厭惡型的,他們追求利益但是十分厭惡風險,風險的承受能力也比較弱。當他們面臨其他條件都相同的資產組合時,他們更傾向于風險較低的組合。第二,所有投資者的投資期限都相同,這一假設也就忽略了投資策略對投資期滿后的影響。第三,投資者是貪婪的,永不滿足。當面臨的兩個資產組合風險相同時,他們會選擇收益更高的組合。第四,相同資產的標準差、協方差和收益率都相同。
2 兩種風險與B eta系數
資本市場上的風險有系統性和非系統性之分。系統性風險是指市場中無法通過分散投資來消除的風險,也被稱做為市場風險,是由整個大的社會經濟環境所決定,如利率變動、金融危機、政局不穩、自然災害、爆發戰爭等,都會對系統性風險有大的影響。它無法預測,也不能避免。市場上所有的公司企業都會受它的影響,只不過影響的程度不同。非系統風險也被稱作特殊風險,是受內部的因素所影響的,如管理者的管理水平、投資者的投資能力、公司的經營程度等。
資本資產定價模型中的系數—β,又稱風險補償,根據資本資產的要求,Beta系數是用來衡量一資產系統風險的指針,是用來度量一個投資組合或者一種證券相對總體市場的波動性的一種用來評估風險的工具。從市場組合來看,可以將單項資產的系統風險看作是對市場組合變動的反映程度,用貝塔系數度量。表示的是相對于市場收益率變動、個別資產收益率同時發生變動的程度,是一個標準化的度量單項資產對市場組合方差貢獻的指標,用來反映系統性風險的,通過承擔系統性風險來獲得補償。
3 資本資產定價模型
3.1 模型推導
從證券市場線可以看出,當σNM=0時,風險證券的收益率就等于無風險利率,即E(rN)=Rf.因此該證券與無風險證券一樣,不會對市場組合M的風險產生任何作用。當σNM<0時,該證券的預期收益率E(rN)甚至要低于Rf。又因為證券N的β系數為,把它代入證券市場線的公式中,可以得到:E(rN)=Rf+[E(rM)-Rf]βN.
上式便是標準的資本資產定價模型,英文簡稱CAPM。
該式表明,單個證券N的預期收益率由兩部分構成,一是無風險的收益Rf,二是風險收益[E(rM)-Rf]βN。在[E(rM)-Rf]βN中,[E(rM)-Rf]是組合M的風險報酬,βN是證券N相對于組合M的風險的大小,因此,[E(rM)-Rf]βN也被認為是N的風險報酬。由此也可以看出資本資產定價模型遵循著高風險高收益的原則。
3.2 β系數
β系數反映的是證券與市場組合之間風險的大小。從CAPM模型中可以得到:
當βN>1時,E(rN)>E(rM),這表示該證券的收益率和風險程度都高于市場平均水平。當βN=1時,E(rN)=E(rM),該證券與市場組合完全正相關,收益率和風險程度相同。當βN<1時,E(rN)<E(rM),這表示該證券的收益率和風險程度都低于市場平均水平。當βN=0時,E(rN)=Rf,該證券是無風險證券。
4 資本資產定價模型的適用范圍
證券市場線與資本市場線是CAPM模型中的兩個重要的結論。其中,證券市場線反映的是單個證券的E(rT)與市場風險間的關系,而資本市場線反映了有效組合的E(rM)與系統性風險的關系。所以CAPM模型既適用于單個證券的情況,也適用于任意證券組合的情況。這是因為,任意證券組合的收益率都等于組合里各個證券的加權平均收益率,任意β系數也等于各種證券β系數的加權平均數,權數是其組合比例。
設各證券在組合中所占的比例為W1,W2,…,Wn,則有:
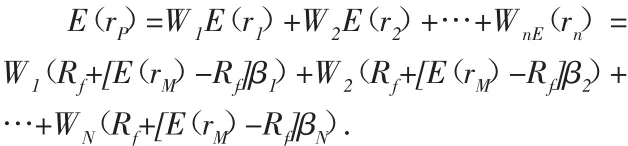
令βP=W1β1+W2β2+…+WNβN,代入上式,得
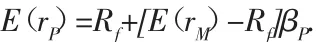
可見,無論是單一證券還是證券組合,都可以用CAPM模型來描述,那些由證券構成的任意證券組合都可以用資本資產定價模型來預期其收益率與風險程度的關系。
參考文獻:
[1]哈里·馬科維茲.資產組合選擇和資本市場的均值- 方差分析[M].上海:人民出版社,2006:65-72.
[2]約翰·赫爾.期權、期貨及其他衍生品[M].北京:清華大學出版社,2011:451-470.

