基于Ordinal Logistic模型的事故嚴重性影響因素分析
——以翻車事故為例

胡　驥，閆章存，盧小釗，王　鵬，張敏捷，胡萬欣

(1.西南交通大學 交通運輸與物流學院，四川 成都 610031; 2.建筑與交通工程學院 寧波工程學院，浙江 寧波 315211； 3.武漢鐵路職業技術學院，湖北 武漢 430205)

0　引　言

隨著我國社會經濟的發展，生活質量的改善，人們對小汽車的依賴度越來越高，交通事故卻頻頻發生。近年事故總量雖有所下降，但因事故所造成的損失仍居高不下。為了有效預防交通事故減少人員傷亡和財產損失，需要準確的把握事故原因，從而因地制宜做好事故預防措施。因此，有必要對影響事故嚴重性的因素進行科學的分析。

由于交通事故是在交通活動中由人、車、路、環境等因素相互耦合失調導致的不幸事件，事故類型千變萬化，原因錯綜復雜，很難用一個固定的模式或者方程來精確解釋，目前較為常用的是基于計量經濟學模型、統計分析模型、事故樹法、因果分析法等分析手段。例如，F. H. AMUNDSEN等[1]對挪威公路隧道交通事故進行研究，利用因果分析法分析隧道長度、天氣、交通量以及公路條件等因素對事故嚴重性、事故發生位置的影響關系；M. W. KNUIMAN等[2]研究美國伊利諾斯州和猶他州道路中央隔離線與碰撞率之間的關系，并發現當中央隔離線較寬時車輛正面碰撞、刮擦以及單車事故率都會下降；J. K. KIM等[3]依據事故死亡人數將交通事故嚴重程度分為4個級別，建立預測事故態勢的多項Logistic模型；C. LEE等[4]依據事故死亡人數將交通事故嚴重程度分為5個級別，建立了分析影響嚴重程度要素的有序響應模型。國內這方面的研究相對較少，宗芳等[5]應用Ordered Probit模型分析受傷人數的影響因素，計算各影響因素的邊際貢獻，并進行了受傷人數的預測；馬壯林等[6]對京珠高速公路韶關段4個隧道的交通事故數據，利用Logistic模型分析事故發生時段、碰撞類型、天氣等因素對事故嚴重性的影響，經檢驗表明Logistic模型在事故嚴重性影響因素分析中具有較好的適應性和實用性；李世民等[7]調查北京周邊無信號三路交叉口交通事故數據，并建立Logistic模型分析，得出交叉口轉彎車輛比例、控制方式和土地開發強度對無信號三路交叉口交通事故的嚴重性有顯著影響。

1　模型選擇

一般認為交通事故的嚴重程度存在順序的內涵特性，且嚴重程度與事故變量之間關系是非線性的，簡單的使用多項式Logit模型并不能準確的分析交通嚴重程度的影響因素。對于存在一定次序的變量分析通常選用Ordinal Logistic和Ordinal Probit模型，它們是基于連續的、分類的變量的分析模型，且可以利用相關因素來預測可能性的模型。筆者選用Ordinal Logistic模型，建立翻車事故嚴重性順序值的回歸模型，分析各個因素對事故嚴重性影響的程度，力圖提高影響翻車事故嚴重程度的因素分析的準確度。

2　建立模型

2.1　Ordinal Logistic 模型

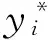
(1)

式中：τ={γ0，γ1，…，γj，…，γJ}表示被解釋變量(嚴重程度)分界點的向量，且(γ0<γ1…<γj…<γJ，γ0=-∞，γJ=+∞)。

模型中被解釋變量(因變量)的觀測值y表示排序結果或分類的結果，解釋變量(自變量)X是影響解釋變量排序的各種因素，也可以是多個解釋變量的集合。Ordinal Logistic模型的一般形式為

(2)

B={β0，β1，…，βk，…，βK}

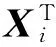
Logistic模型中假設εi的概率密度函數為f(εi)，累積分布函數為F(εi)，Eεi=0由式(1)和式(2)可得到第i個觀測對象的嚴重性為j的概率為

(3)

當εi有一個標準的邏輯分布[i.e.，f(εi)=eεi/(1+eεi)2，F(εi)=eεi/(1+eεi),Var(εi)=π2/3] 時，嚴重性“j(或者更低)”相對于“高于j”概率的比值可以表示為

(4)

從式(4)可以看出某一具體變量Xk改變一個單位對嚴重程度所產生的數量化影響，可以通過概率比exp(-βk)來表示。

2.2　參數估計

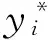
(5)

這里是指標函數δyi=jXi，B，Γ等于0或1，通過式(5)的最大化給參數估計值：

3　模型解釋變量篩選方法

常用篩選變量的方法包括向后刪除變量法、向前刪除變量法和逐步回歸法3種，這3種方法在估計標準誤差和通過判定P值是否合理來刪除臨界變量方面有優越性，更為重要的是在分析的過程中不用考慮變量的獨立性。一般要求選入變量的顯著性檢驗水平αs小于或等于變量刪除的顯著性水平αe，實際應用中常取αs=αe，αe常取值0.05。

相比這3種方法而言，K. P. BURNHAM等[8]提出一個更好的方法：通過使用統計學方法比較由相同數據所建立的不同模型的結果、合理性、擬合優度來進行模型擬合優良性的衡量標準。常用的統計參數有赤池信息準則[9]AIC(the Akaike information criterion)和貝葉斯信息準則BIC(Bayesian information criterion)。AIC指標在對數似然值的基礎上，考慮統計模型中的解釋變量個數。AIC的定義式為

AIC=2K-2lnL

(6)

式中：K為模型需要估計的總體參數(包括截距項和解釋變量)個數；L為極大似然值。

由于K越小模型約簡潔，而且對數似然值越大模型約精確，因此模型的AIC越小越好。

BIC指標也是建立在對數似然值的基礎之上，且與AIC指標密切相關，同時BIC對自由變量的懲罰效果更加明顯。BIC的定義式為

BIC=AIC+K·(lnN-2)

(7)

式中：N為樣本大小；其他參數同上。

BIC信息準則對解釋模型有較好的簡約性，即當其他參數相等時，對于兩個似然估計值相等的模型，BIC較小的模型被認為是更好的。

然而，在自由變量數量相對樣本的規模較多時，信息準則的懲罰效果不是很好。對這一問題N. SUGIURA[10]提出了一個被廣泛應用于小樣本的精確指標AICC，其表達式為

(8)

式中：參數同上。

因此模型中的AIC值、BIC值及AICC值越小表示模型越接近真實模型。

4　回歸模型評價與參數檢驗

對于所建立模型優劣的評估，需要對模型進行平行線假設的檢驗和似然比檢驗。

1) Ordinal Logistic模型平行線假設檢驗[11-13]：在累積概率的j-1個有序多分類的Logistic模型中僅有臨界點γj變化外，而回歸系數保持不變，稱之為平行線假設。同時不同等級的解釋變量的效應始終一致，不會隨著等級的改變而不同，因此平行線假設又稱比例優勢假設(proportional odds assumption)。例如一個4分類有序結果變量可以表示成如下的3個方程[11]：

(9)

假設只有一個解釋變量的情形，圖1表示其概率曲線。

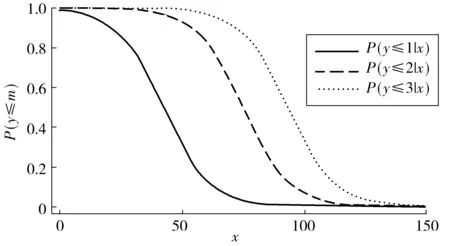
圖1　累積概率曲線Fig. 1　Cumulative probability curve

由于平行線假設3個方程回歸系數保持不變，因此圖1中的3條曲線形狀相同，僅僅因為臨界點yi的不同而導致了曲線向右或向左平行移動。

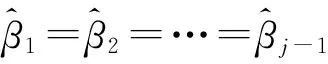
2) Ordinal Logistic模型似然比檢驗[15]。對事故的嚴重程度分類后，需要對Ordinal Logistic回歸模型的“比例性”假設條件進行檢驗，通過該假設條件檢驗建立模型的擬合是否可靠。

Ordinal Logistic模型“比例性”假設條件需通過構造統計量G并采取χ2檢驗計算公式為

G=-2(lnLP1-lnLP2)

(10)

式中：LP1為模型P1的對數似然值；LP2為模型P2的對數似然值，模型P1和模型P2是所得到的不同嚴重程度的Ordinal Logistic回歸模型。

通常顯著性水平低于0.05，說明χ2值統計性不夠顯著，表明Ordinal Logistic回歸模型是適用的，符合“比例性”的要求。

5　案例分析

5.1　變量說明

考慮到數據獲取的方便與質量，筆者選用美國HSIS(Highway Safety Information System)中北卡羅萊納州2010—2014年的交通事故數據，選擇鄉鎮兩車道公路上的翻車事故數據作為研究對象。參考相關翻車事故分析的文獻結合實際經驗選擇出13個變量作為討論變量，其中包括駕駛員、道路、環境3個類型的變量，具體如表1。根據所需變量的特征在數據庫中進行數據整合與篩選，最終選擇出385個滿足要求的完整事故樣本。

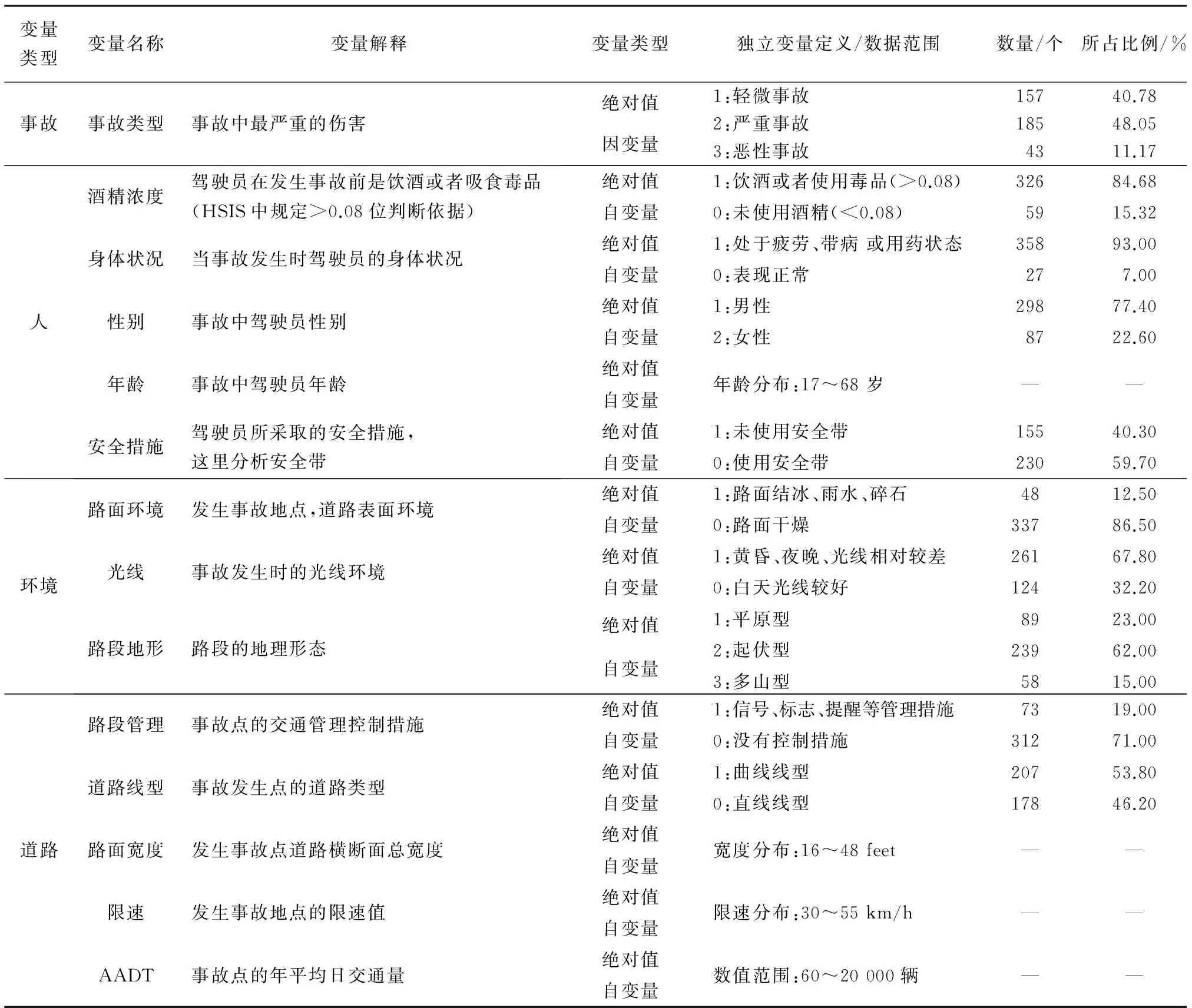
表1　翻車事故嚴重程度的影響因素和變量設置Table 1　Influence factors of rollover accident severity and variables setting

5.2　模型的建立與檢驗分析

利用SAS軟件進行Ordinal Logistic回歸處理，并得到相關的估計參數和檢驗系數，采用向后刪除變量法剔除影響相對較小的變量，逐步處理并得到最后的結果，如表2。

模型A-1包含是否使用安全帶這一變量的p值小于0.000 1，并且在后面的6個模型中一致，可以判斷駕駛員是否系安全帶這一因素對翻車事故的嚴重性具有重大影響。然而在該模型中駕駛員的身體狀況變量的p值(0.616 2)和變量駕駛員性別的p值(0.573 1)相對較大，且現實中兩者對交通事故的嚴重程度的影響也相對較小，因此在模型A-2中將其排除。在模型A-3中駕駛員酒精濃度、駕駛員年齡、安全帶、路面狀況、光照條件、道路線形、地形、限速等8個變量的置信度在90%的水平，只有AADT、路面寬度兩個變量的p值大于0.1。經過進一步的變量排除過程可以得到所有變量置信度均大于90%的模型A-4。且模型A-1到模型A-4，AIC、BIC和AICC值也在降低，這說明模型的簡約性在不斷地提高。

在模型A-5中的由于地形變量和道路線形變量具有一定的相關性，因此分別選擇其中一個進入最終的模型。對比結果發現變量“地形”進入模型時，模型AIC值為690.838、BIC值為710.604，均大于變量“道路線形”進入模型分析所得的結果，并且所得模型中所有變量的置信度均在95%水平。同時模型評估參數BIC值也在減小，因此確定A-6為最終模型。A-6的表達式如下：

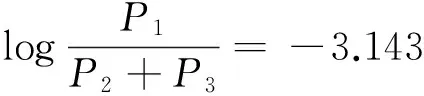
(11)

(12)

式中：P1表示輕微事故，P2表示嚴重事故，P3表示惡性事故；x1表示安全措施，這里主要分析事故發生時是否系安全帶(系安全帶其值為0，未系安全帶其值為1)；x2表示發生事故時的道路路面狀況(路面干燥其值為0，路面有結冰、雨水、碎石其值為1)；x3表示事故地點的道路線形(直線線形其值為0，曲線線形其值為1)。

解方程得發生預測概率為

(13)

(14)

(15)

P1+P2+P3=1

(16)

對模型A-5的平行線假設進行得分檢驗得(p=0.115 1，df=3)，驗證了原假設累積Ordinal Logistic是平行的。由此可得：模型A-5非常適合這一數據；同時似然比檢驗得(p<0.0001，df=3)，顯著性水平為0.000 1，遠低于0.05水平，統計性顯著，原假設目標是被拒絕的，說明模型A-5中的變量對翻車事故嚴重程度具有實質性的影響。

根據顯著變量估計效應檢驗所得的結果可以看出，使用安全帶和不使用安全帶的比值比為exp(1.520 6)=4.575，這一結果說明相同的環境下駕駛員不使用安全帶的事故嚴重程度比使用安全帶的事故嚴重程度將會增加357.5%，即表明在翻車事故發生時不使用安全帶將會造成非常嚴重的后果。同理分析可得：發生翻車事故時，良好的路面環境對事故的嚴重程度，相比惡劣的路面環境所產生的影響較少55%；不良道路線形對翻車事故的嚴重程度比良好的道路線形對翻車事故的嚴重程度的影響相比增加76.4%。

6　結　論

通過以上研究，形成以下主要結論：

1) 采用Ordinal Logistic模型對翻車事故的嚴重程度進行分析，以事故的嚴重程度作為因變量，選取駕駛員特性、道路特性、環境特性3個方面的13個因素作為自變量。研究過程中采用美國一州的交通事故，篩選出385個滿足條件的樣本數據，建立了影響翻車事故嚴重程度要素分析的邏輯模型。

2) 利用最大似然估計法對模型參數進行估計；運用AIC、BIC、AICC以及對數似然估計進行模型變量的精簡；同時運用比例優勢假設和似然比檢驗以及比值比效應檢驗的方法對模型做了檢驗，得到符合檢驗假設條件的最優模型。該模型中包含3個顯著變量，且置信度水平為95%。

3) 通過筆者分析確定影響翻車事故嚴重程度的主要因素為安全帶的使用、路面狀況及道路線形，且3者中變量“安全帶”在模型簡化的過程中其p值一直小于0.000 1。其對翻車事故嚴重程度具有最為明顯的影響，很好的印證了安全帶的重要性。

總體而言，筆者提出的翻車事故分析模型能夠較為準確的反映翻車事故嚴重程度，但對于模型中變量的獨立性尚未進行完整的檢驗。在將來有必要深入分析變量之間的獨立性檢驗，進一步完善模型。

參考文獻(References)：

[1]AMUNDSEN F H，RANES G.Studies on traffic accidents in Norwegian road tunnel[J].TunnellingandUndergroundSpaceTechnology，2000，15(1)：3-11.

[2]KNUIMAN M W，COUNCIL F M，REINFURT D W.AssociationofMedianWidthandHighwayAccidentRates[R].Washington，D. C.：Transportation Research Record，1993.

[3]KIM J K，KIM S，ULFARSSON G F，et al.Bicyclist injury severities in bicycle motor vehicle accidents[J].AccidentAnalysis&Prevention，2007，39(2)：238- 251.

[4]LEE C，ABDEL-ATY M.Comprehensive analysis of vehicle pedestrian crashes at intersections in Florida[J].AccidentAnalysisandPrevention，2005，37(4)：775-786.

[5]宗芳，許洪國，張慧永.基于Ordered Probit模型的交通事故受傷人數預測[J].華南理工大學學報(自然科學版)，2012，40(7)：41-45.

ZONG Fang，XU Hongguo，ZHANG Huiyong.Forecast injury number due to traffic accident based on Ordered Probit model[J].SouthChinaUniversityofTechnology(NaturalScienceEdition)，2012，40(7)：41-45.

[6]馬壯林，邵春福，李霞.基于Logistic模型的公路隧道交通事故嚴重程度的影響因素[J].吉林大學學報(工學版)，2010，40(2)：423-426.

MA Zhuanglin，SHAO Chunfu，LI Xia.Analysis of factors affecting accident severity in highway tunnelsbased on logistic model[J].JournalofJilinUniversity(EngineeringandTechnologyEdition)，2010，40(2)：423-426.

[7]李世民，孫明玲，關宏志.基于累積Logistic模型的交通事故嚴重程度預測模型[J].交通標準化，2009(3)：168-171.

LI Shimin，SUN Mingling，GUAN Hongzhi.Prediction model cumulative logistic for severity of road traffic accident[J].TransportStandardization，2009(3)：168-171.

[8]BURNHAM K P，ANDERSON D R.ModelSelectionandMultimodelInference[M].New York：Springer，2002.

[9]AKAIKE H.Information theory and an extension of the maximum likehood principle[J].InternationalSymposiumonInformationTheory，1973，1：610-624.

[10]SUGIURA N.Further analysis of the data by Akaike’s information criterion of model fitting[J].CommunicationinStatistics-TheoryandMethods，1978，7(1)：13-26.

[11]趙晉芳，范月玲，曾平，等.多分類有序logit模型資料平行線假設及檢驗方法[J].中國衛生統計，2009，26(1)：11-13.

ZHAO Jinfang，FAN Yueling，ZENG Ping，et al.The parallel line assumption of ordinal logit regression model and its test the department of health statistics[J].ChineseHealthStatistics，2009，26(1)：11-13.

[12]REES H.RegressionModelsforCategoricalandLimitedDependentVariables[M].3rd ed.Texas：StataCorp LP，2014.

[13]MCCULLAGH P.Regression models for ordinal data[J].JournaloftheRoyalStatisticalSociety，1980，42(2)：109-142.

[14] WOLFE R，COULD W.AnApproximateLikelihood-RatioTestforOrdinalResponseModels[M].Texas：StataCorp LP，1998.

[15] 劉夢涵，于雷，張雪蓮，等.基于累積Logistic 回歸道路交通擁堵強度評價模型[J].北京交通大學學報，2008，32(6)：52-56.

LIU Menghan，YU Lei，ZHANG Xuelian，et al.Cumulative logistic regression-based measurement models of road traffic congestion intensity[J].JournalofBeijingJiaotongUniversity，2008，32(6)：52-56.