交通事件下排隊車輛數和總延誤計算模型研究

董國華 左友蘭

摘要：為描述交通事件后導致擁擠交通流中的排隊現象，分析預測交通流的時空影響。根據流量守恒定律和交通波波速公式，提出了排隊車輛數和車輛總延誤定量計算的一個新模型。將事件后交通流的發展劃分為三個時間階段，推導出道路堵塞時各相應時間段交通變量動態計算公式。同時分析了交通事件影響因素除了事件本身的嚴重性外，事件的清理時間是決定事件瓶頸處車輛排隊第二位的影響因素;以及交通事件時空發展模型與事件自動檢測兩者之間相互影響、互為因果的關系。最后用應用算例對該模型的有效性進行驗證，結果表明，數據符合實際情況，排隊車輛數隨著事件持續時間增加呈分段線性變化，而所有排隊車輛的總延誤隨著交通事件處理時間的增加呈二次平方變化。此模型可作為交通管理控制部門對交通事件發生后制定合理救援措施的理論依據。

關鍵詞：交通事件;影響因素;交通流;排隊車輛數;總延誤;模型分析

中圖分類號：TP399

文獻標識碼：A

1 引言

近年來，由于我國機動車越來越多，人、車、路等矛盾也越來越突出。在高速道路上，交通事故、車輛故障、貨物散落、大貨車占道、修路養路、路邊停車、流量激增等交通事件是造成偶發性交通擁堵的主要原因，尤其是在節假日，事件發生后導致車輛排隊現象在交通運輸系統中隨處可見。交通事件發生后，原交通流的車流量會發生改變，車流量的波動甚至會傳播到其它相鄰的道路上去。因此，交通事件對交通流的定量影響一直是一個倍受各方關注的問題。特別是事件發生后，排隊車輛數和總延誤隨時間如何增長，與事件特性如交通流量、車道數、事件處理效率等有何關系，對交通流預測、事件預警以及交通管理和控制都有重大意義[1]。

國內外很多研究者一直致力于排隊現象的分析和交通流參數預測。上世紀70年代，日本Akaike提出的Akaike信息準則（Akaike Information Crite-na，AIO經過各國大量實踐證明，對交通流的預測精度在70%-800/0。阿里巴巴的Wanli Min[2]采用半鞅理論、網絡交通模型、基于高德地圖實時數據和歷史數據對交通流預測準確率穩定在91010以上。Guo Huan[3]等人研究成果為基于灰色模型的短時交通流預測方法，充分考量了交通流的非線性以及延遲特征。Hani S.Mahmassani[4]等人研究探討了在大規模復雜城市嚴重堵塞街道網中交通流極限關系性能，包括“死鎖”的形成、傳播、恢復、大小等。此擁堵現象的特點暫時很少人關注，是比較新穎的一個問題。Treiber M.、Kesting A[5]提出了一個新的跟車理論動力學模型，微觀與宏觀變量相結合，該模型可以很好地模擬交通流擁堵、擁堵疏散、走走停停現象和幽靈幻象等狀況。王殿海[6]等人針對雙向兩車道路內停車路段，分流量較大和較小兩種情況建立了相應的延誤影響模型，并利用VISSIM仿真軟件模擬數據對模型進行了驗證。張晶晶[7]用交通波理論研究交通事故直接影響范圍，用節點聯系強度建立事故上游車輛繞行計算模型來研究間接影響范圍。曹志遠[8]等人基于交通事故下采取限、分流措施分析了交通波的影響，得到了交通流演變過程中的擴展時區、穩定時區、啟動時區，三個時區的時空影響范圍。胡繼啟等[9]利用海量收費數據有效計算出相鄰兩個收費站之間路段上的擁堵初發點位置和初發時刻，此文研究屬于事件檢測范疇，與本文交通事件時空發展模型相互影響、互為因果的關系。

綜上所述，道路發生交通事件導致擁堵后，很多學者只是定性分析交通變量，而事件具體的發展過程如何，與事件特性、事件處理效率等因素有何關系，相關受影響的變量隨時間變化的定量規律等很少有研究者關注，目前極其缺少此類問題的解決方案。因此，本文以道路公路基本路段（一條道路）和收費站匝道與一條主干道（兩條道路）發生交通事件為例，分析事件具體的發展過程與影響，以及交通事件發生后不同時間段內事件點各交通變量動態計算模型，分析事件發生與事件檢測兩者之間有何關系，用于以后進一步的突發事件下交通流預測工作。

2 交通事件影響的三個時間階段分析

由于交通事件的發生時間和發生地點是隨機的、不可預測的，因此很難采取控制交通需求或提高道路通行能力等對策來處理，解決問題的重點在于及時發現事件，準確評估事件性質，迅速實施應對措施，并立即向其他司機通告事件情況，從而對事件實現快速、高效、恰當的處理[10]。

交通事件發生后，對于較小的事件，如只是輕微的刮擦，在不對交通運行造成影響的前提下可不進行處理，節約人力物力，以免在處理的過程中由于救援車輛的占道使事件影響更嚴重或增加車輛排隊和延誤。而對于較嚴重的交通事件可進行快速理賠的原則，確定責任后雙方快速撤離現場，節約事件的清理時間，減小排隊車輛數和車輛延誤。而對于嚴重的交通事件可進行報案由交通管理部門處理，不過它可能需要耗費很長的處置時間，自報案到交警抵達事件現場，再到完成問題處理、恢復道路交通，不僅耽誤雙方時間，還會加大事件的影響力，增加車輛排隊和延誤。所以發生交通事件后，需要實施適當的救援措施，倘若方法不正確，很可能造成二次事件，加重交通擁堵狀況。而倘若方法過當，那么極有可能產生交通資源浪費。通過以上分析可知，除了事件本身的嚴重性外，事件的清理時間也影響著車輛排隊。

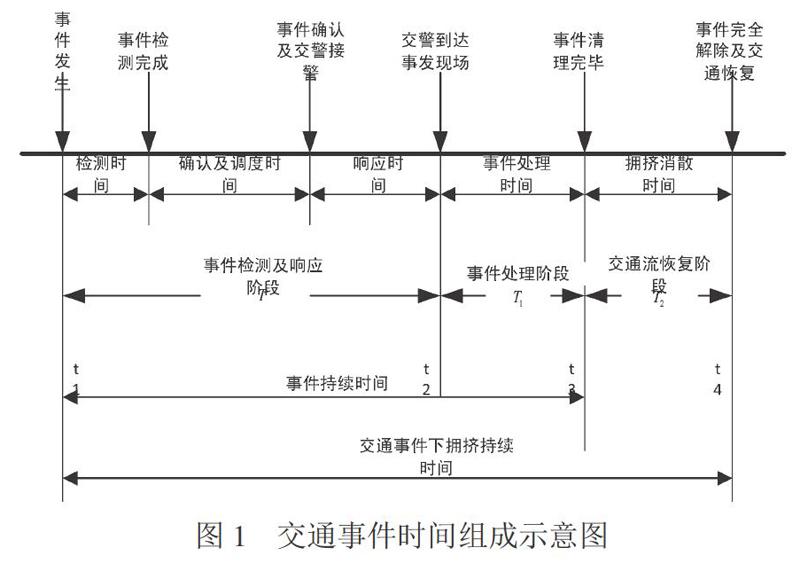
交通事件后，因為自發生交通事件開始，歷經事件檢測、核實情況、交警處置、清理結束、恢復交通、消除排隊等環節，都要耗費相應時間。因而可將整個事件分為3個時間階段：第一階段時間指從事件產生至交警抵達現場進行時間處理這個期間，事件確認接警時間以T表示。第二階段時間指從開始處理事件至交通開始恢復這一期間，對應的事件處理時間以T1表示。第三階段時間指自現場交通恢復開始，直至事件上游車輛排隊不繼續增加，再到最后完全消散[11]，對應的排隊消散時間以T2表示。交通事件時間組成示意圖如圖1所示。

在T時間內，事件現場維持不變，尚未開始處理，此時可分成兩中類型進行分析：（1）交通事件占據部分車道，事件位置的剩余通行能力Qs≠0，若交通事件愈重，那么Qs愈小。當上游的交通需求QQs，那么事件點的交通流與剩余斷面通行能力對應，在上游會出現排隊現象。（2）如果交通事件特別重大，以至事發位置的剩余通行能力Qs=0，則形成斷流現象，車輛無法通過該路段，只能在上游排隊，擁堵現象加劇，且排隊沿著上游方向延續[12]。

T1時段里，當完成交通事件確認后，管理部門抵達現場開始處理，這期間事件點交通仍受持續影響，事件斷面通行能力同步發生改變[13]通常會減小，甚至完全封閉。當擁擠嚴重時，則車輛排隊加劇。在T和T1兩個階段，事件位置上游可能出現排隊;如果無車輛排隊，那么T2=0;如果存在車輛排隊，那么要等到事件處置完成和道路交通恢復后，車輛排隊狀態才能逐步消除，那么T2≠0。T2可理解為交通事件的持續影響時間，具體指事故處理完成、道路恢復通行到車輛排隊不繼續增加這個期間，也能看成是消散波自隊列首部傳遞到尾部所耗費的時間[14]。

由以上分析可知，交通事件發生的嚴重性、事件后所占用的車道數、上游交通需求以及事件清理時間等都是影響事件瓶頸處車輛排隊的重要因素。而事件嚴不嚴重是事件發生時由事件本身決定的，事件后人為無法改變;而事件后所占用的車道數是由道路的物理結構和事件本身決定;而上游交通需求是由道路所在的位置和時間決定，若是處于交通運行的關鍵路段或節假日交通需求量大的時間段，則上游交通需求量增大，反之，上游交通需求量減小;而事件清理時間是人為決定的，是后續可控的事件影響因素。事件處理效率越高或清理時間越短，排隊車輛數越少，則排隊消散快些;事件處理效率越低或清理時間越久，導致排隊車輛數越多，排隊消散的時間也越慢。因此，交通事件眾多影響因素中除了事件本身的嚴重性外，可控因素中只有事件的清理時間是最重要的。即事件的清理時間是事件瓶頸處決定車輛排隊第二位的影響因素。

3 分時間段建立模型

根據上一部分分析可知，交通事件發生后事件演化的三個時間段中前兩部分時間構成車輛排隊形成階段，到事件處理完畢恢復道路交通時，排隊車輛數達到最大值，排隊開始消散，即第三部分時間構成排隊消散階段。本文假設在事件處理過程中有車輛排隊，即第二節中的第（1）種Q>Qs情況，則交通流可按事件點的剩余斷面通行能力通過事件點，超過該通行能力的車流在事件點上游排隊。由常規可知，排隊車輛數和排隊長度隨時間線性增長，越晚加入排隊，越晚離開，總延誤等于所有排隊車輛延誤之和。

3.1 排隊車輛數計算模型

通過以上分析，假設如圖2所示發生交通事件的基本路段為單向三車道，設道路正常情況下通行能力為Q'，在同級服務水平上，在α點發生交通事件后占用最右側車道，而且事件處理過程中也只占用最右側車道（即事件處理過程中事件點交通沒有受到進一步影響），則道路通行能力會下降，變為剩余通行能力Qs。根據第二節分析，可設t=0時發生交通事件，即車輛開始排隊，則每分鐘內就有Q'-Qs輛車加入排隊，t=T1時刻障礙清理完畢，下游開始疏散，疏散速度Q'> Qs，完全疏散時刻就是t=T2，根據車輛守恒定律，則有：

由于事件發生后從事件檢測到事件接警處理過程中以及到事件處理完畢，這部分過程都假設交通流沒有受進一步影響。而根據現實情況，在事件處理過程中，交通管理指揮者也會盡可能使交通流的影響降到最低。所以根據時間分段，可將事件檢測響應階段T與事件處理階段T1合并。交通事件清理完畢后，道路交通恢復正常。事件下游開始消散，但由于消散波傳到隊尾時還需一定的時間，所以事件上游在完全消散前還在慢慢排隊。則排隊車輛數隨時間的變化有：

3.3 延誤時間動態計算模型

從3.1節可知，延誤是理想行程時間和實際行程時間之差。由于沒有實際的交通事件時空發展數據，本文由交通事件發展的三個時間段直接計算車輛延誤，從事件發生到事件處理完畢，就是車輛的等待時間。但由于每輛車到達和離開的時間都是變化的，這里引入排隊消散動態時間函數τ（t），根據每輛車到達和離開的時間不同，分別計算每輛車相應的延誤，即每輛車排隊等候的時間加上排隊消散的時間就是每輛車所耽誤的時間。通過計算出每輛車的延誤，再把斷面所有車輛延誤之和即為總延誤。

從計算公式中可知，排隊車輛數隨著排隊形成時間和排隊消散時間都是一個線性變化的關系。隨著事件的發展，排隊的車輛越來越多，排隊車輛數隨著交通事件持續時間增加呈分段線性變化。而排隊車輛的總延誤隨著交通事件處理時間的增加呈二次平方變化。

3.4 交通參數計算步驟及算法實現

1）交通參數計算步驟

交通事件下對交通流的預測研究就是對交通流參數的預測研究。而本文中建立的模型，其實就是對交通流參數的計算預測。而基于湖南省道路交通的實際情況，湖南省交通廳的數據中心還在建設之中，目前還無法獲取數據進行精確的實驗，只能根據本文的實際情況，用簡化假設的方法，擬確定如下方案得以實現。

首先簡化交通事件實例，根據具體實例，如圖2所示假設己知量，此模型中假設正常情況下，并在道路的同級服務水平條件下，假設在事件處理過程中交通流沒有受到進一步的影響，則己知的量有：道路正常通行能力Q'、剩余通行能力Qs、事件清理完畢時刻T1、以及下游疏散速度Q'>Qs具體處理程序如下：

1）模型參數輸入：Q'、Qs、T1;

2）根據流量守恒定律，得出T1和T2的關系;

3）根據時間分段，建立排隊車輛數隨時間變化的分段函數n（t）;

4）以事件發生的起始位置為位置坐標原點，左邊為負軸（事發地點上游），右邊為正軸（事發地點下游），建立位置坐標軸x;以事件發生的起始時刻為時間坐標原點，右邊為正軸建立時間坐標t;

5）根據流量密度的定義，分時間段建立下游前沿位置函數關系x_doun（t）;

6）根據格林伯速度一密度模型結合交通波波速公式，得出排隊車流速度Qs/ρ_max

7）引入時間函數τ（t），記為消散波傳輸的時間。結合步驟五，再根據集結波與消散波傳播的位置相等，得出消散波傳輸時間τ（t）函數;

8）求所有車輛的總延誤D，即是對每一輛車的延誤之和，利用積分法求出D;

9）模型參數輸出：T2、n（t）、D。

根據以上步驟即是本文算法的實現。

2）算法實現

本文提出的交通事件后交通流參數計算算法

偽代碼如下所示：

算法1.基于交通事件下排隊參數計算算法

輸入：Q'、Qs、T1

橫坐標軸位置：x;縱坐標軸時間：t

最大密度：ρ_max

阻塞密度： ρf

輸出：T2、n（t）、D

4 模型分析

通過概括國內外學者的研究，交通流參數估計的模型有很多，如葛興、王殿海等人的路內停車模型;經典紅綠燈模型;姚榮涵、王殿海的擁擠交通流當量排隊長度變化率模型等等。接下來主要分析經典紅綠燈模型與本文提出的交通事件時空發展模型。

4.1 交通事件時空發展模型

道路發生交通事件后，人們通常關心事件發生的時間、地點，而很少有人關注事件的演化過程。事件發生持續多長時間，5 min、10 min后事件發生情況、嚴不嚴重。事件導致擁堵產生排隊后，是否還能通行，車輛排隊是否占據整條道，還是己蔓延到相鄰路段上，如蔓延鄰路段上，是否導致相鄰路段也擁堵產生排隊，進而波及相鄰的一條道或幾條道，導致整個路網產生擁堵，甚至“死鎖”現象的發生。

根據謝立新[14]在2016年湖南省高速公路工作會議工作報告中的數據顯示，到2015年底全省高速公路通車里程達到5653公里，這么多公里數分成多條高速公路并且有的相互互通，毋庸置疑收費站也不少。而高速道路收費站擁堵導致排隊現象常有發生，節假日擁堵嚴重的時候在收費站排隊花費5、6個小時是人們通常遇到的問題，那么如何快速準確地對擁堵情況、事件演變信息進行定位，及時發布相應的道路運行狀態信息，是交通管理者和出行者最關心的問題。如圖5所示為一個高速公路出口匝道。當人們在收費站口等候出行時，由于車輛過多產生排隊，甚至一直排到匝道上去了，如果人工收費使車輛放行速度比車輛到達速度慢，排隊將一直增加，可能蔓延到主干道，繼而導致主干道也擁堵排隊，繼而發生交通事件。因而從一條道路發生交通事件，對事件進行檢測以及對交通流參數進行評估分析，到波及相鄰路段發生交通事件、對事件影響的交通變量又進一步進行分析預測。而事件檢測的數據結果可以作為交通流參數估計的數據輸入，進而對交通流進行預測;而對交通流預測的數據結果反過來又可以作為交通狀態判別的數據輸入。其實這就是從事件發生到事件檢測再到對事件影響下交通流參數進行評估預測的一個閉環，這兩者的研究結果相互影響、可相互作為各自模型的參數輸入，即交通狀態判別與交通量計算兩個模塊是相互耦合、串聯的關系。

4.2 經典紅綠燈模型

紅綠燈模型中假設道路交通在開始時處于穩定狀態，車流密度是常數，某個時刻路口的交通燈紅燈突然亮了，于是交通燈前面的車輛繼續行駛，而后面的車輛一輛一輛開始排隊擁堵起來。經過一段時間后，綠燈亮了，排隊的車輛開始消散。姜啟源[15]等人用交通流的模型描述了這個過程，并且綠燈亮后對堵塞車輛多長時間能追上遠離的車隊進行了計算，以及多長時間排隊能消散，使道路交通恢復正常。

由以上分析可知，（1）紅綠燈模型與本文模型相似，也可看作一次交通事件的發生和解除的模擬。紅燈開始時刻即為事件發生時刻，綠燈亮的時刻就是事件清理完畢、排隊開始消散時刻;而整個事件持續5分鐘后解除，即持續5分鐘的交通事件要75分鐘排隊才能消散。（2）紅綠燈模型中的紅燈時間τ越短，道路交通恢復時間t1越短，這說明事件的清理時間影響著車輛的排隊，與本文模型相一致，除了事件本身的嚴重性以外，事件的清理時間是決定排隊第二位的影響因素。（3）紅綠燈模型時間上具有周期性、地點也是固定的，而本文模型中交通事件發生的時間、地點都是隨機的。本文模型或事件現象更復雜、更難描述，因此更有研究的價值。（4）紅綠燈模型相當于道路封閉5分鐘，道路完全不能通行，而本文模型在道路發生交通事件后還有剩余通行能力，不是完全封閉狀態。紅綠燈模型就是本文模型中的一個特例，即本文模型中剩余通行為零的極限情況，在日常生活中除了紅綠燈之外是普遍存在的交通事件類型，適用性更廣，更有實際應用價值。

5 應用算例

如圖5所示，設某道路公路基本路段長度為500 m，單方向車道數為3，一個車道寬度為3.5 m。在道路上t=0時刻發生了一起交通事件，事件車輛占用一個車道6= 3.5 m，長度約為a=7m，事件點上游路段長度為300 m。假設道路正常情況下，單方向每分鐘100輛車通過，在同級服務水平上，若事件導致流量下降40%，單方向每分鐘只有60輛車通過，則單方向每分鐘有40輛車加入排隊，檢測延誤30秒的話，將影響到20輛車。

如圖2所示發生交通事件的道路基本路，根據公式（1），設t=0時車輛排隊開始，則有

分別設T1為5 min、30 min、60 min時刻，障礙清理完畢，根據公式（3）、公式（6）、公式（8），分別計算出排隊消散時間、最大排隊車輛數、總延誤如表1所示。

從表1中可以看出，此文模型計算出的各個交通變量結果比較接近實際情況。從車輛的總延誤時間來看，當T1=5 nun時，200輛車的車隊總延誤時間約為833 min，每輛車延誤約為4 min。把道路上的車輛都折算成小汽車的長度，包括車輛前后間距，每一輛車折算6米長，則200輛車的最大排隊長度約為1.2千米。當T1=30 min時，1200輛車的車隊總延誤時間約為30000 min，每輛車延誤約25 min，而1200輛車的最大排隊長度為7.2千米。此模型是在車流較大的情況下對數據擬合較好，要是高速道路嚴重堵塞、密度更大的情況下，如圖4.1所示的收費站匝道，車輛排隊7.2千米的話，匝道排隊肯定溢出。如若收費站放行速度比車輛到達速度慢，相當于交通需求Q> Qs，又或許道路的通行能力變得更小，后來的車輛繼續排隊，而一般匝道都是幾百米，所以排隊肯定排到主干道上去了，導致主干道也擁堵排隊甚至發生二次交通事件。則此情況屬于擁堵在交通路網上的傳播模式。

6 結束語

本文對道路交通事件影響下不同時間段內交通變量的動態變化進行了新的建模，較之經典紅綠燈模型更有實際應用價值。（1）本文通過分析得出，除了事件本身的嚴重性外，事件的清理時間是決定事件瓶頸處車輛排隊第二位的影響因素;（2）以高速公路出口匝道為例，用簡化假設的方法分析了交通事件時空發展模型與事件檢測兩者之間的數據結果可以作為各自模型的數據輸入，即兩者研究的數據結果相互耦合、影響、串聯的關系;（3）通過應用算例分析，在道路交通流量較小的情況下，排隊車輛數隨著交通事件持續時間增加呈分段線性變化，而所有排隊車輛的總延誤隨著交通事件處理時間的增加呈二次平方變化。流量較大或者剩余通行能力變小的情況下，道路車輛排隊溢出，使相鄰路段也受到影響。（4）下一步計劃是考慮動態瓶頸下交通事件影響模型、擁堵在公路網中的時空擴散，以及交通狀態判別與交通量計算兩個模塊具體的耦合。

參考文獻

[1]梅朵.基于云計算的交通瓶頸控制與誘導協同模型研究：[D].長春：吉林大學，2015.

[2]閔萬里，勞拉.溫特.實時道路交通預測與時空相關[J].交通研究C部分，2010，l9（2011）：8-11.

[3]郭歡，肖新平，福雷斯特.基于延遲的城市道路短期交通流量預測模型[J].交通運輸系統工程與信息技術學報，2013，l3（6）：60-66.

[4]MAHMASSANI H S，SABER M，ZOCKAIE A.城市網絡僵局：理論，特征和動態[J].運輸研究C部分：2013，36：480-497.

[5] TREIBER M，KESTINC A.動態交通流[M].紐約，斯德哥爾摩柏林海德堡，2013.

[6]王殿海，葛興，姜波.路內停車對交通流的延誤影響模型U].城市交通，2009，7（2）：1-5.

[7]張晶晶.路網環境下高速公路交通事故影響傳播分析：[D].西安：長安大學，2010.

[8]曹志遠，郭忠印，張起森，等.高速公路重大交通事故時空影響范圍研究[J].公路工程，2011，36（6）：56-58.

[9]胡繼啟，彭建，董國華，等.基于收費數據的交通擁堵出發點計算[J].計算機工程與應用，2015.15（1）：l-7.

[10]鄒力.物聯網與智能交通[M].北京：電子工業出版社，2012.

[11]陳誠，譚滿春.交通事故影響下事發路段交通流量變化分析[J].科學技術與工程.2011，11（28）1-2.

[12]張凡.典型交通事件下道路擁堵的網絡化蔓延特性研究[D].北京：北京交通大學，2014.

[13] WACENINGEN -KESSELS F.多類交通流模型：分析與仿真方法[D].荷蘭：荷蘭研究學院T-RAIL：代爾夫特理工大學，2013 年.

[14]謝立新.努力實現“十三五”高速公路發展精彩開局[A].2016年全省高速公路工作會議工作報告[C].長沙：湖南省高速公路管理局，2016：1-2.

[15]姜啟源.數學模型[M].北京：高等教育出版社，2011.