慣性串聯(lián)系統(tǒng)的自抗擾控制

李向陽　哀薇　田森平

實際應用中,被控對象的精確數(shù)學模型很難獲得,致使現(xiàn)代控制理論的許多控制算法很難在實際中取得良好的控制效果,實踐中大量應用的還是不依賴于精確數(shù)學模型的PID控制方法.我國著名學者韓京清研究員在吸取PID控制的基于誤差來消除誤差的優(yōu)點并克服其對信號利用率低的缺點的基礎上提出了著名的自抗擾控制(Active disturbance rejection control,ADRC)[1?2].經(jīng)過多年的發(fā)展,ADRC在理論研究和參數(shù)整定等方面取得了重要突破[3?21].ADRC對被控對象的模型信息依賴很少,只需要知道被控對象的相對階和控制增益的粗略估計,因此,在實際中應用越來越多.

在具體操作時,ADRC先把被控對象化為積分串聯(lián)系統(tǒng),然后應用擴張狀態(tài)觀測器(Extended state observer,ESO)估計出內(nèi)擾和外擾的總和,并加入控制量中實現(xiàn)補償控制,把非線性時變系統(tǒng)變成了線性系統(tǒng),最后對補償后的系統(tǒng)進行反饋控制,把閉環(huán)系統(tǒng)的極點配置到期望的位置.然而,對任何實際的系統(tǒng),都采用這種先把被控對象化為積分串聯(lián)系統(tǒng)的方法未必是最好的.例如,如果實際系統(tǒng)是慣性串聯(lián)系統(tǒng),強行把它化為積分串聯(lián)系統(tǒng)后系統(tǒng)的狀態(tài)將失去實際系統(tǒng)狀態(tài)原有的物理意義,是否可以保持慣性串聯(lián)以便與實際過程有很好的對應關系,而有利于實現(xiàn)控制系統(tǒng)故障診斷等其他功能,這要求ESO能直接估計慣性串聯(lián)系統(tǒng)的總擾動;另一方面,人們在長期系統(tǒng)操作過程中積累了豐富的系統(tǒng)模型知識,這些知識如何在ADRC中充分利用以便更好地提高控制性能,原有的積分串聯(lián)模型很難集成這些知識.

本文研究了慣性串聯(lián)系統(tǒng)的ESO和ADRC,以及慣性串聯(lián)系統(tǒng)ADRC與基于擾動觀測器(Disturbance observer,DOB)的控制之間的聯(lián)系.本文的結(jié)構(gòu)安排如下:第1節(jié)是對所研究問題的描述;第2節(jié)給出了慣性串聯(lián)系統(tǒng)的ADRC方法,及其與基于DOB控制的關系,給出了相關定理及其證明;第3節(jié)給出了仿真研究結(jié)果;第4節(jié)是本文的結(jié)論.

1　問題描述

考慮n階非線性系統(tǒng)

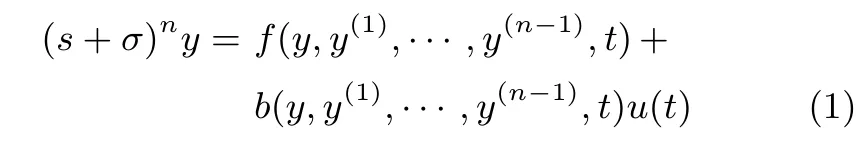
其中,s為微分算子,f和b為未知有界非線性時變函數(shù),u為系統(tǒng)的控制輸入,t為時間,n為系統(tǒng)階數(shù).系統(tǒng)(1)為慣性串聯(lián)系統(tǒng),并非是經(jīng)典ADRC[1?4]所要求的積分串聯(lián)型系統(tǒng),把式(1)轉(zhuǎn)換為

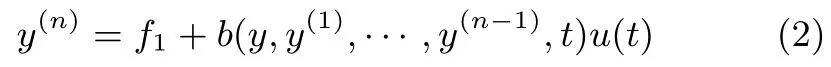
其中

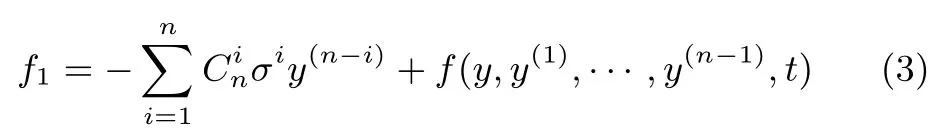
則系統(tǒng)(1)轉(zhuǎn)換為系統(tǒng)(2)的積分串聯(lián)型系統(tǒng),針對式(2),按照經(jīng)典的積分串聯(lián)型ADRC方法,定義系統(tǒng)狀態(tài)變量

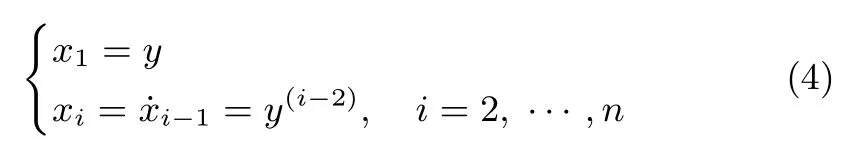
則系統(tǒng)(2)寫成如下狀態(tài)空間方程

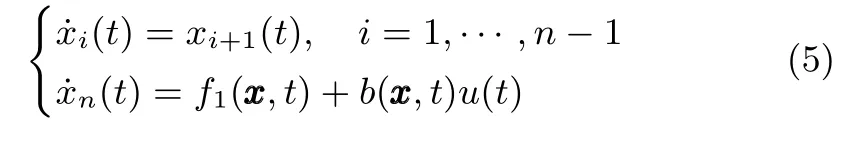
其中,xT=[x1···xn].

假設1.f和b對其自變量的一階偏導數(shù)局部Lipschitz連續(xù).

假設2.b的符號不變,且有

b0是與b具有相同符號的粗略估計.由假設1和假設2,系統(tǒng)(5)可以寫成擴張狀態(tài)方程形式

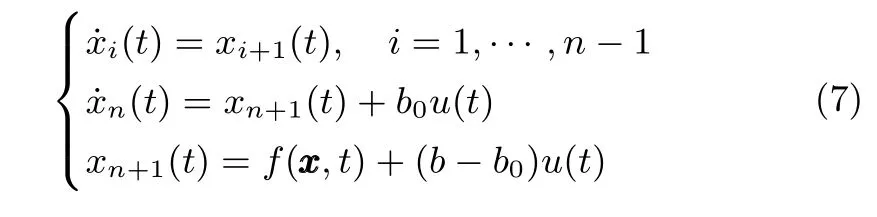
其中,xn+1(t)=f(xx,t)+(b?b0)u(t)為系統(tǒng)的擴張狀態(tài)(Extended state,ES).根據(jù)ADRC理論,式(7)可以通過ESO對xn+1(t)進行估計和補償,實現(xiàn)自抗擾控制.假如采用線性ESO(8),則有引理1.

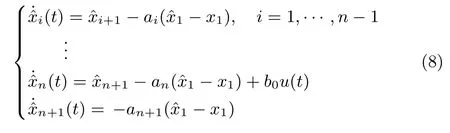
引理 1.系統(tǒng)(7)的線性ESO(8)中的系數(shù)(i=1,···,n+1),其中,為Hurwitz多項式的系數(shù),假設1和假設2成立,則有如下結(jié)論:

1)給定任意正數(shù)tε,對于t∈[tε,∞),下式一致收斂.

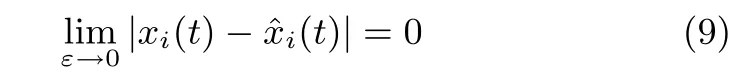
2)系統(tǒng)(7)和系統(tǒng)(8)的解xi和i之差的上極限滿足

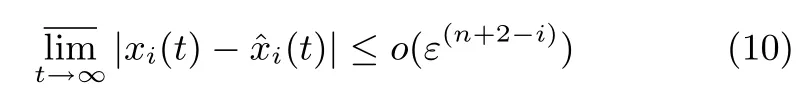
引理1的證明和說明見文獻[11]和文獻[12],引理1中實現(xiàn)了對系統(tǒng)狀態(tài)x的估計,+1實現(xiàn)了對系統(tǒng)總擾動xn+1的估計.據(jù)此可以構(gòu)造如圖1所示的ADRC系統(tǒng)結(jié)構(gòu).

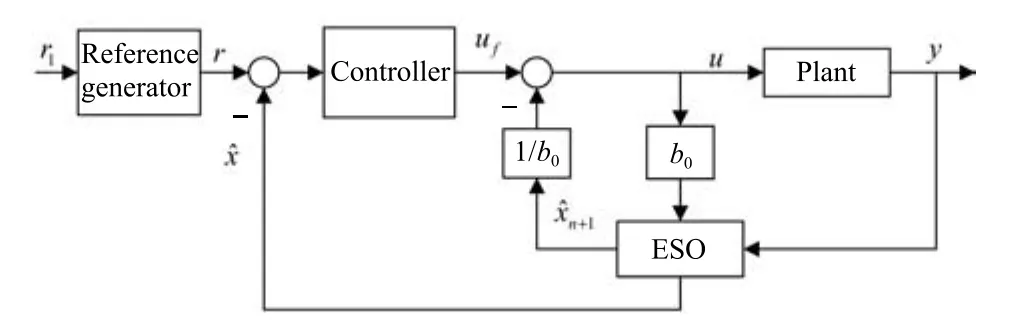
圖1　自抗擾控制的系統(tǒng)結(jié)構(gòu)Fig.1　System structure of ADRC

圖1中,ADRC的關鍵在于通過ESO得到對系統(tǒng)總擾動估計的擴展狀態(tài)n+1,并加入到系統(tǒng)控制輸入中補償系統(tǒng)(5)得到一個近似線性積分串聯(lián)標準型,實現(xiàn)了系統(tǒng)(5)的動態(tài)補償線性化,在此基礎上通過反饋控制uf實現(xiàn)補償后的積分串聯(lián)系統(tǒng)的極點配置,從而保證閉環(huán)系統(tǒng)的性能要求,最終系統(tǒng)的控制量為

由于系統(tǒng)(1)在實際中大量存在,例如過程控制中三容過程,在ADRC的應用中,是否可以直接采用與實際系統(tǒng)更接近的慣性串聯(lián)模型,而不一定是積分串聯(lián)模型呢?同樣采用ADRC的動態(tài)補償線性化思想,但是線性化后得到的不是積分串聯(lián)系統(tǒng),而是與實際系統(tǒng)更接近的慣性串聯(lián)系統(tǒng),可以減少ESO的計算量,更接近實際系統(tǒng)工作時的狀態(tài)變量有明顯的物理意義,其估計值可以用于實際控制系統(tǒng)的故障診斷,有利于提高整個控制系統(tǒng)的可靠性.

2　 慣性串聯(lián)系統(tǒng)的ADRC

針對系統(tǒng)(1),重新定義系統(tǒng)的狀態(tài)變量

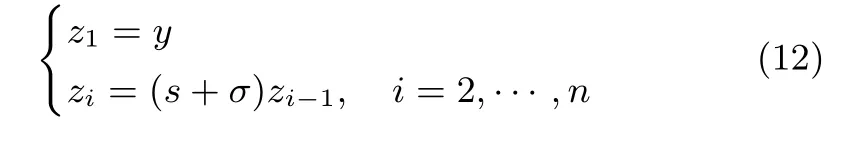
其中,?σ為慣性環(huán)節(jié)的極點,則式(1)可以化為如下的慣性串聯(lián)系統(tǒng)

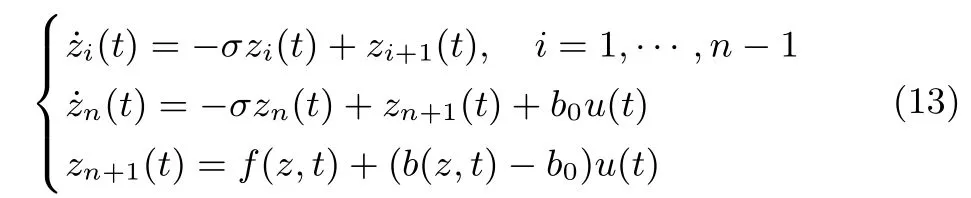
其中,zT=[z1···zn],zn+1(t)為系統(tǒng)的慣性串聯(lián)型ES.對比式(13)和式(5),可以看出積分串聯(lián)系統(tǒng)(5)是慣性串聯(lián)系統(tǒng)(13)當σ=0的特殊情況,仿照積分串聯(lián)型ESO(8)可以構(gòu)造式(13)的ESO為

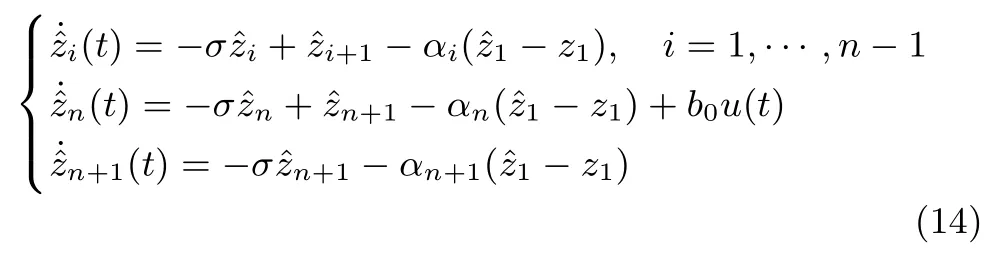
相對于積分串聯(lián)型ESO,式(14)是其推廣,是一種慣性串聯(lián)型ESO.如果慣性串聯(lián)型ESO同樣具有經(jīng)典積分串聯(lián)型ESO對其擴張狀態(tài)的估計的性質(zhì),則系統(tǒng)(1)可以化為圖2所示的慣性串聯(lián)模型.

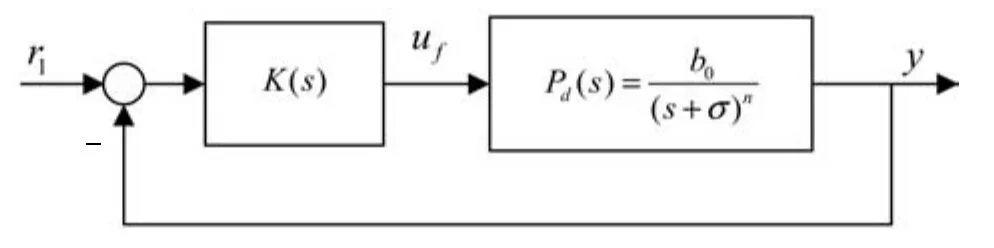
圖2　線性慣性串聯(lián)系統(tǒng)Fig.2　Linear inertia series system

從式(1)可以看出,實際上σ可以取滿足σ≥0的任意值,與實際系統(tǒng)不同的部分可以移到方程的右端,變成f1一部分,慣性串聯(lián)型ESO在估計總擾動的同時,實際上已經(jīng)實現(xiàn)了部分極點配置功能,因此,圖2中的Pd(s)稱為期望模型,而不是標稱模型(或名義模型).標稱模型是盡可能近似被控系統(tǒng)的實際模型,期望模型是盡可能達到控制系統(tǒng)性能指標而人為設計的理想模型.實際應用時,可以根據(jù)閉環(huán)系統(tǒng)的性能指標來選擇期望模型Pd(s)中的σ,然后根據(jù)分離原理,分別設計慣性串聯(lián)型ESO和反饋控制器K(s).

2.1　慣性串聯(lián)系統(tǒng)ESO

對于慣性串聯(lián)系統(tǒng)ESO有如下定理:

定理1.假設慣性串聯(lián)型ESO系統(tǒng)(14)中的系數(shù)αi=,其中,0＜ε≤1,i為Hurwitz多項式的系數(shù),系統(tǒng)滿足假設1和假設2,則有如下結(jié)論:

1)給定任意正數(shù)tε,對于t∈[tε,∞)下式一致收斂.

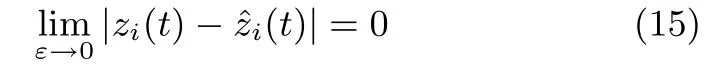
2)系統(tǒng)(13)和系統(tǒng)(14)的解zi和i之差的上極限滿足

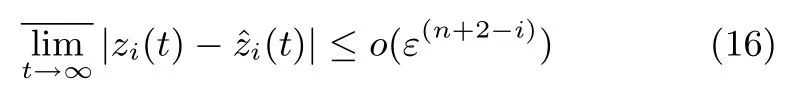
其中,i=1,···,n+1,zn+1(t)=f+(b?b0)u(t) 為系統(tǒng)(13)的擴張狀態(tài).

證明.根據(jù)式(4)和式(12)的兩種狀態(tài)變量的定義,狀態(tài)變量之間的關系為

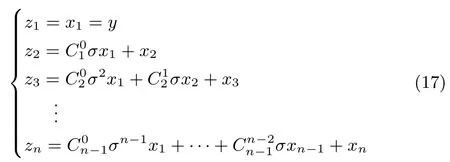
式(17)寫成向量和矩陣形式為

其中,T為可逆變換矩陣

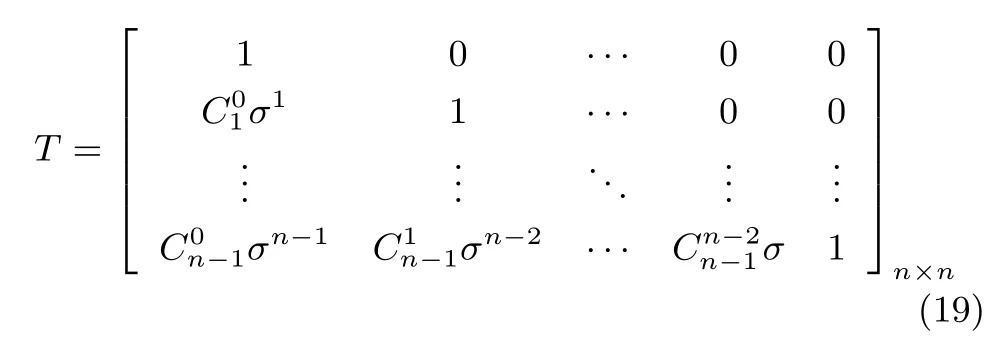
同理有

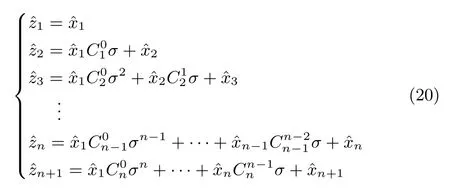
式(20)寫成向量和矩陣形式為

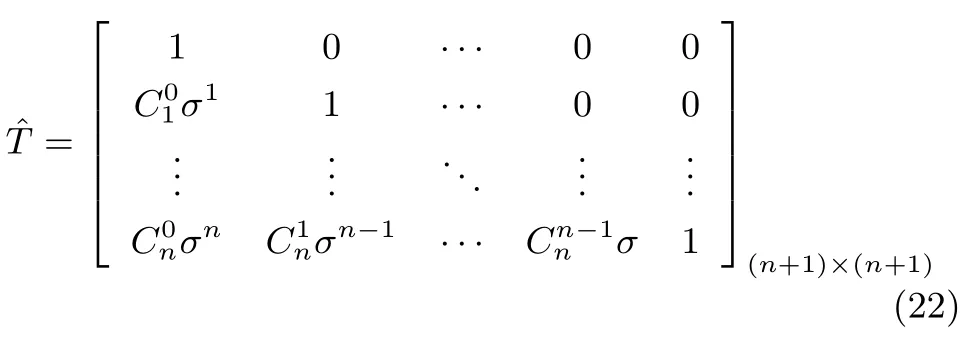
根據(jù)引理1,采用線性ESO(8)對式(2)的狀態(tài)進行估計,式(9)和式(10)成立,則有

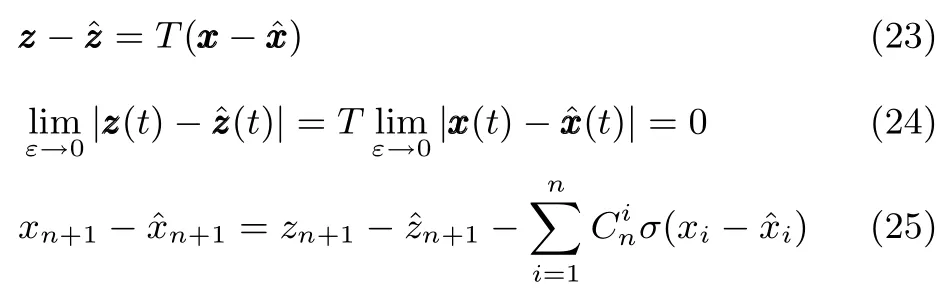
式(25)兩邊取絕對值有

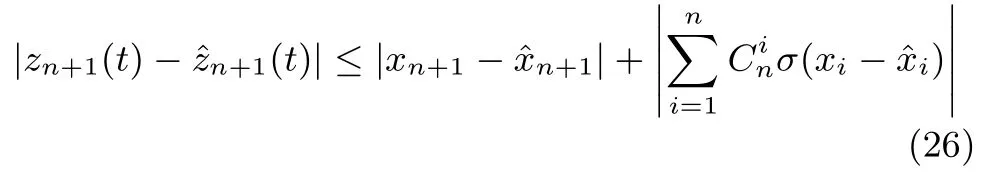
由式(9)和式(24)有

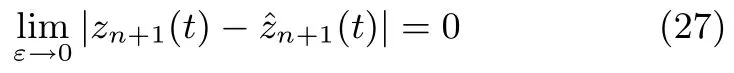
即定理1中的式(15)成立.同理,由式(17)、式(20)和式(25)以及高階無窮小的概念有

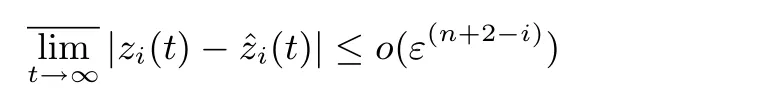
即定理1中的式(16)成立.□

2.2　慣性串聯(lián)型自抗擾控制

采用慣性串聯(lián)型ESO進行動態(tài)補償線性化的同時,還進行被控對象的期望極點配置,把實際的非線性被控對象模型變?yōu)槠谕木€性被控對象模型.由圖2可得到閉環(huán)系統(tǒng)的傳遞函數(shù)為

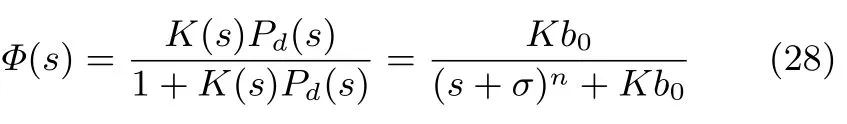
可以根據(jù)式(28)的閉環(huán)系統(tǒng)期望極點直接選擇σ和K.對于跟蹤問題,還可以引入?yún)⒖驾斎氲那梆伩刂屏?改善跟蹤性能.

圖3是在經(jīng)典ADRC理論基礎上,采用慣性串聯(lián)型ESO和增加參考軌跡的高階導數(shù)作為前饋控制量后的慣性串聯(lián)型ADRC,其控制輸入為

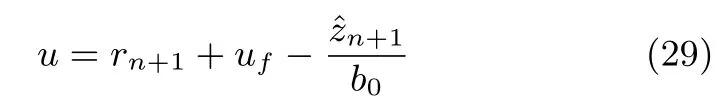
若采用PD反饋控制,則有

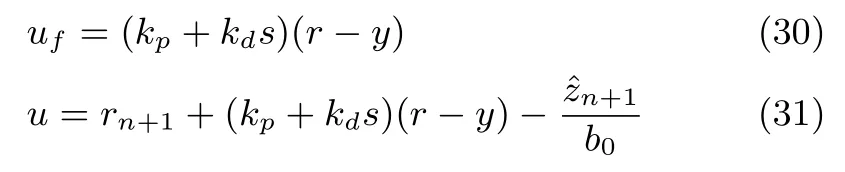
其中,kp＞0和kd＞0為反饋控制的比例增益和微分增益.

圖3　慣性串聯(lián)型自抗擾控制結(jié)構(gòu)Fig.3　ADRC topology for inertia series system

從圖1和圖3可以看出,經(jīng)典ADRC和慣性串聯(lián)型ADRC是具有三自由度(3-degree of freedom,3-DOF)的控制系統(tǒng),第一個自由度對輸入信號的過渡過程進行規(guī)劃,可以采用ADRC技術(shù)之一的跟蹤微分器(Tracking differentiator,TD)來實現(xiàn),解決快速跟蹤性和系統(tǒng)超調(diào)之間的矛盾;第二個自由度為ESO,實現(xiàn)動態(tài)非線性補償以克服外部干擾和內(nèi)部模型不確定性影響,把非線性時變不確定系統(tǒng)劃分積分串聯(lián)或者慣性串聯(lián)確定系統(tǒng);第三個自由度為反饋控制器,可以采用非線性或者線性控制器,雖然韓京清在其原著中采用了大量的非線性控制方法,但由于線性控制器比較簡單,在實際應用中被大量選用.與圖1的ADRC不同的是,圖3的慣性串聯(lián)型ADRC中系統(tǒng)狀態(tài)zi的估計狀態(tài)i不再是被控對象輸出y的直接求導,需要經(jīng)過式(17)的反變換才能用于得到系統(tǒng)輸出的導數(shù),用于式(31)中控制量的計算.

與經(jīng)典ADRC一樣,慣性串聯(lián)型ADRC中也可以包含已有模型知識,處理方法與經(jīng)典ADRC類似,圖4為部分模型已知的慣性串聯(lián)型ADRC,為模型已知的部分,分別作為了慣性串聯(lián)型ESO和系統(tǒng)控制輸入的一部分.

對于部分模型已知的慣性串聯(lián)型ADRC,其ESO為

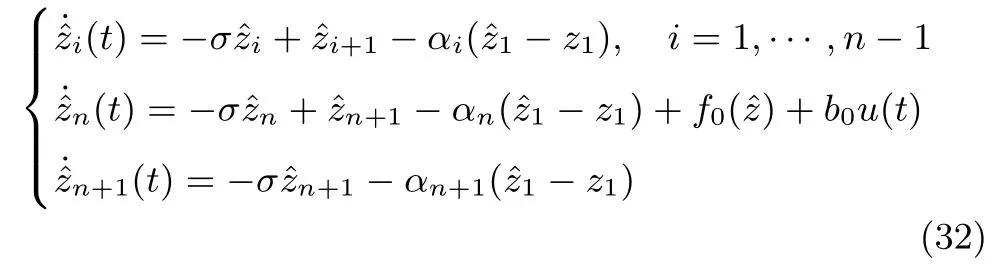
相應地,系統(tǒng)的控制輸入為

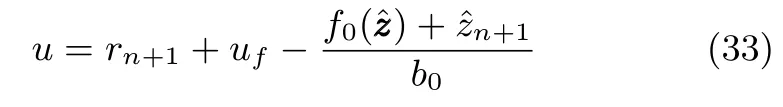
2.3　 慣性串聯(lián)型ADRC與基于DOB的控制

基于DOB的控制方法是另一種典型的抗擾動控制方法[22?23],圖5(a)給出經(jīng)典DOB原理圖,圖5(b)是其等效電路圖.圖5中,Pn(s)為標稱模型,Q(s)為低通濾波器,P(s)為被控對象傳遞函數(shù)且有

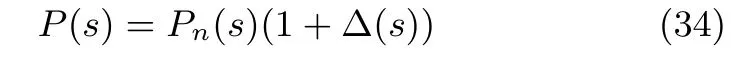
其中,?(s)為傳遞函數(shù)的建模誤差.基于DOB的控制的系統(tǒng)輸入和輸出為

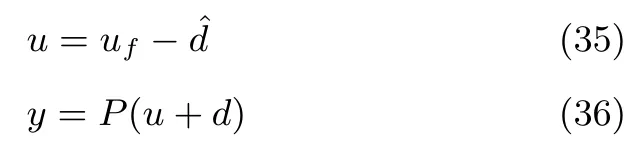
其中,uf為反饋控制量,為系統(tǒng)模型不匹配?(s)和外部擾動d對系統(tǒng)輸出總影響的從系統(tǒng)輸入等效的總擾動估計.系統(tǒng)輸出和總擾動的傳遞函數(shù)為

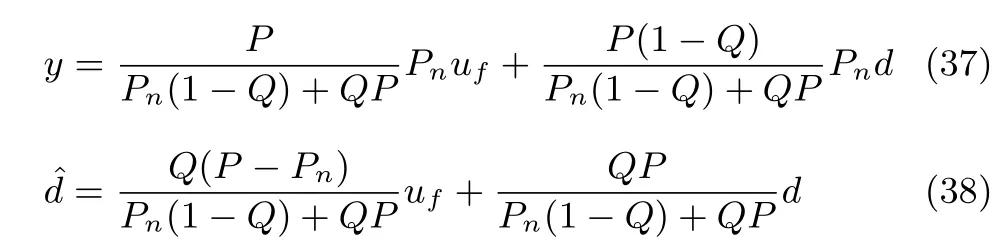
其中,式(38)的第1項為由被控對象模型和標稱模型不匹配引起的內(nèi)部擾動,第2項為外部干擾輸入d引起的外部擾動.

從圖3和圖5可以看出,若在基于DOB的控制系統(tǒng)中也增加對系統(tǒng)參考輸入過渡過程的規(guī)劃,可以看出,雖然慣性串聯(lián)型ADRC和基于DOB的控制對被控系統(tǒng)輸入輸出信息的利用方式不同,但是ADRC和基于DOB的控制都為3-DOF控制系統(tǒng)結(jié)構(gòu),它們都把被控系統(tǒng)的內(nèi)部模型以外的系統(tǒng)輸出部分等效到系統(tǒng)輸入作為對系統(tǒng)總擾動的估計,并用此總擾動估計實現(xiàn)對系統(tǒng)的補償控制.從抗擾控制的發(fā)展過程來看,ADRC起初是在時域中提出和研究,它把狀態(tài)估計思想發(fā)展為擴張狀估計器,估計出系統(tǒng)總擾動并在系統(tǒng)輸入進行補償,實現(xiàn)抗擾.由于DOBC和ADRC的結(jié)構(gòu)類似,DOBC也具有對總擾動進行估計和補償功能[24].對于慣性串聯(lián)型ADRC和基于DOB控制的定量關系有如下定理.

定理2.取慣性串聯(lián)型ADRC的期望系統(tǒng)模型Pd(s)為DOB的標稱模型Pn(s),即

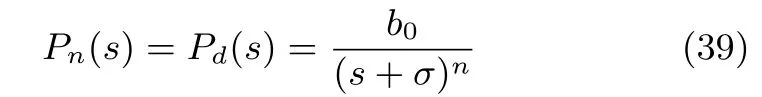
同時基于DOB的控制系統(tǒng)中低通濾波器Q(s)取為

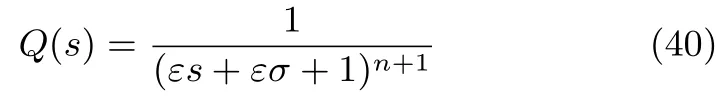
則有如下等式成立

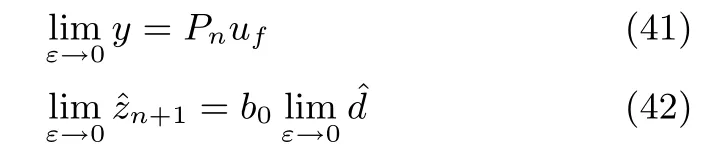
即基于DOB的控制與慣性串聯(lián)型ADRC是統(tǒng)一的,它們具有相同的補償控制機制.

證明.低通濾波器Q(s)當ε→0的極限為

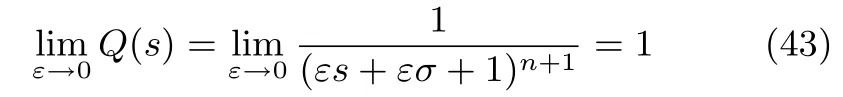
則根據(jù)式(37)有

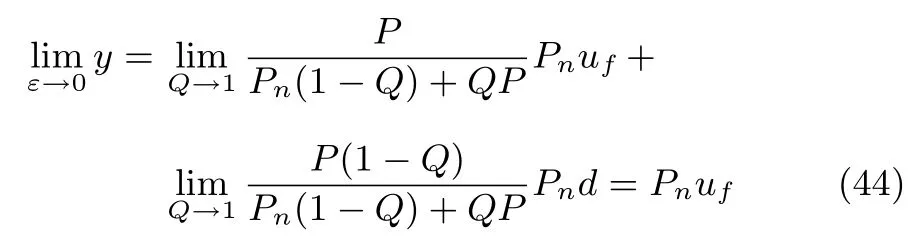
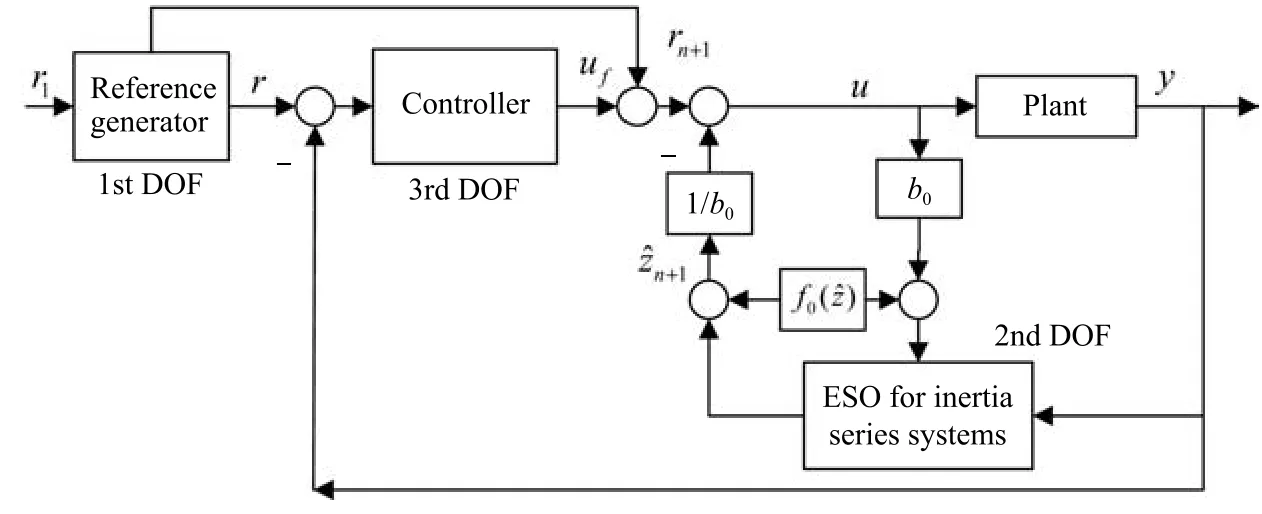
圖4　部分模型已知的慣性串聯(lián)型自抗擾控制結(jié)構(gòu)Fig.4　ADRC topology for inertia series systems with partially known model

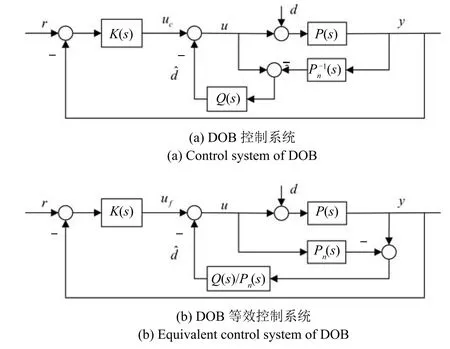
圖5　基于DOB的控制的系統(tǒng)框圖Fig.5　Block diagram of DOB control system

同理,根據(jù)式(38)有

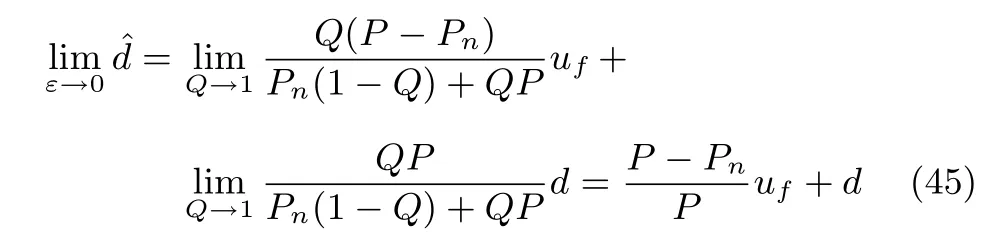
由定理1的結(jié)論并結(jié)合式(42)有

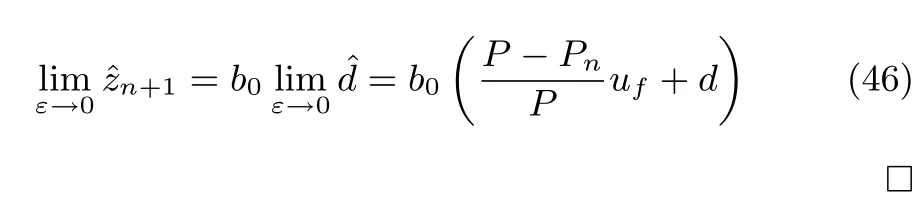
定理2說明:

1)慣性串聯(lián)型ESO和DOB都實現(xiàn)了對系統(tǒng)期望模型(或者系統(tǒng)內(nèi)模)以外總擾動的估計,它們都把被控系統(tǒng)的輸入和輸出數(shù)據(jù)分別為兩部分,一部分是期望模型產(chǎn)生的,另一部分是期望模型不能解釋的,由系統(tǒng)外部擾動和系統(tǒng)模型其余部分(不包含期望模型)一起產(chǎn)生的,并在被控系統(tǒng)的輸入側(cè)等效為系統(tǒng)總擾動.因此,抗擾控制本質(zhì)上是主成分分析(Principal component analysis,PCA)思想在動態(tài)系統(tǒng)和控制理論中的應用,把被控系統(tǒng)的輸入輸出數(shù)據(jù)分別投影到期望模型空間和期望模型的補空間.ESO和DOB都有大量的實際應用案例,相比DOB,ESO除了系統(tǒng)總擾動的估計,還可以得到系統(tǒng)輸出的各階導數(shù),而且ADRC對非線性系統(tǒng)有嚴格的理論證明[6?9].定理2給出的ESO和DOB的內(nèi)在聯(lián)系可以使得兩種抗擾動控制方法相互引入對方的研究成果,共同發(fā)展.

2)經(jīng)典ADRC的期望模型為積分串聯(lián)模型,其極點為0;基于DOB的控制的期望模型為標稱模型[25?26],一般通過機理建模或系統(tǒng)辨識方法確定,反應了實際被控對象的動態(tài)特性.慣性串聯(lián)型ADRC的期望模型是根據(jù)閉環(huán)控制系統(tǒng)的性能指標來確定,可以是積分串聯(lián)模型,也可以是標稱模型,還可以是其他任何滿足用戶性能要求的穩(wěn)定系統(tǒng)模型,采用期望模型可以充分利用系統(tǒng)模型已有知識,把已有知識在期望模型中顯示表示,降低了擴張狀態(tài)觀測器的帶寬和計算量,方便調(diào)節(jié)控制系統(tǒng)參數(shù).

3　仿真研究

考慮如下的二階非線性不確定系統(tǒng)

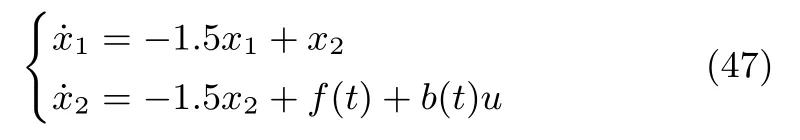
系統(tǒng)(47)的輸入為u,x1和x2為系統(tǒng)狀態(tài),系統(tǒng)輸出為y1.為了仿真量測噪聲對控制性能的影響,在系統(tǒng)輸出中增加高頻量測噪聲,y1=x1+0.003sin(100t),假設系統(tǒng)(47)中的f(t)和b(t)滿足定理1的條件,但是結(jié)構(gòu)和參數(shù)都未知.仿真時取

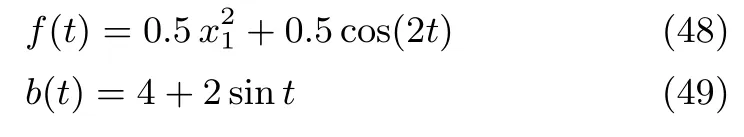
控制的目標是使系統(tǒng)的輸出x1跟蹤參考軌跡r1.假設系統(tǒng)需要跟蹤的參考軌跡為

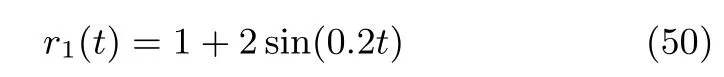
系統(tǒng)(47)為非線性慣性串聯(lián)系統(tǒng),假設b(t)的粗略估計為b0=4.對于系統(tǒng)(47)的控制,采用定理1的慣性串聯(lián)型ESO補償系統(tǒng)(47)為近似線性系統(tǒng)且把補償后的線性系統(tǒng)的二重極點配置為σ=0.4,取ESO的工作參數(shù)分別為:ε=0.08,1=3,2=3,3=1.系統(tǒng)(47)經(jīng)過ESO補償后的傳遞函數(shù)為

進一步,圖3的ADRC可以等效為狀態(tài)方程形式

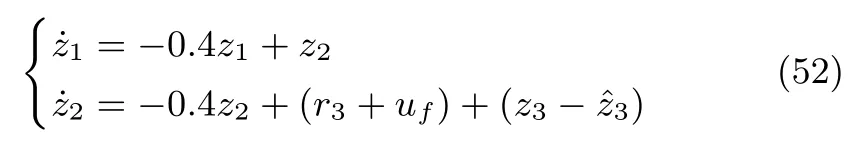
其中,r3和uf分別為參考輸入(50)的二階導數(shù)和反饋控制量.ESO把非線性系統(tǒng)(47)實時補償為具有期望極點的線性系統(tǒng).慣性串聯(lián)系統(tǒng)系統(tǒng)(52)的擴張狀態(tài)z3為

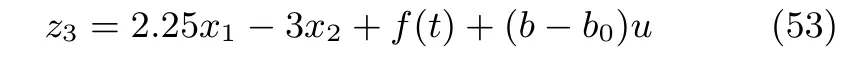
采用式(31)的ADRC控制量,且采用反饋控制為PD控制,取kp=20和kd=5.

圖6給出了參考輸入和系統(tǒng)輸出變化曲線,可以看出,慣性串聯(lián)型ADRC實現(xiàn)了系統(tǒng)輸出很好地跟蹤了參考輸入.圖7是系統(tǒng)的控制輸入,控制輸入除了在初始時刻有因峰值現(xiàn)象引起的跳躍之后是光滑的,可以看出,初始峰值現(xiàn)象在慣性串聯(lián)系統(tǒng)中減弱了,還可以進一步把初始時刻的控制設置為零,延時一段時間(以避開初始峰值)后才輸出系統(tǒng)控制的方法解決[27?28].

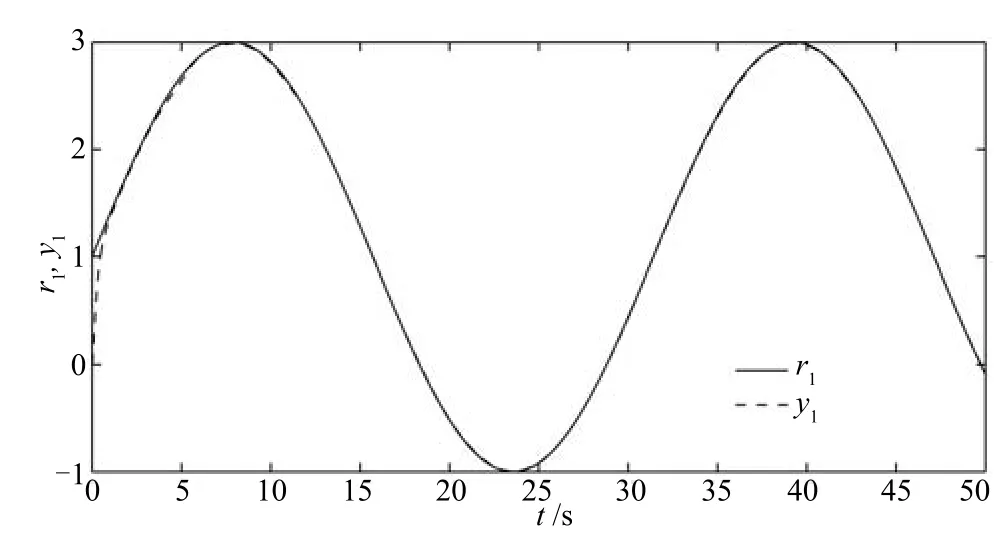
圖6　參考輸入r1和系統(tǒng)輸出y1Fig.6　Reference inputr1and system outputy1

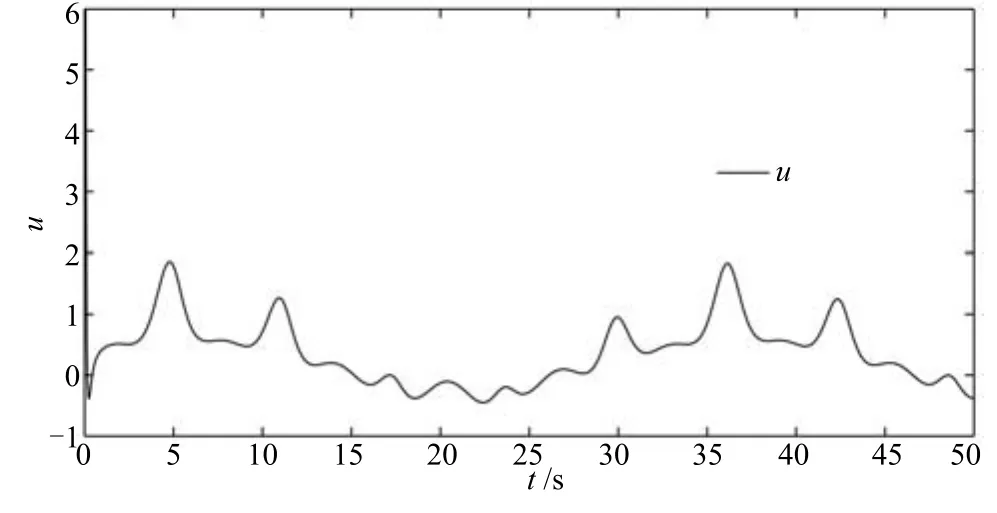
圖7　系統(tǒng)控制輸入uFig.7　System inputu

圖8是慣性串聯(lián)型ESO對系統(tǒng)擴張狀態(tài)z3的估計3的跟隨情況,從圖8可知,除了由初始狀態(tài)引起的峰值現(xiàn)象外,3實現(xiàn)了對z3的良好跟蹤.

經(jīng)典的ADRC先把被控對象的極點配置到原點,然后通過反饋控制把位于原點的極點配置到期望的位置.由于實際系統(tǒng)本身的極點大多位于左半平面,經(jīng)典ADRC采用兩次方向不一致的極點配置方法增加了計算量,采用慣性串聯(lián)型ESO在原有極點位置的基礎上按照控制目標進行適當調(diào)整能夠集成已有模型知識,還可以通過已知模型輸出與慣性串聯(lián)型ESO估計的誤差來判斷控制系統(tǒng)是否有故障,實現(xiàn)控制系統(tǒng)的故障診斷,提高整個控制系統(tǒng)的可靠性,這是下一步的研究工作.

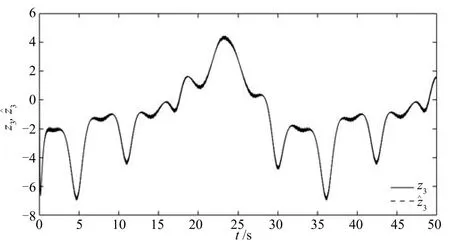
圖8　系統(tǒng)(47)的擴張狀態(tài)z3及其估計3Fig.8ESz3and its estimation3of system(47)

4　結(jié)論

本文提出的慣性串聯(lián)系統(tǒng)的ADRC控制,是經(jīng)典積分串聯(lián)型ADRC的推廣,同樣具有經(jīng)典ADRC對系統(tǒng)總擾動的估計性能,慣性串聯(lián)型ADRC能更好地利用已有系統(tǒng)的知識,減少ESO的計算量.本文還對慣性串聯(lián)型ADRC和基于DOB的控制之間的關系進行了研究,指出它們具有相同的結(jié)構(gòu)和模塊功能的3-DOF控制系統(tǒng),并給出了它們之間的定量關系.仿真研究表明所提出的慣性串聯(lián)型ADRC方式是有效的.如何利用慣性串聯(lián)型ESO實現(xiàn)控制系統(tǒng)的故障診斷是下一步的研究工作.

1 Han Jing-Qing.Auto-disturbances-rejection controller and it.s applications.Control and Decision,1998,13(1):19?23(韓京清.自抗擾控制器及其應用.控制與決策,1998,13(1):19?23)

2 Han J Q.From PID to active disturbance rejection control.IEEE Transactions on Industrial Electronics,2009,56(3):900?906

3 Gao Z Q.Active disturbance rejection control:a paradigm shift in feedback control system design.In:Proceedings of the 2006 American Control Conference.Minneapolis,MN,USA:IEEE,2006.2399?2405

4 Huang Y,Xue W C.Active disturbance rejection control:methodology and theoretical analysis.ISA Transactions,2014,53(4):963?976

5 Gao Z Q.Active disturbance rejection control:from an enduring idea to an emerging technology.In:Proceedings of the 10th International Workshop on Robot Motion and Control.Poznan,Poland:IEEE,2006.269?282

6 Gao Z Q.Scaling and bandwidth-parameterization based controller tuning.In:Proceedings of the 2003 American Control Conference.Denver,USA:IEEE,2003.4989?4996

7 Zhao Z L,Guo B Z.Extended state observer for uncertain lower triangular nonlinear systems.Systems and Control Letters,2015,85:100?108

8 Guo B Z,Zhao Z L.On convergence of the nonlinear active disturbance rejection control for MIMO systems.SIAM Journal on Control and Optimization,2013,51(2):1727?1757

9 Wu Lei,Bao Hong,Du Jing-Li,Wang Cong-Si.A learning algorithm for parameters of automatic disturbances rejection controller.Acta Automatica Sinica,2014,40(3):556?560(武雷,保宏,杜敬利,王從思.一種自抗擾控制器參數(shù)的學習算法.自動化學報,2014,40(3):556?560)

10 Zheng Q,Gao L Q,Gao Z Q.On validation of extended state observer through analysis and experimentation.Journal of Dynamic Systems,Measurement,and Control,2012,134(2):024505

11 Guo B Z,Zhao Z L.On the convergence of an extended state observer for nonlinear systems with uncertainty.Systems and Control Letters,2011,60(6):420?430

12 Yangxx,Huang Y.Capabilities of extended state observer for estimating uncertainties.In:Proceedings of the 2009 American Control Conference.St.Louis,MO,USA:IEEE,2009.3700?3705

13 Zhou W K,Shao S,Gao Z Q.A stability study of the active disturbance rejection control problem by a singular perturbation approach.Applied Mathematical Sciences,2009,3(10):491?508

14 Xue W C,Huang Y.On frequency-domain analysis of ADRC for uncertain system.In:Proceedings of the 2013 American Control Conference.Washington,DC,USA:IEEE,2013.6637?6642

15 Chen Zeng-Qiang,Sun Ming-Wei,Yang Rui-Guang.On the stability of linear active disturbance rejection control.Acta Automatica Sinica,2013,39(5):574?580(陳增強,孫明瑋,楊瑞光.線性自抗擾控制器的穩(wěn)定性研究.自動化學報,2013,39(5):574?580)

16 Guo B Z,Zhao Z L.On convergence of nonlinear active disturbance rejection for SISO systems.In:Proceedings of the 24th Chinese Control and Decision Conference.Taiyuan,China:IEEE,2012.3507?3512

17 Cheng Chun-Hua,Hu Yun-An,Wu Jin-Hua.Auto disturbance controller of non-affine nonlinear pure feedback systems.Acta Automatica Sinica,2014,40(7):1528?1536(程春華,胡云安,吳進華.非仿射純反饋非線性系統(tǒng)的自抗擾控制.自動化學報,2014,40(7):1528?1536)

18 Guo B Z,Zhao Z L.On convergence of tracking differentiator.International Journal of Control,2011,84(4):693?701

19 Xue W C,Huang Y,Yangxx.What kinds of system can be used as tracking-differentiator.In:Proceedings of the 29th Chinese Control Conference.Beijing,China:IEEE,2010.6113?6120

20 Li Jie,Qi Xiao-Hui,Xia Yuan-Qing,Gao Zhi-Qiang.On linear/nonlinear active disturbance rejection switching control.Acta Automatica Sinica,2016,42(2):202?212(李杰,齊曉慧,夏元清,高志強.線性/非線性自抗擾切換控制方法研究.自動化學報,2016,42(2):202?212)

21 Guo B Z,Zhao Z L.On convergence of non-linear extended state observer for multi-input multi-output systems with uncertainty.IET Control Theory and Applications,2012,6(15):2375?2386

22 Schrijver E,van Dijk J.Disturbance observers for rigid mechanical systems:equivalence,stability,and design.Journal of Dynamic Systems,Measurement,and Control,2002,124(4):539?548

23 Shimh,Joo Y J.State space analysis of disturbance observer and a robust stability condition.In:Proceedings of the 46th IEEE Conference on Decision and Control.New Orleans,LA,USA:IEEE,2007.2193?2198

24 Xue W C,Huang Y.Comparison of the DOB based control,a special kind of PID control and ADRC.In:Proceedings of the 2011 American Control Conference.San Francisco,CA,USA:IEEE,2011.4373?4379

25 Yu Zhe,Wang Lu,Su Jian-Bo.Disturbance observer based control for linear multi-variable systems with uncertainties.Acta Automatica Sinica,2014,40(11):2643?2649(于哲,王璐,蘇劍波.基于干擾觀測器的不確定線性多變量系統(tǒng)控制.自動化學報,2014,40(11):2643?2649)

26 Shimh,Jo Nh.An almost necessary and sufficient condition for robust stability of closed-loop systems with disturbance observer.Automatica,2009,45(1):296?299

27 Cunha J P V S,Costa R R,Lizarralde F,Hsu L.Peaking free variable structure control of uncertain linear systems based on a high-gain observer.Automatica,2009,45(5):1156?1164

28 Xue W C,Huang Y.On performance analysis of ADRC for nonlinear uncertain systems with unknown dynamics and discontinuous disturbance.In:Proceedings of the 32nd Chinese Control Conference.Xi′an,China:IEEE,2013.1102?1107