基于半正定規劃的壓縮感知線陣三維SAR自聚焦成像算法

韋順軍 田博坤 張曉玲 師 君

(電子科技大學電子工程學院 成都 611731)

1 引言

合成孔徑雷達(Synthetic Aperture Radar，SAR)作為一種具有全天時、全天候、高分辨力、大區域觀測及信息量豐富的雷達成像技術，已成為當今遙感對地觀測的重要手段。因具備3維成像能力，線陣SAR (Linear Array Synthetic Aperture Radar， LASAR)是近幾年來被廣泛關注的一種新體制SAR 3維成像技術[1-4]。本質上，LASAR主要利用線陣天線運動合成一個大的虛擬2維陣列實現觀測目標的2維分辨，再利用距離脈沖壓縮技術實現觀測目標的3維成像。相對于其它常規SAR 3維成像體制(如圓周SAR、層析SAR等)， LASAR具備成像模式多樣、應用靈活等優勢，克服了常規SAR 3維成像體制無法下視、前視成像的缺陷，在城市地形測繪、飛行器導航及盲降、目標精定位與識別、戰場情報獲取等民用和軍用領域具有重要的研究價值和應用前景。

目前，LASAR 3維成像處理主要采用基于匹配濾波理論的成像算法[1，2]，如距離多普勒算法和后向投影算法。受載荷平臺(如飛機、無人機、衛星等)空間及線陣天線長度限制，傳統匹配濾波成像算法在LASAR線陣方向的分辨能力通常比其它維向的分辨力低，一定程度約束了LASAR高分辨成像應用。然而，由于地面、空中等觀測目標在3維空間通常具有強稀疏性，故可利用目標稀疏先驗信息提升LASAR 3維成像精度。近幾年，基于壓縮感知(Compressed Sensing， CS)理論的稀疏成像已經成為LASAR高分辨成像的研究熱點之一，并提出了多種基于CS稀疏重構的LASAR 3維高分辨稀疏成像方法[5-8]。但是，CS稀疏重構對成像模型的精確性要求非常高，如在X波段雷達時位置精度通常需要達到毫米級，現有壓縮感知LASAR 3維稀疏成像算法通常以成像模型精確已知為前提，并沒有考慮實際平臺運動誤差的影響。當LASAR存在運動誤差、陣列抖動時，則會導致成像模型存在偏差，CS稀疏重構出現散焦、畸變、虛假目標等成像質量惡化現象，甚至不能成像。另外，與傳統SAR系統單個或少量天線工作不同，LASAR需要成百上千天線陣元同時工作，故僅利用雷達系統中單個位置的導航測量系統(如IMU(Inertial Measurement Unit)系統、GPS (Global Positioning System)或北斗系統)數據難以實現LASAR多個天線陣元運動誤差的精確補償。為了提高壓縮感知LASAR 3維成像質量，在利用導航測量數據進行運動誤差補償后，還需結合回波數據和自聚焦成像技術實現多天線陣元的殘余運動誤差補償。

至今，針對傳統SAR成像中的運動誤差補償，相關學者已經提出了多種基于不同準則的自聚焦成像算法，如最大似然估計(Maximum Likelihood Estimation， MLE)自聚焦、最小熵估計(Minimum Entropy Estimation， MEE)自聚焦、最大銳度(Maximum Sharpness Estimation， MSE)自聚焦等方法。相位梯度自聚焦(Phase Gradient Autofocus，PGA)算法作為一種在SAR實際成像中廣泛應用的典型MLE自聚焦成像算法，已被成功用于壓縮感知SAR稀疏成像中的殘余相位誤差補償[9]。但是，當回波數據欠采樣時，傳統自聚焦算法不一定適用于壓縮感知SAR稀疏自聚焦成像[10]。針對壓縮感知SAR 稀疏自聚焦問題，近幾年相關學者也已經提出一些解決方法。文獻[11]提出了一種基于稀疏驅動的聯合SAR稀疏成像及相位誤差校正方法，采用迭代估計方法求解非二次正則化問題實現SAR稀疏自聚焦成像。文獻[12]提出一種針對稀疏微波成像的自聚焦方法，采用貪婪算法實現相位誤差的高精度估計。文獻[13]提出了一種基于子孔徑參數稀疏表示的機載SAR自聚焦成像算法，實測數據結果表明該方法相對于傳統PGA算法具有更好的自聚焦性能。文獻[14]針對運動誤差造成的網格偏離現象，提出了一種基于稀疏重構的聚束式SAR自聚焦成像算法，采用正交匹配追蹤及最速下降法實現稀疏自聚焦成像。另外，還有一些文獻提出基于其它準則或估計模型的SAR 稀疏自聚焦算法[15-17]。然而，與傳統SAR運動誤差形式不同，由于受線陣稀疏分布及平臺顫動、線陣抖動等聯合運動誤差影響，LASAR成像模型中相位誤差具有多維度、高階項分布等更復雜的形式，現有 SAR稀疏自聚焦算法不一定適用于LASAR自聚焦成像。對此，本文作者也提出了基于稀疏貝葉斯學習的LASAR自聚焦成像算法，在欠采樣數據條件下可有效估計相位誤差[18，19]，但是該方法需已知目標及相位的先驗分布特性并且要求較高的回波信噪比條件。

為了補償欠采樣條件下LASAR多維度高階相位誤差，本文提出了一種基于半正定規劃(Semi-Definite Programming， SDP)的壓縮感知LASAR自聚焦成像算法，即半正定規劃自聚焦(Semi-Definite Programming Sparse Autofocus， SDPSA)算法，簡稱為SDPSA算法。該方法利用LASAR壓縮感知成像原理、圖像最大銳度及最小均方誤差準則，構造了欠采樣條件下稀疏目標相位誤差估計模型，并通過松弛半正定規劃及迭代逼近方法實現壓縮感知LASAR的高精度稀疏自聚焦成像。為了進一步提高SDPSA算法自聚焦運算效率，利用主散射目標區域提取，僅采用主散射區域進行相位誤差估計。仿真數據和實測數據驗證了本文SDPSA算法的有效性，相對于PGA自聚焦算法，SDPSA算法在欠采樣數據時具有更好的成像質量。本文的主要結構如下：第2節簡單介紹了壓縮感知LASAR成像模型和稀疏成像原理，闡述了其陣列多相位中心的相位誤差影響；第3節建立LASAR相位誤差估計的半正定規劃模型，提出了基于半正定規劃的壓縮感知LASAR稀疏自聚焦成像方法，并介紹了該方法的基本步驟；第4節利用LASAR仿真及實測數據，分析SDPSA稀疏自聚焦成像算法性能，驗證了算法的有效性；第5節給出了本文算法的主要結論。

2 壓縮感知LASAR成像原理

2.1 回波線性測量模型

LASAR 3維成像的典型幾何模型如圖1所示，其中X， Y和Z軸分別表示切航跡、沿航跡和高度向，線陣天線平行于X軸放置。假設LASAR系統工作于正下視成像模式，表示合成孔徑時間內LASAR合成的2維等效陣列天線相位中心(Antenna Phase Center， APC)位置集，為2維APC總個數，，和分別為第個APC位置的X， Y和Z軸位置。在遠場條件下，LASAR觀測場景可近似為點散射模型，并對觀測場景進行3維離散化。令分別表示LASAR離散觀測場景的位置集和散射系數集，其中為觀測場景的散射單元序列，為散射單元總數，，和分別為第個散射單元的X，Y和Z軸位置，為的散射系數。

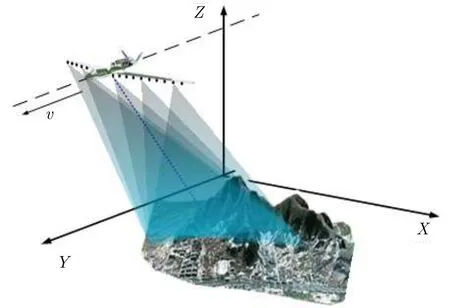
圖1 LASAR正下視3維成像的幾何模型Fig. 1 The geographic model of down-looking LASAR imaging

假設LASAR系統發射線性調頻信號，其原始回波經過距離壓縮后，散射單元回波信號可表示為：

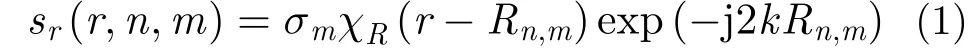
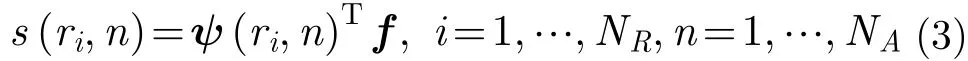
2.2 CS稀疏成像

CS理論指出當信號可稀疏表示時，可利用遠低于Nyquist采樣率進行采樣，將原始信號重構問題轉化為線性約束最優化求解問題，實現稀疏信號的精確重構[20]。若LASAR觀測場景散射系數具有稀疏特征，根據CS稀疏重構理論，散射系數可通過求解如下范數最優化問題進行重構：

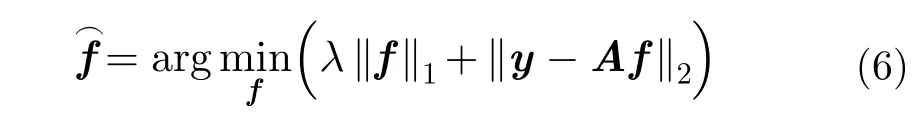
2.3 相位誤差

由于受平臺顫動、線陣抖動等聯合運動誤差影響，LASAR 2維APC存在位置誤差，會導致 LASAR成像模型存在多維度、高階項分布的復雜相位誤表示LASAR回波數據中2維APC位置不確定引起的相位誤差向量，此時LASAR回波信號的線性測量模型表示為：

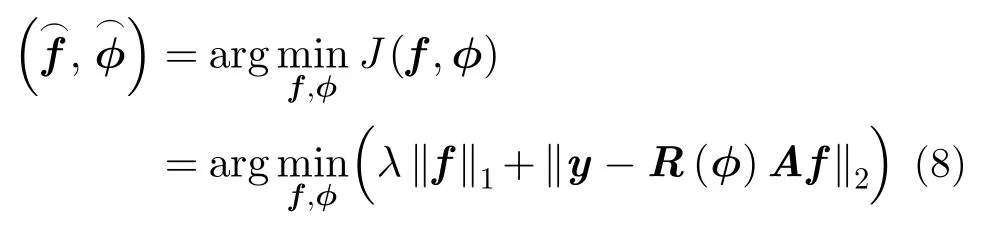
若線陣天線陣元稀疏分布或回波信號欠采樣，LASAR自聚焦稀疏本質上是一個病態求逆問題，直接求解最優化問題十分困難。目前，稀疏自聚焦算法通常采用基于某個準則的迭代算法以。如，文獻[11，13]采用稀疏重構聯合最小MSE 準則實現SAR稀疏自聚焦，文獻[19]采用最大后驗概率準則實現稀疏自聚焦，而不同稀疏自聚焦準則具有不同的優劣及特點。

3 半正定規劃稀疏自聚焦成像

3.1 半正定規劃自聚焦原理

為了實現欠采樣數據條件下LASAR稀疏自聚焦，聯合壓縮感知LASAR成像原理、圖像最大銳度及最小均方誤差重構準則，本文提出一種基于半正定規劃的LASAR稀疏自聚焦成像算法。該方法采用迭代估計方法，給定估計初值及參數后，主要由稀疏目標重構、相位誤差估計兩個獨立過程循環實現，其具體理論推導及實現過程如下。

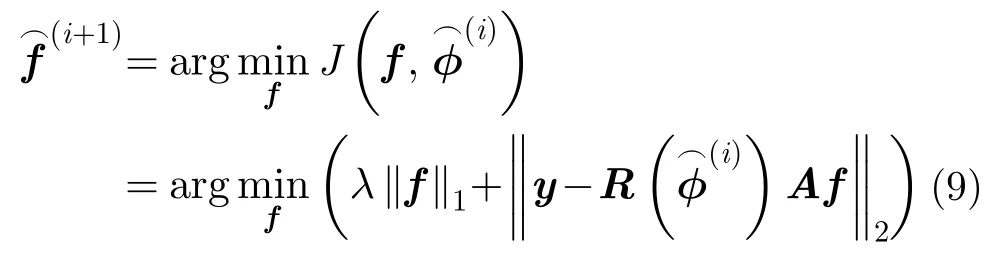
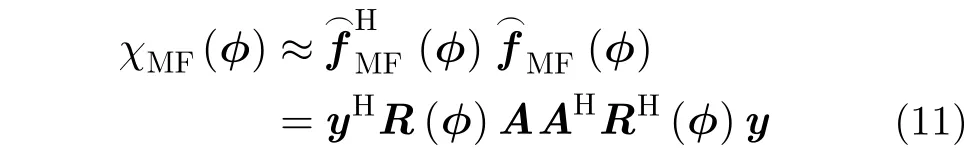
對于最小MSE準則，根據式(9)，回波數據的重構MSE表示為：

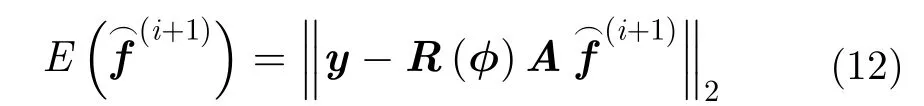
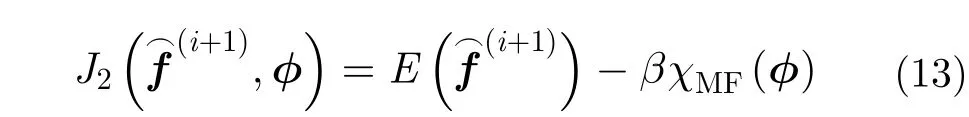
顯然，式(18)最優化問題可采用恒定常數二次規劃(Constant Modulus Quadratic Programming，CMQP)方法求解。相位誤差向量的最優化估計可等效為在幅度值為1約束條件下的線性最小化求解。但是，由于式(18)是非確定性多項式困難問題，當向量維數大時，CMQP等式的最優化求解非常困難。因此，一般采用近似估計算法求解CMQP最優解。

近年來，半正定規劃(SDP)方法成為求解CMQP等式最優化問題的熱門方法。對于CMQP最優化問題求解，SDP過程的典型表達式為：

為了求解式(20)中的SDP問題，可利用現有的凸優化算法估計求解，如共軛梯度方法、內點法等。另外，目前許多學者也開發了各種SDP求解軟件工具箱，如CVX工具箱[23]、SDPT3工具箱[24]等，可用于式(20) SDP問題的快速求解。獲得矩陣后，最優向量可通過矩陣分解得到，具體實現方法可借鑒文獻[25]，本文不再詳述。若已估，則第次迭代中壓縮感知LASAR成像模型的相位誤差估計

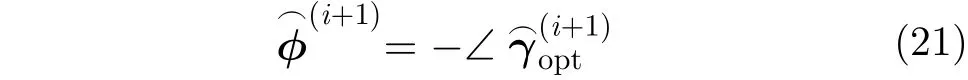
3.2 算法流程

針對LASAR稀疏自聚焦成像，根據半正定規劃自聚焦成像原理，本文SDPSA算法的主要步驟如表1所示，其主要步驟是迭代估計過程。

表1 SDPSA算法Tab. 1 SDPSA algorithm

一般情況下，SDPSA算法經過20次迭代左右可實現收斂。另外，SDPSA算法估計得到的相位誤差可能會存在線性偏移項，該誤差僅導致SDPSA自聚焦成像結果與原始圖像存在固定偏移，此時可利用定標技術或其它線性相位誤差估計方法進行補償校正，本文不再詳述。

4 實驗結果

4.1 仿真數據

為了驗證SDPSA稀疏自聚焦成像方法的性能，本節先利用LASAR仿真數據進行成像驗證，并對比基于傳統PGA相位誤差估計補償的后向投影(Back Projection， BP)算法及迭代最小二乘(IRLS)稀疏成像算法結果進行分析，分別簡稱為BP-PGA算法和IRLS-PGA算法。其中，IRLS-PGA算法是將BPPGA算法得到的相位誤差對回波數據進行補償后，再利用IRLS算法進行稀疏成像。為了簡便，該仿真實驗中只對LASAR單個等距離單元切面進行成像，實際中對全部等距離單元切面進行成像后進行合并即可得LASAR觀測場景3維成像。

仿真中假設LASAR系統采用正下視工作模式，主要仿真參數如下：雷達中心頻率為30 GHz，發射信號帶寬為 1 GHz，信號采樣率為1.2 GHz，脈沖重復頻率PRF為1200，載荷平臺飛行速度為線長度為5 m，線陣天線陣元為等間隔均勻分布，線陣天線陣元數為128，系統沿航向采樣點數為128，距離向采樣點數為1024。值得注意的是，為了便于CS測量矩陣構造及計算，仿真中線陣天線陣元間隔約為4個波長，只適用于小觀測場景成像仿真，但大場景仿真時應要求陣元間隔小于半個波長以避免柵瓣影響。仿真中原始場景存在4個單點目標，其散射系數相同。在成像處理中，等距離切面成像空間與原始場景相同，平面空間范圍為64 m×64 m，被均勻離散化成64×64個分辨單元。為了分析SDPSA算法在不同類型相位誤差情況下稀疏自聚焦性能，在仿真回波數據中分別加入緩變和陡變的相位誤差，并且在方位向-切航向平面隨機抽取50%和25%回波數據進行成像對比分析。

首先，在回波數據中加入沿航向緩變、切航跡陡變的相位誤差，其中沿航跡相位誤差在為二次項函數、切航跡相位誤差在區間上服從均勻隨機分布，脈壓后回波數據信噪比(Signal to Noise Ratio， SNR)為25 dB。圖2給出了存在相位誤差時全部回波數據、50%方位-切航隨機抽取回波數據和25%方位-切航隨機抽取回波數據情況下BP未自聚焦、BP-PGA、BP-SDPSA(即利用SDPSA算法估計得到的相位誤差對BP算法進行補償)、IRLS未自聚焦、IRLS-PGA和SDPSA算法的仿真點目標成像，其中圖像顯示經過歸一化處理且幅度取對數，圖像顯示門限為-30 dB。從圖2可知，在此相位誤差情況下BP算法和IRLS算法未自聚焦時成像失效，點目標散焦嚴重；經過PGA算法相位誤差補償后，BP和IRLS沿航跡向成像質量得到一定提升，但切航跡向成像提升不明顯，BP-PGA和IRLS-PGA結果非目標區域仍然存在大量的旁瓣或虛假目標，并且隨著回波數據利用率減少自聚焦成像性能下降。相對于PGA算法相位誤差補償，SDPSA算法在全部回波數據、50%回波數據和25%回波數據條件下均得到點目標的良好聚焦成像結果，而且非目標區域幾乎沒有旁瓣和虛假目標。另外，經過SDPSA算法相位誤差補償后，在不同回波數據情況下BP-SDPSA成像結果較BP-PGA也抑制了沿航跡向和切航跡向的旁瓣水平，提高了自聚焦成像質量。布，脈壓后回波數據SNR為25 dB。圖3給出了存在相位誤差時全部回波數據、50%回波數據和

25%回波數據情況下BP未自聚焦、BP-PGA、BPSDPSA、IRLS未自聚焦、IRLS-PGA和SDPSA算法的仿真點目標成像，其圖像顯示同圖2。從圖3可知，在此隨機相位誤差情況下PGA算法性能提升很小，尤其是非全部回波數據時BP-PGA和IRLSPGA目標散射嚴重。然而， SDPSA算法在全部回波數據、50%回波數據和25%回波數據時都實現了點目標良好聚集成像，原始場景中4個單點目標被精確恢復，并且BP-SDPSA成像結果旁瓣水平較BP-PGA也大大降低。實驗結果驗證了SDPSA算法在壓縮感知LASAR稀疏自聚焦成像的有效性，說明了該算法可對LASAR稀疏回波數據條件下緩變及陡變相位進行估計和補償。

圖2 沿航跡二次項及切航跡隨機分布相位誤差下仿真點目標成像結果(上：全部回波數據；中：50%回波數據；下：25%回波數據)Fig. 2 The results of the point targets in the case of the along-track quadratic phase errors and cross-track random phase errors(Top： all samples; Middle： 50% samples; Bottom： 25% samples)

圖3 沿航跡及切航跡隨機分布相位誤差下仿真點目標成像結果(上：全部回波數據；中：50%回波數據；下：25%回波數據)Fig. 3 The results of the point targets in the case of the along-track random phase errors and cross-track random phase errors(Top： all samples; Middle： 50% samples; Bottom： 25% samples)

最后，為了分析SDPSA算法在不同SNR及迭代次數情況下自聚焦性能，將圖2中SNR變為0至30 dB，圖4(a)給出了全部、50%和25%回波數據量時SDPSA算法成像結果與原始仿真場景的MSE。可知，SDPSA算法的MSE隨著SNR增大而變小，并且在SNR為0 dB至5 dB時MSE大于0.1，但SNR大于10 dB后MSE均小于0.1且變化很小。因此，當脈壓后回波數據SNR大于10 dB時，SDPSA算法可良好實現稀疏自聚焦成像。對于LASAR原始回波數據，通常其脈沖壓縮后回波數據SNR可優于10 dB，滿足SDPSA算法稀疏自聚焦成像要求。圖4(b)給出了回波數據SNR為20 dB，全部、50%和25%回波數據量時SDPSA算法MSE隨迭代次數變化曲線，可知全部數據成像時5次迭代后基本收斂，而在50%和25%回波數據時10次迭代后基本收斂，此時算法MSE均小于0.1。

4.2 實測數據

為了進一步驗證本文SDPSA算法的有效性，利用本課題組地基等效LASAR實驗系統獲取的實測數據進行稀疏自聚焦成像分析。地基等效LASAR實驗系統實物圖如圖5(a)所示，系統主要參數如下：雷達中心頻率為9.62 GHz，發射信號帶寬為80 MHz，信號采樣率為120 MHz，線陣長度為1.25 m。實驗場景為地面足球場并布置3個參考球目標，其光學圖像如圖5(b)和圖5(c)所示，包含了兩種目標類型：簡單的球目標和較復雜的路燈鐵柵欄，該觀測場景中心到實驗平臺的距離大約為100 m。

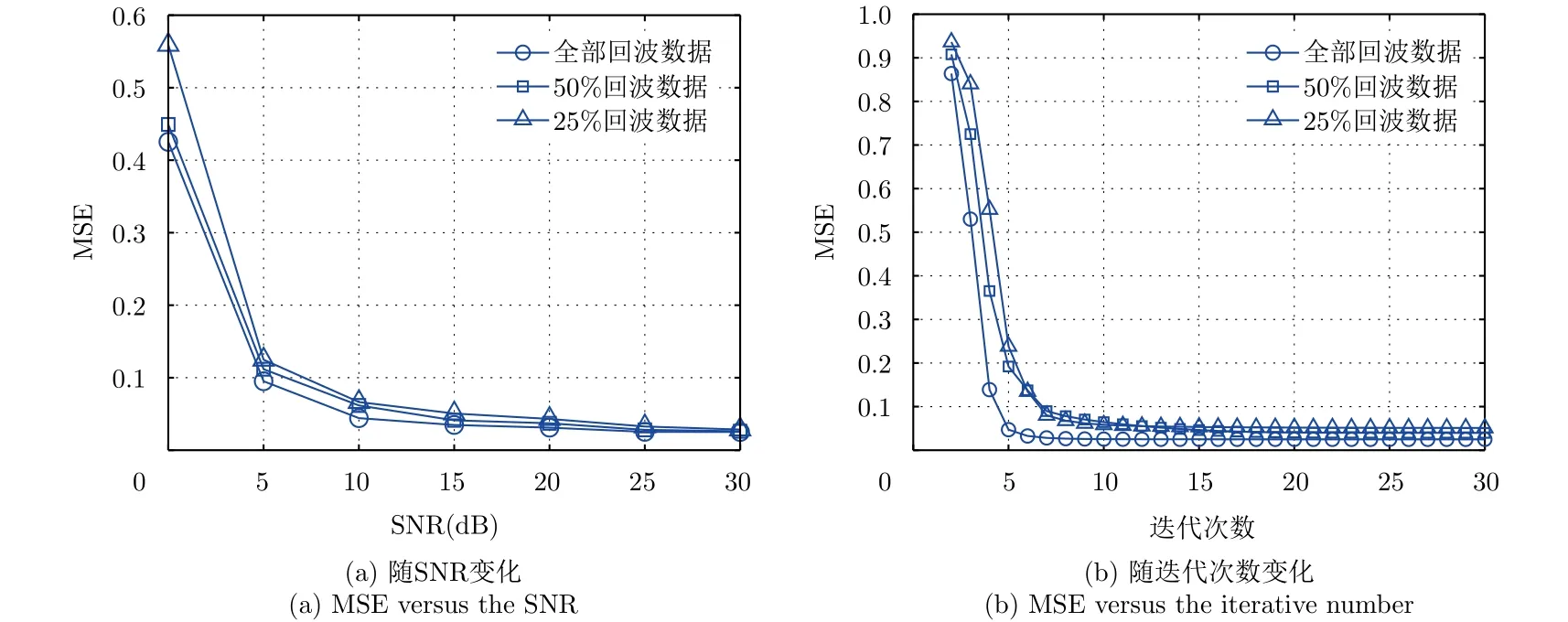
圖4 SDPSA算法MSE變化曲線Fig. 4 The MSE curve of SDPSA

圖5 地基等效LASAR成像實驗Fig. 5 The ground-based LASAR experiment

圖6 (a)給出了實驗系統天線掃描的2維軌跡，可等效為一個虛擬的2維天線陣列，此虛擬陣列大小為1.25 m×1.25 m，陣列的陣元個數為10416，此時觀測區域成像不會出現柵瓣。圖6(b)為圖6(a)對應的脈壓后回波數據，其中球1回波對應于第18個距離單元數據、球2和球3對應于第29個距離單元數據，路燈對應于第76個距離單元數據。為了分析測量陣元樣本數對壓縮感知LASAR稀疏自聚焦成像的影響，本節圖6(b)選擇個陣元的脈壓后回波數據，并以此數據作為參考的全部回波數據，然后分別從該10000樣本陣元數中隨機選擇5000和2000個陣元的回波數據作為稀疏2維陣列回波。在回波數據加入2維陣列平面相位誤差，該相位誤差在區間上服從均勻隨機分布，并對比傳統PGA算法，分析壓縮感知LASAR自聚焦成像性能。

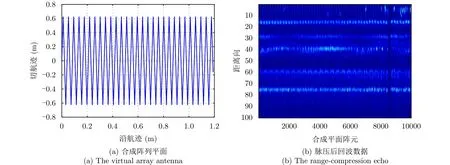
圖6 地基LASAR合成陣列平面及回波數據Fig. 6 The virtual array antenna and the echo of the ground-based LSAR

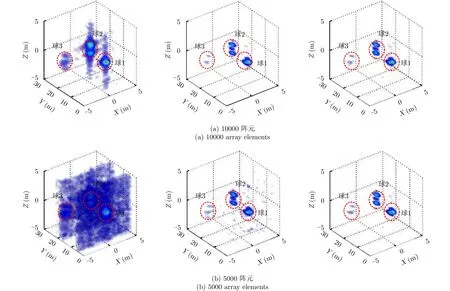
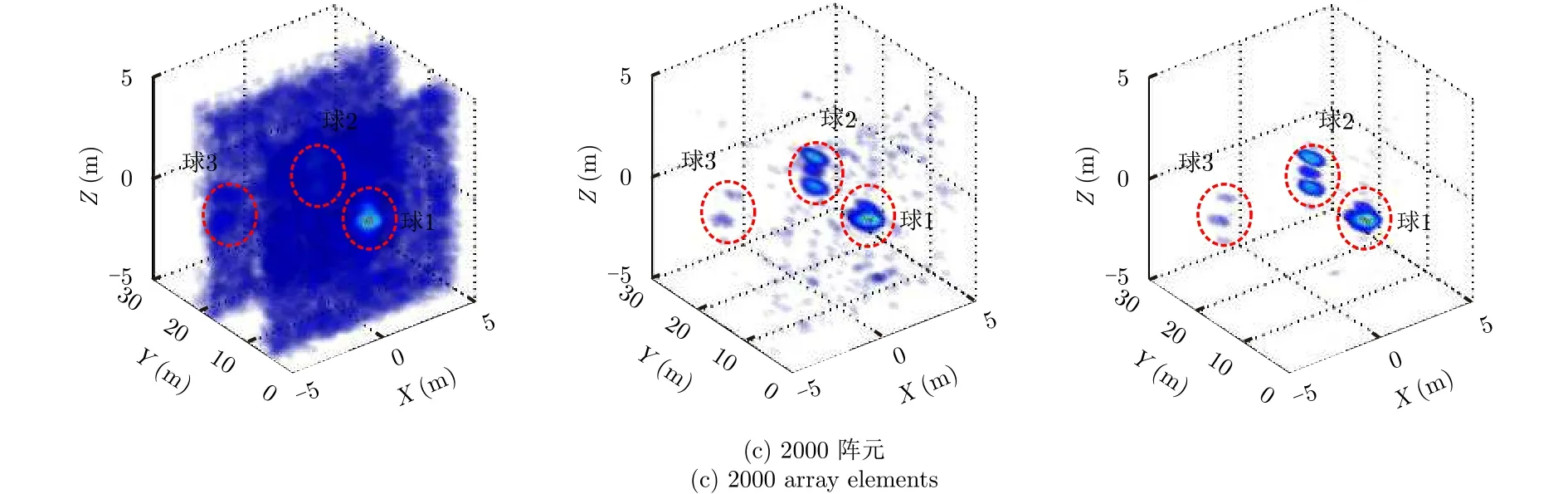
圖7 球目標實測數據稀疏自聚焦成像結果(左：BP-PGA算法；中：IRLS-PGA算法；右：SDPSA算法)Fig. 7 The sparse autofocusing results of the experimental balls data(Left： BP-PGA; Middle： IRLS-PGA; Right： SDPSA)

圖7 給出了10000， 5000和2000陣元回波數據條件下采用BP-PGA， IRLS-PGA及本文SDPSA算法獲得的實驗球目標自聚焦成像結果，其中圖像已歸一化且顯示門限為最大值-25 dB。從圖7成像結果看出，在10000個陣元回波數據時3種算法對3個參考球目標均能良好自聚焦成像，且IRLS-PGA算法和本文SDPSA算法結果相似，說明PGA算法和本文算法在10000個陣元回波數據時自聚焦性能相當。但是，在5000和2000陣元回波數據成像時，BP-PGA算法出現嚴重旁瓣干擾，3個參考球目標在X-Z平面存在很高的旁瓣串擾；IRLS-PGA算法在球體目標周圍出現虛假目標，且2000陣元樣本時結果更加惡化，說明PGA自聚焦算法在數據欠采樣時相位誤差估計精度下降，并且隨著樣本數減少自聚焦性能變差。然而，SDPSA算法在5000和2000稀疏陣元樣本時，成像結果與10000陣元基本一致，較IRLS-PGA算法結果大大抑制了虛假目標，說明SDPSA算法的相位誤差估計性能優于PGA算法，在稀疏欠采樣數據時仍可良好實現LASAR相位誤差估計和校正。

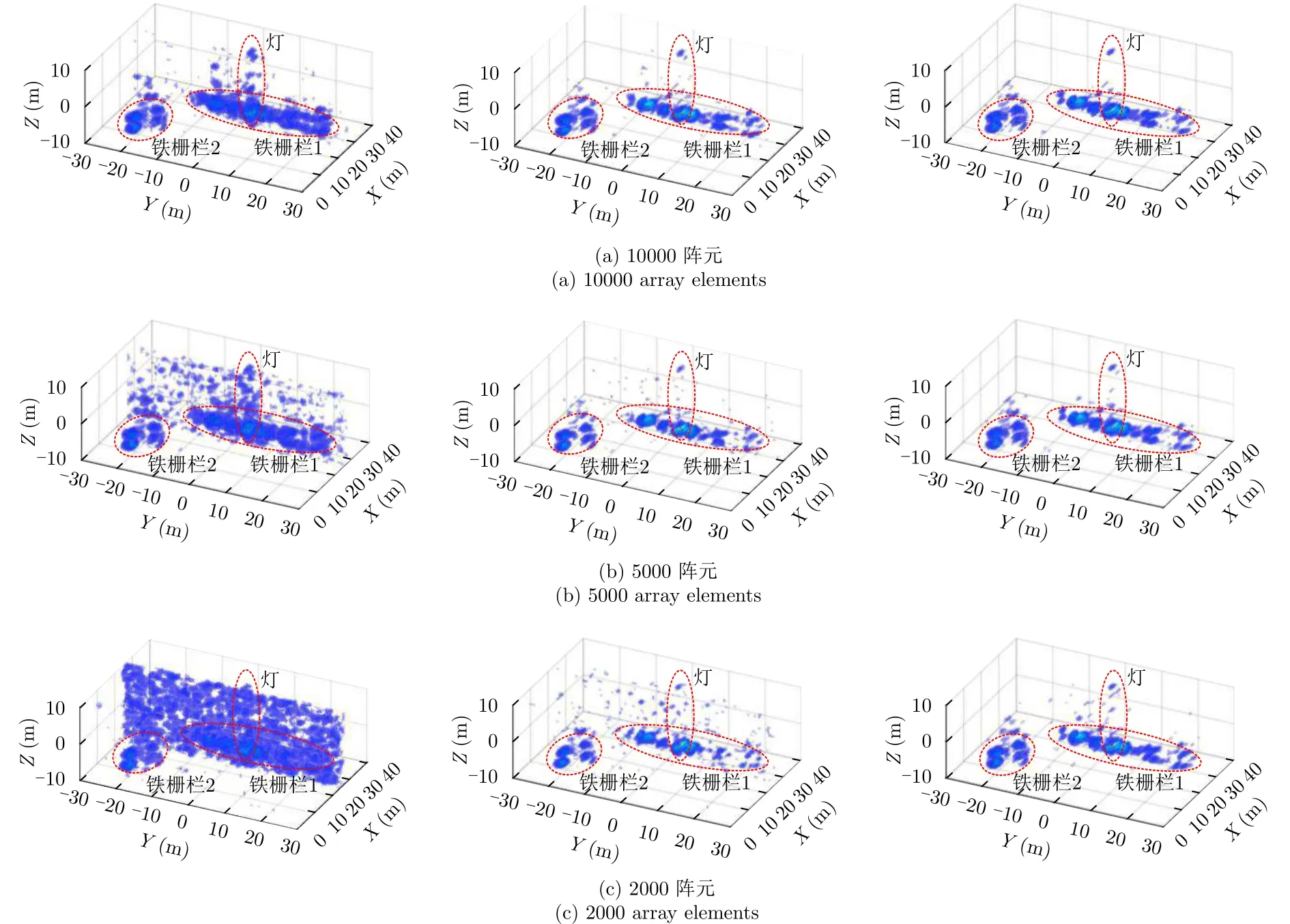
圖8 路燈目標實測數據稀疏自聚焦成像結果(左：BP-PGA算法；中：IRLS-PGA算法；右：SDPSA算法)Fig. 8 The sparse autofocusing results of the experimental light data(Left： BP-PGA; Middle： IRLS-PGA; Right： SDPSA)

圖8 給出了10000， 5000和2000陣元回波數據條件下采用BP-PGA， IRLS-PGA及本文SDPSA算法獲得的路燈鐵柵欄目標自聚焦成像結果，其中圖像已歸一化且顯示門限為最大值-20 dB。從圖8成像結果看出，相對傳統BP-PGA和IRLS-PGA算法，SDPSA算法在10000， 5000和2000陣元樣本時對路燈和鐵柵欄目標成像均有明顯提升，同樣驗證了SDPSA算法稀疏自聚焦性能優于傳統PGA算法，在稀疏陣元采樣數據時可實現LASAR相位誤差估計和校正。綜上，地基LASAR實測數據實驗結果驗證了本文SDPSA算法的有效性。

5 結論

本文提出了一種基于半正定規劃的壓縮感知LASAR自聚焦3維成像算法。該SDPSA方法結合LASAR壓縮感知成像原理及最小均方誤差準則，利用松弛半正定規劃方法及迭代最優方法估計相位誤差，實現壓縮感知LASAR的高精度自聚焦成像，并且為了進一步提高自聚焦算法運算效率，通過主散射目標區域進行相位誤差估計。仿真數據和實測數據驗證了本文SDPSA算法的有效性，實驗結果說明相對于傳統PGA自聚焦算法，SDPSA算法在稀疏采樣數據條件下具備更好的稀疏自聚焦成像結果，可為LASAR 3維成像技術實際應用提供技術途徑。在未來工作中，可開展算法優化研究，進一步提升SDPSA算法的運算效率。