基于物聯(lián)網(wǎng)的物流園區(qū)門區(qū)優(yōu)化仿真

鄭彩金，何世偉，畢明凱，陳旭超

(北京交通大學 城市交通復雜系統(tǒng)理論與技術教育部重點實驗室，北京 100044)

0　引言

物流園區(qū)是物流作業(yè)的集中地和多種運輸方式的銜接點，使得物流園區(qū)具有較大的交通量.物流園區(qū)門區(qū)作業(yè)組織優(yōu)化，可以減少車輛等待時間，提高物流園區(qū)整體作業(yè)效率，同時減少車輛的污染排放.因此，對于物流園區(qū)門區(qū)的作業(yè)組織優(yōu)化是有重要研究價值和意義的.

國內(nèi)外學者在相關方面做了大量研究，戴越[1]等對目前常規(guī)的物流園區(qū)出入口設計及其優(yōu)化進行了探討.宋曉俊[2]等在分析物流園區(qū)交通特性的基礎上，定量地分析交通量確定最佳出入口.李守林[3]研究了基于物聯(lián)網(wǎng)驅動的物流園區(qū)出入口車輛排隊系統(tǒng).歸敏丹等[4]利用排隊論知識對多服務員情況下的排隊現(xiàn)象進行分析，得出單一共享的排隊等候隊列的性能要優(yōu)于多個獨自的排隊等候隊列的結論.Matthew Fleming等[5]運用面向對象的仿真模型，在考慮車輛在隊列中移動需花費時間的基礎上，運用車輛跟馳模型，研究比較了集裝箱碼頭兩種排隊模式，得出了單隊列排隊模式優(yōu)于傳統(tǒng)排隊模式的結論.Chu Cong Minh等[6]在定量比較分析集裝箱碼頭兩種排隊模式的基礎上，開發(fā)了用于評估優(yōu)化集裝箱碼頭門區(qū)的平臺.Guan和Liu[7-8]在分析研究集裝箱碼頭兩種排隊策略的基礎上，考慮了更復雜的排隊情景，運用M/G/n排隊模型來計算最少的門區(qū)服務臺數(shù)量.

現(xiàn)有大多數(shù)研究主要針對物流園區(qū)門區(qū)布局和數(shù)量以及對門區(qū)排隊模式進行研究，且多數(shù)研究不但是基于經(jīng)驗公式的定量理論計算，也未考慮不同貨物具有不同的時間敏感性.本文基于Anylogic仿真軟件對門區(qū)作業(yè)進行仿真，對比分析門區(qū)兩種排隊模式優(yōu)缺點，基于物聯(lián)網(wǎng)技術，按照不同貨物的時間敏感性劃分貨物優(yōu)先級，根據(jù)優(yōu)先級先后進行作業(yè)，確保不同等級貨物的運輸時效性，提高物流園區(qū)整體作業(yè)效率.

1　問題描述

物流園區(qū)具有較大的交通需求，然而物流園區(qū)門區(qū)是產(chǎn)生運輸延遲的主要區(qū)域之一.車輛在物流園區(qū)門區(qū)作業(yè)時，部分隊列前方車輛作業(yè)時間較長，該隊列后方所有車輛都需排隊等待，導致部分車輛排隊等待時間過長，尤其在車輛到達高峰期，門區(qū)排隊隊長增加，車輛排隊等待時間延長.同時，未考慮不同貨物具有不同的運輸剩余時間及時間敏感性，對于運輸剩余時間少、時間敏感度高的貨物沒有采取合理有效的作業(yè)組織優(yōu)化措施，使園區(qū)服務水平大大降低.另外，由于沒有針對性的作業(yè)組織優(yōu)化，貨物在門區(qū)作業(yè)時間大大超過其預期作業(yè)時間，使得后續(xù)物流作業(yè)不能順利進行，降低了物流園區(qū)整體作業(yè)效率.

2　多種排隊模式對比分析

(1)先到先服務排隊模式：先到先服務，即按照到達次序服務.

①多隊列排隊模式

在多隊列排隊系統(tǒng)中，若車輛到達服從泊松分布過程，服務時間相互獨立且服從相同的負指數(shù)分布，同時車輛到達間隔時間和服務時間是相互獨立的，此時可以使用標準的M/M/1模型，如圖1所示.設車輛到達規(guī)律服從參數(shù)為λ的泊松過程，服務時間服從參數(shù)為μ的負指數(shù)分布，門區(qū)服務臺數(shù)量為n，則每個服務臺的車輛到達規(guī)律服從參數(shù)為λ/n的泊松過程.其中，服務強度(服務臺平均利用率)ρ=λ/(nμ)<1.

車輛的平均等待時間為：

(1)

隊列的平均隊長為：

(2)

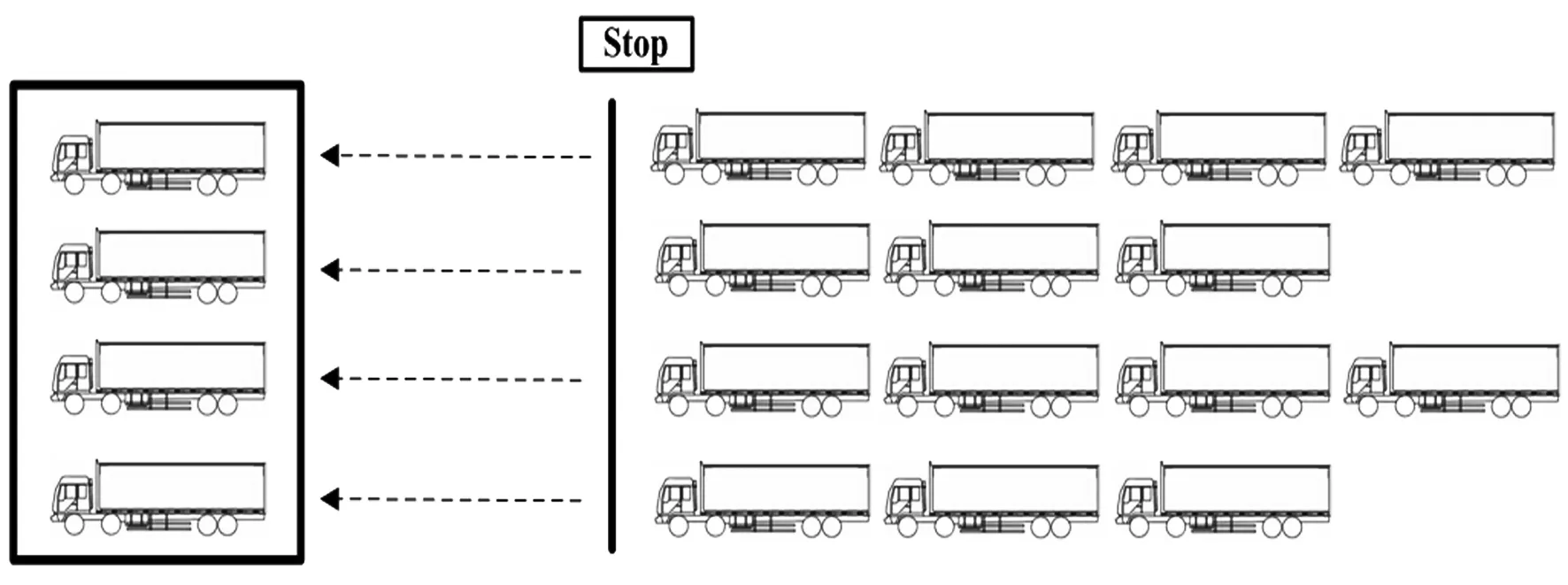
圖1　多隊列排隊模式示意圖

②單隊列排隊模式

在單隊列排隊系統(tǒng)中，若車輛到達、服務條件同①，可以使用標準的M/M/c模型，如圖2所示.其中，服務強度(服務臺平均利用率)ρ=λ/(nμ)<1.

車輛的平均等待時間為：

(3)

隊列的平均隊長為

(4)

圖2　單隊列排隊模式示意圖

(2)有優(yōu)先權的服務模式

基于物聯(lián)網(wǎng)的物流園區(qū)門區(qū)服務模式屬于有優(yōu)先權的服務模式.基于物聯(lián)網(wǎng)技術，可根據(jù)車輛裝載貨物的運輸剩余時間和時間敏感度將其劃分為不同優(yōu)先級，劃分方法如表1所示.

表1　車輛門區(qū)作業(yè)優(yōu)先級劃分

在該服務模式中，優(yōu)先級高的車輛先作業(yè)，優(yōu)先級相同的車輛先到先作業(yè)，如當優(yōu)先級為一級車輛均作業(yè)完畢時，優(yōu)先級為二級的車輛方可開始作業(yè)，以此類推，實現(xiàn)按優(yōu)先級作業(yè)的門區(qū)作業(yè)組織.

3　構建仿真數(shù)學模型

大多數(shù)物流園區(qū)門區(qū)均采用多隊列排隊模式.該模式下的n個服務臺對應了n個隊列，該排隊模式下，一旦某車輛作業(yè)遇到問題，該車輛所在隊列后方車輛均需等待.單隊列排隊模式就可以避免這個問題的產(chǎn)生，該模式下的n個服務臺對應了一個共享隊列，該排隊模式下，某車輛作業(yè)遇到問題并不會直接影響后方車輛作業(yè)，而且會在真正意義上實現(xiàn)FCFS(First Come First Served).

在確定物流園區(qū)門區(qū)服務臺數(shù)量時，需同時考慮車輛的平均等待時間和門區(qū)的運營成本.在確定λ和μ的情景下，通過給定等待時間閾值(最小平均等待時間)T來確定最優(yōu)服務臺數(shù)n*，T越小則n*越大.

兩種不同排隊模式下的門區(qū)服務臺數(shù)確定方法分別為：

①多隊列排隊模式

多隊列排隊模式的n*的確定，可以通過經(jīng)典M/M/1模型推導得出：

(5)

λ,μ,ρ,T>0

(6)

滿足上述不等式的最小整數(shù)解n，即為最優(yōu)解n*.

②單隊列排隊模式

單隊列排隊模式的n*的確定，可以利用M/M/c模型解決：

minn

(7)

(8)

λ,μ,ρ,T>0

(9)

由于n為正整數(shù)，可通過將n由低到高代入上述不等式計算，滿足上述不等式的最小值n，即為最優(yōu)解n*.

4　案例分析

某物流園區(qū)門區(qū)車輛到達服從泊松過程，平均到達率λ=1.5 輛/min，門區(qū)服務時間服從負指數(shù)分布，平均服務率μ=0.192 3 輛/min，車輛到達間隔時間和服務時間相互獨立.在不超過給定的平均排隊等待時間閾值的基礎上，確定門區(qū)服務臺數(shù)量，平均排隊等待時間閾值由5～30 min依次遞增，每次遞增5 min.首先在不考慮優(yōu)先級的情況下，對比分析單隊列排隊模式和多隊列排隊模式，主要從基于某等待時間閾值的最優(yōu)服務臺數(shù)量、其所對應的平均排隊時間、平均隊長等幾個方面來對比分析，選取較優(yōu)的排隊模式應用于考慮優(yōu)先級的門區(qū)作業(yè)組織.其次，應用較優(yōu)排隊模式，考慮運輸優(yōu)先級，對比分析不同優(yōu)先級所占比例改變對門區(qū)作業(yè)的影響，同時，與未考慮運輸優(yōu)先級作業(yè)進行對比分析.

使用Anylogic仿真軟件，對該物流園區(qū)門區(qū)作業(yè)進行仿真.設定仿真時間為30 d，即43200min.仿真完成時，輸出隊列平均隊長、平均等待時間和平均逗留時間等數(shù)據(jù).如圖3所示.

圖3　基于Anylogic的物流園區(qū)門區(qū)作業(yè)仿真

(1)未考慮貨物運輸優(yōu)先級情景下物流中心門區(qū)仿真分析

具體輸入相關數(shù)據(jù)進行仿真，得到不考慮優(yōu)先級結果如表2所示.

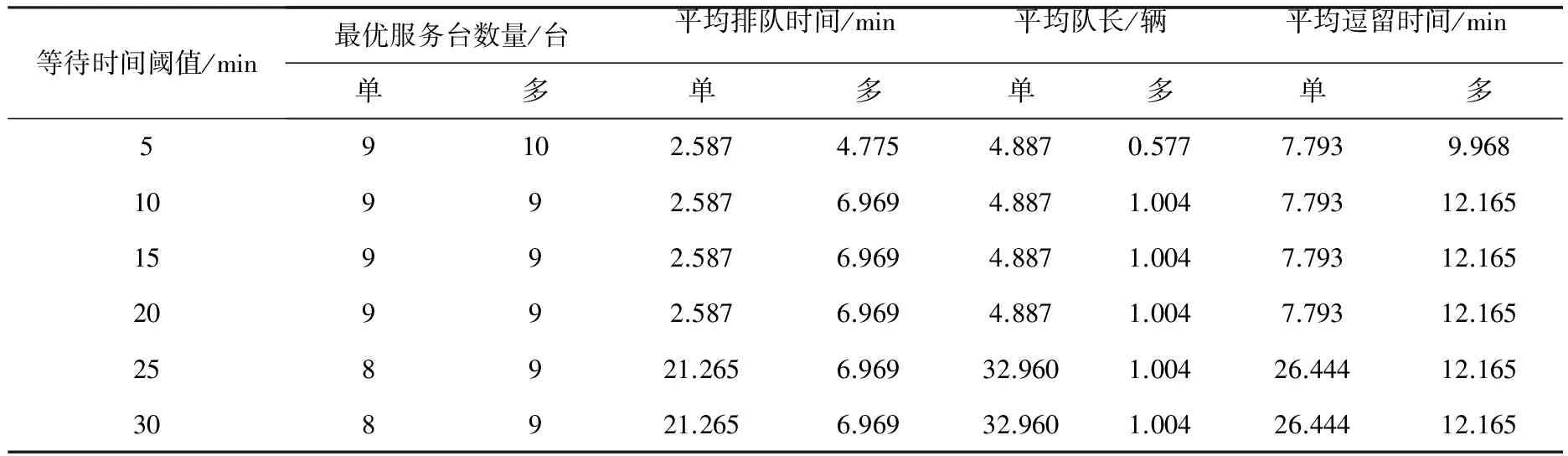
表2　基于不同時間閾值和不同排隊模式的門區(qū)服務臺數(shù)對比分析

注：單—單隊列排隊模式，多—多隊列排隊模式

如表1所示，同一等待時間閾值下，單隊列排隊模式下的最優(yōu)服務臺數(shù)不超過多隊列排隊模式的，最優(yōu)服務臺數(shù)相同時，單隊列排隊模式下的平均排隊時間較少，因此采用單隊列排隊模式能夠有效降低物流園區(qū)門區(qū)的運營成本和運輸成本.但單隊列排隊模式下的平均隊長較對多列排隊模式要長，在物流園區(qū)沒有足夠空間來容納一個長隊列時，可以將隊列拆分成若干個較短隊列，如圖4所示.

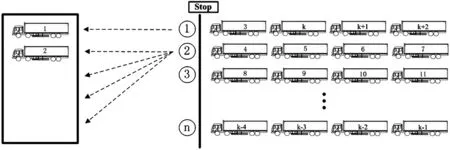
圖4　單隊列排隊模式拆分排隊策略

如圖4所示，車輛按照到達順序編號排隊，當?shù)谝粋€隊列排滿時，轉至下一個空隊列排隊，當最后一個隊列滿時，轉至第一個隊列.這種排隊策略嚴格實現(xiàn)了FCFS的排隊原則.

①車輛到達率和等候時間閾值對門區(qū)最優(yōu)服務臺數(shù)的影響.分析研究車輛到達率和等候時間閾值對門區(qū)最優(yōu)服務臺數(shù)的影響，假定門區(qū)服務時間服從負指數(shù)分布，平均服務率每分鐘μ=0.1923輛，車輛到達服從泊松過程，對比分析每分鐘平均到達率從λ=0.1～1.9變化對門區(qū)最優(yōu)服務臺數(shù)的影響.如表3所示.

表3　車輛到達率和平均等候時間閾值對門區(qū)服務臺數(shù)影響

如表3所示，當λ<0.3時，兩種排隊模式下的最優(yōu)服務臺數(shù)相同，但當λ較大T較小時，兩種排隊模式的差異較為明顯，反之差異較小.同一約束條件下，單隊列排隊模式的門區(qū)服務臺數(shù)需求均不大于多隊列排隊模式.

②平均服務率和等候時間閾值對門區(qū)最優(yōu)服務臺數(shù)的影響.分析研究平均服務率和等候時間閾值對門區(qū)最優(yōu)服務臺數(shù)的影響，假定車輛到達服從泊松過程，平均到達率每分鐘λ=1.5輛，門區(qū)服務時間服從負指數(shù)分布，對比分析每分鐘平均服務率從μ=0.140～0.240變化對門區(qū)最優(yōu)服務臺數(shù)的影響.如表4所示.

表4平均服務率和平均等候時間閾值對門區(qū)服務臺數(shù)影響

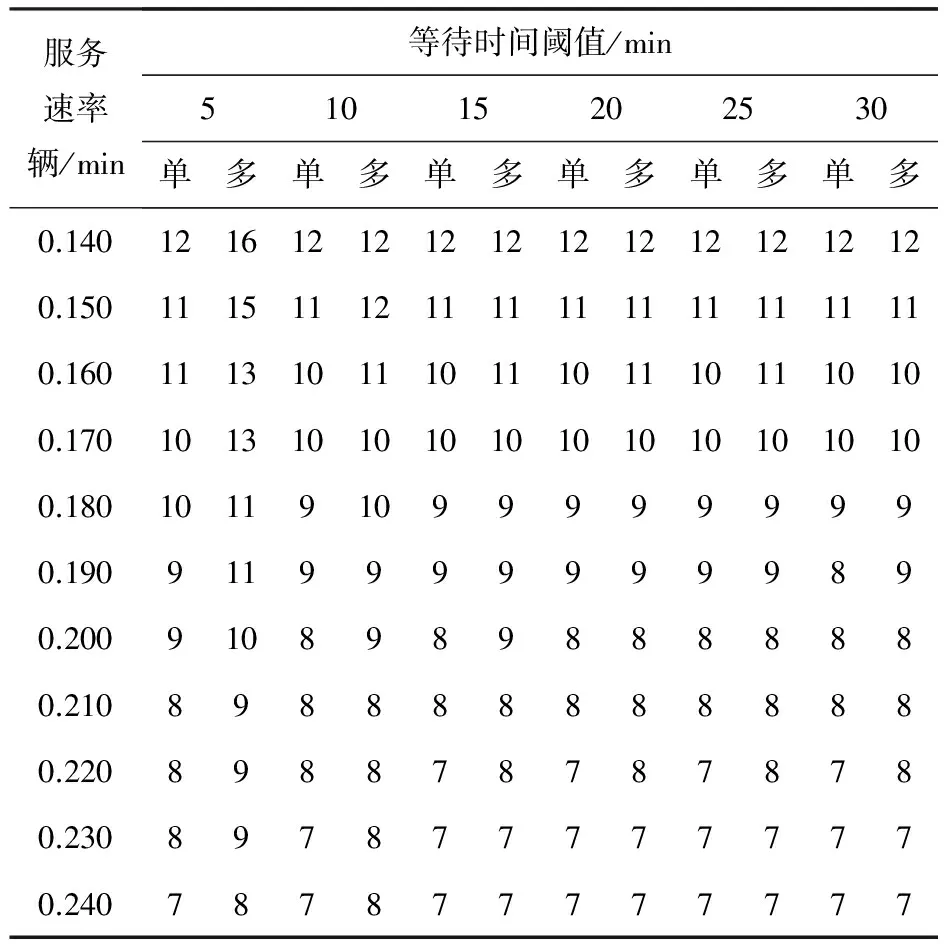
服務速率輛/min等待時間閾值/min51015202530單多單多單多單多單多單多0．1401216121212121212121212120．1501115111211111111111111110．1601113101110111011101110100．1701013101010101010101010100．1801011910999999990．19091199999999890．20091089898888880．2108988888888880．2208988787878780．2308978777777770．240787877777777

如表4所示，當μ和T較小時，兩種排隊模式的差異較為明顯，反之差異較小.同一約束條件下，單隊列排隊模式的門區(qū)服務臺數(shù)需求均不大于多隊列排隊模式.

對比分析可得，單隊列排隊模式優(yōu)于多隊列排隊模式.同時，由于多隊列排隊模式不易于調整車輛前后順序，只能通過設置額外的通道實現(xiàn)基于運輸優(yōu)先級的門區(qū)作業(yè)，運營成本高.因此，本文選用單隊列排隊模式，進行基于貨物運輸優(yōu)先級的門區(qū)作業(yè)仿真.

(2)考慮貨物運輸優(yōu)先級的物流園區(qū)門區(qū)仿真分析

采用單隊列排隊模式，實現(xiàn)基于優(yōu)先級的門區(qū)作業(yè)的排隊策略，如圖5所示.

圖5　基于物聯(lián)網(wǎng)的高優(yōu)先級車輛優(yōu)先作業(yè)排隊策略

如圖5所示，車輛按照到達順序編號排隊，其中①②③④分別代表排列優(yōu)先級為一二三四級車輛的隊列.不同等級車輛按照其優(yōu)先級進入相應的隊列排隊等候服務，高等級隊列的車輛優(yōu)先服務，當高等級隊列為空時，低等級隊列的車輛開始作業(yè).如，當①②③隊列均為空時，處于④隊列的車輛開始作業(yè).實現(xiàn)了高優(yōu)先級車輛優(yōu)先作業(yè)，同等級車輛先到先作業(yè).

車輛到達服從泊松分布過程，服務時間相互獨立且服從相同的負指數(shù)分布，仿真過程中優(yōu)先級車輛排序為時時排序.按照實際情況設定不同優(yōu)先級車輛所占比例，仿真過程中，比例會時時波動，在最后仿真結束時，各優(yōu)先級車輛占總車輛比例與設定的比例保持一致.

根據(jù)表1所得結果，可選取8或9個服務臺.本文首先選取8個服務臺，對比分析不同優(yōu)先級所占比例不同時，對其平均等待時間、平均隊長的影響；其次，分別分析門區(qū)服務臺數(shù)分別為8個和9個的情況下，比較基于運輸優(yōu)先級作業(yè)和不基于物聯(lián)網(wǎng)的變化.輸入相關數(shù)據(jù)進行仿真，得到結果分別如表5和表6所示.

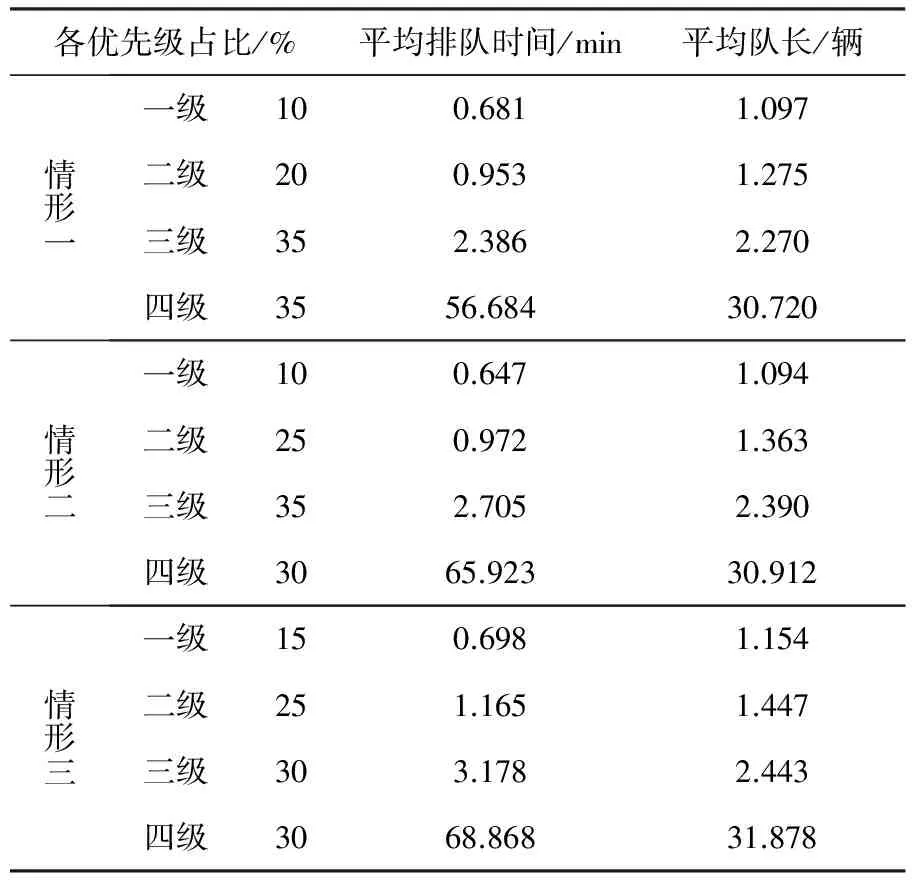
表5　各優(yōu)先級不同占比對門區(qū)作業(yè)影響對比分析

如表5所示，相同的比例變化，等級越高的比例變化所引起的相應指標的變化量越小，反之，等級越低的比例變化所引起的相應指標的變化量越大.因此，各物流園區(qū)在確認運輸優(yōu)先級劃分時，應充分考慮各等級貨運量所占比例，低等級貨物比例不能過低.

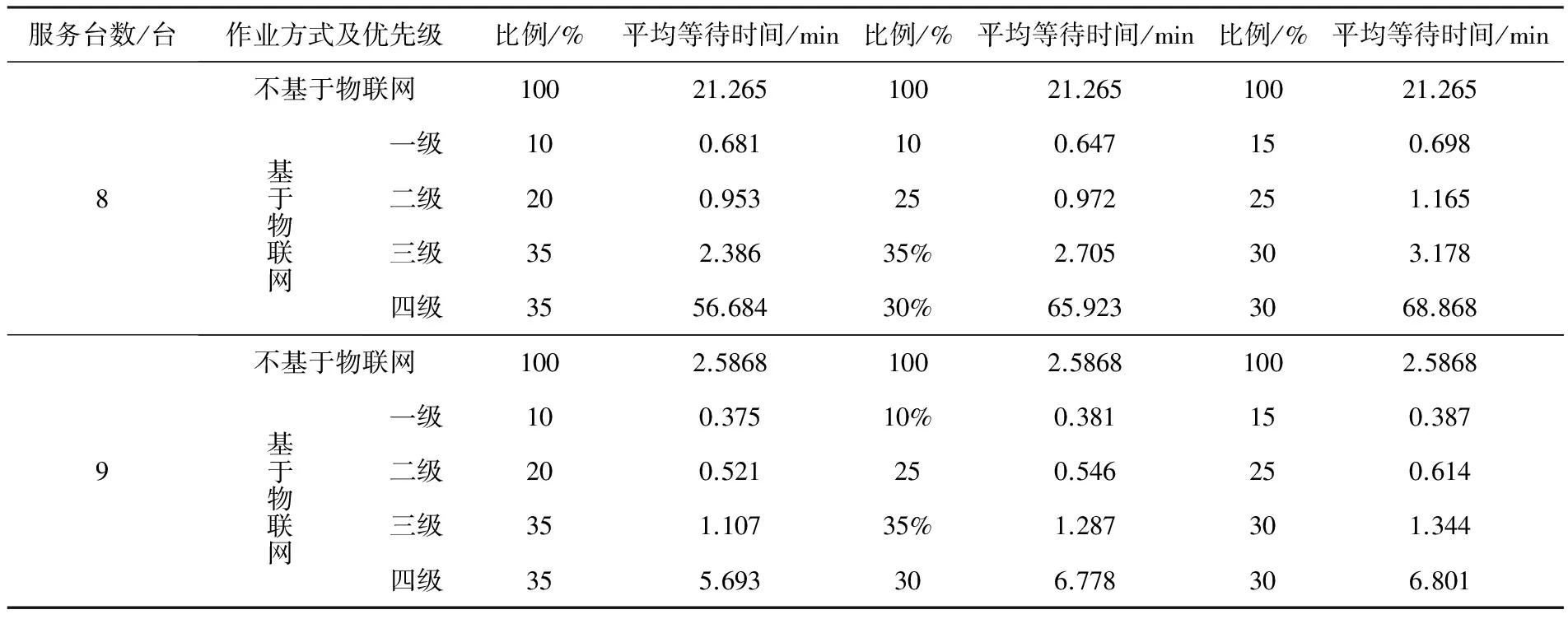
表6　基于物聯(lián)網(wǎng)作業(yè)和不基于物聯(lián)網(wǎng)對比分析

如表6所示，優(yōu)先等級越高，平均等待時間越少.其中，情景一中，門區(qū)服務臺數(shù)為8個時，基于物聯(lián)網(wǎng)作業(yè)的優(yōu)先級為一級的車輛的平均等待時間比不基于物聯(lián)網(wǎng)的縮短了近34倍，二級較之縮短了近23倍，三級縮短了近8倍.采用運輸優(yōu)先級作業(yè)的效率提升越多.但是，在提高高優(yōu)先級車輛作業(yè)效率的同時，降低了優(yōu)先級為四級的車輛的作業(yè)效率，四級車輛的平均等待時間延長了一倍左右.然而，優(yōu)先級為四級的車輛所載貨物對時間較為不敏感，因此增加一倍等待時間對其影響不大.計算可得，基于物聯(lián)網(wǎng)作業(yè)的所有車輛的平均等待時間與不基于物聯(lián)網(wǎng)作業(yè)的平均等待時間相同.因此，基于物聯(lián)網(wǎng)作業(yè)在未降低門區(qū)整體作業(yè)效率的基礎上，提高了門區(qū)作業(yè)的服務水平和效益.

5　結論

在對比分析物流園區(qū)門區(qū)單隊列排隊模式和多隊列排隊模式作業(yè)特點的基礎上，得到在多數(shù)情況下單隊列排隊模式對門區(qū)服務臺數(shù)需求更小，可以在一定程度上減少門區(qū)運營成本和運輸成本，同時針對單排隊模式存在的占地廣的問題，給出了相應的排隊策略.繼而基于物聯(lián)網(wǎng)，根據(jù)車輛所裝載貨物的運輸剩余時間和時間敏感性對其進行了優(yōu)先級劃分，采用單隊列排隊模式，提出了基于物聯(lián)網(wǎng)的門區(qū)作業(yè)排隊策略，通過仿真得到，基于物聯(lián)網(wǎng)優(yōu)先級作業(yè)的一級車輛平均等待時間較不基于物聯(lián)網(wǎng)最多可縮短34倍，且在能力緊張的物流園區(qū)門區(qū)應用效果更為明顯，但在整體上未影響門區(qū)的作業(yè)效率.因此，基于物聯(lián)網(wǎng)的物流園區(qū)門區(qū)作業(yè)，可在一定程度上保障貨物運到期限，提高貨物的準時送達率，提高物流效率和供應鏈可靠性，降低物流成本.

參考文獻:

[1]戴越, 鄭宏富. 物流園區(qū)出入口規(guī)劃設計及其優(yōu)化[J]. 中國工程咨詢, 2017(3):47- 49.

[2]宋曉俊, 毛海軍. 物流園區(qū)出入口設計優(yōu)化[J]. 物流技術, 2009, 28(11):92-94.

[3]李守林. 基于物聯(lián)網(wǎng)驅動的物流園區(qū)信息化研究[D]. 北京:北京交通大學, 2016.

[4]歸敏丹, 蔣毅飛, 張志敏,等. 多服務員時兩種等待隊列性能的比較[J]. 計算機工程與應用, 2008, 44(13):44- 46.

[5]FLEMING M, HUYNH N, XIE Y. An Agent-Based Simulation Tool for Evaluating Pooled Queue Performance at Marine Container Terminals[C]. Transportation Research Record Journal of the Transportation Research Board,2013:103-112.

[6]CONG C, HUYNH N. Planning-Level Tool for Assessing and Optimizing Gate Layout for Marine Container Terminals[C]. Transportation Research Record Journal of the Transportation Research Board,2014:31-39.

[7]GUAN C, LIU R. Container terminal gate appointment system optimization[J]. Maritime Economics & Logistics, 2009, 11(4):378-398.

[8]GUAN C, LIU R. Modeling Gate Congestion of Marine Container Terminals, Truck Waiting Cost, and Optimization[C]. Transportation Research Record: Journal of the Transportation Research Board;2009:58- 67.