基于能量法的單相無刷直流電動機齒槽轉矩研究

袁子聰，彭穎卿，王 孟，尹華杰

(1.華南理工大學，廣州 510640；2 廣東美的環境電器制造有限公司，中山 528425)

0 引 言

單相無刷直流電動機(以下簡稱SPBLDCM)比三相無刷直流電動機成本低，比單相感應電動機效率高[1]，廣泛應用于風機、水泵、光盤驅動等小功率場合。但定子齒對稱的SPBLDCM沒有起動轉矩，為成功起動，需采用非均勻氣隙結構或增加輔助磁極，以使轉子在起動時定位于電磁轉矩非零的區域。輔助磁極的結構因成本高、制造復雜而較少采用，非均勻氣隙結構則會導致齒槽轉矩大和反電動勢波形畸變大，加劇轉矩脈動和噪聲等問題。

為減小非均勻氣隙SPBLDCM的轉矩脈動，國內外學者基于有限元法分析了多種SPBLDCM優化結構和措施。文獻[2]對常用的4種非均勻氣隙結構進行了分析，發現無論是平行或徑向充磁、方波激勵或正弦波激勵，采用漸變氣隙結構均可使齒槽轉矩峰值最小且轉矩曲線更平滑。文獻[3]提出了一種均勻與非均勻氣隙相結合的結構，總氣隙長度比常規非均勻氣隙小，可更有效減小齒槽轉矩和轉矩脈動,提高效率。文獻[4]提出了一種薄端傾斜的漸變氣隙結構以提高電機起動轉矩和減小脈動。文獻[5]提出在定子齒表面開不對稱的凹槽，以調整齒槽轉矩各次諧波的相位，以達到疊加后峰值被削弱的效果。文獻[6]研究發現定子齒寬與永磁體極弧長之間存在最優比例，可保持反電動勢波形為梯形，同時使齒槽轉矩峰值和轉矩脈動最小。這些基于有限元法的SPBLDCM研究存在耗時長、分析精度受網格剖分影響大、不易發現規律性等缺點[3-7]。

能量法是一種廣泛應用在三相無刷直流電動機齒槽轉矩分析的解析法，可快速求解結果且物理意義明確。人們基于其提出了三相無刷直流電動機齒槽轉矩削弱的多種方法：極槽數配合、斜槽或斜極結構[8]、極弧系數優化[9]、轉子永磁體分塊[10]、不等定子齒寬[11]等。但建立在三相無刷直流電動機基礎上的齒槽轉矩解析計算模型不適用于不對稱定子齒的情況，因而不能用于SPBLDCM的齒槽轉矩分析。

1 基于能量法的齒槽轉矩表達式

1.1 非均勻氣隙結構的齒槽轉矩表達式

為簡化分析，作如下假設：

(1) 電機定、轉子鐵心的磁導率為無窮大，即μFe=∞；

(2) 永磁體磁導率與空氣磁導率相等，即μr=1；

(3) 電機為徑向充磁、表貼式內轉子的SPBLDCM。

設α為某定子槽口中心線和某永磁磁極中心線之間的夾角，它是定、轉子間的相對位置角；θ為轉子表面的坐標角度，θ=0位于磁極的中心線。如圖1所示。

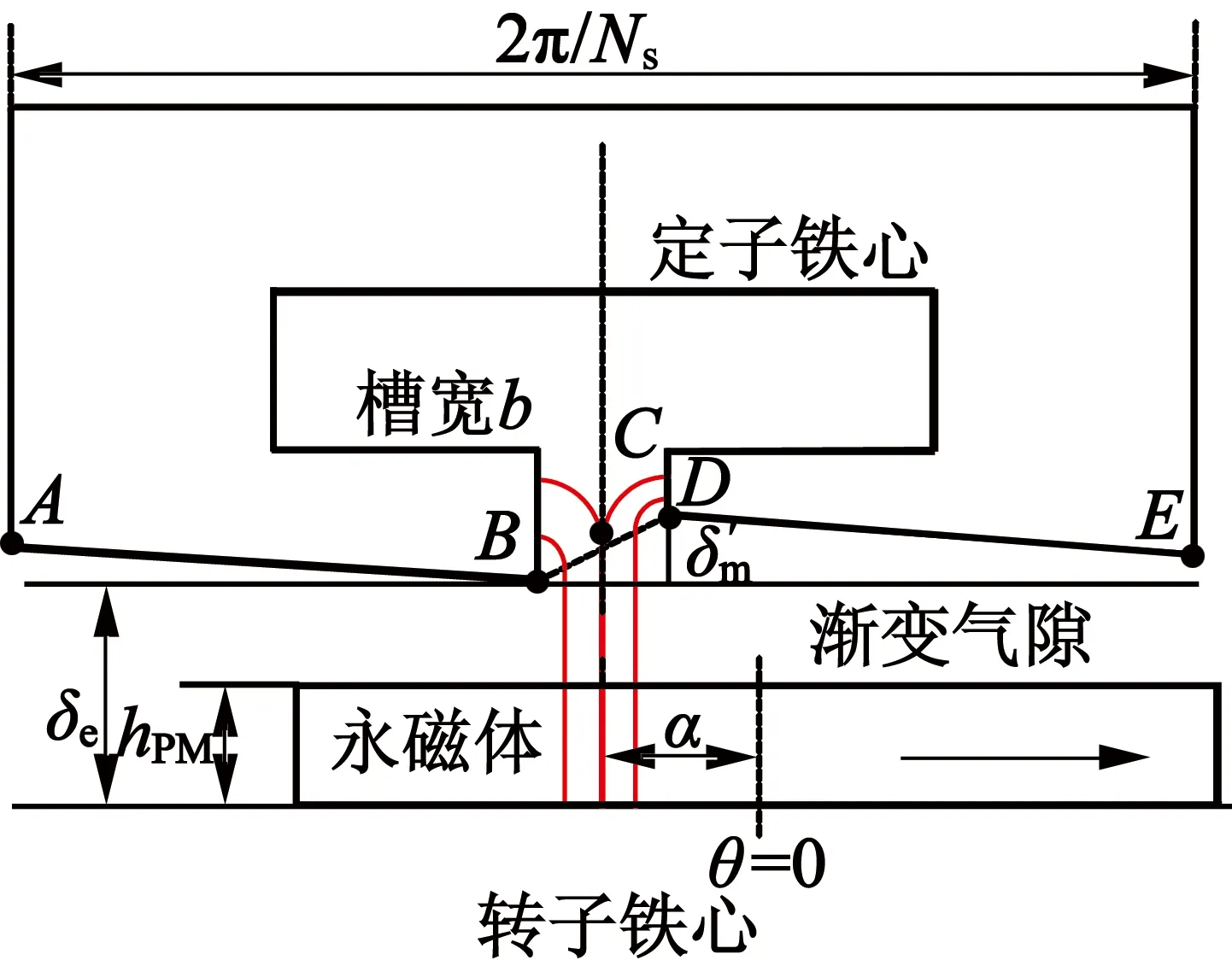
圖1永磁體與電樞的相對位置

基于能量法，齒槽轉矩可表示為電機內磁場能量W對位置角α的導數。即:

根據假設式(1)，電機的磁場能量主要存在于氣隙和永磁體內，即：

W(α)≈Wairgap+PM(α)=

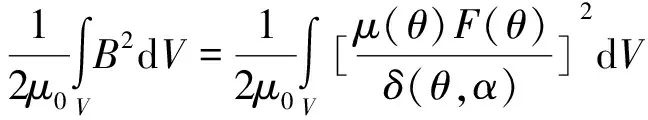
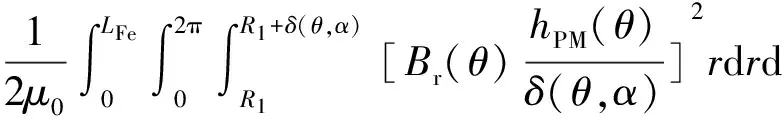
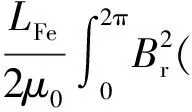
(2)

式中：Br(θ)，hPM(θ)，δ(θ,α)=δ(θ+α)分別為永磁體剩磁、充磁方向長度、有效氣隙長度等沿圓周的分布；LFe為鐵心軸向長度；R1為轉子鐵心半徑。

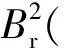
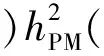
(3)

設δ′(θ,α)=δ′(θ+α)為氣隙長度中變化的部分沿圓周的分布，即δ(θ,α)=δ′(θ,α)+δe(見圖1)，則:

(4)

設定子槽數為Ns，考慮到δ′(θ,α)δe?1，則需先對G(θ,α)=G(θ+α)作泰勒展開，再在區間θ+α∈[-πNs,πNs]進行傅里葉展開：

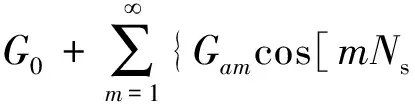
Gbmsin[mNs(θ+α)]}

(5)

由于Np=Ns，將式(3)、式(5)代入式(2)，可得:

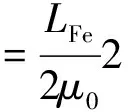
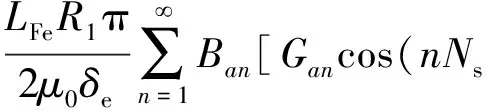
(6)

將式(6)代入式(1)，得非均勻氣隙SPBLDCM的齒槽轉矩解析表達式：

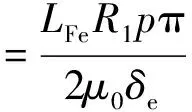
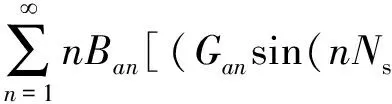
Gbncos(nNsα)]

(7)

針對漸變氣隙結構求解式(7)的傅里葉系數Ban，Gan和Gbn，即可求得相應的齒槽轉矩解析式。

1.2 等厚、均布永磁體的傅里葉系數Ban

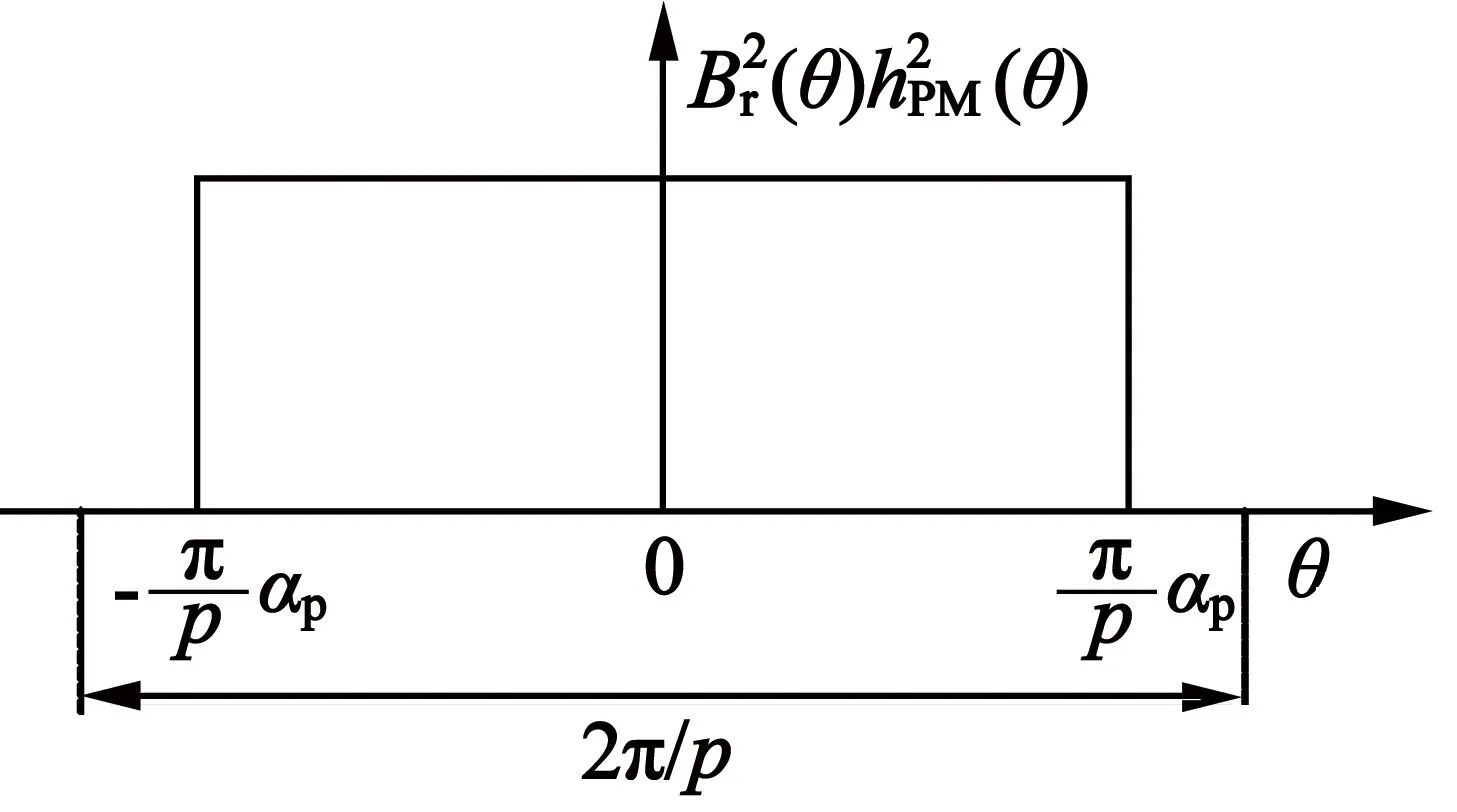
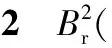
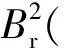
αpπ)

(8)

式中:αp為永磁體的極弧系數。

1.3 漸變氣隙的傅里葉系數Gan和Gbn

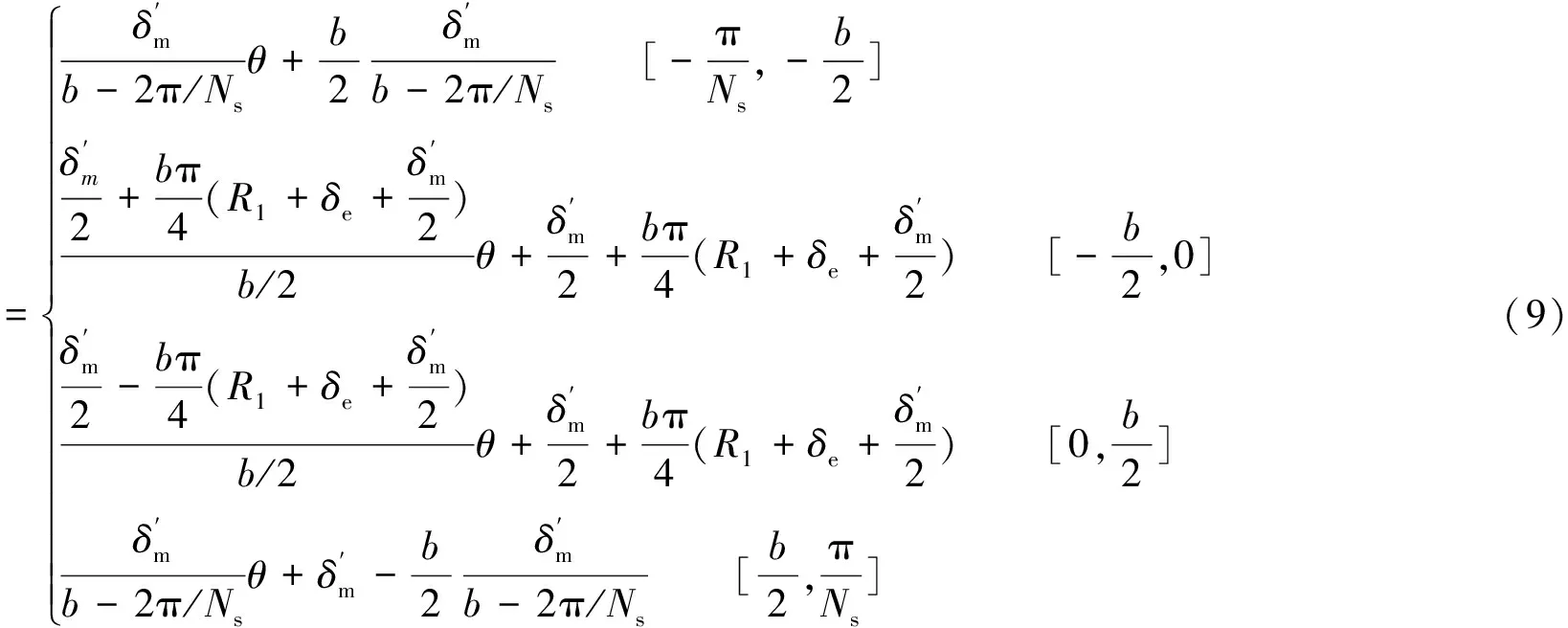
式中：b為槽口寬。

δ′(θ)波形如圖3所示。

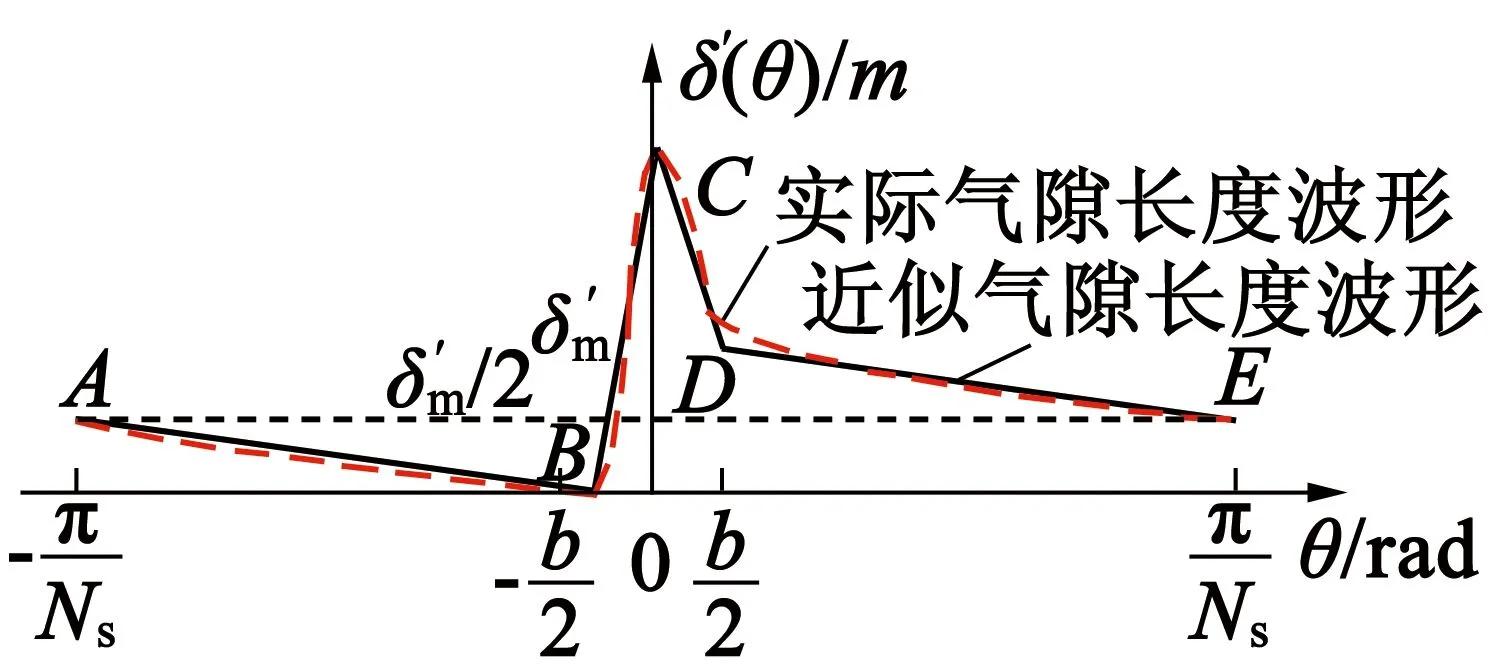
圖3近似后氣隙長度波形

基于式(9)，可求得G(θ, 0)的各次傅里葉系數：

θ)dθ=

將式(8)、式(10)、式(11)代入式(7)，可得漸變氣隙情況下SPBLDCM的齒槽轉矩表達式：

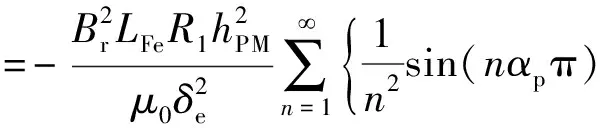
由式(12)可知：

(1) 通過對Br，LFe，R1，hPM，b和δe等參數的恰當取值，可對齒槽轉矩的幅值進行優化；

(2) 三相無刷直流電動機可以采用極、槽數的配合來提高齒槽轉矩的最低次數，削弱其幅值。但是，SPBLDCM通常設計成Ns=p，所以無法采用極、槽數配合的方法；

(3) 三相無刷直流電動機由于極槽配合的原因，齒槽轉矩的次數較高，且多數諧波都不存在，但SPBLDCM的Ns=p，齒槽轉矩的各次諧波都存在，所以常規的削弱方法作用有限，幅值更大。

2 有限元驗證

為驗證上述SPBLDCM齒槽轉矩解析模型的正確性，分別采用有限元法和能量法分析漸變氣隙對齒槽轉矩的影響，對比分析兩種方法所得結果的一致性。電機模型參數如表1所示。

表1電機模型參數

參數數值參數數值轉子極數p4永磁體剩磁Br/T0．33定子槽數Ns4槽口寬b/rad0．038378轉子外徑R1/mm12．5永磁體的極弧系數αp0．889永磁體充磁方向長度hPM/mm7．5氣隙最小長度(定、轉子鐵心間)δe/mm8鐵心疊厚LFe/mm14

2.1 SPBLDCM有限元模型

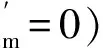
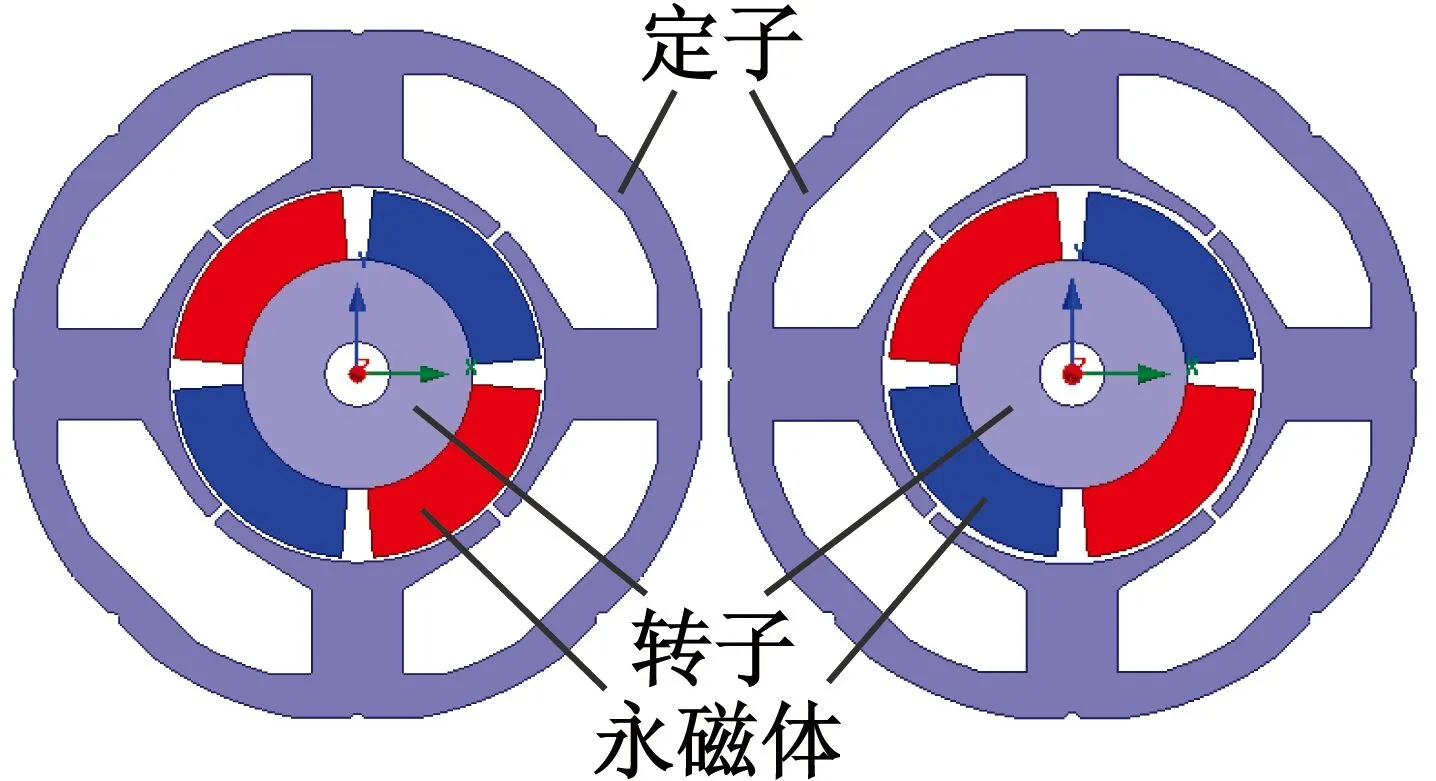
(a) 均勻氣隙 (b) 漸變氣隙

圖4SPBLDCM有限元模型

如圖5所示，F，G，H，I依次為漸變氣隙結構下的齒槽轉矩過零點、峰值點和均勻氣隙結構下的齒槽轉矩過零點、峰值點。由圖5可知，當SPBLDCM采用均勻氣隙時，齒槽轉矩將使轉子永磁體軸線與定子齒中心線對齊，齒槽轉矩過零點在α=45°的位置。而漸變氣隙則會使過零點偏離45°位置，記該夾角為偏移角，起動轉矩與偏移角成正比關系[12]，偏移角越大則越有利于提高電機起動性能。因此，與均勻氣隙結構相比，漸變氣隙使齒槽轉矩波形畸變，導致峰值增大和過零點偏移。

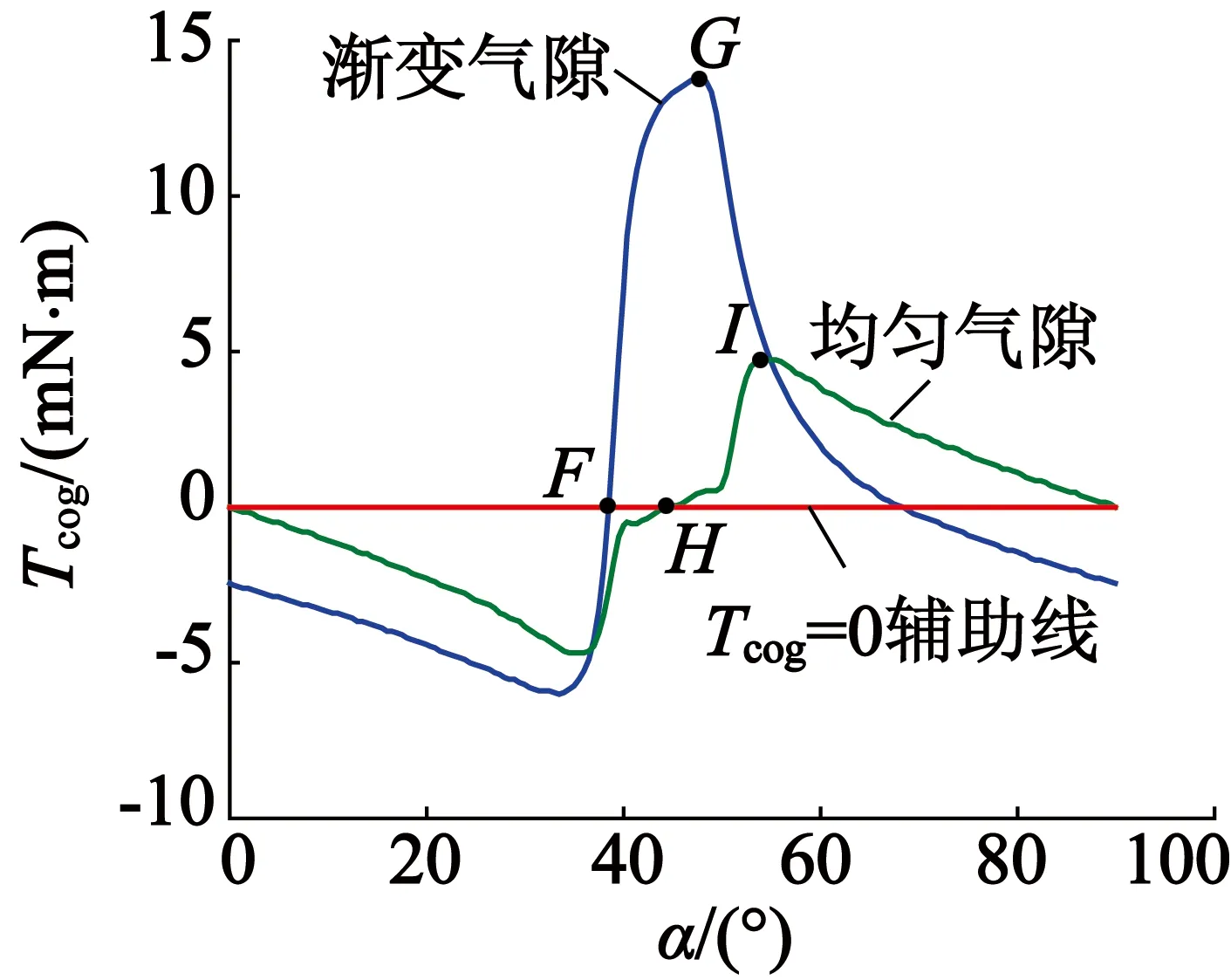
圖5兩種氣隙結構下的齒槽轉矩有限元解

2.2 解析解與有限元解對比分析

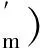
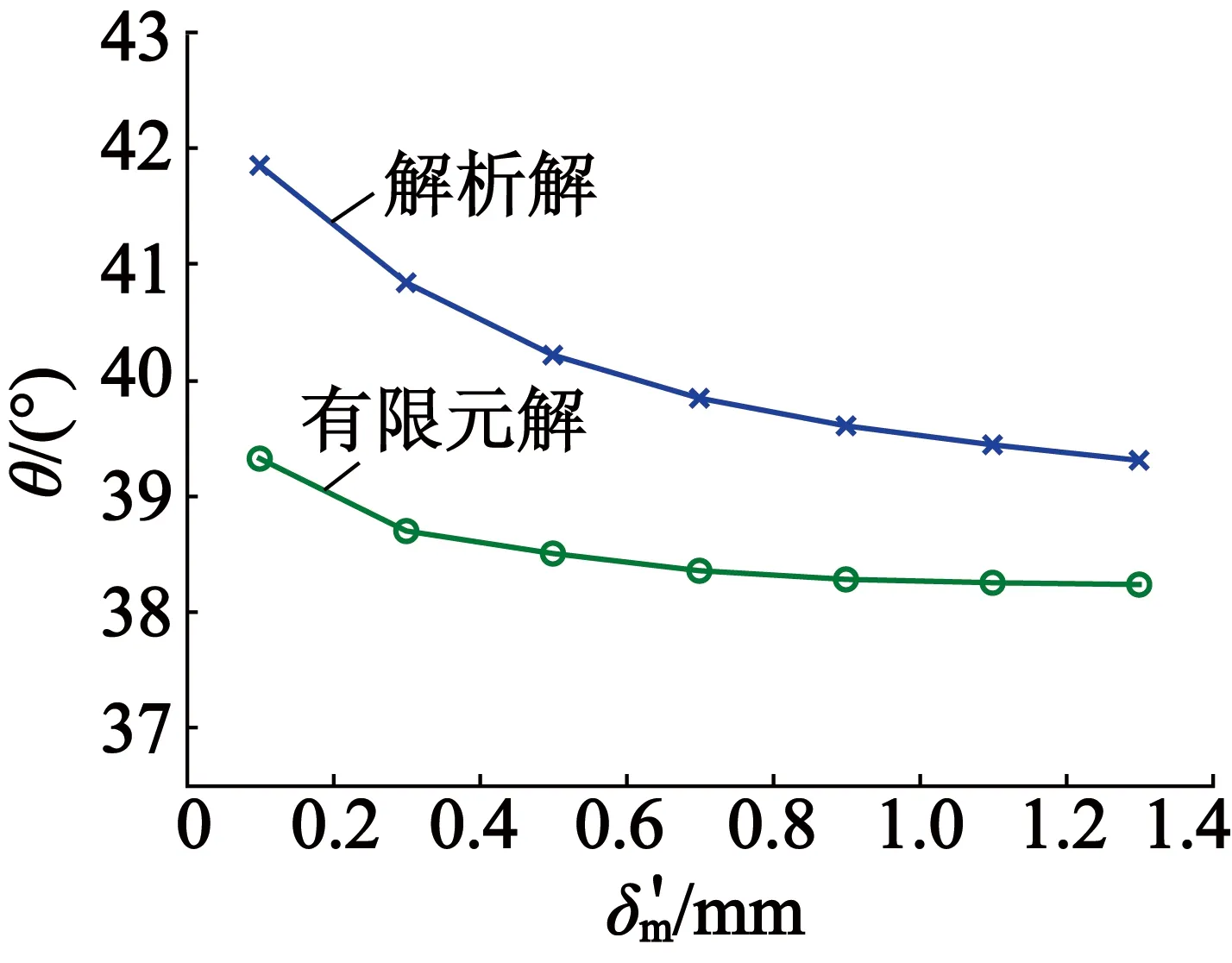
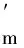
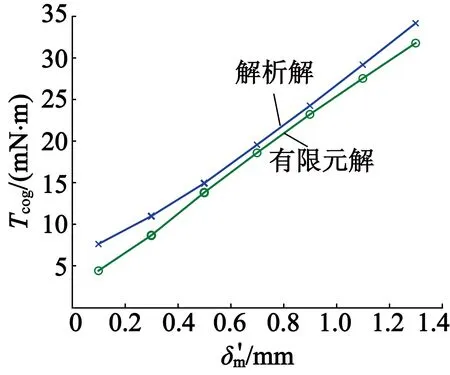
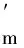
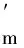
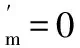
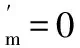
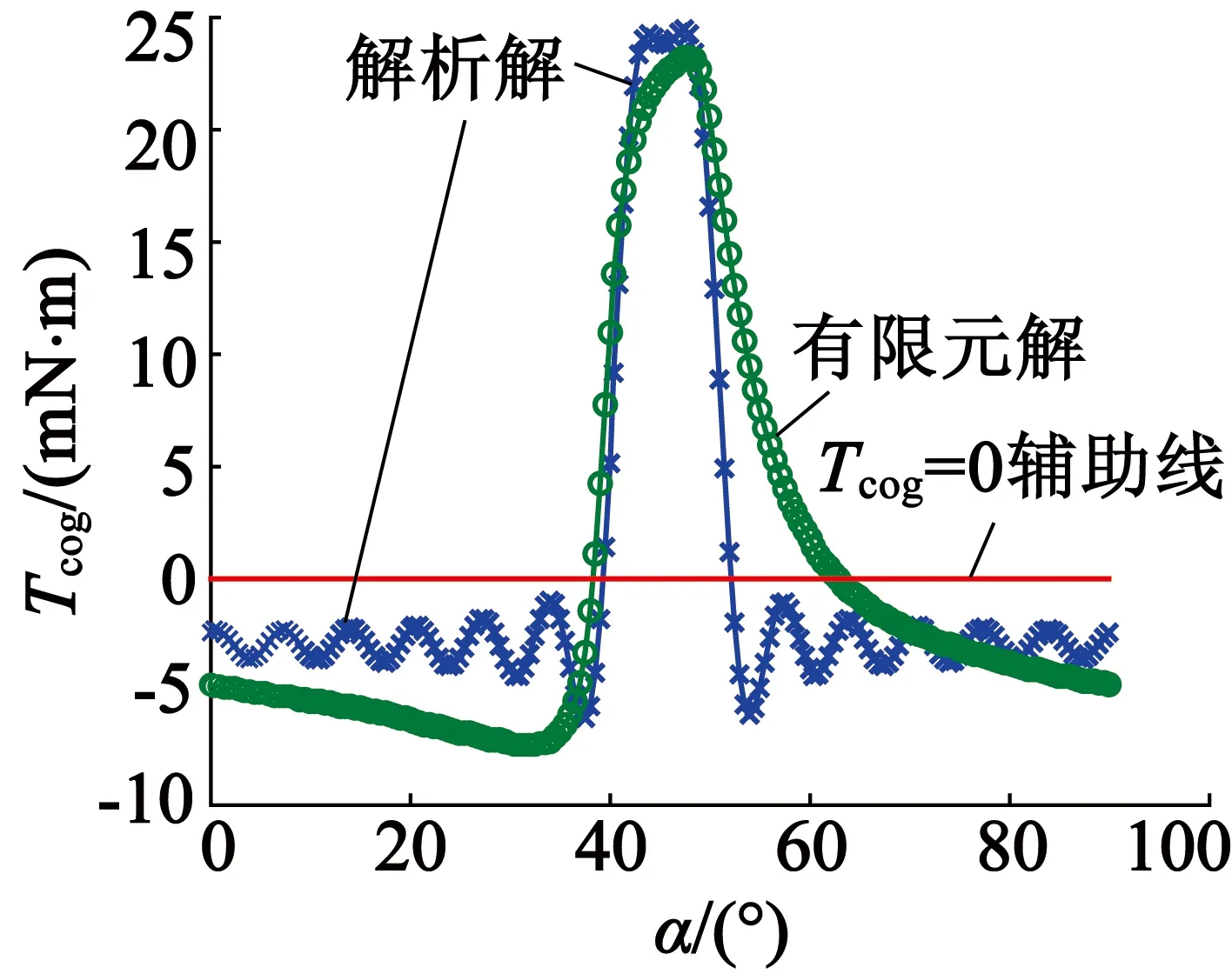
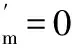
3 結 語

本文對漸變氣隙的SPBLDCM的齒槽轉矩研究表明：

1) 由于Ns=p，極槽數配合、不等齒寬、極弧系數優化等在三相無刷直流電動機中常用的齒槽轉矩削弱方法，在漸變氣隙的SPBLDCM中無效或效果不明顯；

[1] FAZIL M,RAJAGOPAL K R.Development of external rotor single-phase PM BLDC motor based drive for ceiling fan[C]//Joint International Conference on Power Electronics,Drives and Energy Systems.IEEE,2010:1-4.

[2] BENTOUATI S,ZHU Z Q,HOWE D.Influence of design parameters on the starting torque of a single-phase PM brushless DC motor[J].IEEE Transactions on Magnetics,2000,36(5):3533-3536.

[3] KWON B I,YANG B Y,PARK S C,et al.Novel topology of unequal air gap in a single-phase brushless DC motor[J].IEEE Transactions on Magnetics,2001,37(5):3723-3726.

[4] FAZIL M,RAJAGOPAL K R.A Novel air-gap profile of single-phase permanent-magnet brushless dc motor for starting torque improvement and cogging torque reduction[J].IEEE Transactions on Magnetics,2010,46(11):3928-3932.

[5] 賴文海,黃開勝,胡函武,等.基于輔助槽偏移的單相永磁同步電動機齒槽轉矩削弱[J].微特電機,2015,43(9):11-14.

[6] AHMED S,LEFLEY P.Study of the impact of asymmetrical stator pole arc on the cogging torque for single phase Permanent Magnet 無刷直流電動機 Motor[C]//International Conference on Electric Power and Energy Conversion Systems.IEEE,2009:1-4.

[7] 朱莉,姜淑忠,諸自強,等.表面式永磁電機齒槽轉矩解析模型比較[J].微電機,2010,43(1):10-15.

[8] ZHU L,JIANG S Z,ZHU Z Q,et al.Analytical methods for minimizing cogging torque in permanent-magnet machines[J].IEEE Transactions on Magnetics,2009,45(4):2023-2031.

[9] 楊玉波,王秀和,丁婷婷,等.極弧系數組合優化的永磁電機齒槽轉矩削弱方法[J].中國電機工程學報,2007,27(6):7-11.

[10] 楊玉波,王秀和,朱常青.基于分塊永磁磁極的永磁電機齒槽轉矩削弱方法[J].電工技術學報,2012,27(3):73-78.

[11] WANG D,WANG X,QIAO D, et al.Reducing cogging torque in surface-mounted permanent-magnet motors by nonuniformly distributed teeth method[J].IEEE Transactions on Magnetics,2011,47(9):2231-2239.

[12] 譚建成.永磁無刷直流電動機技術[M].北京:機械工業出版社,2011.