分數階滑模趨近率在SMVS-DTC中的應用

諸德宏，歐陽中萃

(江蘇大學，鎮江 212013)

0 引 言

永磁同步電機(以下簡稱PMSM)具有體積小、效率高、可靠性高、易于散熱、易于維護等優點,在交流伺服系統中獲得廣泛應用。直接轉矩控制(以下簡稱DTC)計算量小，響應速度快，對電機參數變化具有一定的魯棒性，是受歡迎的電機控制方法之一。然而傳統的DTC存在系統抖動太大，開關頻率不恒定，起動時有較大的沖擊電流等缺點。

為解決這些問題，近些年來人們提出了多種方案，如改進空間電壓矢量開關表、引入多電平逆變器、滑模變結構控制、自適應控制、模糊控制等。其中，基于滑模變結構的DTC以算法簡單、響應速度快、對參數及擾動不靈敏等優點受到諸多關注。文獻[1]用兩個滑模控制器替代傳統DTC中的滯環調節器，來解決以上問題。文獻[2]在滑模控制器引入積分項，利用積分滑模面平滑的特性來削弱抖振，同時通過調節初始值的大小，使系統初始狀態位于滑模面上，縮減了趨近運動的時間。文獻[3-5]用分數階積分項來替換滑模控制器中的傳統的整數階積分項，利用分數階系統中舊誤差累積會隨時間緩慢衰減的特性來抑制傳統積分滑模控制器中積分飽和的現象，從而達到提高滑模控制性能目的，但由于滑模變結構技術的應用，會不可避免地存在抖振問題。文獻[6]指出了趨近率的不足，分析了傳統趨近率產生抖振的本質原因，并設計了兩種新型滑模趨近率。文獻[7]則以航天器姿態控制系統為控制對象，將分數階微分方程和傳統等速趨近率相結合提出了分數階趨近率概念，仿真結果顯示分數階趨近率不僅可以柔化系統運動軌跡，減小暫態過程中的超調量，同時還可以改善系統抖振現象。文獻[8-9]針對Lorenz電路等不同形式的混沌系統對分數階趨近率進行一系列的研究。上述文獻雖然不同程度地涉及到分數階趨近率，但還未有專門的文獻針對基于分數階趨近率的滑模控制器在PMSM中的應用特性進行研究。

本文在文獻[3-5]分數階滑模控制器基礎上，結合文獻[7-9]分數階趨近率設計一種改進型的分數階滑模控制器。首先分析了分數階指數函數曲線特性圖，從理論上證明了它的收斂性和平穩性，然后通過和傳統的指數趨近率對比仿真來驗證這些特性，最后以PMSM為控制對象使用Simulink仿真軟件來驗證該控制方法的可行性。

1 數學模型

1.1 PMSM數學模型

本文的PMSM采用三相交流電，定子采用星形接法。為方便數學建模，忽略磁路飽和、渦流、磁滯損耗、阻尼繞組以及高次諧波的影響，則PMSM在α-β坐標系下的狀態方程：

式中：uα，uβ，iα，iβ分別為α-β坐標系下的定子電壓、電流；Ld，Ld分別為d-q坐標系下的等效電感；Rs，ψf分別為定子電阻和永磁體磁鏈系數；eα，eβ為拓展反電動勢[1-3],其值：

α-β坐標系下PMSM轉矩方程：

ψαiβ-ψβiα) (3)

θ為轉子磁鏈與x軸之間的夾角；p為電機磁極對數。

1.2 分數階微積分定義

分數階微積分是對古典微積分的拓展和延伸，使得古典微積分的階次從正整數推廣到了任意實數乃至復數。大多數情況下，在對實際系統建模過程中，古典微積分只能建立近似的數學模型，而分數階微積分才能建立更加精準的數學模型[6]。

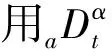
dtαR(α)>0

1 R(α)=0

式中：a，t分別為微積分的下限和上限;α是微積分的階次；R(α)為任意復數α的實部。

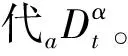
由于分數階微積分的特殊性，至今還未有統一的定義，人們根據不同的應用需求和限制條件,推導出了形式不同的分數階微積分定義，現在主要有Grunwald-Letnikov型、Riemann-Liouville型和Caputo型這3種[10]定義。

1) Grunwald-Letnikov型定義

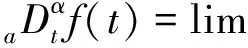
jf(t-jh) (5)

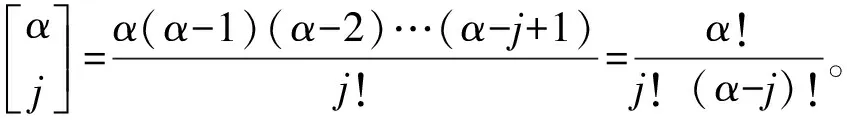
2) Riemann-Liouville型定義

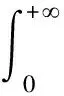
3) Caputo型定義

本文采用GL型的定義對分數階滑模趨近率進行數值上的計算，采用C型的定義對分數階系統微分方程進行數值計算。

GL型定義下的Laplace變換：

L{Dαf(t)}=sαF(s) (8)

式中：F(s)為f(t)的Laplace變換;sα為分數階微積分算子。

1.3 分數階指數函數的特性

分數階微積分最基礎的單元形式就是基本分數階微分方程，對基本分數階微積分方程求解不僅能夠讓我們很好的了解其特性，并且在求解其他的分數階微積分方程具有很重要的意義，還能為改進分數階滑模控制器提供重要的依據[8]。

所有初始條件為0，并且忽略記憶因素影響的情況下，基本分數階微分方程：

Dαx(t)=-αx(t)+bu(t) (9)

傳遞函數：

可以利用下式進行反拉氏變換：

對式(10)反拉普拉斯變換：

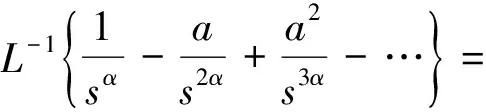
并定義：

對式(9)兩邊同時求Laplace變換：

sαX(s)-x0=-aX(s)+bu(s) (14)

化簡：

(sα+a)X(s)=x0+bu(s) (15)

兩邊同時乘以F(s)進一步化簡：

X(s)=F(s)x0+F(s)bu(s) (16)

對式(14)求Laplace逆變換，解得：

式中:x0=[Dα-1x(t)]t=0，可以解出其解析解:

由式(18)通過MATLAB可以得到其解的曲線,如圖1所示。

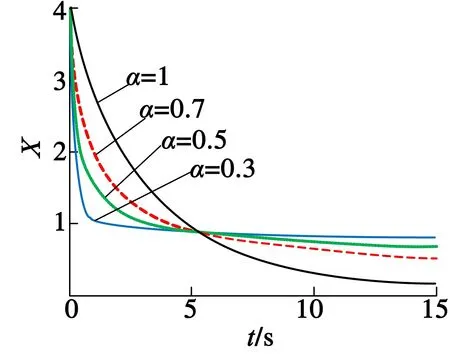
(a)a=-4

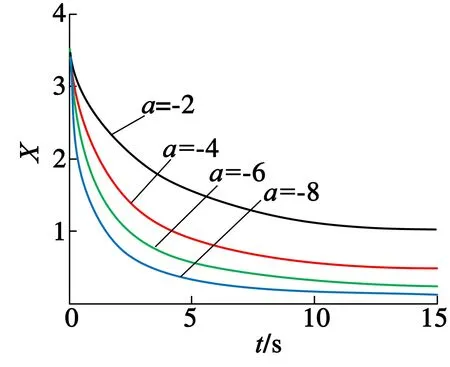
(b)α=0.5

圖1不同階次不同系數的解

由圖1可以看出，分數階指數函數曲線形狀與整數階的指數函數曲線形狀十分類似，并且當參數a固定時，微分階次α越小，下降速度越快，趨于穩定時的速度越緩慢，而這正好與趨近率的設計要求一致。

2 分數階滑模控制器的設計

2.1 趨近率的設計

趨近率作為滑模控制的最基本組成部分之一，反映了系統以何種方式到達滑模面。在趨近過程中，通常希望系統遠離滑模面的時候，趨近速度盡可能得快；而在接近滑模面的時候，又希望趨近速度能盡可能地減小為零，以免造成較大的沖擊，從而達到抑制抖振的目的。

從分數階指數函數曲線特性以及分數階微積分的定義可以看出，分數階微分方程十分符合這一要求，因此，不難想到將分數階微分方程和傳統指數趨近相結合，與指數趨近率相比，這種趨近率收斂速度應該更快，且更加平滑，后面的仿真結果也證明了這點。現給出分數階趨近率如下：

Dαs=-ks-εsgn (s)(k>0，ε>0，0<α<1) (19)

2.2 滑模面的設計

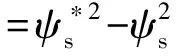
s=sT

ss=eT+c1D-α

eψ+c2D-α(20)

式中:c1，c2為分數階積分系數；α為分數階積分系數，0<α<1。

選擇式(19)的分數階趨近律：

對sT和sψ分別求導，得：

將式(1)代入式(22)可得：

U1=-B-1A1+F1+D1-α(KTS+εTsgn(s))

A2+F2+D1-α(KψS+εψsgn(s)) (23)

其中：

為了能更清楚的說明分數階趨近率的有優點，先給出文獻[3]中改進前的控制率方程，方便后面的對比仿真。選取傳統的指數趨近率：

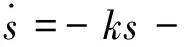
ε·sgn(s)

(27)

同理可得：

其控制率為:

2.3 穩定性分析

sT[D1-α(-kTs-εTsgns)]+

sψ[D1-α(-kψs-εψsgns)] (30)

由式(7)可以推導出：

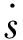
利用sgn [D1-α(-ks-εsgns)]=-ks-εsgns[7]可以對等式進一步化簡：

sgnsT[D1-α(-kTs-εTsgns)]+

sgnsT[D1-α(-kTs-εTsgns)]=

sgns(-kTs-εTsgns)+

sgns(-kψs-εψsgns)=-kTs-

εTsgns·sgns-

kψs-εψsgns·sgns(32)

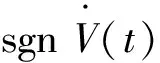
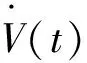
3 仿真分析

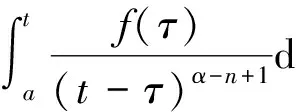
為了驗證改進后的分數階滑模控制器的控制性能，將它和改進前的分數階滑模控制器在Simulink中進行對比仿真。系統控制原理結構框圖如圖2所示，所用PMSM參數：定子電阻Rs=0.98 Ω；母線電壓udc=300 V；極對數p=4；交、直軸電感Ld=Lq=0.008 5 H；轉動慣量J=0.008 kg·m2;磁鏈給定值ψf=0.175 Wb；負載給定轉矩T*=10 N·m；轉速給定值nN=500 r/min 。

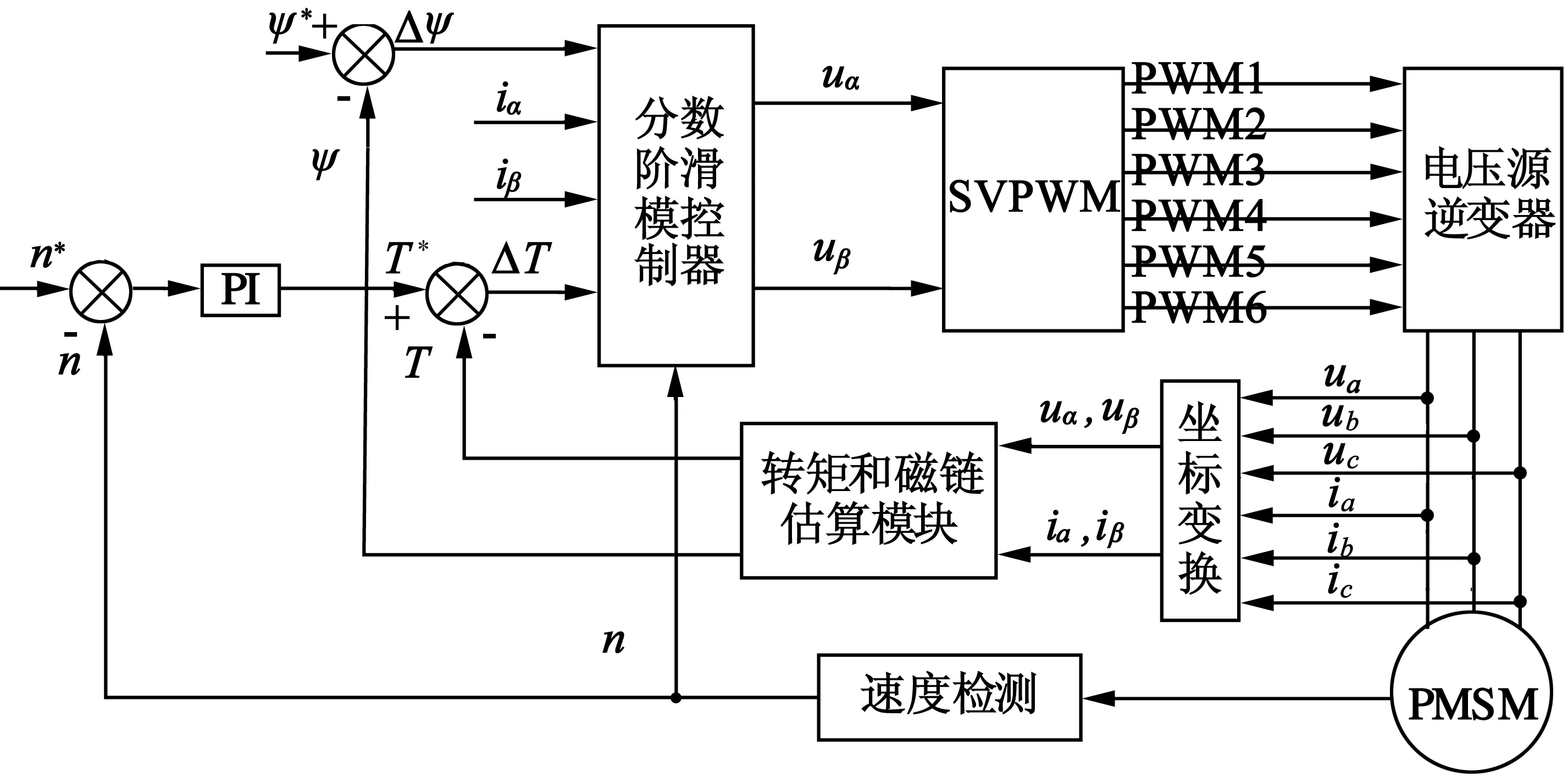
圖2基于分數階趨近率的分數階滑模變結構系統控制框圖

設置電機空載起動，仿真時間為0.2 s，給定磁鏈ψ*=0.175，給定轉速為n*=500 r/min，分數階階次λ=0.95。滑模面采用分數階滑模面，趨近率分別采用指數趨近率和分數階趨近率來進行對比仿真，圖3～圖6分別為系統定子磁鏈軌跡、定子電流波形、轉速波形和電磁轉矩波形。

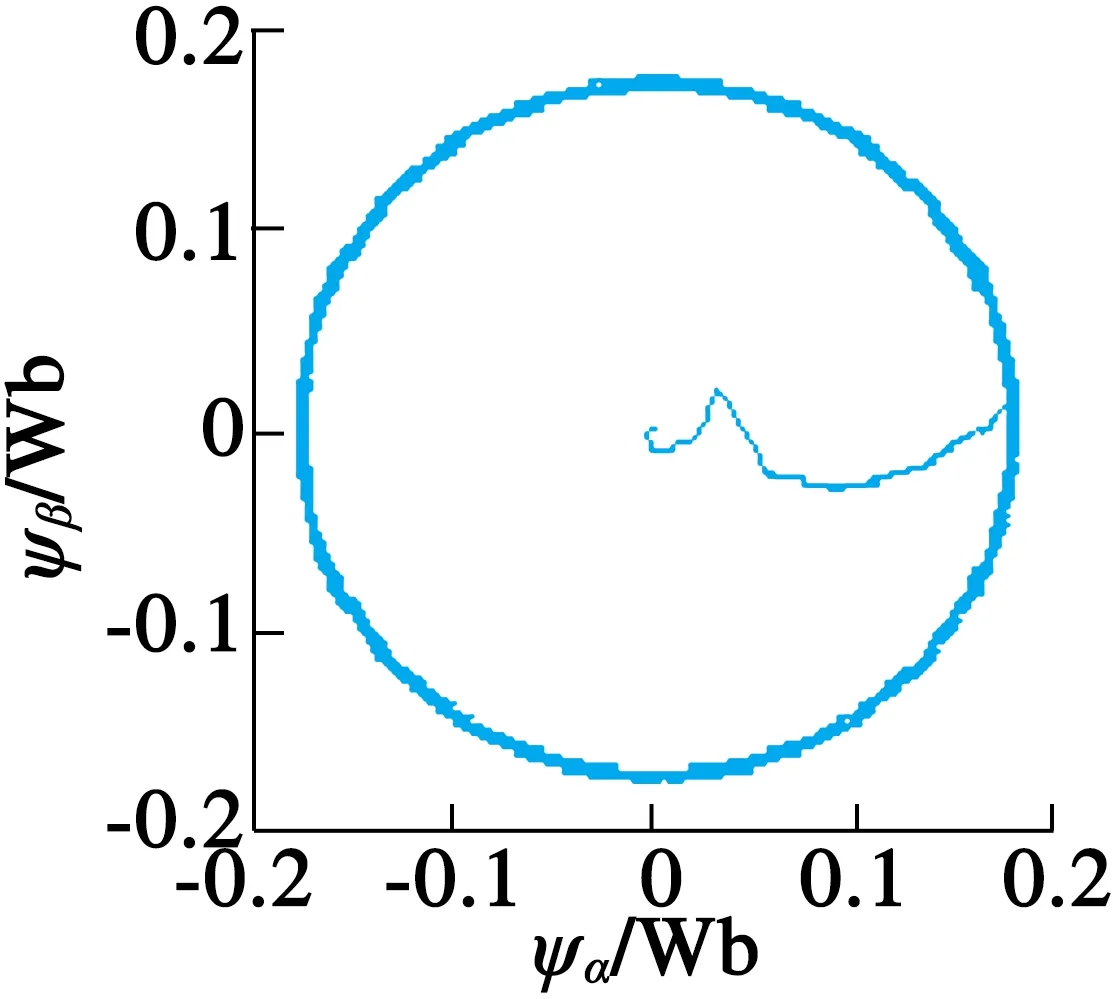
(a) 改進前

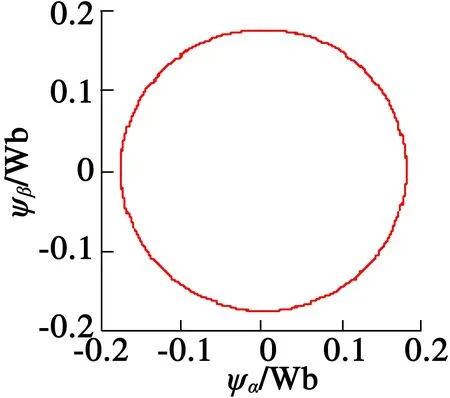
(b) 改進后

圖3定子磁鏈軌跡圖

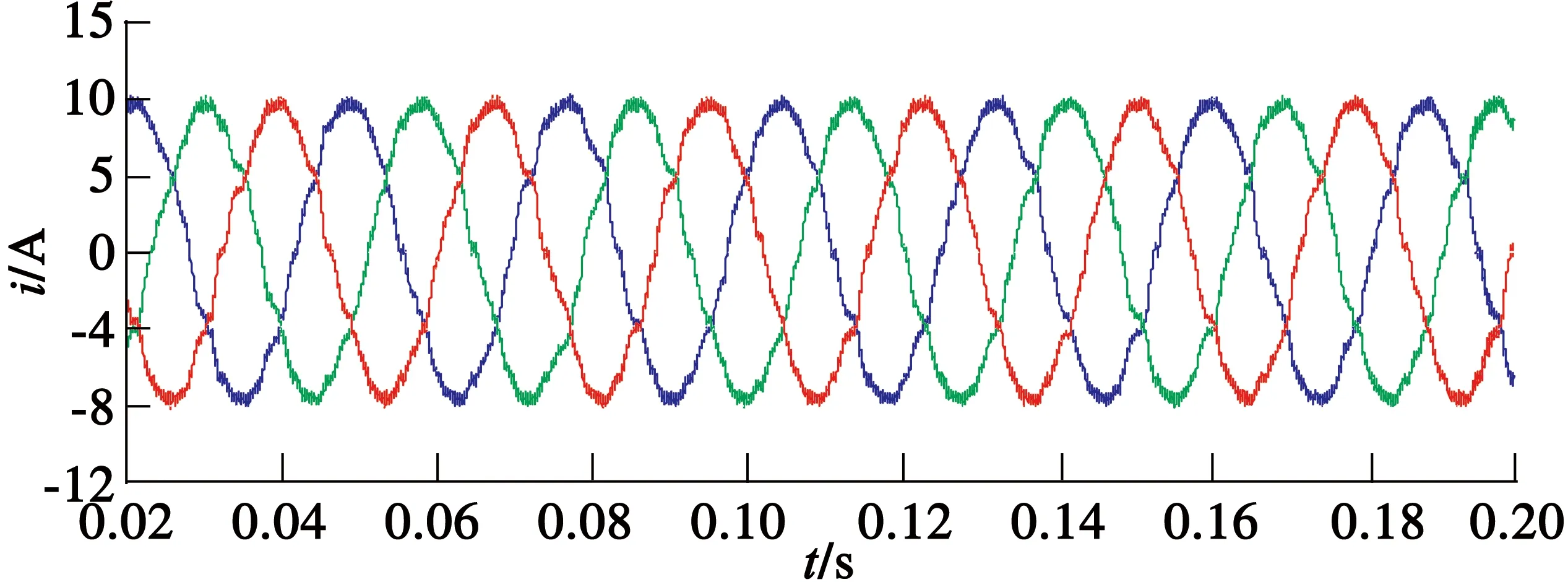
(a) 改進前

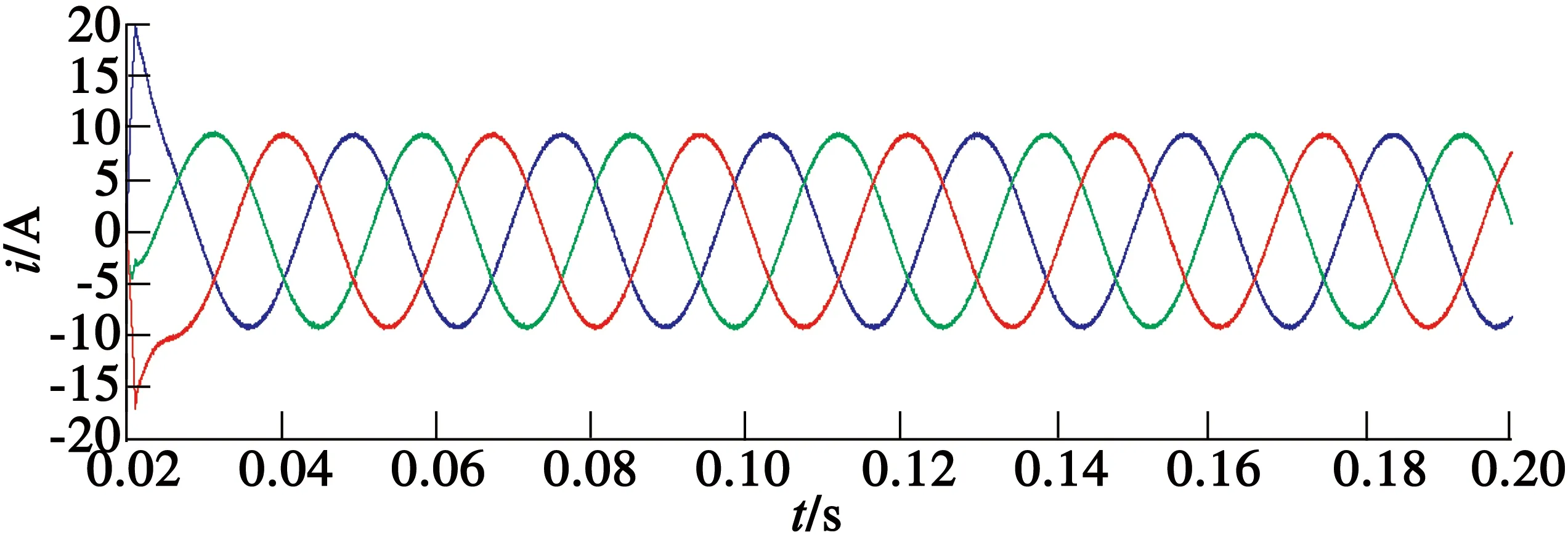
(b) 改進后

圖4定子電流波形

圖5轉速曲線

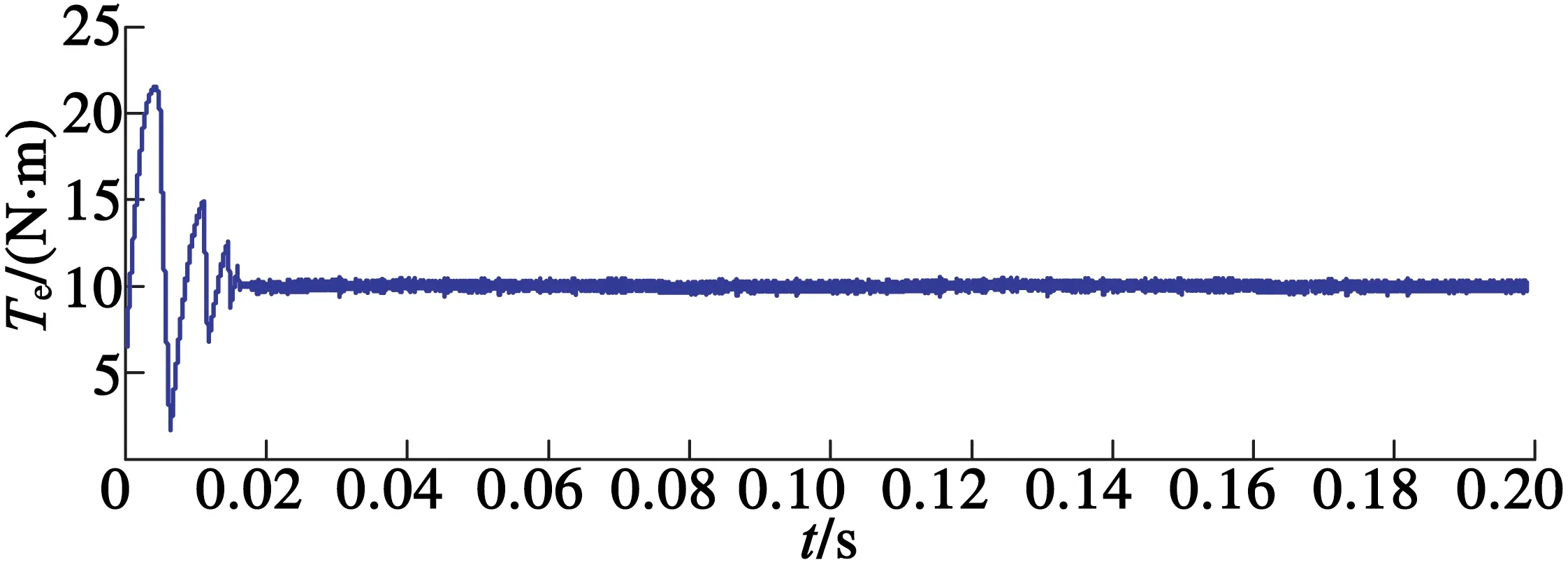
(a) 改進前

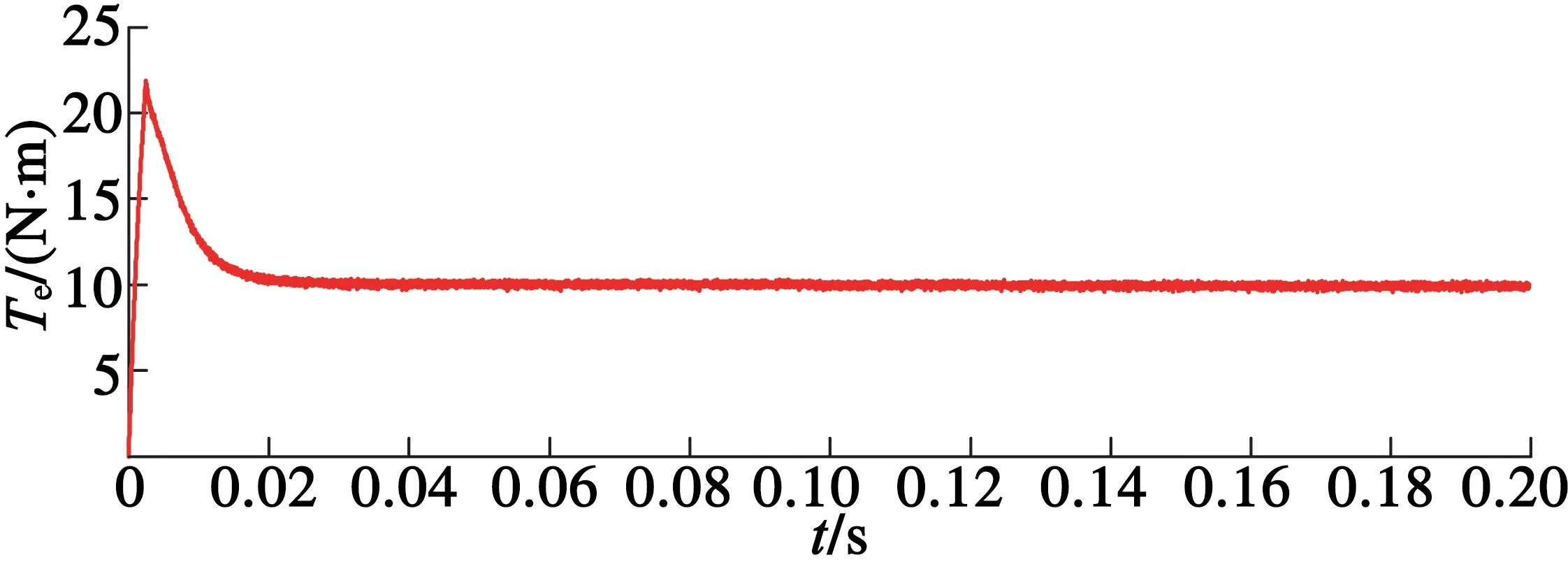
(b) 改進后

圖6電磁轉矩圖

從圖3～圖6可以看出,分數階滑模面和分數階趨近率相結合的方法能使系統收斂較快，其轉速和轉矩波動也比較小。從圖4(a)和圖4(b)的對比也可以看出,改進后分數階滑模控制器能使定子電流波形更加平滑。

為了驗證動態特性，系統穩定運行后，對給定的負載轉矩進行突變，然后觀測其運行效果。圖7和圖8分別是給定的負載轉矩在0.1 s時從10 N·m突然增加到15 N·m的轉矩響應曲線以及電機轉速響應曲線。

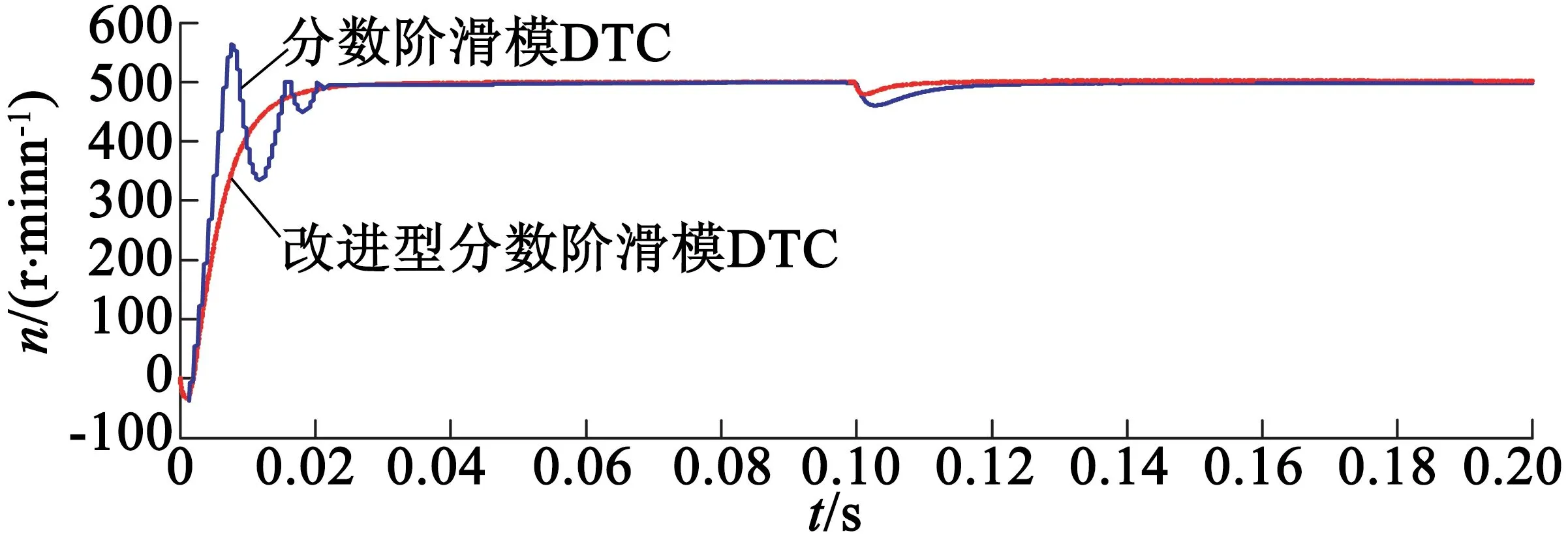
圖7突加負載時轉速響應圖

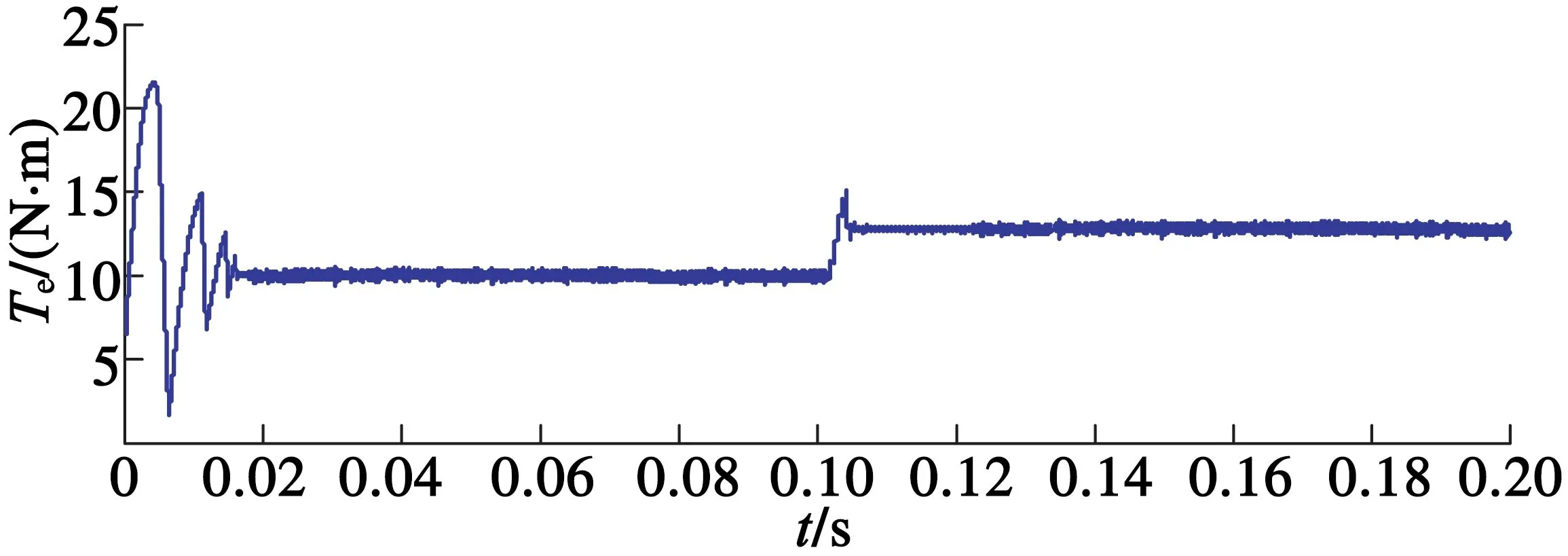
(a) 分數階滑模DTC

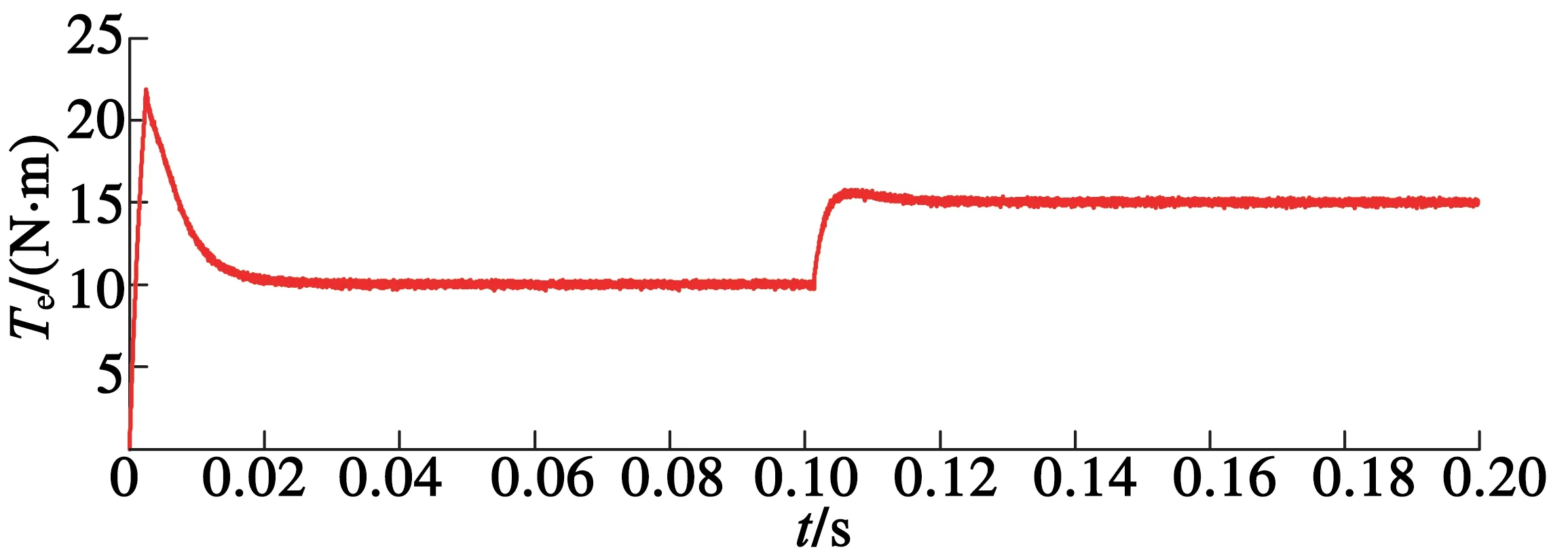
(b) 改進型分數階滑模DTC

圖8突加負載時轉矩響應圖

從圖7、圖8可以看出,分數階滑模面和分數階趨近率相結合能明顯減小轉速和轉矩脈動，系統響應速度也比改進前的要快。通過對比不難看出,改進后的分數階滑模控制器對參數突變帶來的外部干擾有更好的魯棒性，具有更好的抗干擾能力。

從以上的仿真結果可以看出，用分數階趨近率替代傳統指數趨近率，構建的新型分數階滑模控制器，不僅保留了轉矩、磁鏈抖振小等原有的性能，而且還能提高系統收斂速度、減小超調量、柔化了運動軌跡，提高了PMSM調速性能。

4 結 語

改進后的滑模控制器充分利用了分數階微積分具有微分和積分兩個可變的自由度的性質。

在滑模切換面的設計中引入分數階積分項，利用分數階積分方程中積分階次越小，下降速度越快，趨于穩定時的速度越緩慢的性質，不僅保留了原來積分滑模控制器中原有的優點，還很好地抑制傳統積分滑模控制器中存在的積分飽和的問題。

在趨近率設計中引入分數階微分方程，利用分數階微分特性，使得系統在遠離滑模面時能更快地到達滑模面，接近滑模面時趨近速度又比較小，從而抑制因為沖擊帶來的抖振。

[1] 賈洪平,賀益康.永磁同步電機滑模變結構直接轉矩控制[J].電工技術學報,2006,21(1):1-6.

[2] 李政,胡廣大,崔家瑞,等.永磁同步電機調速系統的積分型滑模變結構控制[J].中國電機工程學報,2014(3):431-437.

[3] HUANG J,XU Q,SHI X,et al.Direct torque control of PMSM based on fractional order sliding mode variable structure and space vector pulse width modulation[C]// Control Conference.IEEE,2014:8097-8101.

[4] 鄧立為.分數階滑模控制理論及其應用研究[D].哈爾濱:哈爾濱工業大學,2014.

[5] 張碧陶,皮佑國.基于分數階滑模控制技術的永磁同步電機控制[J].控制理論與應用,2012,29(9):1193-1197.

[6] 孫力.永磁同步電機調速系統滑模變結構控制若干關鍵問題研究[D].哈爾濱: 哈爾濱工業大學,2014.

[7] 宋申民,鄧立為,陳興林.分數階微積分在滑模控制中的應用特性[J].中國慣性技術學報,2014(4):439-444.

[8] 顧文軍.Lorenz混沌電路的分數階控制[D].南京:南京林業大學,2012.

[9] AGHABABA M P.Finite-time chaos control and synchronization of fractional-order nonautonomous chaotic (hyperchaotic) systems using fractional nonsingular terminal sliding mode technique[J].Nonlinear Dynamics,2012,69(1-2):247-261.

[10] 張文芳.分數階微積分概念的起源和演化[D].西安：西北大學,2014.

[11] TEPLJAKOV A,PETLENKOV E,BELIKOV J.FOMCON:Fractional-order modeling and control toolbox for MATLAB[C]//Proceeding of 18th Int Mixed Design of Integrated Circuits and Systems (MIXDES) Conference.2011:684-689.