連桿機構預定軌跡設計及仿真

聶晶晶 武漢商學院機電工程與汽車服務學院

在中國，連桿機構的應用可以追溯到兩千年前，歐洲在中世紀也有對連桿機構的研究，例如張衡發明的地震儀，橢圓車削裝置，都采用了平面連桿機構。在現代，連桿機構的應用日益廣泛，如在仿生學上，連桿機構可以實現人類關節功能，在設計機器人四肢時，往往優先選擇連桿機構。

在20世紀80年代，對連桿機構的研究主要集中在設計、運動規律、分析、廓線的綜合等四個研究方向；到90年代，出現了大量的動力學、振動、優化設計、誤差分析和CAD/CAM等研究論文；近些年，對平面四桿機構的共軛曲面原理、專家系統、動態仿真、可靠性分析也有了更多的研究。

1 連桿機構設計

四桿機構設計常用的方法有解析法、圖解法和圖譜法。解析法的精度比較高，但是由于連桿曲線是高階曲線，建立方程的過程比較繁瑣，計算量很大；圖解法很直觀，比較容易理解，但由于作圖誤差的存在不可避免，作圖法的精度比較低；圖譜法比較簡單，但是圖譜本身有限，不可能將所有的連桿曲線包含在內，因此也不能滿足所有設計要求。

生產制造中要實現的連桿曲線軌跡是多種多樣的，每次所給的限制條件和初始條件也不相同，按照常見設計類型將平面連桿機構的運動設計分為以下三類問題：

（1）要求所設計構件能夠帶動某一個構件經過給定的若干個位置坐標。

（2）按照事先確定的函數關系來設計從動件和主動件的運動關系（包括位置，速度和加速度）。

（3）要求所設計的連桿能夠帶動某桿上的某一點按照一個給定的運動軌跡（比如圓，橢圓，直線等）來運動。

平面連桿設計包括運動方法設計和運動尺寸設計。運動方法設計實在設計機械過程中，當工藝動作確定之后，選擇適宜的連桿機構的結構形式，包括構件數目以及運動副的類型和數目。運動尺寸設計是在運動方案設計基礎上，根據機構要完成的運動而提出的設計條件，確定機構運動簡圖及其參數。

矢量用于表示一個具有大小和方向的物理量。一個位移矢量表示了空間任意兩點之間的有向距離。連桿機構中的每一根桿都可以看作是一個位移矢量，一斷作為起點，另一端作為終點。這個桿長就是位移矢量的大小，而連桿的夾角規定為矢量與x軸正向間的夾角就是（逆時針為正）。

2 連桿機構計算

在工業中，為了實現某種特殊工藝要用連桿機構來實現一條確定的運動軌跡是常見的機械設計問題，常見于間歇機構和連續機構的設計中，能否準確的實現運動軌跡是工業控制能否精確控制的前提條件。因此，研究如何設計和實現連桿軌跡是非常實用的。、

現在設計一個如圖所示一個曲柄搖桿機構，當AB整周旋轉時，要求BC桿上的點E實現給定的運動規律，連桿機構如圖中所示。

圖1 連桿機構簡圖

在這里要確定的值有連桿機構中各桿桿長L1,L2,L3,L4，以及各桿初始角度θ1,θ2,θ3,以及連桿上的點E與BC桿的夾角ψ。在建立數學模型函數時，保證桿BC上E點的實際軌跡與給定軌跡之間坐標值誤差均方根值最小，并設置曲柄搖桿機構存在的約束條件。用MATLAB軟件編寫M文件計算出四桿的桿長以及夾角。

計算得出的數據如下：

L0=51.7,L1=8,L2=53.6,L3=25.62,L4=22.7,θ1=38.65°。

根據曲柄連桿機構的結構得出初始角度如下：

(b)The endoscopic appearance of atrophic gastritis showed red and white mucosa,mainly white mucosa,the folds became flat or disappeared,and some mucosal blood vessels were exposed,which could be accompanied by particles or nodules.

計算得到θ3′=?82.24°; θ3′′′=69.65°;根據連桿運動機構的連續性，選擇θ3=69.65°。

同理計算θ2

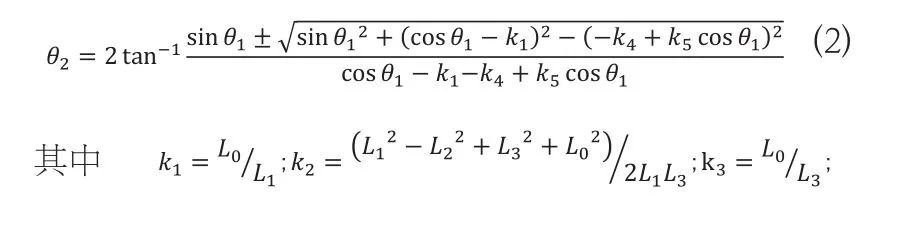
計算得到θ2'=-53.59°;θ2'''=43.87°;根據運動機構的連續性，選擇θ2=69.65°。

使用Simulink仿真。

為了方便使用Simulink進行仿真，首先對連桿機構建立閉環矢量方程

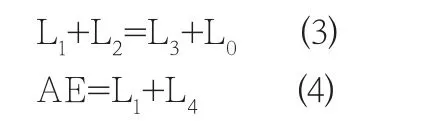
對矢量方程求導，得到連桿機構運動的角速度方程。經過整理得到矩陣方程如下：

式（5）為連桿機構的數學模型。表示連桿機構四桿的位置關系，以及運動過程中各桿時間角速度的關系。

式（6）為連桿機構上BC桿上的一點E點的數學模型，表示了E點的x,y軸坐標值，φ角是E點與BC桿之間的夾角。

三、連桿曲線仿真

在MATLAB軟件中編寫M文件1.m和2.m分別描述連桿機構以及點E的數學模型。接著進入MATLAB軟件中的SIMULINK仿真模塊，調用之前編寫的M文件并根據連桿機構的運動關系建立仿真模型。

設置仿真初始值，將θ1，θ2和θ3的角度改成弧度，θ1=0rad，θ2=0.766rad，θ3=1.2156rad。設置過程如下圖所示：

圖2 設置θ2 初始弧度

圖3 設置θ3 初始弧度

在建立好仿真模型并設置好仿真的初始條件后，點擊SIMULINK下拉菜單中的start按鈕，軟件開始仿真，設置好合適的XY繪圖坐標區間以及取樣時間，可以得到光滑連續的仿真曲線，該模型仿真曲線如下圖所示：

圖4 仿真得到的連桿曲線

可以看到與我們所要得到的軌跡曲線形似，但是仍然有很多誤差。

3 總結

本文設計一個要求通過規定位置的連桿機構，通過MATLAB建模計算得到連桿機構的桿長以及初始角度后，使用SIMULINK模塊對連桿機構上一點M點所經過的軌跡進行仿真，得到連桿曲線，得到的曲線與給定位置形似，但仍然有誤差，后面將對誤差產生的原因以及縮小誤差的方法進行研究。通過研究發現，通過軟件建模計算連桿機構，之后再進行仿真的辦法要比傳統的解析法實現起來更加簡單，比圖譜法更加靈活，可以根據設計需求不斷修改數學模型，從而實現不同的連桿曲線運動軌跡。

[1]年大華,華志宏.連桿機構設計與應用創新[M].北京:機械工業出版社,2008.

[2]何珣，姚俊，張聲.基于SIMULINK平面五桿機構運動學仿真[J].湖北工業大學學報，2014，29（4）：18-22

[3]宋志強，基于 matlab 的平面四連桿機構優化設計[J]. 呼倫貝爾學院學報，2014，6：108-109