高速永磁同步電動機流場及溫度場分析

蘭志勇，王 琳，焦 石，魏雪環，陳麟紅

(湘潭大學，湘潭 411105)

0 引 言

高速永磁電機因其功率密度高，體積小，效率高，可靠性高，運行成本低，可直接與從動機相連的特點，在壓縮機、高速離心機等領域得到廣泛關注，高速電機已經成為電機領域的研究熱點。由于高速電機旋轉線速度比普通電機快，高速電機轉子旋轉引起的氣隙溫度是普通電機的幾倍甚至十幾倍，高速電機定轉子與空氣摩擦產生溫升在電機總溫升中占有很大比重[1]。同時，由于高速電機轉子體積小，散熱困難，特別是在全封閉電機中，永磁體過熱容易產生不可逆退磁[1-3]，因此必須要考慮空氣摩擦損耗產生的熱量，為電機設計及散熱提供依據。

目前國內對電機流場及溫度場的耦合研究缺乏具體使用的方法。楊平西等人利用非線性二次元回路壓降方法得到空氣流量，再經過氣體與固體之間對流分析，得到電機各節點溫度[4]，此方法在模型建立方面比較復雜，實用性不強；江有名等人采用有限體積法對流場及溫度場進行分析，找出二者關系，具有重要意義[5]。蘇虎等人采用Fluent對電機進行數值分析，改善散熱效果[6]。國外，M SHANEL等人利用Fluent對電機耦合場分析，得到控制電機內氣隙的流動可以改善風摩損耗[7]。BUMP J R等人采用納維斯托克斯方程對電機氣隙與定轉子之間熱對流關系進行分析，得到電機溫度場參數[8]。

本文利用計算流體動力學的方法(CFD)，通過多物理場耦合，對高速電機在各種轉速情況下的流場以及溫度場進行分析，得到電機氣隙轉速變化及風摩產生溫度對定轉子、繞組溫度的影響，為電機優化設計提供理論依據。

1 高速永磁電機轉子空氣摩擦損耗分析

相對高速電機，普通電機轉速低，空氣摩擦損耗較小，傳統電機的空氣摩擦損耗一般可由經驗公式或者電機實測得到，誤差在接受范圍之內。而高速電機，轉速可達每分鐘幾十萬轉，空氣摩擦損耗占據總損耗的比例較大，并且高速旋轉的轉子會引起電機氣隙內空氣的切向流動導致空氣與轉子產生切向摩擦力，這都是高速電機空摩擦損耗的組成部分。而普通電機的經驗公式沒有考慮到空氣與轉子的切向摩擦力以及在有槽電機情況下，轉子轉動引起的槽內空氣渦流產生的損耗。

高速電機氣隙中空氣流動狀態分為層流和湍流兩種狀態，可通過雷諾數(Reynolds number)來判斷：

(1)

式中：ρ為流體密度；υ為空氣流速；L為特征長度；μ為空氣動力粘度。

對于電機氣隙內空氣流動，通常認為雷諾數Re高于2 300為湍流，低于2 300為層流[9]。本文采用的電機模型為全封閉式模型，不存在軸向通風，徑向雷諾數為3 701，屬于湍流范圍。

轉子在高速運行狀況下帶動氣隙內空氣流動形成湍流，空氣屬于黏性氣體，因此在轉子高速旋轉時，定轉子表面空氣形成黏性層，相對速度與定轉子表面一致，氣隙中間部分的空氣則為湍流層[10]。因此可以假定空氣與電機定轉子之間為無滑移邊界條件，轉子表面的空氣流動速度與轉子轉動線速度相同，定子表面空氣流動速度與定子相對速度保持一致。

2 電機氣隙流場模型的建立

高速電機氣隙流場模型的建立主要包括以下3個方程[11]。

質量守恒方程：

(2)

動量守恒方程：

(3)

式中：p為空氣靜壓；τij為應力張量。式(3)中的應力張量由下式給出：

(4)

能量守恒方程：

(5)

式中：cp為空氣比熱容；T為氣隙內溫度；k為氣隙內空氣的散熱系數。

由空氣動力學可知，空氣都可被看成牛頓流體,將牛頓第二定律代入電機氣隙模型內可導出電機氣隙流動的動量方程,也稱納維斯托克斯方程[12](N-S方程)：

(6)

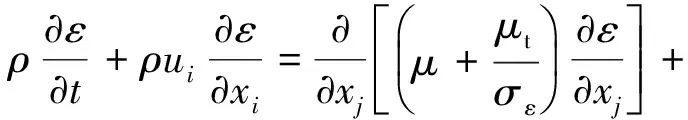
(7)

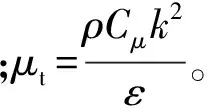
C1ε與流動情況有關:

(8)

(9)

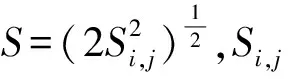
流體仿真及邊界條件設置：

(1) 電機定轉子之間氣隙由轉子高速旋轉帶動空氣流動，氣隙設為全流動，氣隙與定轉子接觸部分為運動邊界，假定表面粗糙度。

(2) 在氣隙的運動面上指定轉子的旋轉速度，其他面為靜止面。

(3) 空氣與電機定轉子之間為無滑移邊界條件，轉子表面的空氣流動速度與轉子轉動線速度相同，定子表面空氣流動速度與定子相對速度保持一致。

(4) 由于高速電機最高轉速為18 000 r/min，計算得電機轉子表面旋轉線速度為102.7 m/s，低于音速，在本模型中認為不可壓縮流體。

(5) 由于高速電機旋轉速度大，標準壁面函數在高速電機氣隙內不適用，故在本模型中適用非平衡壁面函數。

(6) 不考慮重力的影響。

根據以上理論依據及邊界條件假設，取電機氣隙模型如圖1所示。因本文采用模型為有槽電機模型，斜槽數為1 ，因此在計算轉子空氣摩擦損耗時，需將損耗分為兩部分，即電機非槽口處的空氣摩擦損耗及槽口處的空氣摩擦損耗。

圖1 電機氣隙模型

轉子表面的空氣流動速度與轉子轉動線速度相同，定子表面空氣流動速度與定子相對速度保持一致。將氣隙分為動靜兩區域，區域之間的交界面為流固耦合固體面和流固耦合流體面，以這兩個邊界面為交接面來計算交界面處的解[13]，由ANSYS Fluent有限元分析得到電機非槽口處氣隙的空氣流動速度。

3 電機溫度場模型建立

3.1 電機溫度場計算模型

由于電機內部對流傳熱非常復雜，需對電機對流傳熱過程進行以下簡化分析[14-16]：

(1)電機內部各材料傳導介質均為各同向性；

(2)電機內部只存在對流，不存在輻射；

(3)電機軸向溫度分布均勻；

(4)不考慮定子槽對溫度梯度的影響。

根據以上假設，得到電機溫度層熱傳導方程：

(10)

式中：λ為各介質之間熱傳導率；T0為表面上給定的溫度；α為表面上的散熱系數；Tf為表面接觸的介質的溫度；q0為通過表面的熱流密度。

3.2 定子槽處理

電機定子槽內部導線排列不規則，溫度在槽內的分布非常復雜，存在槽滿率、絕緣等問題，因此需對電機定子槽進行簡化分析：假設繞組為均勻分布，將多匝繞組等效為一根導熱體，忽略繞組絕緣漆對溫度的影響，并且假設一根導熱體完全填充定子槽[17-18]。

3.3 接觸面之間對流系數

電機氣隙分別與電機3部分進行接觸，電機氣隙外表面與定子內表面、槽鍥之間，氣隙內表面與轉子之間存在熱量對流傳導，定子外表面與機殼之間存在熱量對流傳導。這3類對流系數對電機溫升計算起重要作用。

氣隙內表面與轉子外表面對流系數：

(11)

式中：v為轉子表面旋轉線速度。

氣隙外表面與定子內表面對流系數：

(12)

假設機殼初始溫度與外界溫度都為初始溫度，定子外表面與機殼對流系數：

(13)

式中：λ0為發熱體在初始溫度中的對流系數;v0為外界空氣流動速度；k為初始溫度空氣流動效率；α為機殼、空氣初始溫度。

如果機殼為自然冷卻，則定子外表面與機殼對流系數：

(14)

4 氣隙流場及電機溫度場分析

4.1 電機氣隙流場分析

本文以一臺24槽，300 kW，18 000 r/min高速永磁同步電機為例，對電機進行流場及溫度場研究，電機模型如圖2所示。

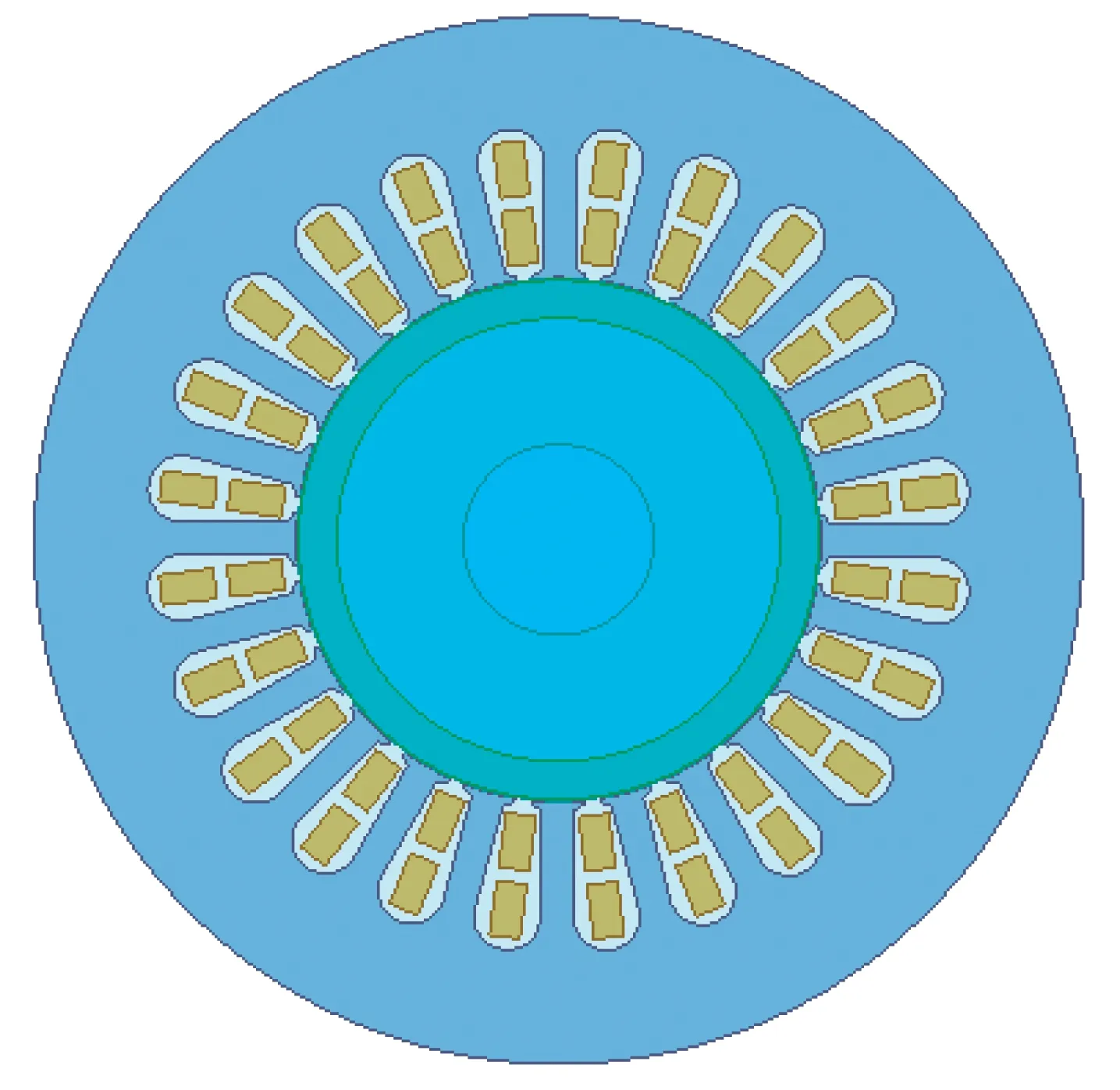
圖2 電機模型

當電機在額定轉速18 000 r/min下運行時，根據流場模型，由ANSYS Fluent有限元分析得到電機氣隙的空氣流動速度，如圖3所示。

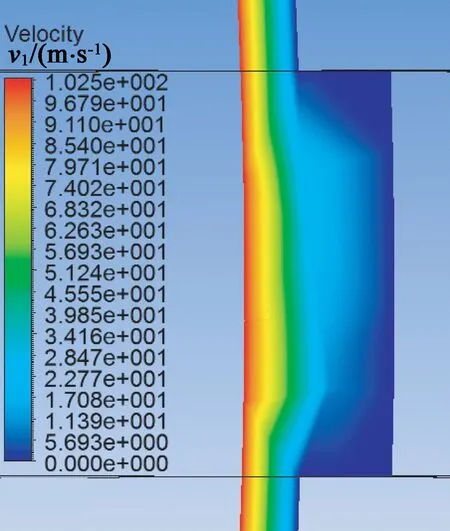
圖3 額定轉速18 000 r/min氣隙線速度

由圖3得到，空氣與轉子交界面處的空氣流動速度最大，為102.5 m/s，定子表面線速度為0，根據計算轉子線速度為102.7 m/s，可見ANSYS Fluent仿真結果具有準確性。仿真得到氣隙流動速度小于計算結果原因是，定轉子表面非絕對光滑，存在不同程度的粗糙度，會延緩空氣流動速度。

空氣平均速度：

(15)

根據經驗，一般將電機氣隙中空氣的流動速度等效為轉子旋轉線速度的一半。在高速電機中，可見這種考慮方式并不適合，空氣平均旋轉速度稍大于線速度的一半。

由Fluent模擬電機在額定轉速情況下氣隙摩擦生熱得到如圖4所示的電機氣隙內溫度梯度的變化。

圖4 額定轉速下氣隙摩擦溫度

由Fluent對不同轉速情況下氣隙內溫度分布情況進行分析，可得到電機定子內表面、轉子外表面及氣隙中部溫度值，如表1所示。

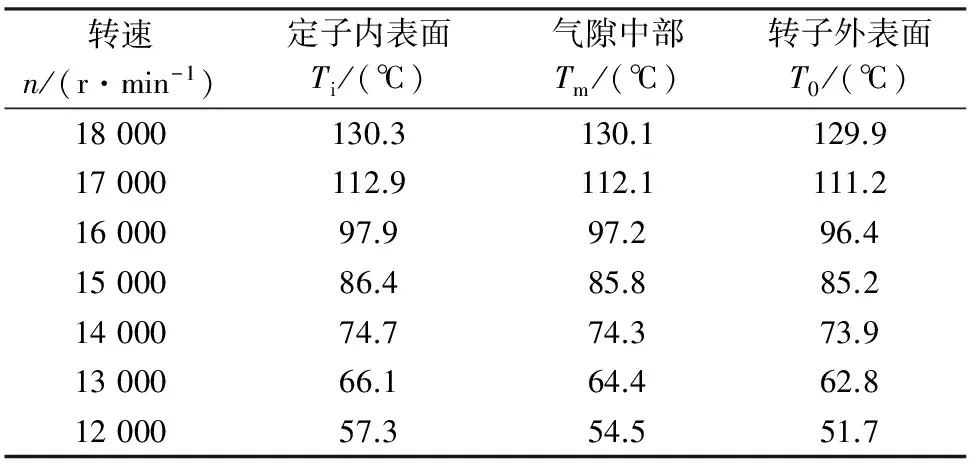
表1 不同轉速電機氣隙溫度

定子內表面的粗糙度大于轉子外表面粗糙度，因此定子內表面溫度值略高于轉子外表面。

4.2 電機氣隙溫度場分析

根據電機溫度場模型，將氣隙與定轉子之間的對流系數及表1中氣隙空氣摩擦引起的溫度變化，加載到溫度場求解域上得到電機溫升分布情況，如圖5所示。

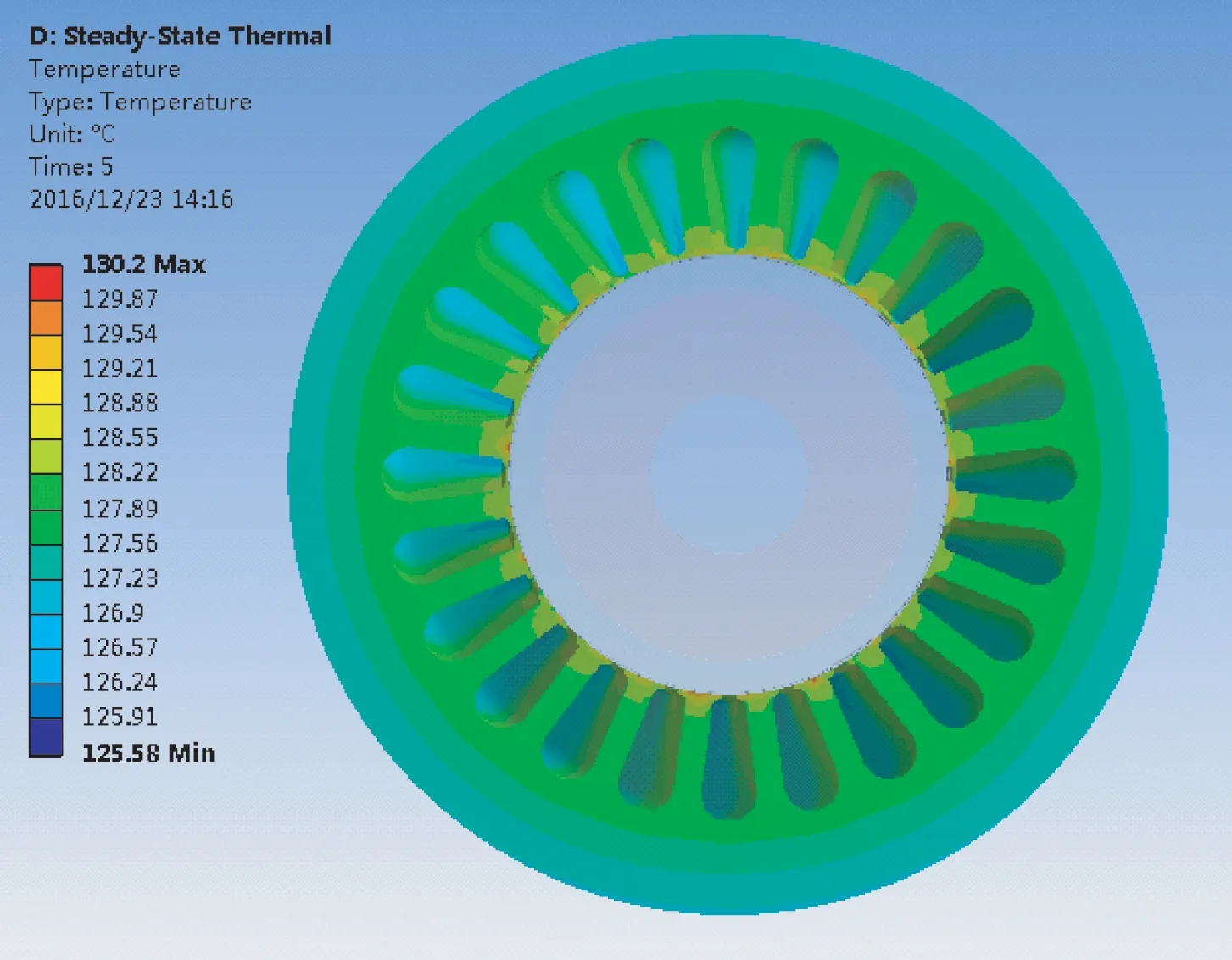
(a) 電機定子溫度場

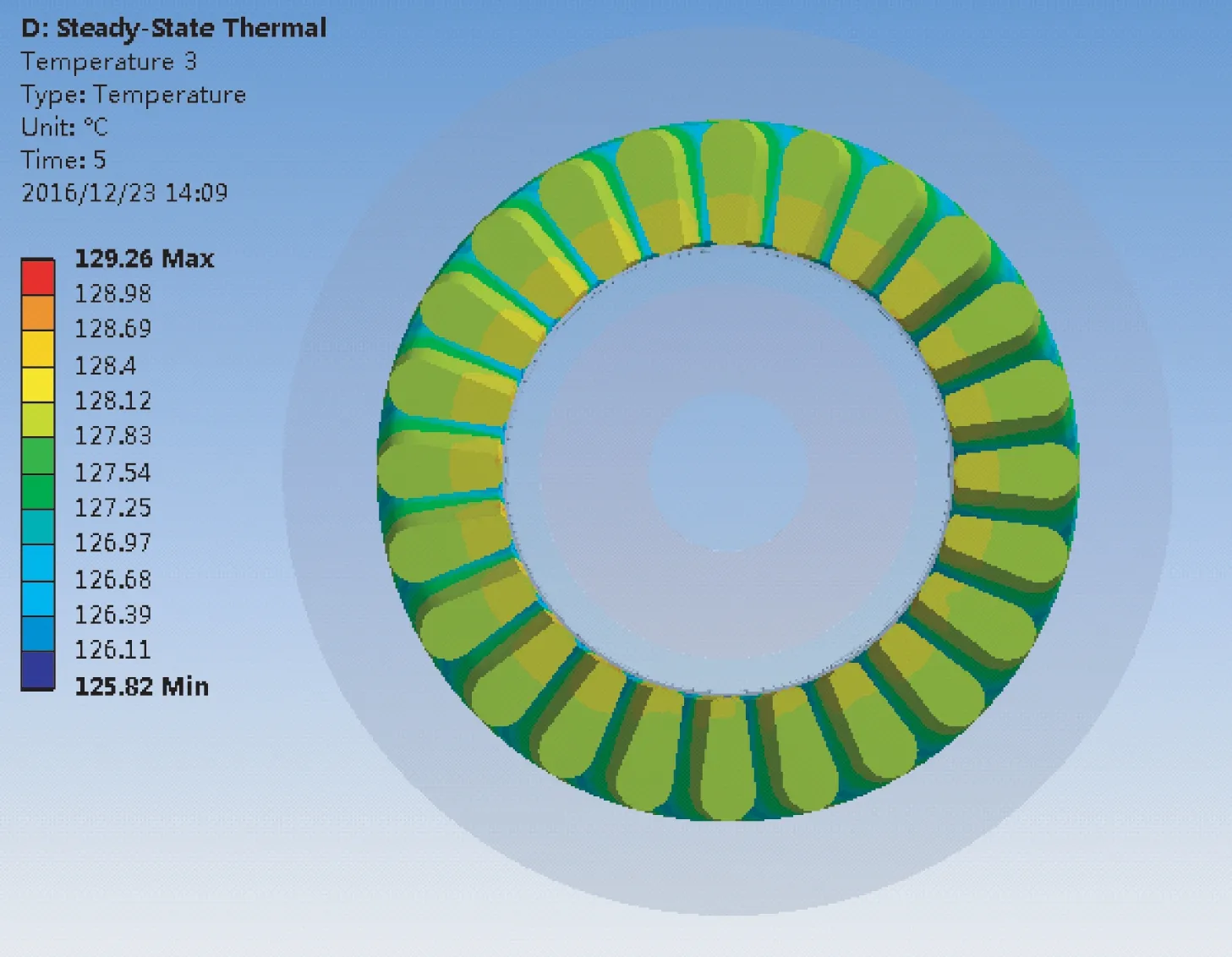
(b) 電機繞組溫度場

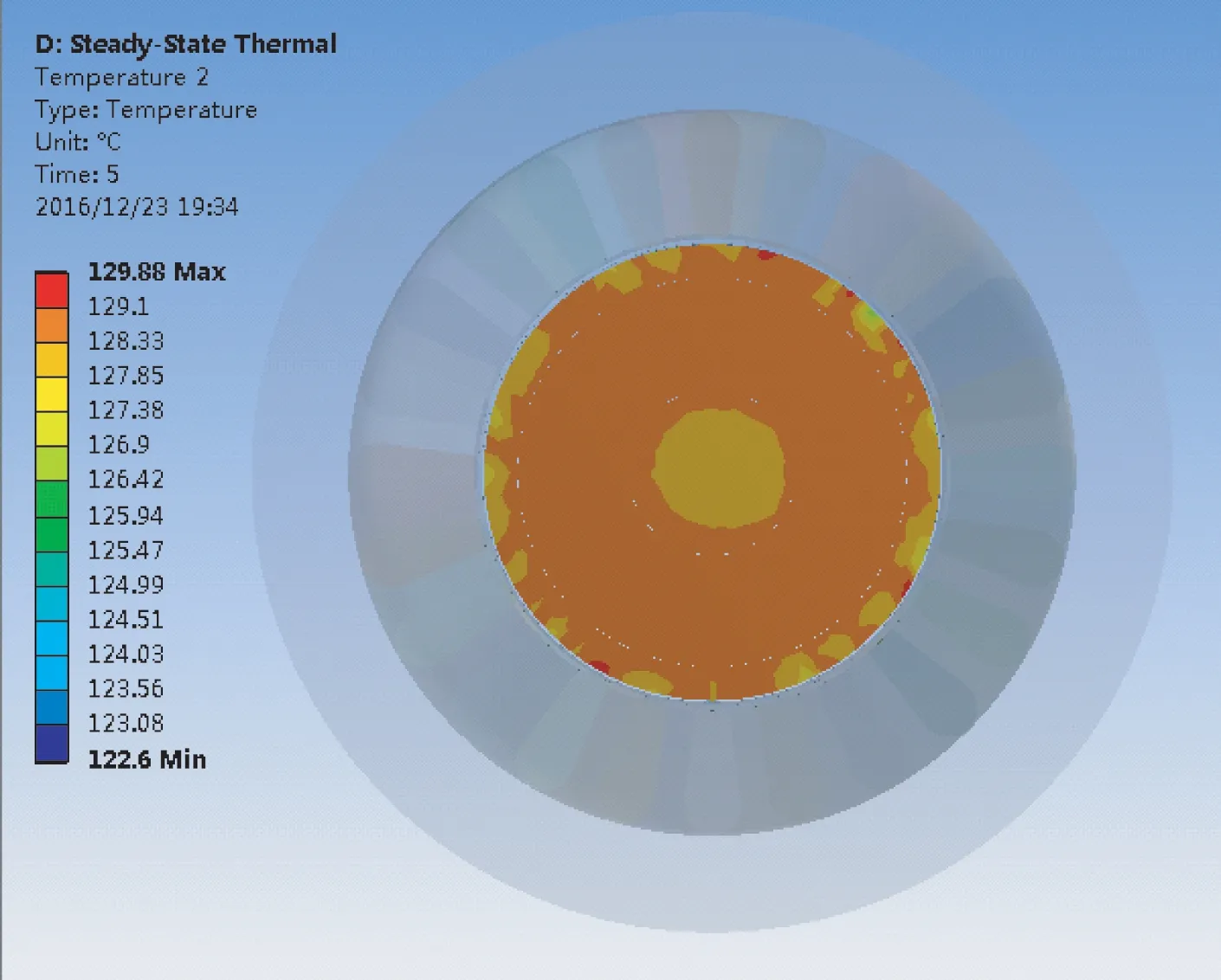
(c) 電機轉子溫度場

由以上仿真結果得出，電機在額定轉速運行時氣隙摩擦對定轉子、繞組的溫度分布的影響。最高溫度主要集中在定子與氣隙接觸部分，原因在于定子表面粗糙程度大于轉子表面粗糙程度，從而使氣隙與定子摩擦產生更多熱量。由于定子外表面與機殼存在熱傳導，因此，定子外表面溫度最低。轉子表面溫度接近130 ℃，對永磁體而言，該溫度不可忽視。

分析電機在不同轉速下氣隙摩擦生熱對定轉子、繞組溫度場分布的影響，如圖6所示。

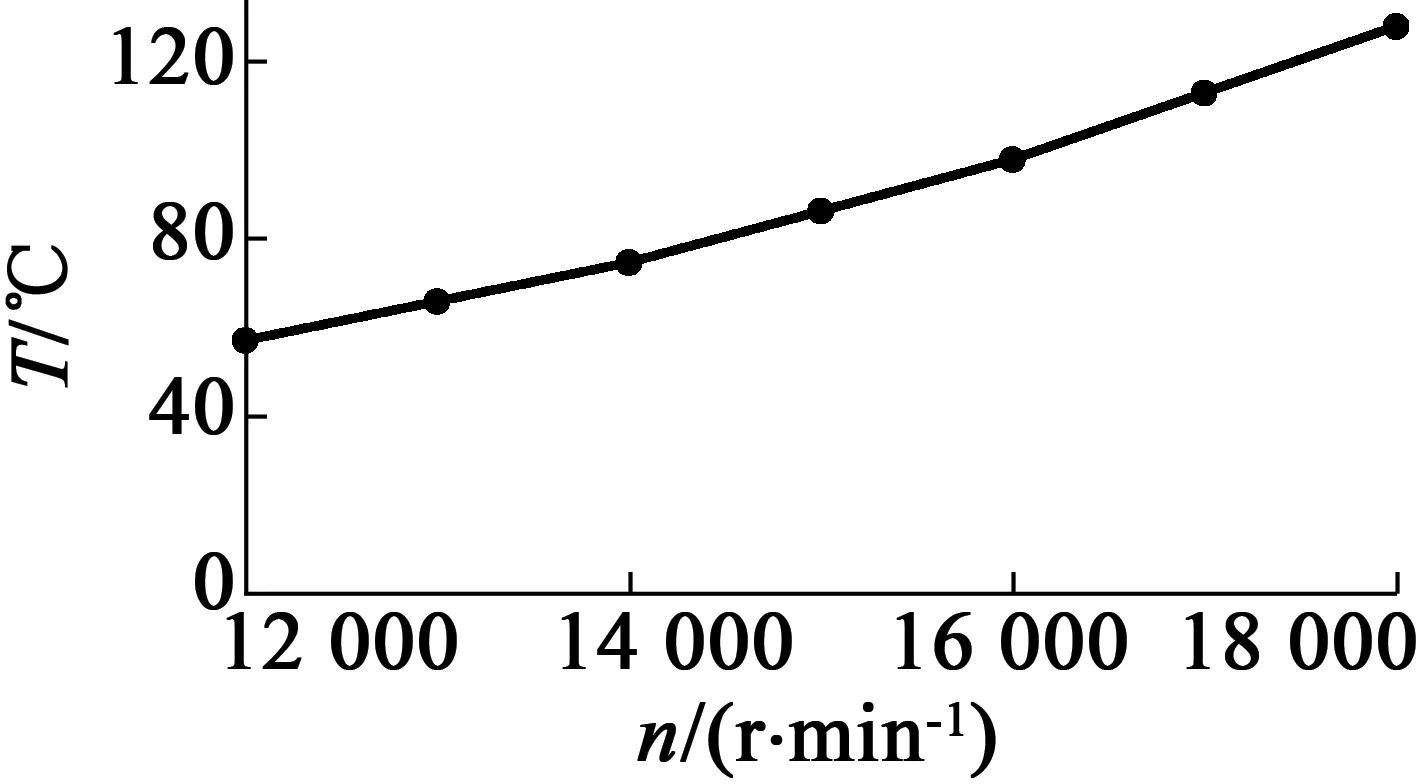
(a) 定子溫度變化

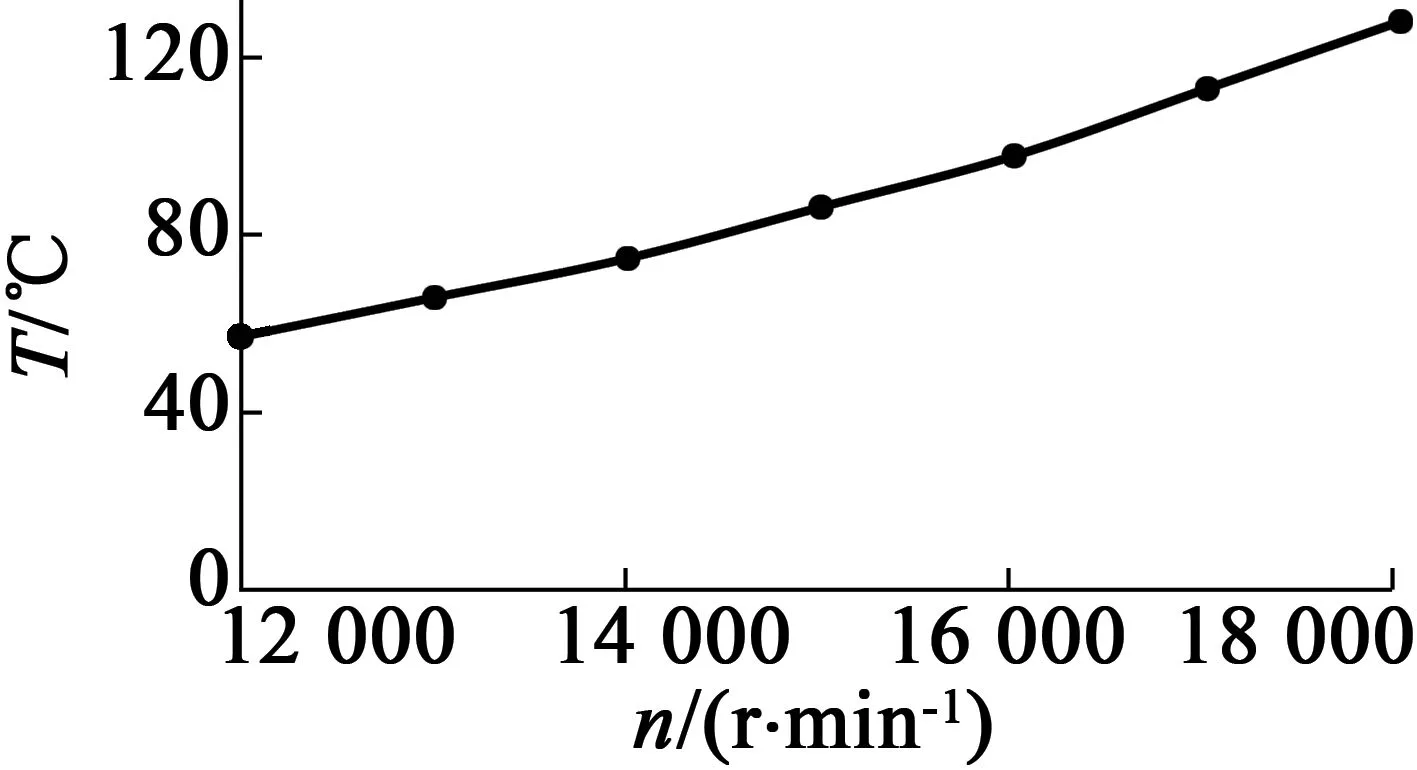
(b) 繞組溫度變化

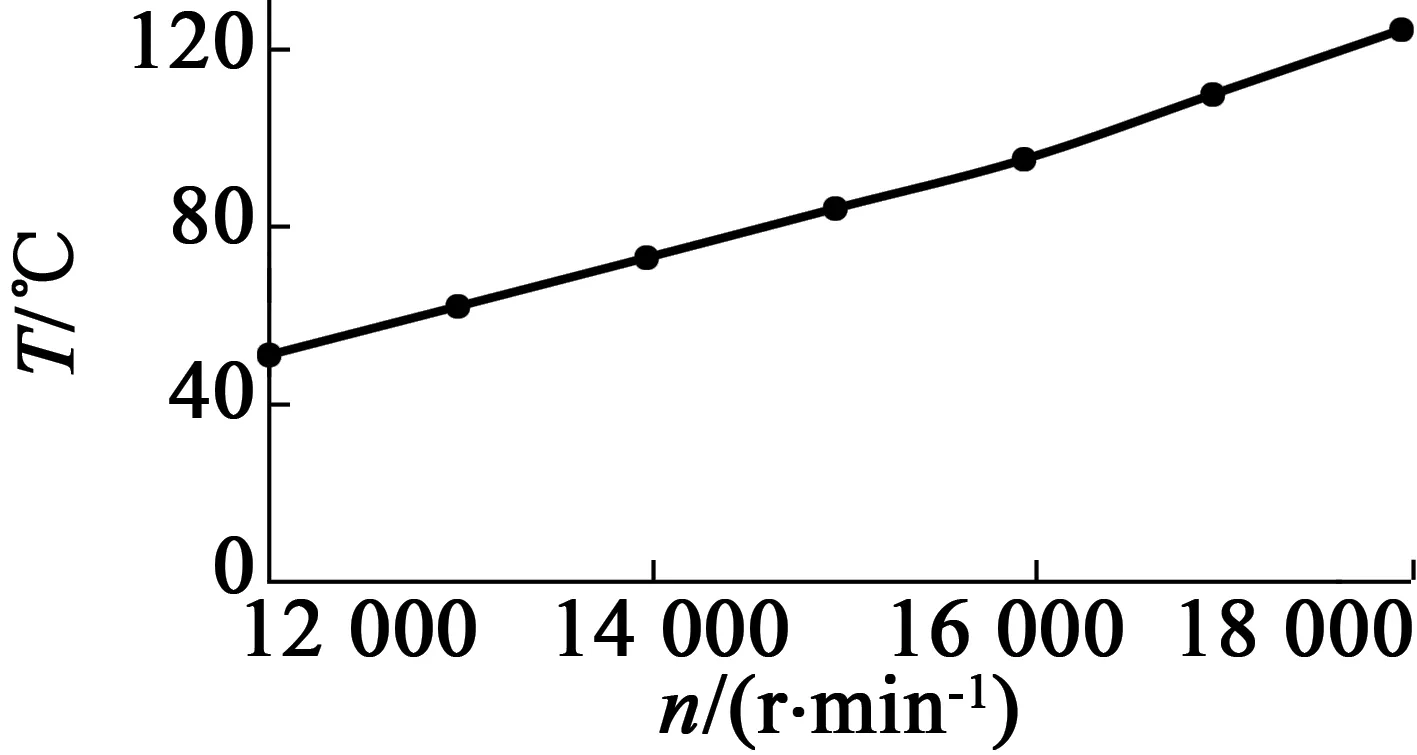
(c) 轉子溫度變化

由以上數據可以看出，隨著轉速的增大，定子、轉子以及繞組溫升逐漸增大，當轉速達到額定轉速18 000 r/min時，定轉子、繞組溫度達到最大值，為127.893 ℃，對于對溫度比較敏感的永磁體而言，氣隙摩擦引起的溫升不容忽視。

5 結 語

本文利用ANSYS Fluent對高速電機氣隙流場進行分析，得出的計算電機氣隙流速為轉子外表面線速度的一半的，在高速電機中并不適用。在高速電機中，氣隙空氣旋轉速度要稍大于轉子線速度的一半。利用ANSYS對高速電機溫度場進行分析，得出氣隙摩擦生熱對定轉子、繞組溫度分布影響十分明顯，在電機溫度場計算中所占比重較大，特別是對于溫度較為敏感的永磁體而言，氣隙摩擦引起的溫升不容忽視。

[1] 周鳳爭,沈建新,王凱.轉子結構對高速無刷電機轉子渦流損耗的影響[J].浙江大學學報工學版,2008,42(9):1587-1590.

[2] AGLEN O.Loss calculation and thermal analysis of a high-speed generator[C]//2003.IEEE International Electric Machines and Drives Conference.IEEE,2003(2):1117-1123.

[3] WANG F,ZONG M,ZHENG W,et al.Design features of high speed PM machines[C]//International conference on machine and system.2003(1):66-70.

[4] 楊平西,張福清,許承千.船用隱極無刷發電機混合通風和溫度場仿真計算研究[J].船舶工程,2001(6):32-35.

[5] 江有名,丁樹業,葛云中.大容量風力發電機內流體場及溫度場的數值分析[J].大功率變流技術,2010(4):24-27.

[6] 羅慧強.風力發電機的流體場和溫度場數值分析[D].成都:西南交通大學,2012:42-44 .

[7] SHANEL M,PICKERING,et al.Application of computational fluid dynamics to the cooling of salient pole electrical machines[C]//2000:338-342.

[8] AIROLDI G,BUMBY J R,DOMINY C,et al.Air flow and heat transfer modeling of an axial flux permanent magnet generator[J].World Academy of Science Engineering & Technology,2009(58).

[9] 胡坤,李振北.ANSYS ICEM CFD工程實例詳解[M].北京:人民郵電出版社,2014.

[10] 高思煜,丁輝,程凱,等.高速電主軸內置電機空氣摩擦損耗研究[J].電機與控制應用,2014(10):20-25.

[11] 丁欣碩,焦楠.FLUENT14.5流體仿真計算從入門到精通[M].北京,清華大學出版社,2014.

[12] 孫芝茵.高速永磁同步電機損耗及熱特性的研究[D].哈爾濱:哈爾濱工業大學,2011.

[13] 邢軍強,王鳳翔,張殿海,等.高速永磁電機轉子空氣摩擦損耗研究[J].中國電機工程學報,2010(27):14-19.

[14] 韋敏,賈惠芹.一種小功率無刷直流電動機的數字化控制系統設計[J].西安石油大學學報(自然科學版),2011,26(1):76-78.

[15] 周鳳爭,沈建新,王凱,等.帶正反轉功能的通用型無刷直流電機控制器設計[J].微電機,2007,40(10):43-44.

[16] 魏雪環,蘭志勇,謝先銘,等.永磁體渦流損耗與永磁同步電機溫度場研究[J].電機與控制應用,2015(5):28-31.

[17] 王北社,竇滿鋒.基于熱網絡法的高功率密度異步電動機定子溫升計算[J].微特電機,2006,34(11):24-26.

[18] 鮑里先科,魏書慈,邱建甫.電機中的空氣動力學與熱傳遞[M].北京:機械工業出版社,1985.