基于二階滑模算法的永磁同步電機控制

楊 婧，紀科輝，趙新龍，魯文其

(浙江理工大學，杭州 310018)

0 引 言

永磁同步電機在運動控制領域中占據著主導地位，如何準確地測量電機的速度是精確控制的前提。電機控制中最經典的是比例積分微分調節(以下簡稱PID)控制，由于PID控制器結構簡單、容易數字實現等優點，使用廣泛。單純的PID控制系統參數依賴性強，魯棒性差，抗負載擾動能力很有限，降低了系統的控制性能，因此很難滿足高精度伺服控制系統的要求[1]。

為了提高電機的控制性能，使得電機在實際控制中獲得良好的動態響應，學者針對上述問題提出了一些魯棒控制方法，如神經網絡控制、非線性控制、模糊控制、自適應控制和滑模控制等[2]。

滑模控制因具有對永磁同步電機系統參數時變和對外部干擾的強魯棒性，成為國內外學者研究的熱點領域[3]。傳統的一階滑模控制存在一些不可忽視的缺點。由于控制過程中的不連續性，系統在運行過程中容易引起抖振，而抖振將嚴重影響伺服系統的準確度和穩定度[4-5]。研究表明，在準確設計和調節滑模參數的前提下，滑模觀測器能夠較為準確地估計系統的參數[6-7]。

本文針對如何提高電機系統的動態性能的問題，提出了一種電機速度的二階滑模算法。算法不僅保留了滑模控制的優點，并且能夠從根本上消除抖振現象。該算法通過對實際位置信號的檢測，來計算實際速度值，從而實現對電機轉速的反饋調節。

1 滑模算法的原理

考慮一個動態系統：

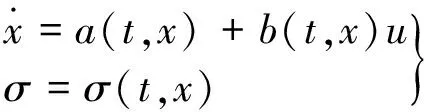
(1)

式中：x∈Rn為狀態變量(Rn為n維實數空間);u∈R為控制函數的輸入(R為實數集);a(t,x)，b(t,x)為不確定的光滑函數;σ(t,x)為輸出函數，σ和n是未知的。假設該系統的相對度為2，為使輸出σ在有限時間消失，并且通過一種不連續的全局有界反饋控制來保持σ≡0，系統的軌跡應該在任何有限輸入時間內被無限延伸[8]。

(2)

式中：函數h(t,x)，g(t,x)為未知的光滑函數。由于控制函數u有界并且連續，假設輸入輸出條件如下：

(3)

式中：C，Km，KM∈R+(R+為正實數集)。

在設定的有限區間內，由式(2)和式(3)得到：

(4)

設定反饋函數：

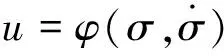
(5)

2 二階滑模算法的設計

二階滑模方法可以應用于永磁同步電機速度的計算[9-10]，根據上節所述的二階滑模算法提出了一種具有微分結構的二階滑模速度計算方法。

二階滑模的微分算法計算框圖如圖1所示。

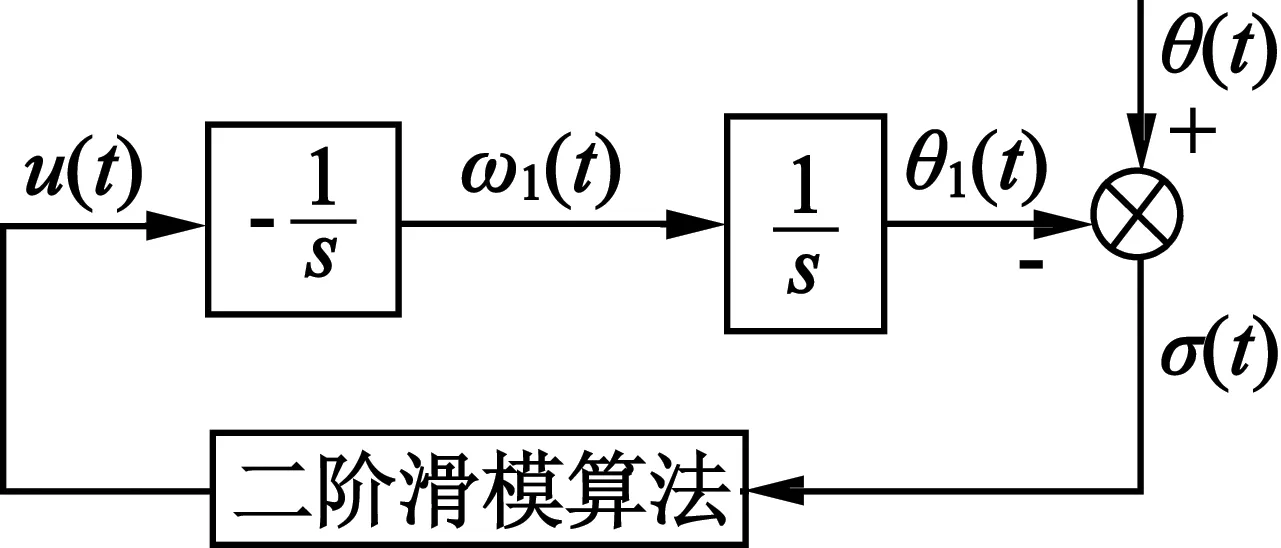
圖1 二階滑模算法

積分器的輸出信號θ1(t)和ω1(t)，分別跟蹤輸入信號θ(t)和它的微分信號，驅動信號u(t)是數字控制的分段恒定輸出。設a[k]=a(kT)表示一個通用信號a(t)在采樣時刻t=kT的采樣值，k=0,1,2,…，其中T為采樣周期。

(6)

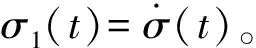
(7)

如果一個正常數X2是已知的：

(8)

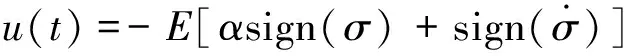
(9)

式中：E，α為滑模控制函數的增益。

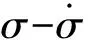
根據式(6)和式(7)，可得電機加速度u(t)和轉速ω1(t)的計算框圖，如圖2所示。

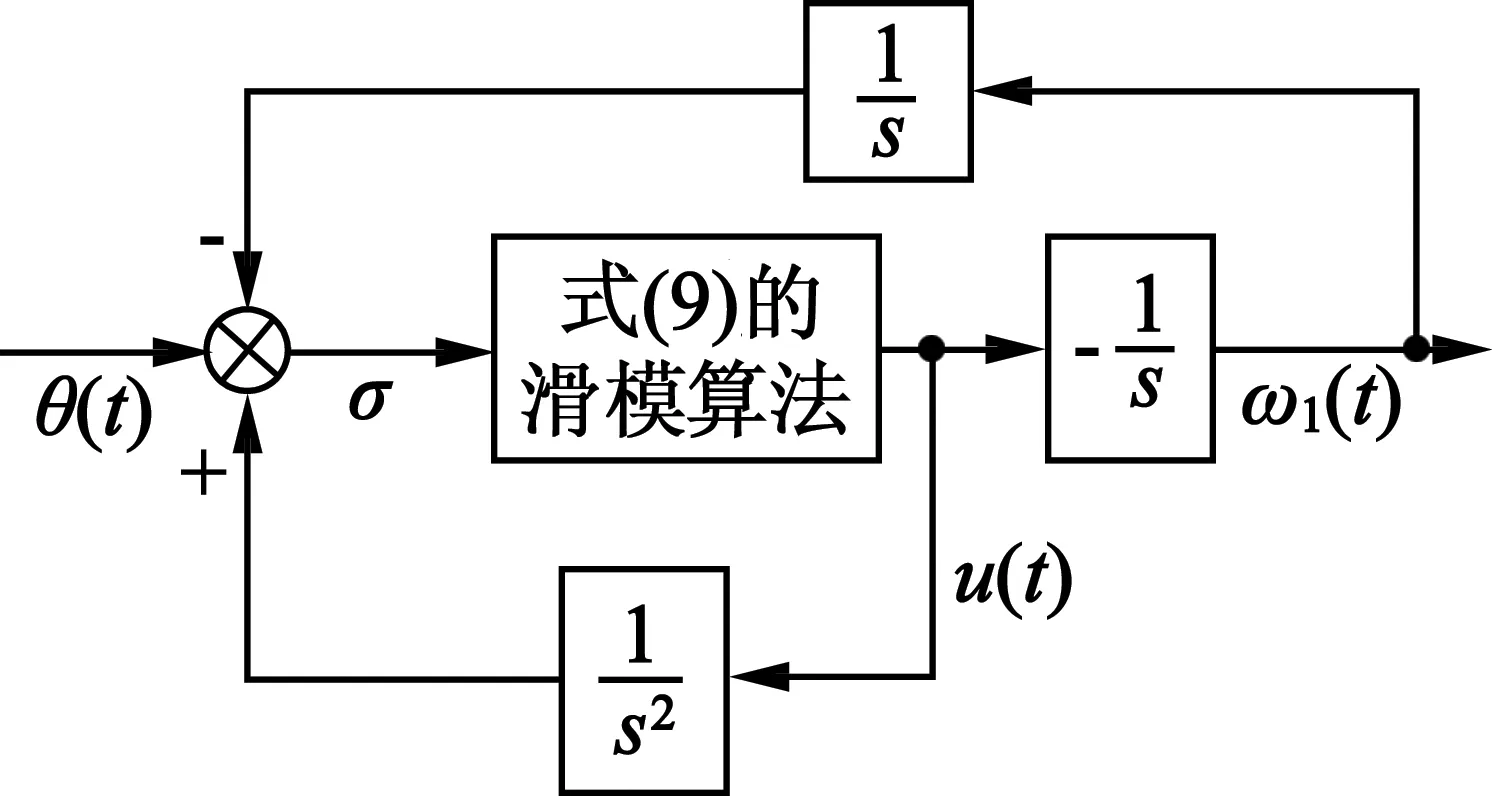
圖2 電機加速度和速度的計算

3 仿真結果與分析

傳統的永磁電機驅動器采用的是PI閉環控制，速度由位置信號直接微分得到。但是由于在電機的實際系統運行過程中，其負載經常受到外界擾動，負載擾動會影響系統的動態性能。為使伺服系統具有良好的魯棒性和速度跟蹤性能，必須克服負載擾動對電機轉速的影響。

本文在傳統PI閉環控制模型的基礎上加上二階滑模速度計算模塊，如圖3所示。

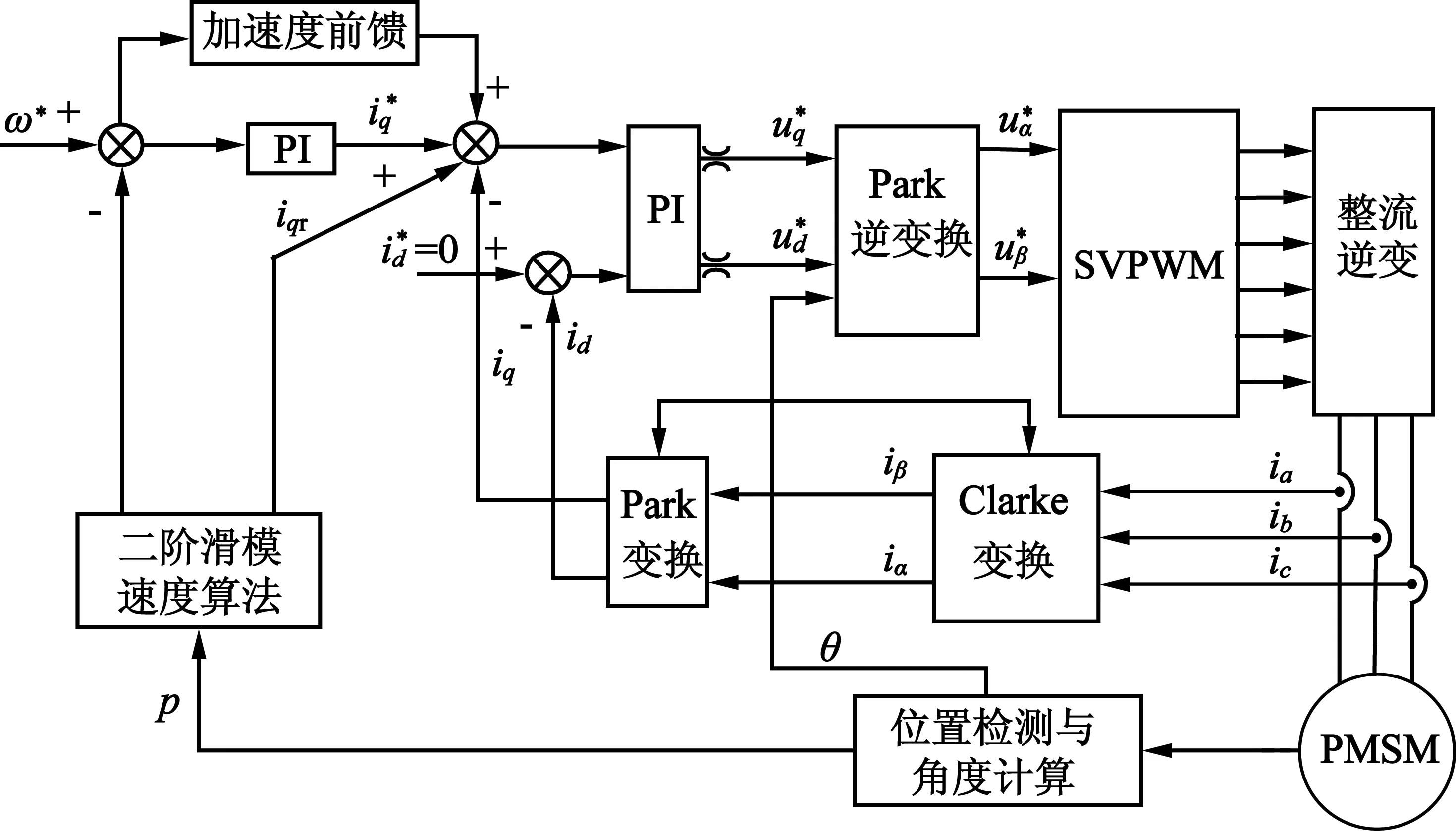
圖3 基于二階滑模算法的電機驅動系統

通過編碼器對位置信號的追蹤，對實際位置信號進行二階滑模運算，得出速度值和負載轉矩估計值，通過速度負反饋控制對給定速度進行調節。

用MATLAB環境下的仿真軟件Simulink對上述采用二階滑模算法控制的電機驅動系統進行仿真。仿真電機參數如下：R=2.875 Ω，Ld=Lq=8.5 mH，J=0.8×10-3kg·m2，μ=0.02 N·m·s。

圖4(a)為當給定速度為1 000 r/min時采用傳統的速度計算方法空載起動時速度的響應。由圖4(a)可知，在空載起動時，采用傳統的差分算法的系統電機起動時速度的上升時間為10.3 ms，超調量為8.6%，穩態誤差為27.5～29.5 r/min。圖4(b)為當給定速度為1 000 r/min時采用二階滑模算法空載起動時速度的響應。由圖4(b)可知，在空載起動時，采用二階滑模算法的系統,電機起動時速度的上升時間為7.33 ms，幾乎沒有超調量，穩態誤差也很小。圖5為采用二階滑模算法時的空載起動速度響應局部放大。由圖5可知，采用二階滑模算法的系統電機速度的穩態誤差為17.9～21.5 r/min。

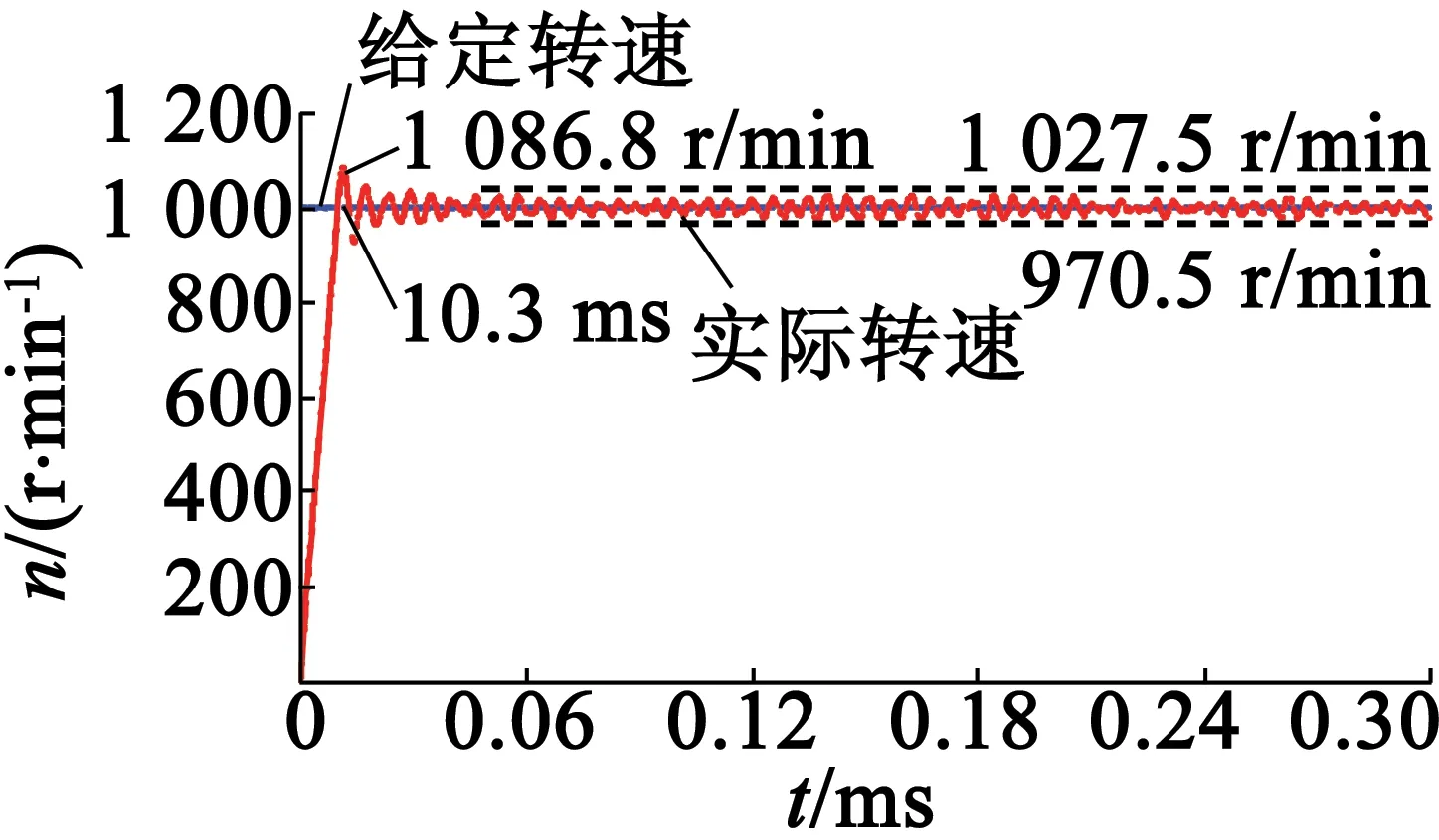
(a) 傳統的速度計算方法

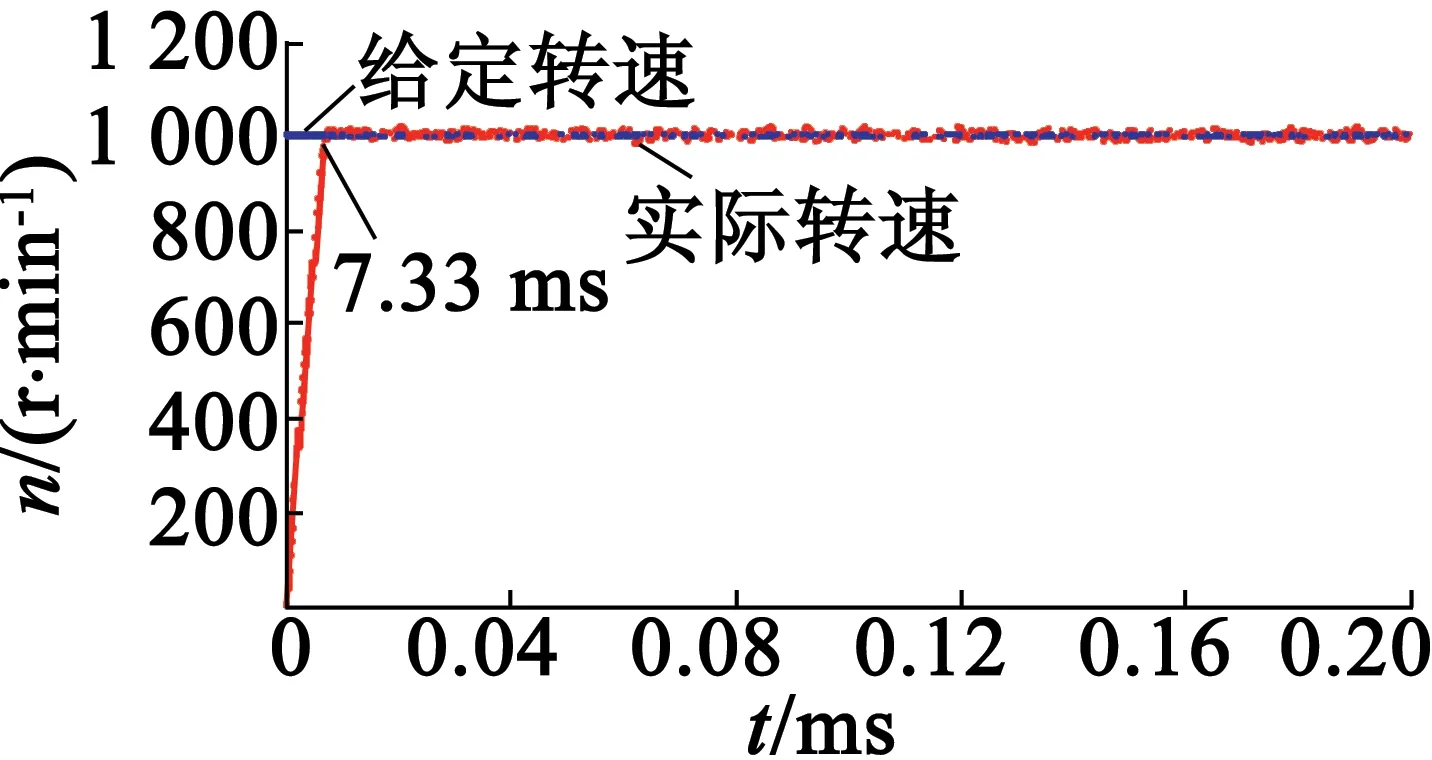
(b)二階滑模算法

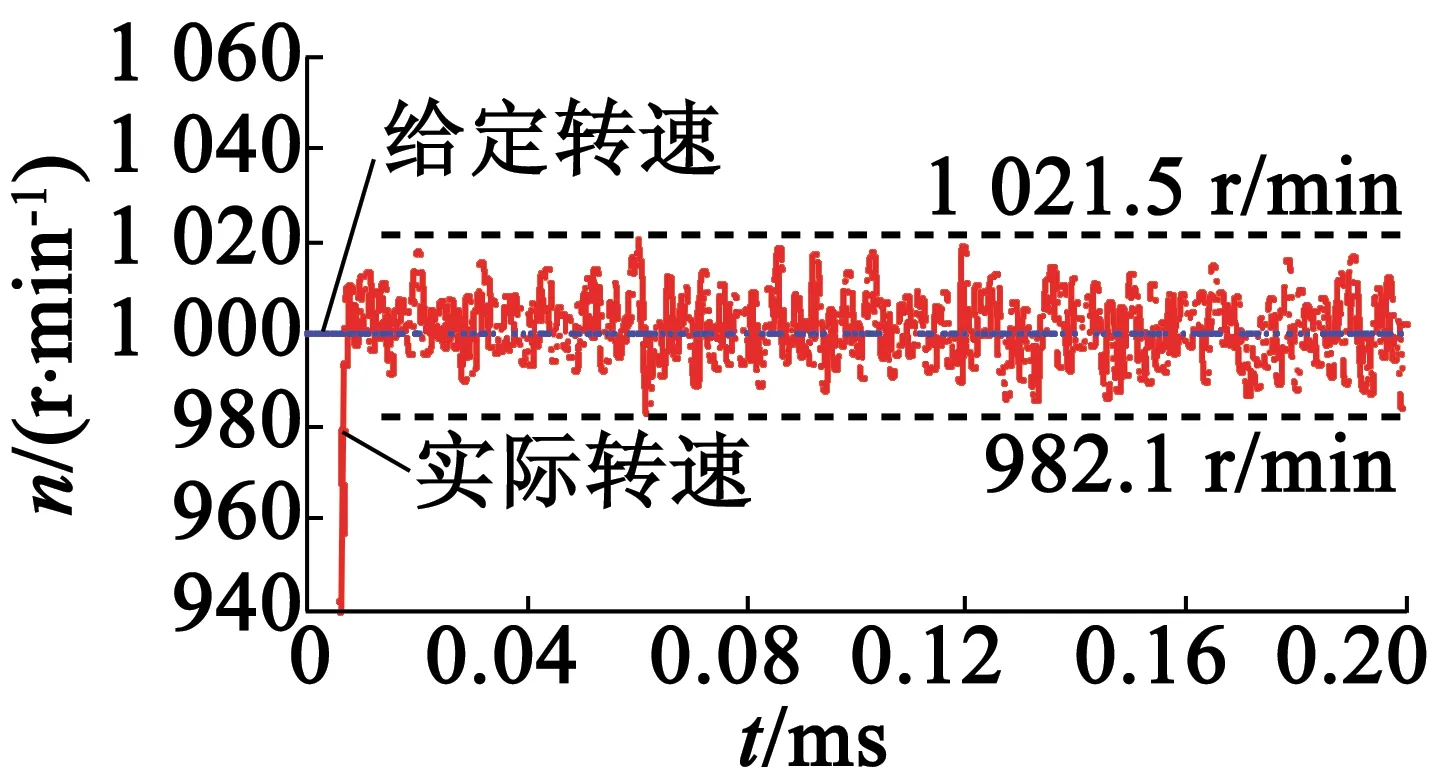
圖5 采用二階滑模算法時的空載起動速度響應局部放大

由上述數據可以明顯看出，傳統的電機系統波形上升時間較大，超調量較大，電機起動時間較長，穩態誤差較大；而加滑模后的波形上升時間縮短，超調量變小，電機的起動時間明顯縮短，穩態誤差較小。這就驗證了采用二階滑模算法的交流伺服系統具有良好的魯棒性。

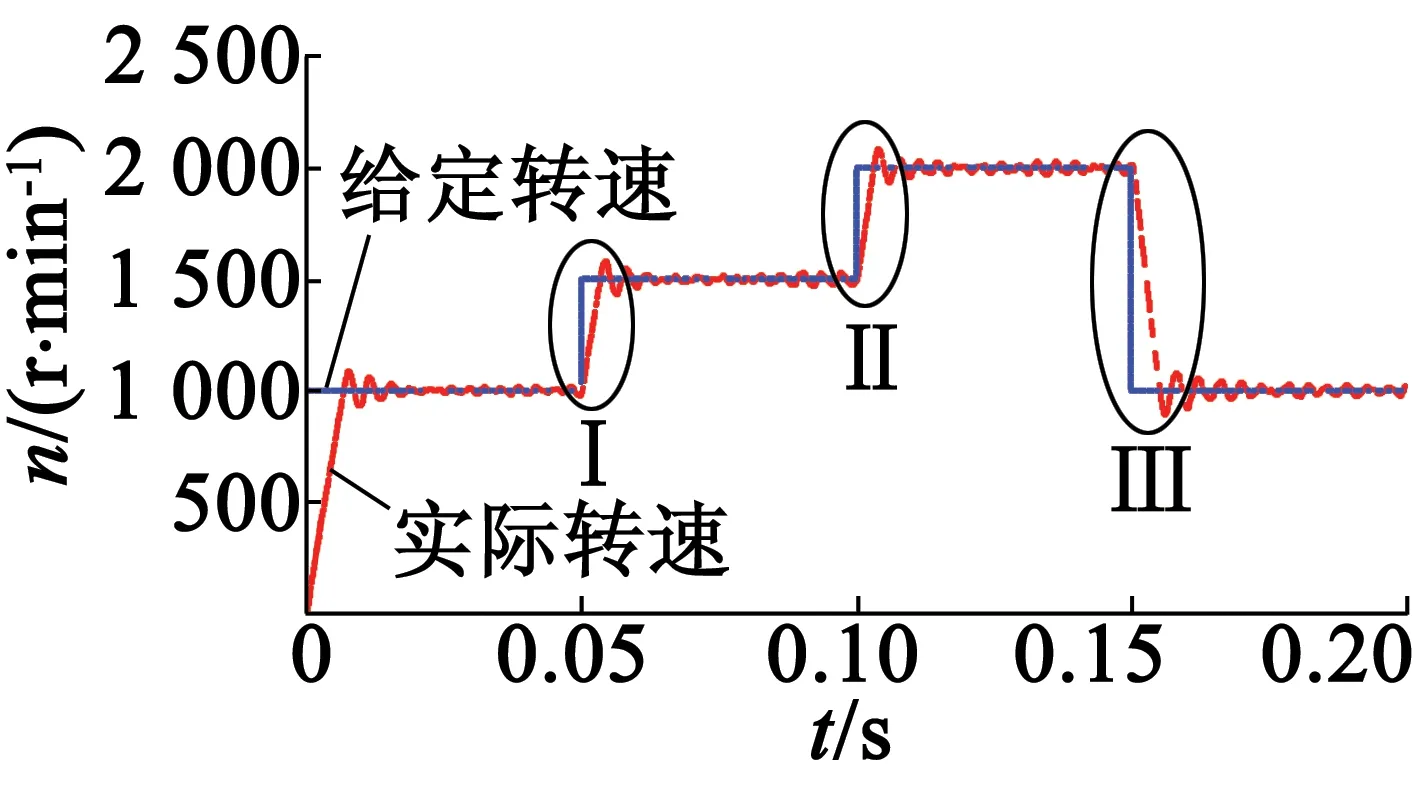
圖6 采用傳統的速度計算方法的響應速度

圖6為當系統給定速度為階躍信號時采用傳統的速度計算方法的響應速度。由圖6可知，系統速度給定值從1 000 r/min至2 000 r/min的階躍信號。在0.05s時，給定速度由1000r/min上升至1 500 r/min;在0.1 s時，給定速度由1 500 r/min上升至2 000r/min;在0.15s時，給定速度由2000r/min下降至1 000 r/min,電機的速度隨著系統給定的速度的改變而改變。圖7為采用傳統的速度計算方法的響應速度的局部放大。由圖7(a)可知，當電機速度由1 000 r/min上升至1 500 r/min時，所需時間為3.7ms，達到1 500r/min時的穩態誤差為18.5～52.5 r/min。由圖7(b)可知，當電機速度由1 500 r/min上升至2 000 r/min時，所需時間為3.5 ms，達到2 000 r/min時的穩態誤差為22～22.9 r/min。由圖7(c)可知，當電機速度由2000r/min下降至1 000 r/min時，所需時間為5.5 ms，達到1 000 r/min時的穩態誤差為28.8～42.6 r/min。

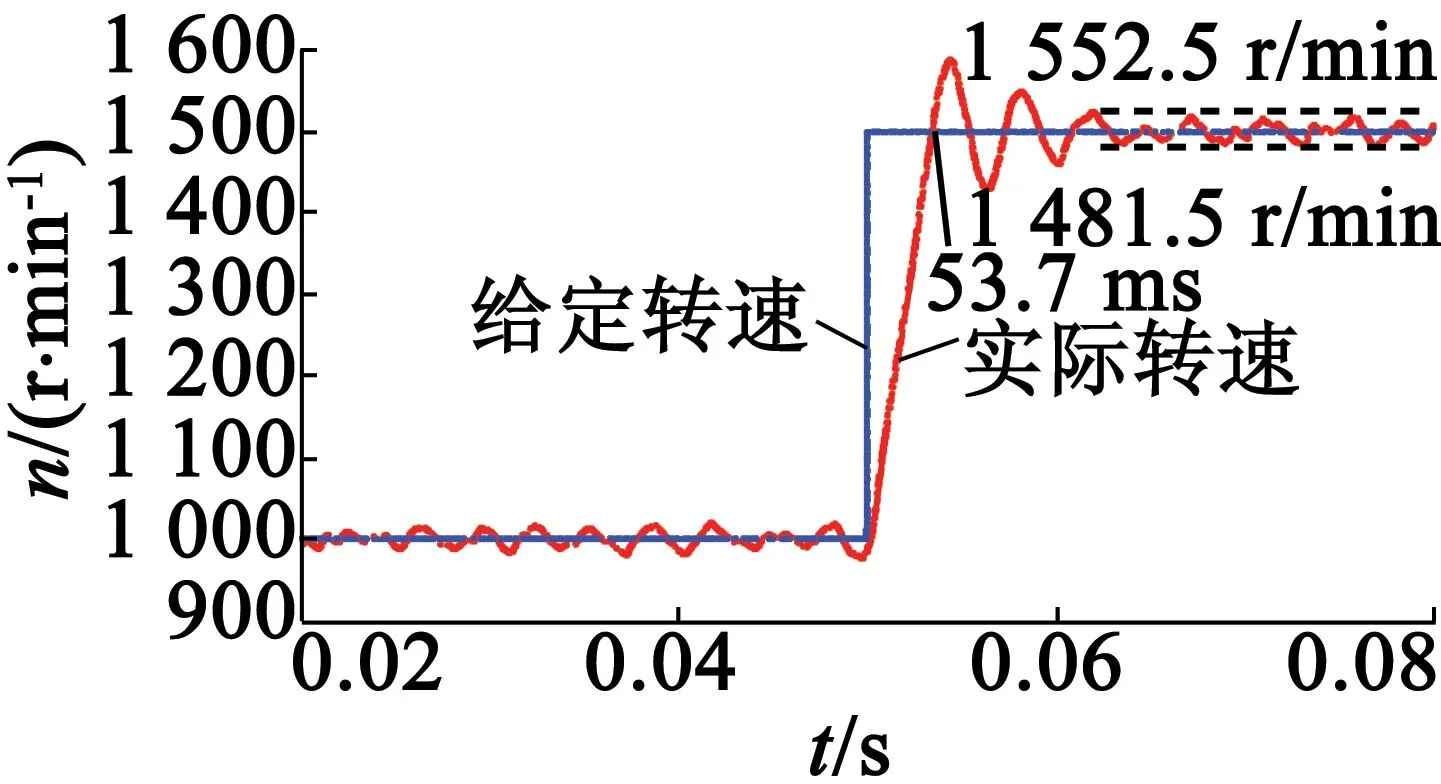
(a)1 000 r/min～1 500 r/min

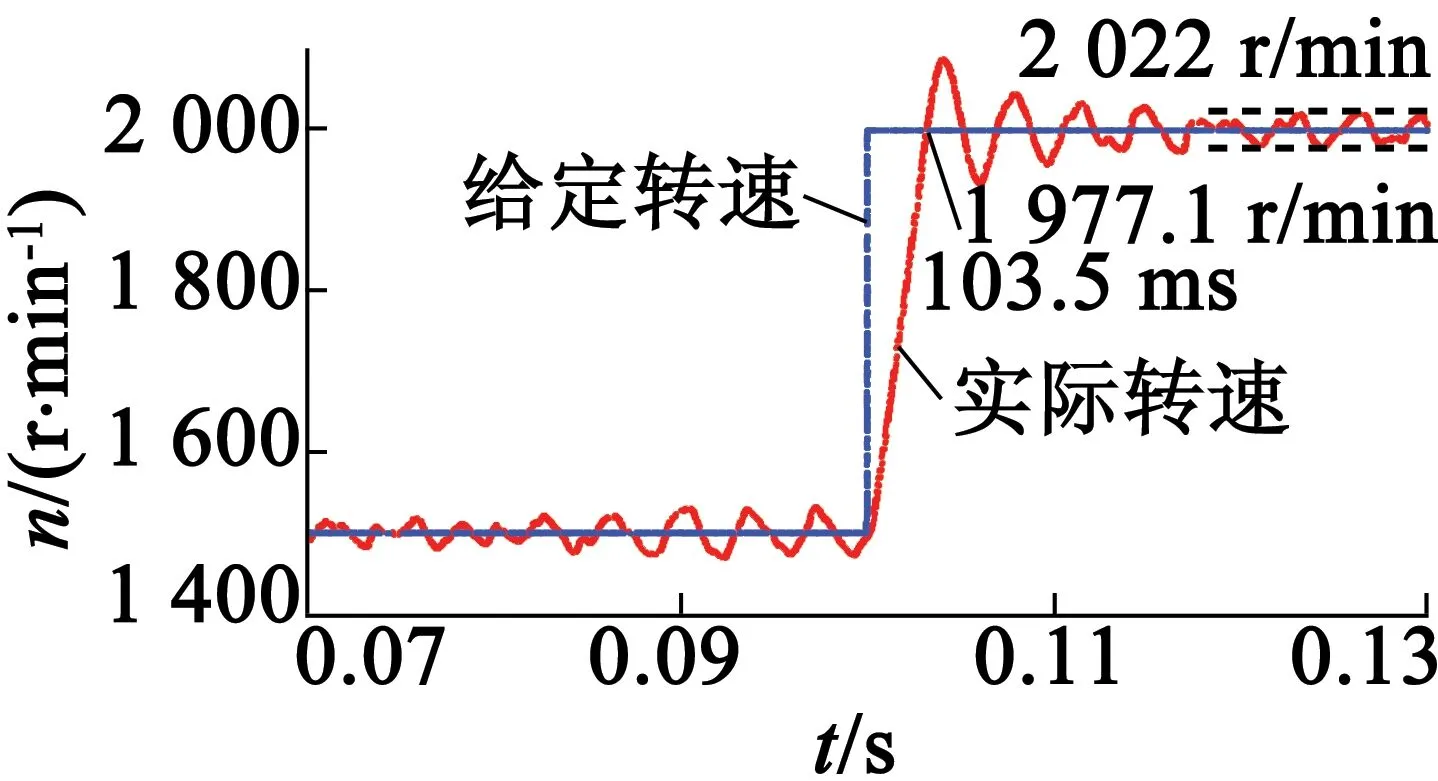
(b)1 500 r/min～2 000 r/min

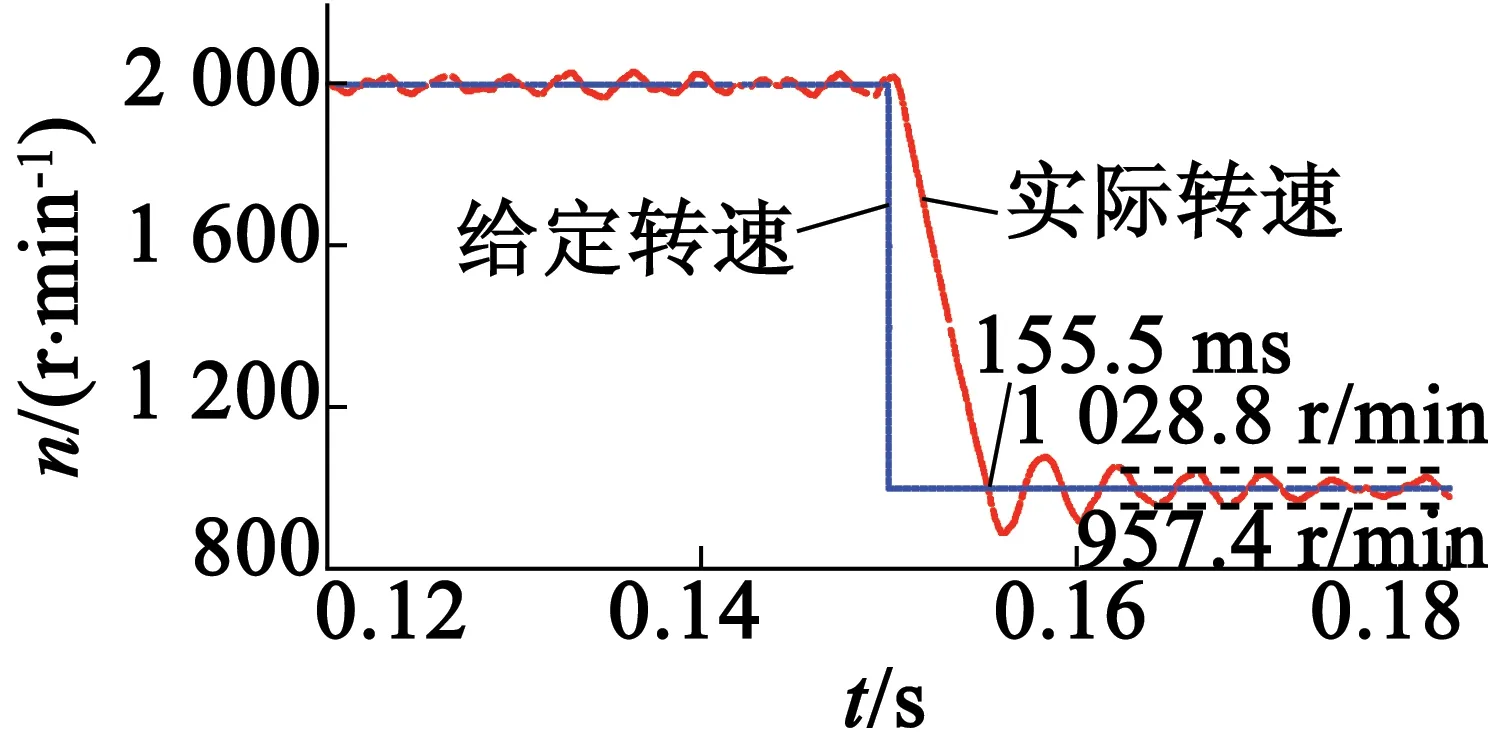
(c)2 000 r/min～1 000 r/min

圖8為當系統給定速度為階躍信號時采用二階滑模算法的響應速度。由圖8可知，電機的速度隨著系統給定的速度的改變而變。圖9為采用二階滑模算法的響應速度的局部放大。由圖9(a)可知，當電機速度由1 000 r/min上升至1 500 r/min時，所需時間為3.4 ms，達到1 500 r/min時的穩態誤差為5.1～44.8 r/min。由圖9(b)可知，當電機速度由1500r/min上升至2000r/min時，所需時間為3.3ms，達到2 000 r/min時的穩態誤差為14.5～17.8 r/min。由圖9(c)可知，當電機速度由2 000 r/min下降至1 000 r/min時，所需時間為5.7 ms，達到1 000 r/min時的穩態誤差為12.9～17.6 r/min。

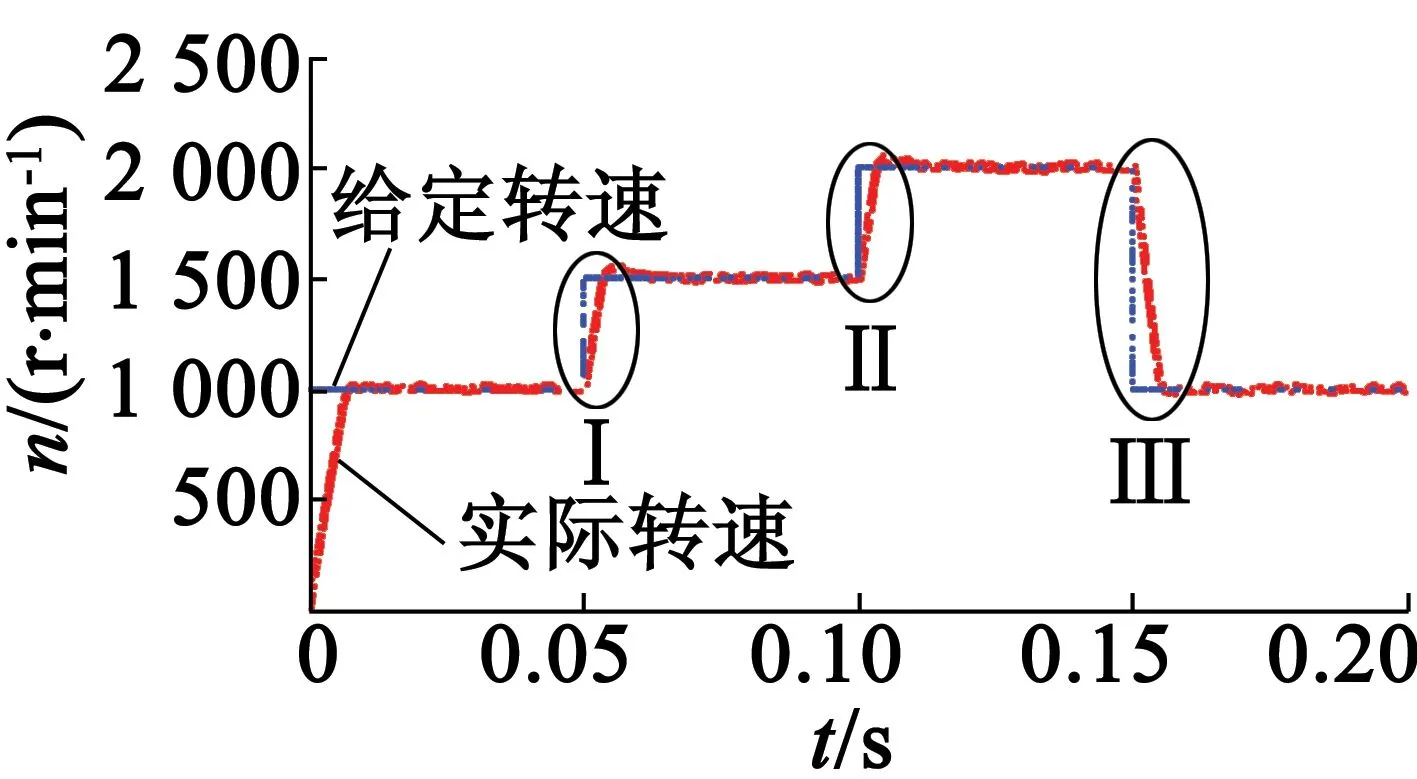
圖8 采用二階滑模算法的響應速度

(a)1 000 r/min～1 500 r/min

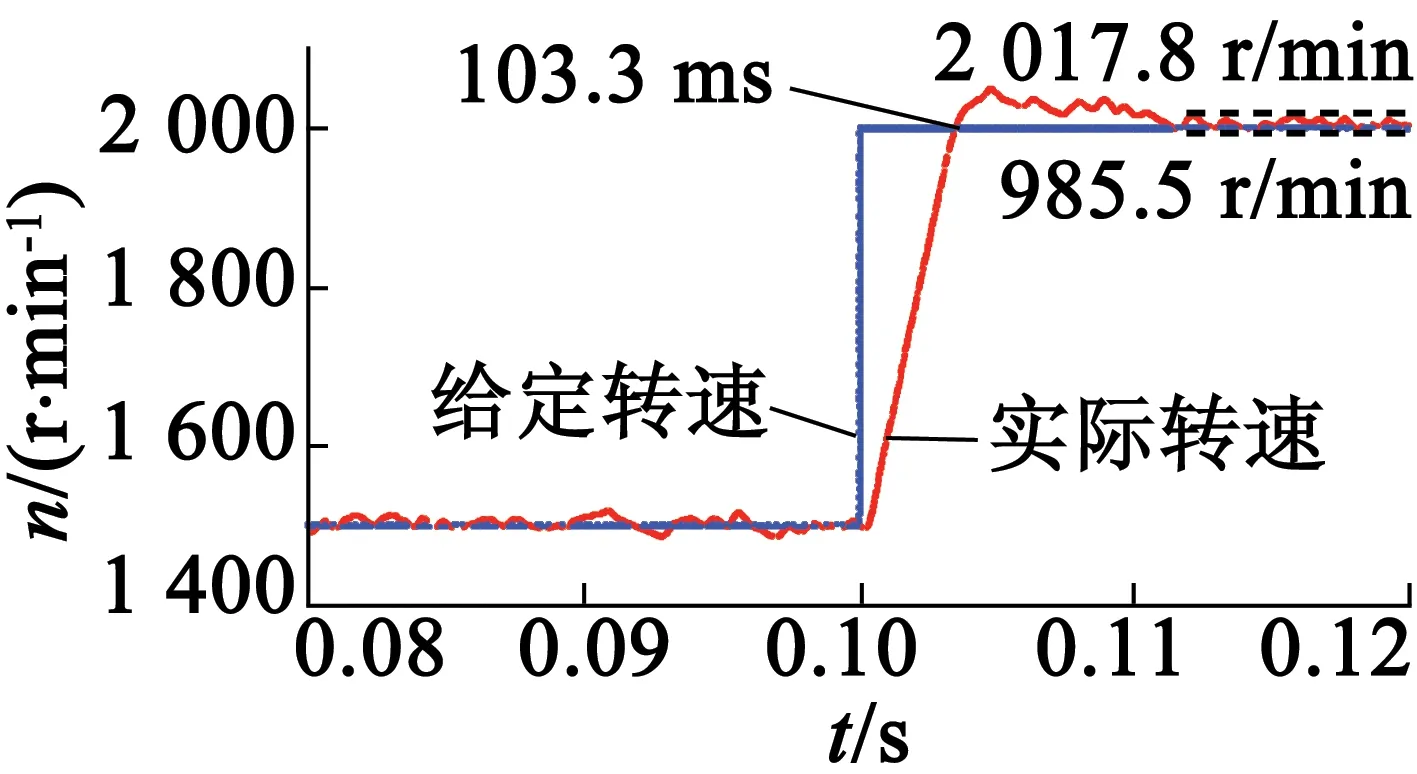
(b) 1 500 r/min～2 000 r/min

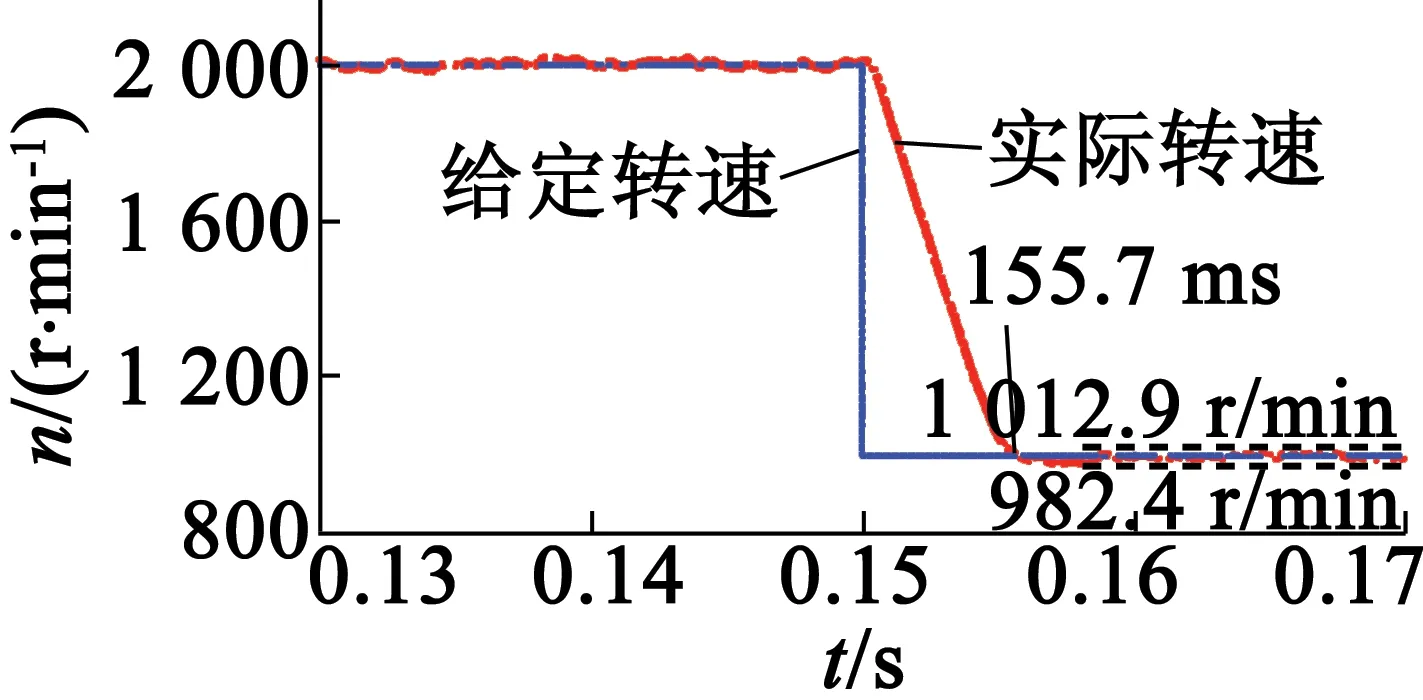
(c)2 000 r/min～1 000 r/min

由圖7和圖9的數據可以明顯看出，傳統的電機系統波形上升時間較大，穩態誤差較大；而加滑模后的波形上升時間縮短，穩態誤差較小。這說明了采用了二階滑模算法后的伺服系統，具有良好的速度跟蹤性能。

圖10(a)為當負載在0.05 s時由1 N·m變化為2 N·m時，采用傳統的速度計算方法時速度的響應。由圖10(a)可知，當負載變化時，采用傳統的差分算法的系統，電機恢復到穩態速度的時間為8.6 ms，超調量為5.3%。圖10(b)為當負載在0.05 s時由1 N·m變化為2 N·m時，采用二階滑模算法時速度的響應。由圖10(b)可知，當負載變化時，采用二階滑模算法的系統，電機恢復到穩態速度的時間為8 ms，超調量為3.9%。

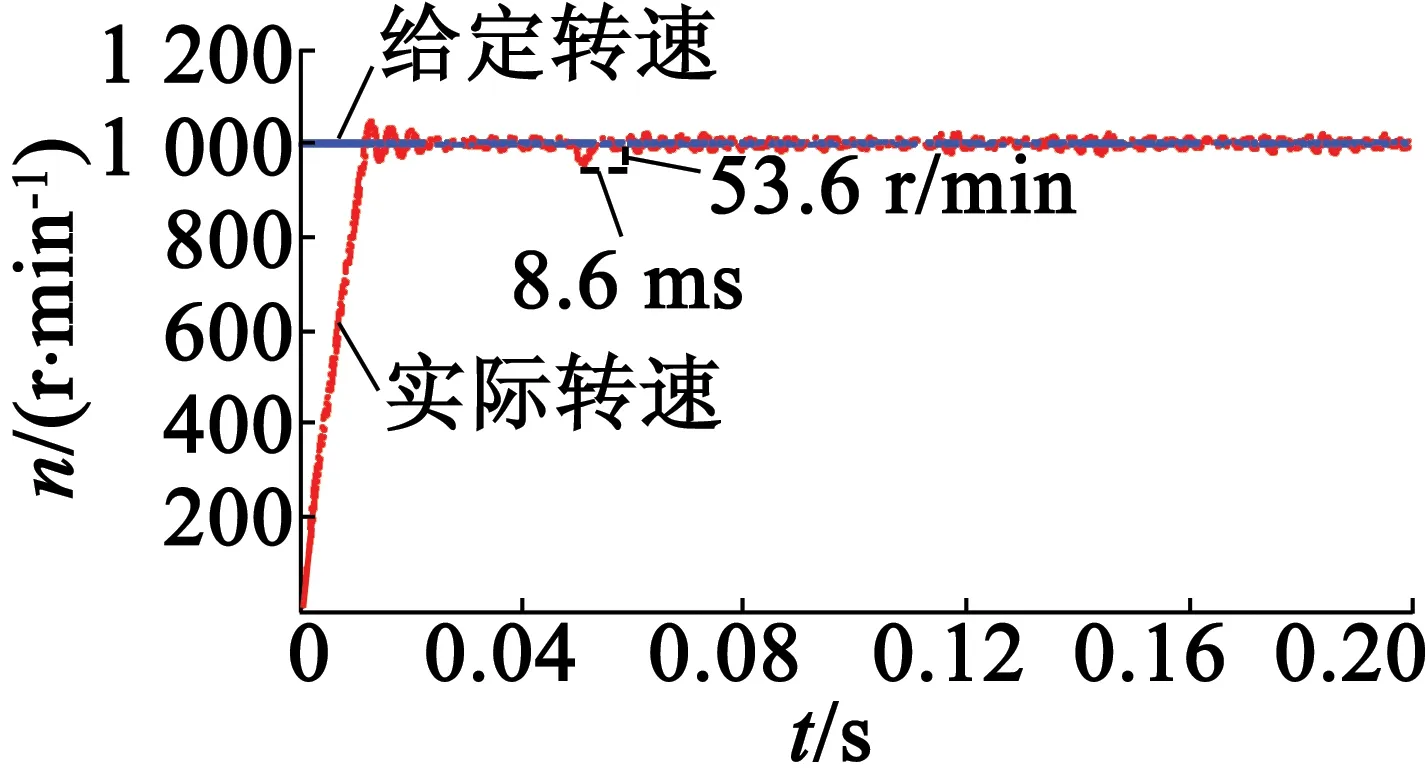
(a) 傳統的速度計算方法

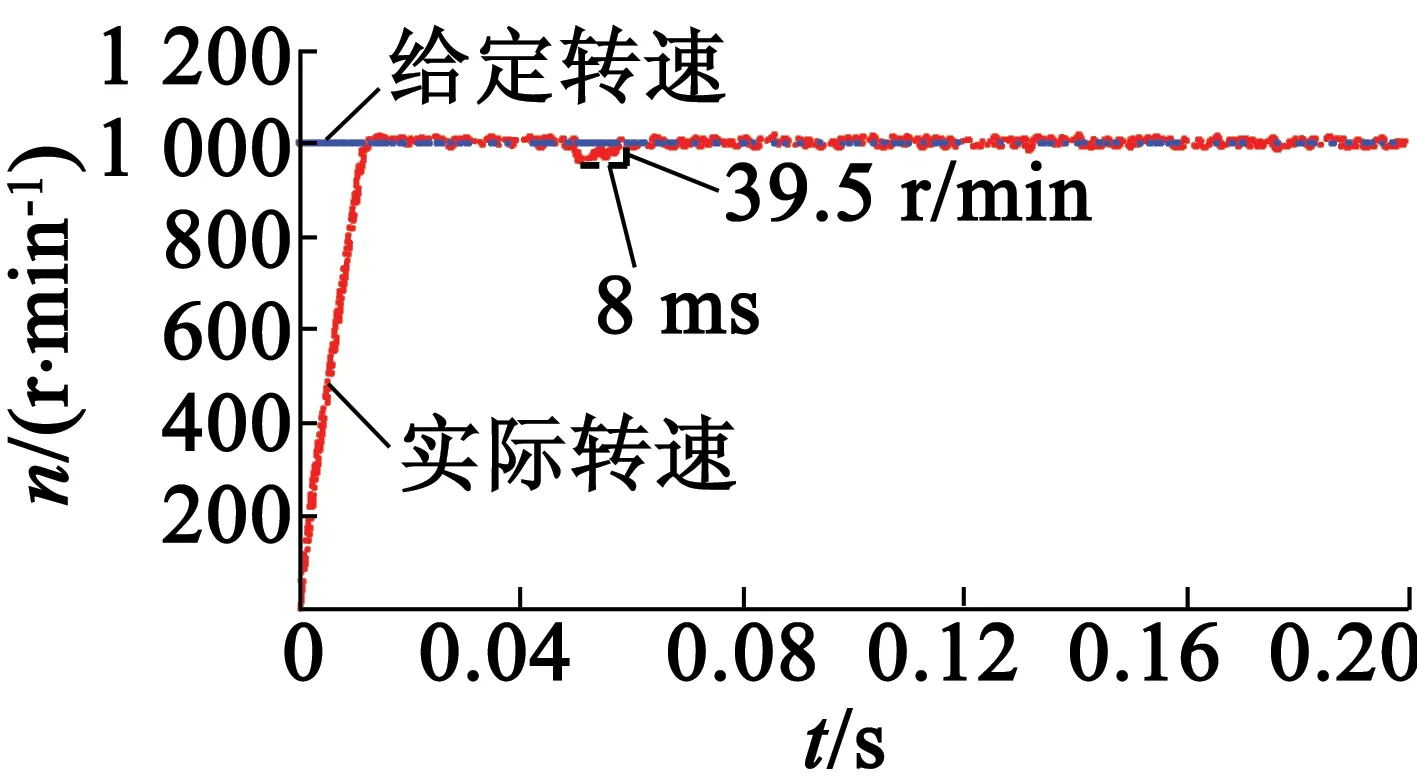
(b) 二階滑模算法

由圖10的數據還可以看出，負載轉矩變化時，傳統差分算法的系統抖動較明顯，超調量較大，長時間才能恢復系統的穩定；而采用二階滑模算法的系統，其速度的魯棒性和動態性能均有明顯提高。

4 結 語

本文介紹了一種二階滑模算法方法。根據二階滑模算法的原理，通過對實時位置信號進行采樣，經過二階滑模算法得到加速度，進而得到速度值，使速度反饋值能夠快速跟蹤負載的變化，從而能夠獲得良好的動態性能。仿真結果表明，該方案具有良好的動態性能，而且對電機參數依賴性小，具有較好的魯棒性和抗干擾性，有效地減少了系統運行過程中產生的抖動，提高了伺服系統的穩態性能。

[1] 張鹙娜,許翔軍,林曉梅.基于二階滑模的永磁同步電機直接轉矩控制[J].微電機,2010,43(10):33-35.

[2] 魯義寬.基于二階積分滑模的永磁同步電動機速度控制方法[J].微特電機,2015,43(9):66-69.

[3] 常雪劍,劉凌,崔榮鑫.永磁同步電機非奇異快速中斷可變邊界層滑模控制[J].西安交通大學學報,2015,49(6):53-59.

[4] 陳伯時,陳敏遜.交流調速系統[M].北京:機械工業出版社,2006.

[5] TRZYNADLOWSKI A M.異步電機的控制[M].李鶴軒譯.北京:機械工業出版社,2003.

[6] HAN Dong,LI Chun-Ru.Sliding-mode observers for systems with unknown inputs and measurement disturbances[J].Journal of Chongqing University (English Edition),2015,14(2):63-72.

[7] 唐廣雪, 朱學忠,張 磊.基于SMO的開關磁阻電機無位置傳感器控制仿真研究[J].機電工程,2016,33(3):303-307.

[8] BARTOLINI G,PISAN A,PUNTA E,etc.A survey of applications of second order sliding mode control to mechanical systems[J].International Journal of Control, 2005,76(9):875-892.

[9] 張曉光, 孫力, 陳小龍, 等.基于二階滑模觀測器的永磁同步電機無位置傳感器控制[J].電力自動化設備,2013,33(8):36-41.

[10] JI K H,SHEN J X,JIN M J.Low speed servo system with second-order sliding mode algorithm[C]//Proceeding of the 2012 IEEE International Symposium on Industrial Electronics,Hangzhou,P.R.China,2012(5):686-691.

[11] LEVANT A.Principles of 2-sliding mode design[J].Automatica,2007,43(4):576-586.

[12] BARTOLINI G，DAMIANO A.Robust speed and torque estimation in electrical drives by second-order sliding modes[J].IEEE Transactions on Control System，2003(11)：84-90.