基于獨(dú)立成分分析的復(fù)雜曲面加工誤差分離

張安社 陳岳坪 楊翊 唐清春

摘 要：研究基于獨(dú)立成分分析的復(fù)雜曲面加工誤差分離技術(shù)，旨在將復(fù)雜曲面加工誤差按照不同的誤差源進(jìn)行分離，克服當(dāng)前復(fù)雜曲面加工誤差分離時無法分離相近尺度誤差的問題.對各種誤差源所導(dǎo)致的加工誤差進(jìn)行建模，然后闡述獨(dú)立成分分析的原理和步驟；通過對混合后的信號進(jìn)行分離，判斷原始的4種信號與ICA分離出的4種信號之間相關(guān)性的大小，驗(yàn)證ICA用于解決分離混合信號問題的可行性；最后以實(shí)際加工中心加工的復(fù)雜曲面為例進(jìn)行實(shí)例驗(yàn)證，結(jié)果表明：應(yīng)用ICA可以有效地將復(fù)雜曲面相近尺度的加工誤差進(jìn)行分離，有利于進(jìn)一步對各誤差源進(jìn)行判定.

關(guān)鍵詞：獨(dú)立成分分析；主成分分析；加工誤差；復(fù)雜曲面

中圖分類號：TG506 DOI：10.16375/j.cnki.cn45-1395/t.2018.01.010

0 引言

當(dāng)今社會制造業(yè)發(fā)展速度越來越快，企業(yè)在數(shù)控加工精度方面提出了更高的要求.由于數(shù)控加工過程中各種誤差源的存在，導(dǎo)致加工精度不高的問題日益突出.通過分析判斷導(dǎo)致復(fù)雜曲面加工誤差產(chǎn)生的原因，然后針對造成誤差的不同誤差源進(jìn)行補(bǔ)償，以此來提高復(fù)雜曲面的加工精度.

目前加工誤差的分離辨識模型主要采用基于濾波的方法和統(tǒng)計的方法[1].Liao等[2]采用二維小波變換將汽缸蓋三維表面分解到不同尺度中進(jìn)行表達(dá)，使存在加工誤差的尺度顯示出來，用來檢測刀具崩裂、刀具與表面之間的相對顫振以及表面可能存在的泄露等.徐寧等[3]通過使用功率譜密度分析方案對復(fù)雜曲面表面形貌進(jìn)行分析.楊智等[4]利用小波分析理論對光學(xué)元件表面的加工誤差進(jìn)行分析.Huang[5]提出一種不依賴任何基函數(shù)就可以進(jìn)行分解的方法—經(jīng)驗(yàn)?zāi)B(tài)分解（EMD），該方法雖然可以根據(jù)信號的自身特征進(jìn)行分解，但是EMD在實(shí)際處理問題時會產(chǎn)生嚴(yán)重的模態(tài)混疊問題[6].

陳岳坪等[7-8]提出一種新的基于空間統(tǒng)計分析法的加工誤差分析方法：首先，通過三坐標(biāo)測量機(jī)檢測工件，獲取工件實(shí)際值與理論值的偏差；然后，根據(jù)空間統(tǒng)計分析原理對加工誤差數(shù)據(jù)進(jìn)行分析，最終把加工誤差中的系統(tǒng)誤差和隨機(jī)誤差分解出來.張磊等[9]通過分析傳統(tǒng)的誤差流模型只能解決線性模型的問題，提出加工誤差流的半?yún)?shù)回歸模型，對工序系統(tǒng)誤差和隨機(jī)誤差進(jìn)行分離.由以上可知空間統(tǒng)計分析原理只能將加工誤差分解為系統(tǒng)誤差和隨機(jī)誤差兩個部分，不能夠?qū)?dǎo)致加工誤差的各個誤差源進(jìn)行具體分析.針對上述問題，本文引入獨(dú)立成分分析（Independent Component Analysis，ICA）方法[10-11]，用該方法以復(fù)雜曲面加工誤差為研究對象，對測得的加工誤差進(jìn)行分離，分離出隱含在加工誤差中的各獨(dú)立成分，從而為進(jìn)一步對誤差源進(jìn)行分析與判定奠定了基礎(chǔ).

1 加工誤差的表示與建模

2 獨(dú)立成分分析與仿真

ICA起源于“雞尾酒聚會問題”（在有眾多人參加的雞尾酒舞會上，他們中的大多數(shù)人都在各自和自己的好友交談，并且交談的同時還夾雜有各種各樣的背景音樂，但是在酒會上的每個人都能夠準(zhǔn)確地聽到對方講話的詳細(xì)內(nèi)容），是一種從20世紀(jì)90年代開始流行起來用于解決多維混合獨(dú)立信號分離問題的新技術(shù).ICA以變量間互不相關(guān)為基本前提條件，然后對混合信號進(jìn)行分離，分析和判斷出隱含在混合信號中的各獨(dú)立信息成分.

2.1 獨(dú)立成分分析原理

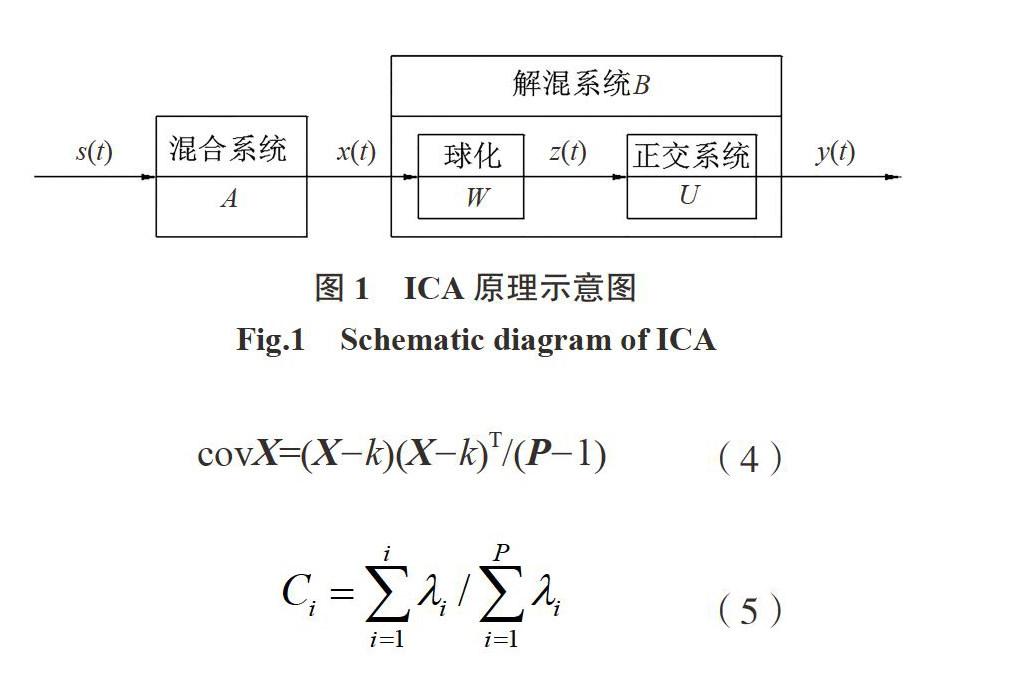
ICA基本原理是在獨(dú)立信號源s（t）經(jīng)過混合系統(tǒng)后生成x（t），x（t）經(jīng)過解混系統(tǒng)B進(jìn)行分離，使得輸出y（t）逼近s（t）.如圖1所示.

2.2 ICA算法的基本步驟

Step 1 對采集的信號X進(jìn)行中心化處理，使所采集信號的平均值為0.

Step 2 球化采集的原始信號，X→Z，精簡獨(dú)立分量計算過程.

Step 3 判斷獨(dú)立分量的個數(shù)m，處理后信號的協(xié)方差矩陣：

式中：P表示第i個信號源第P個信號的數(shù)值，可以看作是長度為P的向量；k為每一條的均值.

特征值的累計貢獻(xiàn)率：

式中：λi為covX的特征值.具有原始信號特征的強(qiáng)弱可由貢獻(xiàn)率的大小判斷，貢獻(xiàn)率越大它對應(yīng)的特征量具有源信號特征的能力越強(qiáng).根據(jù)貢獻(xiàn)率的大小確定m，初始化迭代次數(shù)p>1.

2.3 獨(dú)立成分分析仿真

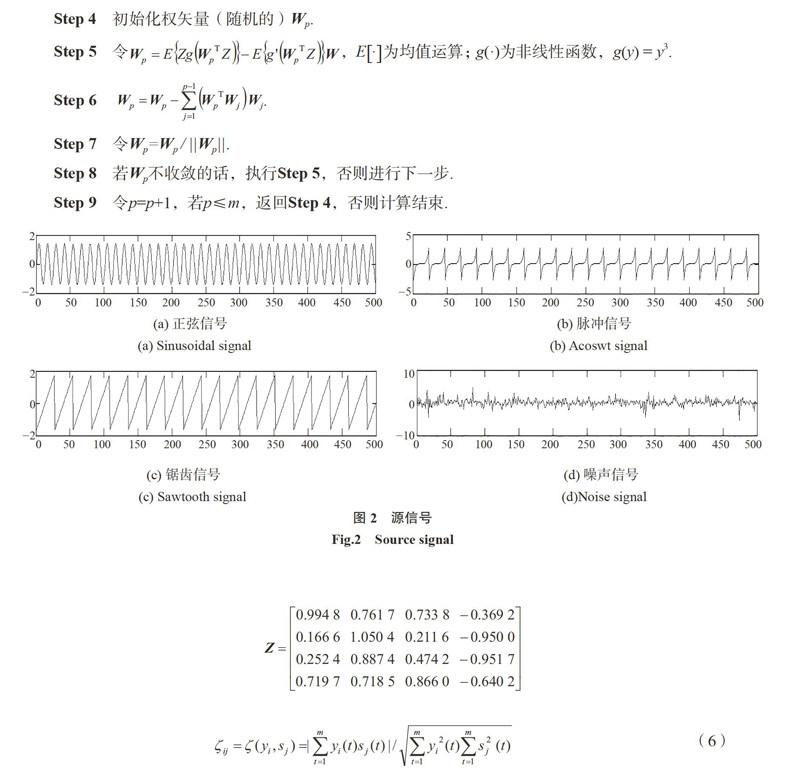
為驗(yàn)證ICA算法對混合信號的分離效果，分別以正弦信號、脈沖信號、鋸齒信號和噪聲信號4種互不相關(guān)的信號源進(jìn)行混合.4個信號源如圖2所示.

選取正態(tài)隨機(jī)分布的混合矩陣Z.

Z和圖2中的4個互不相關(guān)的信號生成的混合信號，如圖3所示.

應(yīng)用ICA對混合后的信號進(jìn)行分離，計算得到混合信號分離矩陣的估計，進(jìn)一步得到混合信號中獨(dú)立信號的估計，如圖4所示.

為驗(yàn)證ICA算法分離出各互不相關(guān)成分的精確度，使用相似系數(shù)對原始信號與ICA分離出信號的相似程度進(jìn)行評定.當(dāng)相似系數(shù)十分接近1，說明分離算法性能穩(wěn)定，所分離出的各獨(dú)立成分基本上保留源信號的全部信號特征.當(dāng)相似系數(shù)十分接近0，說明該種算法對混合信號不具備分離能力.

相似系數(shù)公式：

式中：yi是分離得到的信號，Sj是源信號，m是主成分個數(shù).

4種獨(dú)立信號之間的相似系數(shù)，如表1所示.

ICA分離出的信號與4種原始信號的相似系數(shù)，如表2所示.

由上表可以看出，分離出的信號與源信號相似系數(shù)絕對值接近1，說明ICA能夠很好地將混合信號分離，符合預(yù)期結(jié)果.

3 加工誤差分離實(shí)驗(yàn)

本實(shí)驗(yàn)曲面零件加工是在VMC650E立式銑床加工中心進(jìn)行，加工的數(shù)控NC代碼是由UG NX8.0自動生成.曲面加工采用粗加工、半精加工、精加工三道工序，粗加工采用的是Φ12 mm的端銑刀，半精加工和精加工采用的是Φ6 mm的球頭刀，使用德國海克斯康 Leitz Reference HP三坐標(biāo)測量機(jī)（Quindos7軟件，MPEE=0.9+ L/ 400 μm）為測量設(shè)備.配備接觸掃描式測頭，測頭直徑5 mm，在曲面上采集5條線，每條線1 000點(diǎn)，采樣方式如圖5、測量過程如圖6所示.

測得的5組數(shù)據(jù)如圖7所示.

獲得5組觀測數(shù)據(jù)后，下一步進(jìn)行誤差源數(shù)量估計即主成分分析.

對原始信號的5組數(shù)據(jù)分析，分別計算各信號的累積貢獻(xiàn)率Ci，確定出原始信號中主成分的數(shù)目，判斷誤差源的數(shù)目，結(jié)果如表3所示.

當(dāng)Ci大于 0. 95 時，即前i個主成分能夠包含原始誤差數(shù)據(jù) 95% 的信息，包含了i個不相關(guān)的主要誤差成分，根據(jù)上表可知，前2個主成分基本能完全解釋樣本的數(shù)據(jù)，即所測量的加工誤差中主要由2種誤差源構(gòu)成.

將測得的5組數(shù)據(jù)作為ICA的5組觀測信號，主成分個數(shù)為2，得到2組誤差成分的估計，如圖8所示.

利用傅里葉變換計算每個獨(dú)立分量的頻譜，如圖9、圖10所示.

由頻譜圖10可以看出不同頻率的波形緊湊、拖尾相對比較少，與周期性誤差特性相一致，推斷該復(fù)雜曲面在加工過程中存在周期性誤差.由頻譜圖9可以看出幅值突變的重現(xiàn)沒有規(guī)律可循，推斷該誤差主要是在切削過程中，由于刀具和加工表面的積屑瘤使表面形貌產(chǎn)生較大波動.通過找出造成加工誤差的來源，后續(xù)進(jìn)一步對誤差源進(jìn)行補(bǔ)償，為最終提高復(fù)雜曲面的加工精度奠定基礎(chǔ).

4 結(jié)論

1）闡述獨(dú)立成分分析原理和步驟，并對ICA算法進(jìn)行仿真，仿真結(jié)果表明ICA算法在獨(dú)立成分分析中具有較高的穩(wěn)定性.

2）采用ICA對實(shí)際復(fù)雜曲面的加工誤差進(jìn)行分離，取得很好的分離效果.驗(yàn)證該方法在復(fù)雜曲面加工誤差分離應(yīng)用中的有效性和可行性，為進(jìn)一步更加精確地對誤差的來源進(jìn)行判斷和補(bǔ)償?shù)於ɑA(chǔ).

參考文獻(xiàn)

[1]張發(fā)平，吳迪，張體廣，等.基于盲源信號分離的加工誤差分離方法研究[J].兵工學(xué)報，2016，37（9）： 1692-1699.

[2]LIAO Y ， STEPHENSON D A，NI J. Multiple-scale wavelet decomposition， 3D surface feature exaction and applications[J]. Journal of Manufacturing Science and Engineering， 2012， 134（1）： 011005.

[3]徐寧，侯仰海，邢彥峰.利用ACF和PSD對微觀表面特性研究[J].機(jī)械研究與應(yīng)用，2004，17（5）：54-56.

[4]楊智，戴一帆，王貴林.小波在基于功率譜密度特征曲線評價中的應(yīng)用[J]. 激光技術(shù)，2007，31（6）：627-629.

[5]HUANG N E. New method for nonlinear and nonstationary time series analysis： empirical mode decomposition and Hilbert spectral analysis [C]. Proc. of SPIE， 2000.

[6]HUANG N E， SHEN Z， LONG S R， et al. A new view of nonlinear waves： the Hilbert spectrum [J]. Annual Review of Fluid Mechanics， 1999， 31（1）： 417-457.

[7]陳岳坪，高健，鄧海祥，等. 復(fù)雜曲面零件在線檢測與誤差補(bǔ)償方法[J]. 機(jī)械工程學(xué)報，2012，48（23）：143-151.

[8]石光林， 陸維釗， 邵以東. 三坐標(biāo)測量機(jī)的計算機(jī)輔助測量系統(tǒng)研究[J]. 廣西工學(xué)院學(xué)報，2006， 17（3）：60-63.

[9]張磊，張志勝，周一帆，等. 基于半?yún)?shù)回歸模型的制造過程加工誤差流建模與分析[J]. 機(jī)械工程學(xué)報，2013，49（15）： 180-185.

[10]張賢達(dá)，保錚.盲信號分離[J]. 電子學(xué)報，2001，29（12A）： 1766-1771.

[11]李舜酩. 轉(zhuǎn)子振動故障信號的盲分離[J]. 航空動力學(xué)報，2005，20（5）：751-756.

Abstract：This study was based on the independent component analysis （ICA） of complex surfaces machining error separation technique. The aim was to separate the machining errors of a complex surface according to the different error sources， overcome the problem that the surface machining error separation cannot be separated from the similar scale error. Firstly， the machining errors caused by various error sources were modeled. Then the principles and steps of independent component analysis were described. Through the simulation of signal separation， the correlation size of simulation signals and ICA isolated signals was determined and then the feasibility of ICA was proved. Finally the actual complex surface was taken as an example for verification. The results showed that the complex surface machining errors of similar scale were effectively separated by ICA. It was helpful to determine the various error sources further.

Key words：independent component analysis （ICA）； principal component analysis； machining error； complex surface

（學(xué)科編輯：黎 婭）