基于概率協作表示的運動想象腦電分類算法

崔麗霞，楊濟民， 常洪麗

(山東師范大學物理與電子科學學院，山東 濟南 250358)

腦機接口(brain computer interface,BCI)是一種不依賴于正常的由外周神經和肌肉組成輸出通路的通訊系統[1],可以把大腦發出的信息直接轉換成驅動外部設備的控制命令，實現人與外界的直接交流以及對外部環境的控制。腦機接口技術的發展，為那些患有肌肉萎縮性側索硬化、腦干中風和脊髓損傷等疾病的人，提供了與外界交流的新方法。近幾十年來，腦機接口受到了多種學科研究人員的廣泛關注，在神經學、生物醫學工程和臨床康復等領域具有遠大的前景[2]。

特征提取是腦機接口系統中的關鍵技術之一，因為腦電信號具有隨機性和非平穩性，單一的分析方法并不能描述信號在時域和頻域的聯合分布信息。常用的時頻分析方法有短時傅里葉變換、小波變換以及S變換等[3]。傳統傅里葉變換對信號進行變換后，可以得到信號的頻域成分，但得不到信號不同頻率隨時間分布的信息，在實際應用中存在弊端。短時傅里葉變換是在傳統傅里葉變換的基礎之上加了一個窗函數，但由于窗函數固定，不能夠追蹤非平穩信號的動態性。1980年，法國地質物理學家Morlet首次提出小波的概念，繼承了短時傅里葉變換的局部化思想，而且窗口大小和形狀都可以改變，實現了多尺度分析[4]。1996年Stockwell等[5]提出了一種稱為S變換的新的信號處理技術，這是一種具備頻率獨立分辨率的時頻表示方法。S變換是短時傅里葉變換和小波變換的延伸和推廣，可以看作是一個具有可變窗函數的短時傅里葉變換，或者是一個連續小波的擴展[6-8]。S變換的優勢在于能夠提供多分辨率分析，同時保持每個頻率的絕對相位，使其非常適用于腦電信號的檢測[9]。

基于概率的協作表示方法是一種新的模式識別方法，已經在人臉識別領域成功應用[10]。在Wright等[11]提出的基于稀疏表示的分類方法(sparse representation based classification,SRC)中，以訓練樣本構造稀疏表示基，利用l1范數最小化作為約束，對測試樣本進行稀疏表示，通過比較不同類別的重構誤差來實現分類識別。雖然基于稀疏表示的方法具有良好的分類性能，但是Zhang等[12]指出，大多數研究過多強調了l1范數最小化在分類中的作用，真正起到關鍵性作用的是來自所有類別的訓練樣本對測試樣本的協作表示，而最小l1范數稀疏優化僅使得分類結果更加穩定。在協作表示的分類算法(collaborative representaion based classification,CRC)中，利用最小l2范數代替最小l1范數，使得運算復雜度大大減小。盡管SRC和CRC已經較好應用[13-14]，但是對于其分類機制仍然缺乏實質性的解釋，而ProCRC從概率的角度分析了CRC的分類機制，結合概率子空間的方法，提出了一種新的模式分類方法[10]。

目前，基于概率協作表示的方法只用于模式識別領域，鮮有用于腦電信號的分類識別中。本文中我們首先采用S變換對腦電信號進行濾波以及功率譜密度的特征提取，然后結合ProCRC進行識別分類，得到了較高的分類準確率，驗證了ProCRC算法在腦電信號處理中的有效性和適用性。

1 研究方法

1.1 S變換

S變換可以看成“相位正交”的連續小波變換，時域信號x(t)的小波變換定義為[5，15]：

(1)

其中，w(t,d)是母小波，尺度因子d可以控制小波w(t,d)的窗口寬度，從而控制分辨率。

那么，S變換與小波變換的關系可以表示為：

s(τ,f)=ei2πfτw(τ,d)，

(2)

其中，母小波函數定義為：

(3)

由此可見，S變換可定義為尺度可變的母小波和相位因子的乘積構成的連續小波變換。

另一方面，S變換的定義可以由短時傅里葉變換推導得到[16]：

(4)

其約束條件為：

(5)

窗口函數q(τ-t,f)是一個尺度可變的高斯函數，定義為：

(6)

S變換相對于短時傅里葉變換其優勢在于，標準偏差σ(f)是頻率分量f的函數：σ(f)=1/|f|。因此，窗口函數也是時間和頻率的函數，由于窗口的寬度是由頻率決定，所以很容易看到，在時間序列上，在較低頻率處窗口較寬，在較高頻率處窗口較窄，也就是說，這個窗口函數在低頻處提供較好的頻率分辨率，在高頻處提供較好的時間分辨率[17]。

本文主要利用S變換提取腦電信號的功率譜密度(power spectrum density,PSD)作為特征，來準確定位感知運動節律的頻譜變化。

1.2 基于概率協作表示的分類器

本文創新地將基于概率協作表示的分類算法應用于運動想象腦電信號的識別中，同時貝葉斯線性判別分析(bayesian linear discriminant analysis,BLDA)和梯度boosting(gradient boosting,GB)與兩種分類算法進行對比，驗證該算法的有效性。

1.2.1 概率協作表示

假設k類訓練樣本集合為x=[x1,x2,…,xk]，xk是類k的數據矩陣，并且其每一列為一個樣本向量。我們認為x是擴展類的數據矩陣，lx是x中所有候選類的標簽集,由sx表示x中所有樣本協同表示的線性子空間，在協作子空間sx中，每一個數據點h可以表示為：h=xα，其中α是表示向量。

由于x包含所有類的樣本，那么協作表示子空間sx比單獨每一個類xk的子空間要大的多。因此，盡管所有的xα都屬于sx，但是其被標記為lx的置信度是不同的，這取決于表示向量α的構成。

因此提出將sx作為一個概率協作子空間，不同的數據點對應于不同的概率：l(h)∈lx，l(h)是h的標簽。若用l2規范得到的α比較小，那么對應的p(l(h)∈lx)會比較大，反之亦然。我們使用高斯函數來定義這樣一個概率[10]：

(7)

這里c是一個常量，對應于公式(7)稱sx為概率協作子空間，sx內的數據點由α決定其所屬類別的概率。

1.2.2 概率子空間外的樣本表示

公式(7)定義了位于協作子空間sx內的數據點的概率表示，實際上測試樣本y通常位于sx之外。為了評估y屬于sx的概率p(l(y)∈lx),先試圖在sx內找到一個數據點h，然后計算以下兩個概率：p(l(h)∈lx)以及y和h具有相同類標簽的概率p(l(h)=l(y))，可以得到：

p(l(y)∈lx)=p(l(y)=l(h)|l(h)∈lx)·p(l(h)∈lx)，

(8)

由公式(7)可以求得p(l(h)∈lx)，而p(l(y)=l(h)|l(h)∈lx)可以通過h和y之間的相似度來測量，這里采用高斯內核去定義[10]：

(9)

這里κ是常量，高斯核是廣泛使用的一種衡量圖形中兩個頂點相鄰相似度的方法，其優點在許多應用中凸顯出來，比如數據簡化，人臉面部分析，圖像聚類等。

由公式(7)～(9)，可以推出：

(10)

為了最大化概率p(l(y)∈lx)，我們將對數運算應用于公式(10)，可以得到[10]：

(11)

這里μ=c/κ,以上公式給出了位于sx之外的測試樣本y的概率表示。值得注意的是，公式(11)的表達與協作表示的分類是一致的[12]，但是此公式有著明確的概率解釋。

1.2.3 特定類子空間的概率

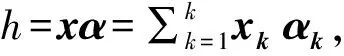
(12)

其中δ是常量，lx為類標簽。對于sx空間外的一個查詢樣本y,可得到l(y)=k的概率：

p(l(y)=k) =p(l(y)=l(h)|l(h)=k)·p(l(h)=k)

=p(l(y)=l(h)|l(h)=k)·p(l(h)=k|l(h)∈lx)·p(l(h)∈lx)，

(13)

只要k∈lx，公式(9)的概率與k無關，可得到p(l(y)=l(h)|l(h)=k)=p(l(y)=l(h)|l(h)∈lx)，由公式(11)～(13)可得[10]：

p(l(y)=k) =p(l(y)∈lx)·p(l(h)=k|l(h)∈lx)

(14)

其中γ=δ/κ。

1.2.4ProCRC模型

我們需要在sx空間內找到一個公共點，然后最大化聯合概率p(l(y)=1,…,k)，就可以檢測到最高概率的p(l(y)=k)，來確定y的類標簽。假設事件l(y)=k互相獨立，則有：

maxp(l(y)=1,…,k) =max∏kp(l(y)=k)

(15)

運用對數運算，并忽略常數項，可以得到[10]：

(16)

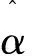
(17)

(18)

其分類規則為：

(19)

以上所述的分類器即為基于概率協作表示的分類器[10](ProCRC)。

分類任務的魯棒性可以通過使用l1范數來評價損失函數，以上提出的概率協作表示模型中，對公式(9)使用拉普拉斯內核代替高斯內核：

p(l(y)=l(h)|l(h)∈lx)∝exp(-κ‖y-h‖1)，

(20)

與ProCRC推導相似，我們可以得到具有魯棒性的ProCRC(Robust ProCRC,R-ProCRC)模型[10]：

(21)

其分類規則與等式(19)一致。

(22)

注意：I是單位矩陣，那么可以通過T得到α：

(23)

盡管R-ProCRC模型是凸的，但是沒有封閉解，采用IRLS來求解α。首先引入對角加權矩陣wx：

wx(i,i)=1/|x(i,:)α-yi|，

(24)

這里的x(i,:)代表矩陣x的第i行，給定wx，等式(21)可以重新計算為：

(25)

系數向量α更新為[10]：

(26)

交替地更新加權矩陣wx和系數向量α，直到收斂或者達到迭代次數后停止。

2 實驗設計

2.1 數據庫

本文所提出的算法采用BCI競賽數據庫Ⅲ中的數據集Ⅰ來驗證算法的有效性[18]。該腦皮層電圖(electrocorticography，ECoG)數據采自于一個病灶性癲癇患者，在被試者的右半球大腦運動皮層表面放置了一個88的網格狀鉑電極，尺寸大小為8 cm8 cm,包含64個信道。在被試者的大腦中植入的電極要保持一到兩周的時間，而且ECoG數據的記錄是在一周內的不同的兩天完成。在整個實驗過程中，被試者坐在舒適的座位上，面對電腦屏幕，并根據實驗要求重復想象伸舌頭和左小指動這兩個動作[19]。每次實驗開始時，屏幕中央會出現運動想象任務的圖片，為了避免視覺激發電位，數據記錄將在提示的0.5 s之后進行。如圖1所示，為一次實驗的進程[20]。

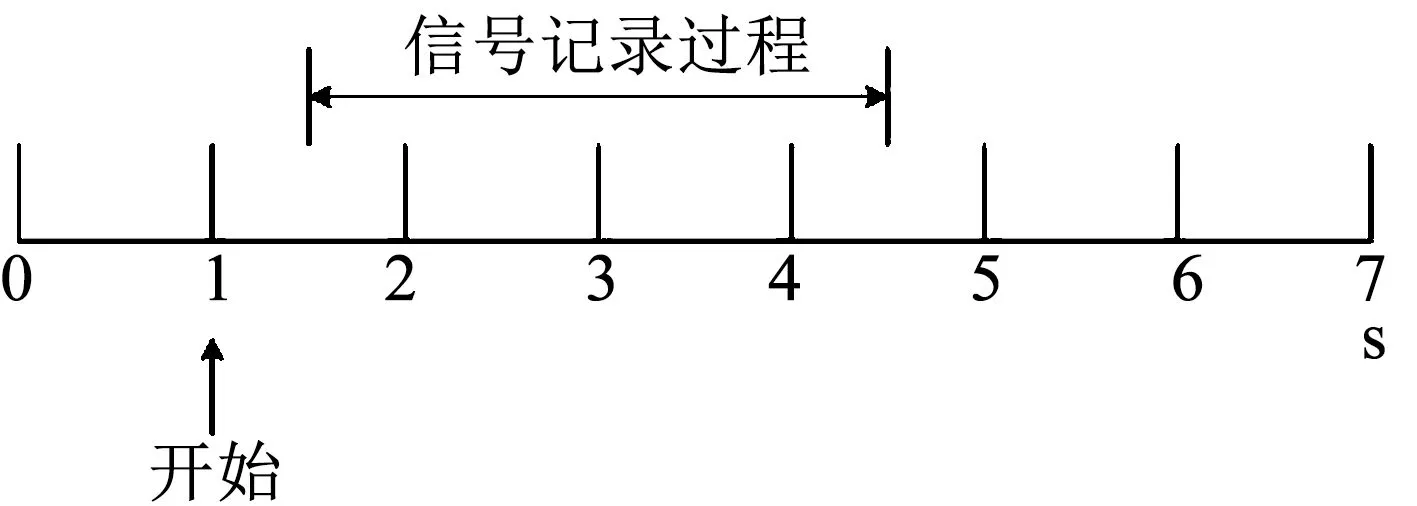
圖1 一次實驗的記錄過程Fig.1 The recording process of one trial

該數據集的采樣頻率為1 000 Hz,并包含一個訓練集和一個測試集，數據存儲格式為“實驗次數信道數樣本數”，訓練集包括278次實驗，測試集包括100次實驗，由于實驗包含兩類運動想象任務，訓練集中每一類想象任務的實驗次數為139次。

2.2 實驗流程

本文提出了基于S變換的特征提取和基于概率協作表示的分類器相結合的腦電信號識別的算法，該算法主要包括預處理，特征提取和分類識別等3個部分，基本流程如圖2所示。

實驗中所用數據庫中的腦電信號采樣頻率較高,為了減少數據存儲和提高算法效率，首先對ECoG信號進行1 000 Hz到100 Hz的降采樣處理。

其次，采用S變換對數據進行濾波和特征提取，頻帶范圍設置為1 ～ 35 Hz，間隔為1 Hz，這樣一方面保留了運動想象腦電信號的主要波段，另一方面起到了濾波作用。然后，計算得到基于S變換的PSD特征，得到的特征矩陣結構為：實驗次數64信道PSD特征數目，一次實驗當中的特征數為N=CM，C是信道數目，M代表一個信道中的PSD特征數目。

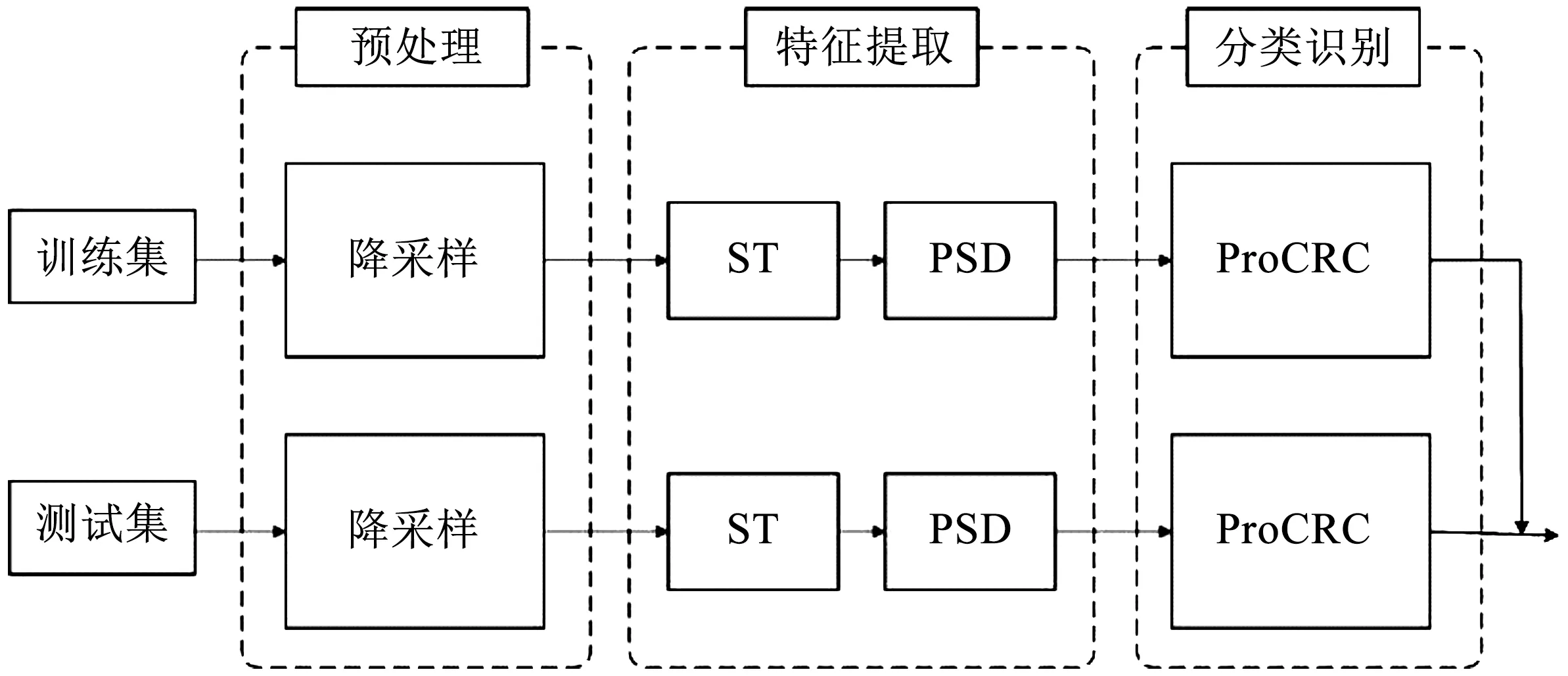
圖2 算法框圖Fig.2 Block diagram of the algorithm

最后，將提取好的特征矩陣送到ProCRC分類器，實驗結果輸出0和1，分別代表兩種運動想象任務。基于ProCRC算法過程如下：

(1)對訓練特征集進行標準化處理，使得特征集的每一列具有單位l2范數；

(2)設置參數γ，μ；

(3)計算投影矩陣

(4)將測試樣本投影到T上，獲得編碼系數α；

(5)引入對角加權矩陣，利用IRLS交替更新系數向量，直到達到設置的迭代次數(與測試樣本數目相同)；

(6)計算概率

(7)輸出所屬類別

3 結果分析

BCI系統的評估標準有很多，最常用的評估標準是分類準確率,定義如下：

本文所有的算法程序均在MATLAB環境下運行。在ProCRC中，有兩個可調節參數來控制分類的性能，分別為γ和μ。最優的γ和μ值可以提供更好的分類準確率，圖3描述了在不同參數γ和μ值下分類準確率的變化。從縱向上來看，對應于不同的γ和μ值，該算法的分類準確率表現出明顯的差異性。從橫向上來看，當參數μ的值為1時，該算法的分類性能比較穩定，最高可以達到90%，表現出了優異的分類性能。

圖3 在不同參數γ和μ值下所表現的分類性能對比Fig.3 Comparison of the classification performance under different parameters of γ and μ

良好的特征提取與分類器的最佳匹配能夠提高整個算法的性能，為了說明ProCRC具有優異的分類性能，將其與BLDA以及GB分類器進行對比。表1總結了基于ST的PSD特征和不同的分類器相結合得到的分類準確率。Fisher線性判別分析(fisher linear discriminant analysis,FLDA)是為了得到一個最佳判別向量，這個向量使得類間離散度和類內離散度之比最大化，以完成二類或多類的分類問題。BLDA可以看成是FLDA的一個擴展，是基于概率回歸網絡構成的[21]。GB是一種集成學習算法，可以將多個弱分類器組合成一個強分類器，從而達到提升分類器性能的目的。GB算法在損失函數的梯度下降方向上建立新的弱分類模型，使損失函數越來越小，不斷改善分類性能，是一種迭代優化算法[22]。

為了保證比較的公平性，與ProCRC相比較的這兩種分類器都是線性分類器。實驗結果表明，本文所提出的方法能夠得到最好的分類結果，驗證了基于概率協作表示的分類算法在腦電信號的分類識別中的有效性。

表1 不同分類器的分類準確率Table 1 Classification accuracy of different classifiers

4 結語

本文針對腦電信號的分類識別，提出了一種基于概率協作表示的分類器(ProCRC)，具有明確的概率解釋。該算法采用了概率協作表示框架，最大化表征測試樣本屬于每個類別的概率，有效地利用了所有類別的訓練樣本來推斷測試樣本的標簽類別，具有高效性。

在實驗過程中，我們利用BCI競賽數據庫Ⅲ中的數據集Ⅰ來驗證所提出算法的有效性。首先對運動想象信號進行了預處理和特征提取，然后將有效的特征和分類器結合，通過與兩種典型的BLDA和GB分類器對比，本文提出的ProCRC通過調節參數，可以保持穩定的分類性能，分類準確率能夠達到90%，驗證了該算法在腦電信號分類識別中的有效性。

腦電信號的識別分類，是腦機接口系統關鍵技術的研究熱點，本文所提出的基于概率的協作表示分類器準確率高，性能穩定，在處理大數據的腦電信號時具有較大的可拓展性，對于研究ProCRC在腦電信號識別領域中的應用具有一定的借鑒意義。

參考文獻：

[1]WOLPAW J R,BIRBANME R N,McFARLAND D J,et al.Brain-computer Interface for communication and control[J].Clinical Neurophysiology,2002,113(6):767-791.

[2]GAO S K,WANG Y J,GAO X R,et al.Visual and auditory brain-computer interfaces[J].IEEE Transactions on Biomedical Engineering,2014,61(5):1436-1447.

[3]XU F,ZHOU W,ZHEN Y,et al.Classification of ECoG with modified S-transform for brain computer interface[J].Journal of Computational Information Systems,2014,10(18):8029-8041.

[4]潘泉,張磊,孟晉麗,等.小波濾波方法及應用[M].北京:清華大學出版社,2006.

[5]STOCKWELL R G,MANSINHA L,LOWE R P,Localization of the complex spectrum：the S transform[J].IEEE Transaction on Signal Processing,1996,44(4):998-1001.

[6]YAN Y,ZHU H.The generalization of discrete Stockwell transforms[M]//19th European Signal Processing Conference.[S.l.]：IEEE,2011:1209-1213.

[7]STOCKWELL R G.Abasis for efficient representation of the S-transform[J].Digital Signal Processing,2007,17(1):371-393.

[8]UYAR M,YILDIRIM S,GENCOGLU M T,An expert system based on S-transform and neural network for automatic classification of power quality disturbances[J].Expert Systems with Applications,2009,36(3):5962-5975.

[9]PINNEGAR C R,MANSINHA L.The s-transform with windows of arbitrary and varying shape[J].Geophysics,2003,68(10):381-385.

[10]CAIS J,ZHANG L,ZUO W M,et al.A probabilistic collaborative representation based approach for pattern classification[M]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR).[S.l.]: IEEE,2016:2950-2959.

[11]WRIGHT J,YANG A Y,GANESH A,et al.Robust face recognition via sparse representation[J].IEEE transactions on pattern analysis and machine intelligence,2009,31(2):210-227.

[12]ZHANG L,YANG M,FENG X C.Sparse representation or collaborative representation: Which helps face recognition? [M]//2011 IEEE International Conference on Computer Vision.[S.l.]: IEEE,2011:471-478.

[13]SHIN Y,LEE S,AHN M,et al.Noise robustness analysis of sparse representation based classification method for non-stationary EEG signal classification[J].Biomedical Signal Processing and Control,2015,21:8-18.

[14]MIAO M,WANG A,LIU F.A spatial-frequency-temporal optimized feature sparse representation-based classification method for motor imagery EEG pattern recognition[J].Medical & Biological Engineering & Computing,2017,55(9):1589-1603.

[15]McFADDEN P D,COOK J G,FORSTER L M.Decomposition of gear vibration signals by the generalized S-transform[J].Mechanical Systems and Signal Processing,1999,13(5):691-707.

[16]GHAFFARZADEH H.A classification method for pulse-like ground motions based on S-transform[J].Natural Hazards,2016,84(1):1-16.

[18]BLANKERTZ B.BCI Competition III[EB/OL].[2017-10-11].http://www.bbci.de/competition/iii/#data_set_i.

[19]LAL T N,HINTERBERGER T,WIDMAN G,et al.Methods towards invasive human brain computer interfaces[J].Advances in neural information processing systems,2005,17: 737-744.

[20]XU F,ZHOU W,ZHEN Y,et al.Classification of motor imagery tasks for electrocorticogram based brain-computer interface[J].Biomedical Engineering Letters,2014,4(2):149-157.

[21]HOFFMANN U,VESIN J M,EBRAHIMI T,et al.An efficient P300-based brain-computer interface for disabled subjects[J].Journal of Neuroscience Methods,2008,167(1):115-125.

[22]ZHANG Y,ZHOU W,YUAN S,et al.Seizure detection method based on fractal dimension and gradient boosting[J].EpilepsyBehavior,2015,43:30-38.