高考推理與證明高分突破

■安徽省阜陽市太和中學 岳 峻

“推理與證明”是數學的基本思維過程,也是人們學習和生活中經常使用的思維方式。推理一般包括合情推理和演繹推理,推理與證明貫穿于高中數學的整個體系,它是新課標教材的一個亮點,是對以前所學知識與方法的總結、歸納,并對同學們的后繼學習起到引領的作用。

考點突破一、合情推理

考綱要求：了解合情推理的含義,能進行簡單的歸納推理和類比推理,體會并認識合情推理在數學發(fā)現中的作用。

權威解讀：歸納推理是由某類事物的部分對象具有某些特征,推出該類事物的全部對象都具有這些特征的推理,或者由個別事實概括出一般結論的推理,稱為歸納推理(簡稱歸納)。簡而言之,歸納推理是由部分到整體,由個別到一般的推理;類比推理是由兩類對象具有某些類似特征和其中一類對象的某些已知特征,推出另一類對象也具有這些特征的推理,稱為類比推理(簡稱類比)。歸納推理和類比推理統(tǒng)稱為合情推理。

例1 (2016年山東卷)觀察下列等式:

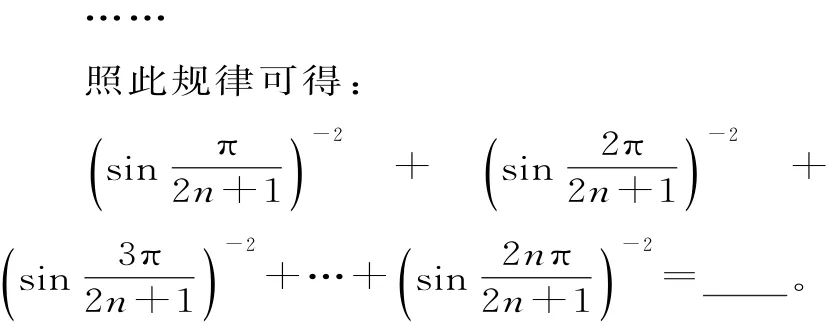
解析：觀察易知3=1+2,5=2+3,7=3+4,9=4+5,…,歸納可得2n+1=n+(n+1)。

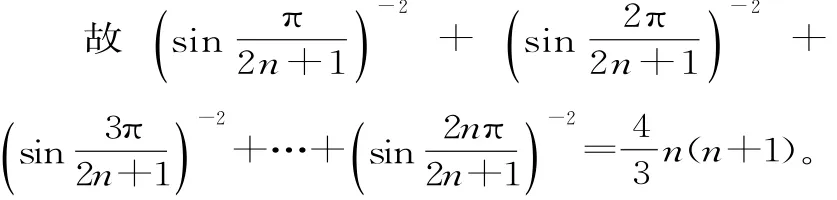
點評:在解決問題的過程中,合情推理具有猜測和發(fā)現結論、探索和提供思路的作用,有利于培養(yǎng)同學們的創(chuàng)新意識。

跟蹤訓練1：(2018屆安徽太和中學質量檢測)觀察以下各等式:

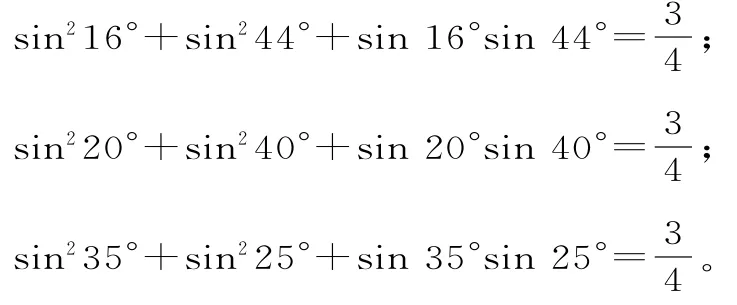
(1)分析上述各式的共同特點,猜想出一般規(guī)律的等式;

(2)并借助于正弦定理、余弦定理對等式的正確性給出證明。

提示：(1)設α+β=60°,則sin2α+sin2β+sinαsin

(2)設a,b,c是△ABC的三個內角A,B,C的對應邊,若A+B=60°,則:

c2=a2+b2-2abcosC=a2+b2+ab。

又a=2RsinA,b=2RsinB,c=2RsinC,代入上式并化簡得:

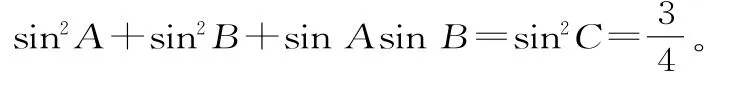
例2 如圖1,P是斜三棱柱ABC-A1B1C1的側棱BB1上的一點,PM⊥BB1且交AA1于M,PN⊥BB1且交CC1于N。

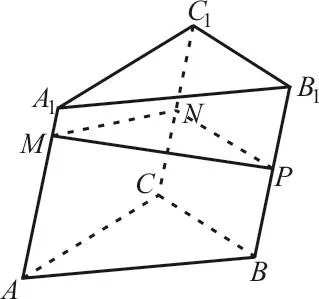
圖1

(1)證明:CC1⊥MN;

(2)類比平面幾何的余弦定理,寫出斜三棱柱ABC-A1B1C1的三個側面面積與其中兩個側面所成的二面角之間的關系式,并加以證明。

解析：(1)因為PM⊥BB1,PN⊥BB1,并且PN,PM?平面MNP,PM∩PN=P,所以BB1⊥平面MNP。

因為MN?平面MNP,所以BB1⊥MN。

又因為BB1∥CC1,所以CC1⊥MN。

(2)由題意可知,兩個側面所成的二面角M-BB1-N的平面角為∠MPN。

在△MPN中,MN2=MP2+NP2-2MP·NPcos∠MPN。

兩邊同乘BB21,化簡可得:

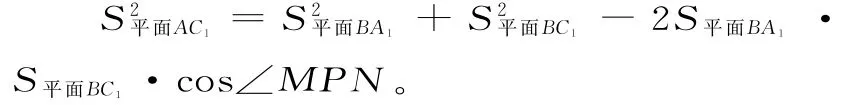
點評:高考中的類比一般包括由數到數的類比、由形到形的類比、論證方法的類比,通過兩類事物的類比可以對事物的性質有更深刻的理解。

跟蹤訓練2：(2018年湖南株洲六校聯考)對于問題:“已知關于x的不等式ax2+bx+c＞0的解集為(-1,2),求關于x的不等式ax2-bx+c＞0的解集。”

給出如下一種解法:

由ax2+bx+c＞0的解集為(-1,2),得a(-x)2+b(-x)+c＞0的解集為(-2,1),即關于x的不等式ax2-bx+c＞0的解集為(-2,1)。

故所求不等式的解集為(-3,-1)∪(1,2)。

考點突破二、邏輯推理

考綱要求：了解演繹推理的含義,了解合情推理和演繹推理的聯系和差異;掌握演繹推理的“三段論”,能運用“三段論”進行一些簡單的演繹推理。

權威解讀：演繹推理是根據已有的事實和正確的結論(包括定義、公理、定理等),按照嚴格的邏輯法則得到新結論的推理過程。培養(yǎng)和提高學生的演繹推理或邏輯證明的能力是高中數學課程的重要目標。

例3 (2016年新課標Ⅱ卷)有三張卡片,分別寫有1和2,1和3,2和3。甲,乙,丙三人各取走一張卡片,甲看了乙的卡片后說:“我與乙的卡片上相同的數字不是2。”乙看了丙的卡片后說:“我與丙的卡片上相同的數字不是1。”丙說:“我的卡片上的數字之和不是5。”則甲的卡片上的數字是____。

解析：第一句意味著甲與乙的卡片上相同的數字不是2,等價于丙的卡片不是(1,3),第三句意味著丙的卡片上的數字之和不是5,等價于丙拿的不是(2,3),所以丙拿的是(1,2);第二句意味著乙與丙的卡片上相同的數字不是1,等價于甲的卡片不是(2,3),所以乙的卡片是(2,3),甲的卡片只能是(1,3)。

點評:本題以三個人,三張不同卡片,每人持有一張作為問題的背景,依據三人的陳述,確定三個人各自持有的卡片。本題要求同學們理解所陳述的含義,根據陳述排除不合要求的分配情況,最終確定每個人手中的卡片內容。試題注重考查同學們邏輯思維的基本素養(yǎng),沒有現成的解題套路,但有利于考查同學們獨立思考、解決問題的能力。

跟蹤訓練3:(2017年新課標Ⅱ卷)甲、乙、丙、丁四位同學一起去向老師詢問成語競賽的成績。老師說:你們四人中有2位優(yōu)秀,2位良好,我現在給甲看乙、丙的成績,給乙看丙的成績,給丁看甲的成績。看后甲對大家說:我還是不知道我的成績。根據以上信息,判斷( )。

A.乙可以知道四人的成績

B.丁可以知道四人的成績

C.乙、丁可以知道對方的成績

D.乙、丁可以知道自己的成績

提示：由甲的說法可知乙、丙一人優(yōu)秀一人良好,則甲、丁一人優(yōu)秀一人良好;乙看到丙的結果則知道自己的結果,丁看到甲的結果則知道自己的結果,故選D。

例4 (2016年北京卷)袋中裝有偶數個球,其中紅球、黑球各占一半。甲、乙、丙是三個空盒。每次從袋中任意取出兩個球,將其中一個球放入甲盒,如果這個球是紅球,就將另一個球放入乙盒,否則就放入丙盒。重復上述過程,直到袋中所有球都被放入盒中,則( )。

A.乙盒中黑球不多于丙盒中黑球

B.乙盒中紅球與丙盒中黑球一樣多

C.乙盒中紅球不多于丙盒中紅球

D.乙盒中黑球與丙盒中紅球一樣多

解析：每次從袋中抓出兩個球的情形有四種:①紅黑;②紅紅;③黑黑;④黑紅。

情形①放入甲盒的是紅球,導致乙盒中黑球加1;情形②放入甲盒的是紅球,導致乙盒中紅球加1;情形③放入甲盒的是黑球,導致丙盒中黑球加1;情形④放入甲盒的是黑球,導致丙盒中紅球加1。

不妨設①有a次,②有b次,③有c次,④有d次,則甲盒有紅球a+b個,黑球c+d個;乙盒有黑球a個,紅球b個;丙盒有黑球c個,紅球d個。由于紅球、黑球數目相等,所以a+2b+d=a+2c+d,即b=c,故乙盒中紅球與丙盒中黑球一樣多,所以選B。

點評:上面對球的取放規(guī)則進行分析和邏輯推理,環(huán)環(huán)相扣,準確地把握取放規(guī)則的內涵,其突破口是將抽象的取放法則數據化,發(fā)現內在規(guī)律,進而解決問題。

跟蹤訓練4:(2017年北京卷)某學習小組由學生和教師組成,人員構成同時滿足以下三個條件:

(i)男學生人數多于女學生人數;

(ii)女學生人數多于教師人數;

(iii)教師人數的兩倍多于男學生人數。

①若教師人數為4,則女學生人數的最大值為____;

②該小組人數的最小值為____。

①當z=4時,8＞x＞y＞4,所以x的最大值為7,y的最大值為6,故女學生人數的最大值為6。

考點突破三、反證法

考綱要求：了解反證法的思考過程和特點。

權威解讀：反證法是間接證明法的一類,是從反方向證明的證明方法,即:肯定題設條件而否定結論,經過推理導出矛盾,從而證明原命題。反證法的邏輯原理是逆否命題和原命題的真假性相同。

(1)求橢圓C的標準方程;

(2)過點F1的直線l1與橢圓C交于M,N兩點,過點F2的直線l2與橢圓C交于P,Q兩點,且l1∥l2,證明:四邊形MNPQ不可能是菱形。

又c2=a2-b2,所以橢圓C的標準方程

圖2

(2)由(1)可知F1(-1,0),如圖2,易知直線MN不能平行于x軸,所以令直線MN的方程為x=my-1,M(x1,y1),N(x2,y2)。

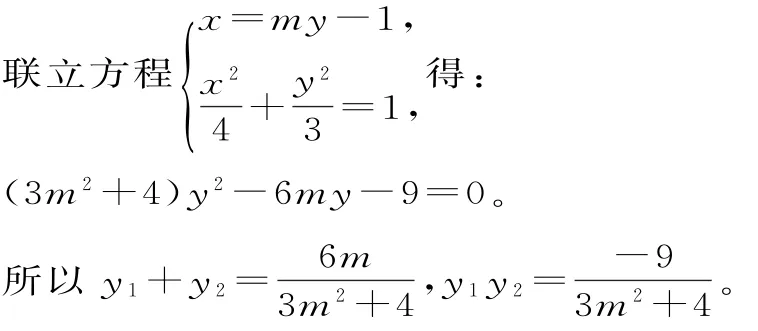
此時|MN|=(1+m2)[(y1+y2)2-4y1y2]。

同理,令直線PQ的方程為x=my+1,P(x3,y3),Q(x4,y4)。

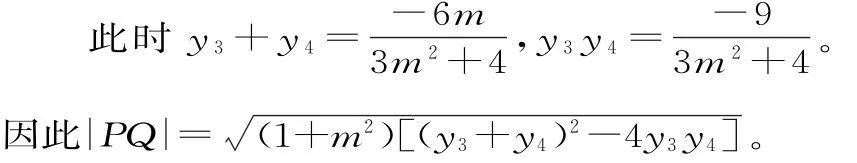
故|MN|=|PQ|,所以四邊形MNPQ是平行四邊形。

又x1x2=(my1-1)(my2-1)=m2y1y2-m(y1+y2)+1,所以有(m2+1)y1y2-m(y1+y2)+1=0,整理得到即12m2+5=0。

上述關于m的方程顯然沒有實數解,故四邊形MNPQ不可能是菱形。

點評:反證法適宜證明“存在性問題,唯一性問題”,帶有“至少有一個”或“至多有一個”等字樣的問題,直接證明有困難時,常采用反證法。

跟蹤訓練5:(2017年德州一模)如果△A1B1C1的三個內角的余弦值分別等于△A2B2C2的三個內角的正弦值,則△A2B2C2是____三角形。(填“銳角”、“直角”或“鈍角”)

提示：由條件知,△A1B1C1的三個內角的余弦值均大于0,則△A1B1C1是銳角三角形。

假設△A2B2C2是銳角三角形,則:

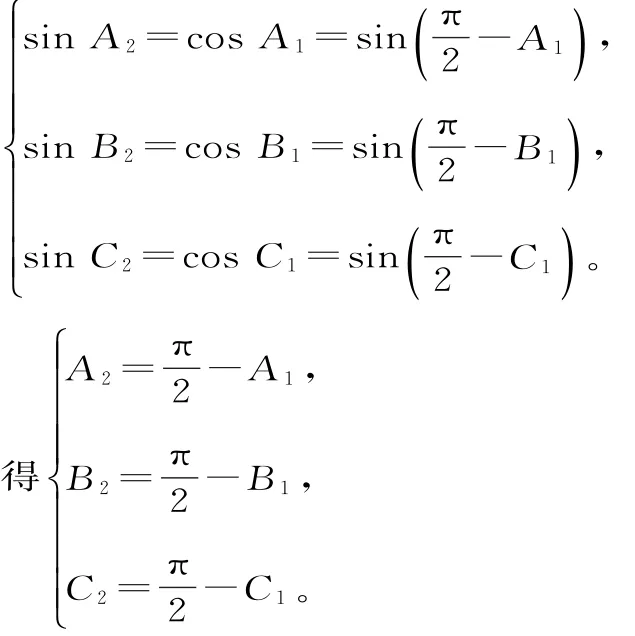
那么A2+B2+C2=,這與A+B+C=π相矛盾,所以假222設不成立。

又顯然△A2B2C2不是直角三角形,故△A2B2C2是鈍角三角形。

跟蹤訓練6:(2018屆阜陽第一次質量檢測)已知f(x)=ax2+bx+c,若a+c=0,f(x)在[-1,1]上的最大值為2,最小值為

提示：(1)假設a=0,f(x)=bx,顯然b≠0,f(x)在[-1,1]上是單調函數,則f(x)的最大值為|b|,最小值為-|b|,此時|b|+(-|b|)=0,與已知條件相矛盾,所以a≠0。

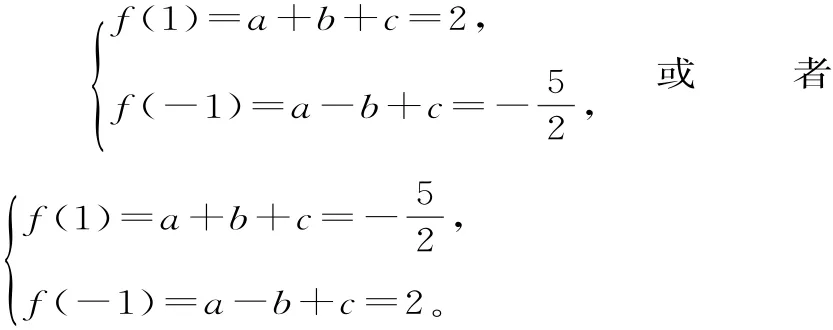
考點突破四、綜合法與分析法

考綱要求：了解直接證明的兩種基本方法:綜合法和分析法;了解綜合法和分析法的思考過程和特點。

權威解讀：分析法和綜合法是思維方向相反的兩種思考方法,當題目從題設不易入手,而從結論上較易打開思路時,多用分析法證明。我們在實際解題時,應把兩種方法結合起來運用,先用分析法尋求解題思路,再用綜合法有條理地表達解題過程,這就達到了揚長避短、相互協調、相得益彰的目的。

例6 (2017年山東文科卷)由四棱柱ABCD-A1B1C1D1,截去三棱錐C1-B1CD1后得到的幾何體如圖3所示,四邊形ABCD為正方形,O為AC與

BD的交點,E為AD的中點,A1E⊥平面ABCD。

(1)證明:A1O∥平面B1CD1;

(2)設M 是OD的中點,證明:平面A1EM⊥平面B1CD1。

解析：(1)取B1D1中點O1,連接CO1,A1O1,由于ABCD-A1B1C1D1為四棱柱,所以A1O1∥CO,A1O1=CO,因此四邊形A1OCO1為平行四邊形,A1O∥O1C。

又O1C?平面B1CD1,A1O?平面B1CD1,所以A1O∥平面B1CD1。

(2)因為AC⊥BD,E,M分別是AD,OD的中點,所以EM⊥BD。因為ABCD為正方形,所以AO⊥BD。又A1E⊥平面ABCD,BD?平面ABCD,所以A1E⊥BD。

因為B1D1∥BD,所以A1E⊥B1D1,EM⊥B1D1。

又A1E,EM?平面A1EM,A1E∩EM=E,所以B1D1⊥平面A1EM。

又B1D1?平面B1CD1,所以平面A1EM⊥平面B1CD1。

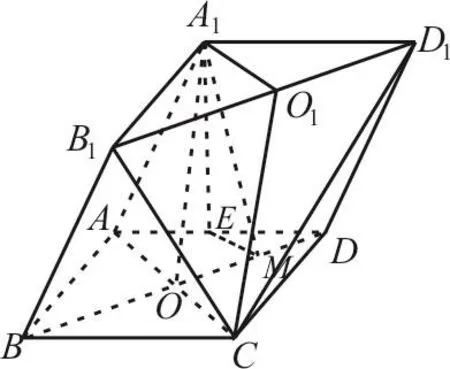
圖3

點評:綜合法是利用已知條件和某些數學定義、定理、公理等,經過一系列的推理證明,最后推導出所要證明的結論成立,這種證明方法叫作綜合法,又叫順推證法。它的基本思路是“由因導果”。

(1)求M;

(2)證明:當a,b∈M時,|a+b|＜|1+ab|。

綜上可得,M={x|-1＜x＜1}。

(2)當a,b∈(-1,1)時,有(a2-1)·(b2-1)＞0,即a2b2+1＞a2+b2。

則a2b2+2ab+1＞a2+2ab+b2。

整理得(ab+1)2＞(a+b)2,故|a+b|＜|ab+1|。

例7 (2017年全國Ⅱ卷)已知a＞0,b＞0,a3+b3=2,證明:

(1)(a+b)(a5+b5)≥4;

(2)a+b≤2。

解析：(1)(a+b)(a5+b5)=a6+ab5+a5b+b6=(a3+b3)2-2a3b3+ab(a4+b4)

=4+ab(a2-b2)2≥4。

(2)因為a＞0,b＞0,所以要證明a+b≤2,只需證明(a+b)3≤8,也即證明a3+3a2b+3ab2+b3≤8。

而a3+b3=2,只需證明a2b+ab2≤2。

而a2b+ab2-2=a2b+ab2-a3-b3=a2(b-a)-b2(b-a)=(a2-b2)(b-a)=-(b-a)2(b+a)≤0,此式顯然成立,故a+b≤2。

點評:分析法是從待證明的結論出發(fā),從“未知”看“需知”,漸漸靠攏“已知”,逐步尋找使它成立的充分條件,直至最后把要證明的結論歸結為判定一個明顯成立的條件,這種證明方法叫分析法。它的基本思路是“執(zhí)果索因”。

因為a⊥b,所以a·b=0。只需證明|a|2+|b|2-2|a||b|≥0,即(|a|-|b|)2≥0,得證。

考點突破五、數學歸納法

考綱要求：了解數學歸納法的原理,能用數學歸納法證明一些簡單的數學命題。

權威解讀：當遇到與正整數n有關的不等式證明時,應用其他辦法不容易證明,則可考慮應用數學歸納法證明。利用數學歸納法可以探索與正整數n有關的未知問題、存在性問題,其基本模式是“歸納—猜想—證明”,即先由合情推理發(fā)現結論,然后經邏輯推理即演繹推理論證結論的正確性。

例8 (2017年浙江卷)已知數列{xn}滿足:x1=1,xn=xn+1+ln(1+xn+1),n∈N*。

證明:當n∈N*時,

(1)0＜xn+1＜xn;

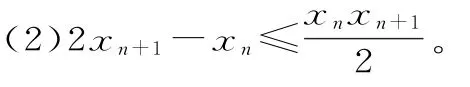
解析：(1)用數學歸納法證明xn＞0。

當n=1時,x1=1＞0。

假設n=k時,xk＞0。

那么n=k+1時,若xk+1≤0,則0＜xk=xk+1+ln(1+xk+1)≤0,矛盾,故xk+1＞0。

因此xn＞0,n∈N*。

因為xn=xn+1+ln(1+xn+1),因此0＜xn+1＜xn,n∈N*。

(2)由xn=xn+1+ln(1+xn+1)得:

xnxn+1-4xn+1+2xn=xn2+1-2xn+1+(xn+1+2)·ln(1+xn+1)。

記函數f(x)=x2-2x+(x+2)ln(1+x)(x＞0)。

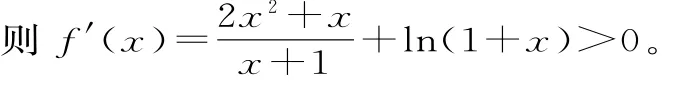
所以函數f(x)在(0,+∞)上單調遞增。

因此f(x)＞f(0)=0,xn2+1-2xn+1+(xn+1+2)ln(1+xn+1)=f(xn+1)≥0。

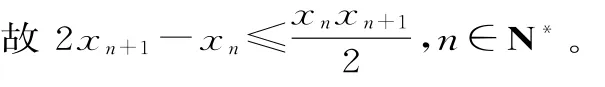
點評:應用數學歸納法證明不等式的關鍵是由n=k成立,證明n=k+1時也成立,證明時用歸納假設后,可采用分析法、綜合法、求差(求商)比較法、放縮法等證明。

跟蹤訓練9:(2018屆萊蕪實驗中學模擬)已知數列{an}的前n項和Sn滿足Sn=(1)求a1,a2,a3的值;(2)求{an}的通項公式。

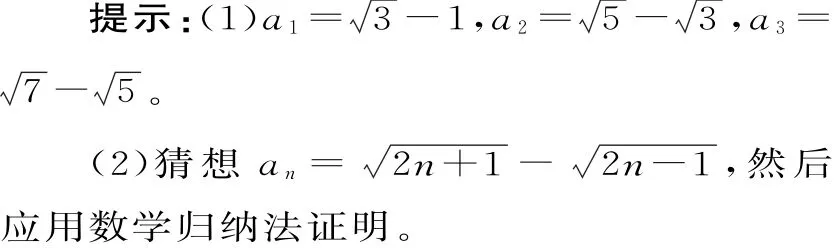
考點突破六、放縮法

考綱要求：了解放縮法的原理,能用放縮法證明一些簡單的數學命題。

權威解讀：放縮法是不等式證明中最重要的方法之一,放縮必須有目標,而且要恰到好處,目標往往要從證明的結論考查。常用的放縮方法有增項、減項,可利用分式的性質、不等式的性質、已知不等式,以及函數的性質進行放縮等。

例9 (2018屆成都七中月考)函數f(x)=ex-2ax,g(x)=ax2+1(a∈R)。

(1)設函數h(x)=g(x)-f(x),其導函數為h'(x),若h'(x)在[0,+∞)上具有單調性,求a的取值范圍;

解析：(1)h(x)=ax2+2ax-ex+1,h'(x)=2ax+2a-ex。

設u(x)=h'(x)=2ax+2a-ex,u'(x)=2a-ex。

若u'(x)=2a-ex≤0在[0,+∞)上恒成立,即2a≤ex在[0,+∞)上恒成立,則a≤

1;2

若u'(x)=2a-ex≥0在[0,+∞)上恒成立,即2a≥ex在[0,+∞)上恒成立,此時ex∈[1,+∞),故不存在a使得2a≥ex在[0,+∞)上恒成立。

所以h(x)在(0,+∞)上單調遞減,h(x)＜h(0)=0,即ex-x＞

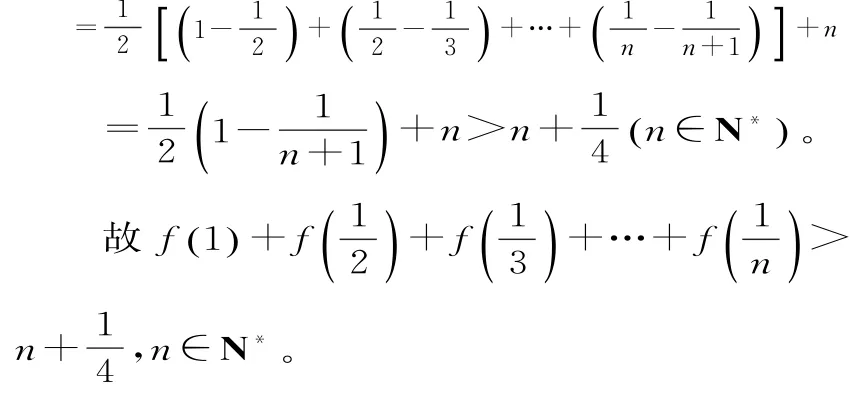
點評:在放縮法證明不等式的過程中,往往采用添項或減項的方法,放縮時要注意適度,否則不能同向傳遞。

跟蹤訓練10:(2016年四川卷)已知數列{an}的首項為1,Sn為數列{an}的前n項和,Sn+1=qSn+1,其中q＞0,n∈N*。

(1)若2a2,a3,a2+2成等差數列,求數列{an}的通項公式;

提示：(1)因為Sn+1=qSn+1,所以n≥2時,Sn=qSn-1+1。

兩式相減可得an+1=qan,即從第二項開始,數列{an}為等比數列,公比為q。

當n=1時,a1+a2=S2=qa1+1。

由于a1=1,a2=a1q=q,又2a2,a3,a2+2成等差數列,則2q+q+2=2q2,解得q=2或q=-