探析解決數列不等式問題的函數策略

浙江省紹興魯迅中學 (312000)

陳少春

數列是一個定義在正整數集(或其子集)上的特殊函數，它豐富了學生所接觸的函數概念的范圍，引導學生利用函數去研究數列問題，能使解數列的問題更有新意和綜合性，更能有效地培養學生的思維品質和創新意識.因此我們在解決數列問題時，可以從它的源頭、本質——函數的角度去解決它，充分利用函數的有關知識，以函數的概念、圖像、性質為紐帶，架起函數與數列之間的橋梁，揭示它們之間的內在聯系，比如數列的放縮、單調性可以借助函數的單調性方法放縮、判斷，數列的最大(小)項可以利用函數圖像的直觀性來比較，從而有效地解決數列不等式問題.下面筆者通過具體的例子嘗試從函數的角度處理數列不等式問題，希望對考生處理數列問題有些許幫助.

一、函數單調性處理數列遞推問題

數列和的不等式問題的矛盾在于數列相鄰兩項的遞推關系的發現，有時候從函數單調性角度去入手則事半功倍.

③綜上所述，該命題對所有的正整數n都成立.

(1)(2)證明略.

二、函數恒成立處理數列有界性、求和問題

找到數列任意兩項之間的關系，再分離變量轉化成函數恒成立問題是解決數列有界性的關鍵．

例3 (2016年浙江理20)設數列{an}滿足

(1)證明：|an|≥2n-1(|a1|-2),n∈N*；

|an|-2≥(|a1|-2)·2n-1，所以|an|≥

2n-1(|a1|-2),n∈N*.

例4 已知數列{an}的前n項和Sn，滿足an+Sn=1.

(1)求數列{an}的通項公式；

例5 已知數列{an}的前n項和Sn，滿足an+Sn=1.

(1)求數列{an}的通項公式；

三、函數圖像處理數列最值問題

函數圖像的直觀性可以為我們解決數列的最值問題帶來很多方便.

例6 (2012年浙江理7)設Sn是公差為d(d≠0)的無窮等差數列{an}的前n項和，則下列命題錯誤的是( ).

A.若d<0，則數列{Sn}有最大項

B.若數列{Sn}有最大項，則d<0

C.若數列{Sn}是遞增數列，則對任意的n∈N*，均有Sn>0

D.若對任意的n∈N*，均有Sn>0，則數列{Sn}是遞增數列

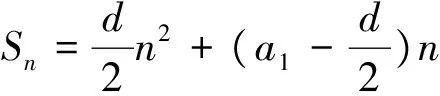
A.a1，a30B.a1，a9C.a10，a9D.a10，a30