國民經濟和科技投入水平之間的結構關系分析
——基于省級面板數據的Granger因果檢驗

丁 煜 李嘯虎

一、引 言

科技投入是衡量一個國家經濟持續發展和創新創業的主要引導力，它不僅有利于各國家了解其創新創業能力的高低情況，更有利于各國家提高和指導其創新創業能力。隨著我國改革開放的不斷深入，科技投入與經濟增長的評估也逐漸受到學者的關注。例如，張優智基于平滑轉換回歸（STR）模型分別研究了我國財政科技投入與經濟增長、R＆D經費投入與經濟增長的非線性關系，結果得到，中國經濟增長與科技投入之間存在顯著的非線性關系。再例如，祝云等借助協整回歸分析方法檢驗了中國經濟增長與科技投入的關系，進一步指出，財政科技投入與經濟增長之間存在顯著的互動關系，即兩者之間屬于相互拉動和相互影響的傳導機制。隨后，王凱等、張優智、凌江懷等借助VAR模型、協整檢驗、Granger因果檢驗等分析工具研究了中國經濟增長與科技投入的關系，重點通過方差分解和脈沖響應函數分析了兩者的長期均衡關系與短期動態關系，結果得到，中國經濟增長與科技投入之間存在顯著的均衡關系，并且伴隨一定的滯后效應。

但是值得注意的是，張優智、祝云、王凱、張優智、凌江懷等研究的結論大多基于科技投入中的R＆D經費投入指標，而沒有對科技投入的其他方面加以統計和測量，所以得到的研究結論并不能充分反映科技投入的程度，這樣得到的結論也只是單一指標對經濟增長的影響情況，并不能綜合研究科技投入與國民經濟增長之間的互動關系。對此，本文在上述學者研究的基礎上，引入科技活動的多個指標，用熵值法綜合得出科技投入水平的綜合指數，隨后將科技投入水平與國民經濟進行量化研究，并加入Cobb-Douglas方程、最小二乘法等分析工具，進一步分析科技投入水平與國民經濟之間的結構關系，進而為中國科技投入的差異化管理以及經濟政策的制定等方面提供理論的指導依據。這里進一步展開三個方面的研究工作：第一，對科技投入水平的指標進行界定，并通過熵值法對科技投入水平進行量化計算，得到各年的科技投入評價值；第二，在得到各年的科技投入評價值后，論文借助協整檢驗、ADF檢驗等分析工具研究中國經濟增長與科技投入水平之間的長期均衡關系，并通過Granger因果檢驗方法研究中國經濟增長與科技投入水平之間的短期均衡關系；第三，在得到科技投入與經濟增長之間的均衡關系后，論文加入Cobb-Douglas方程、最小二乘法等分析工具，進一步量化分析科技投入水平對經濟增長的影響程度；第四，簡要總結全文的研究結論，并提出相應參考建議。

二、科技投入水平測算

目前對于科技投入方面的指標選取沒有形成統一的界定，大多數文獻都是根據其研究的目的不同，定義不同的指標。例如，張優智在研究科技投入與經濟增長的關系上，主要以人均GDP作為經濟增長的代理變量，分別使用財政科技投入、R＆D經費投入作為科技投入的代理變量。張振剛等學者主要以人均GDP和科技研發經費STE進行換算。區域研究上也主要根據各區域數據得到，例如吳松強等在研究江蘇財政科技投入與經濟增長的關系時，數據指標以GDP作為因變量，以財政總支出、財政科技撥款、財政科技撥款／總支出、科技活動經費內部支出總額、R＆D支出作為自變量進行實證。所以本文考慮到研究的對象主要定位于科技投入水平，所以在構建指標的過程中論文以國家數據庫中的科技活動基本情況的相關指標為主，從規模以上工業企業R&D活動情況、規模以上工業企業新產品開發和生產情況、區域專利和有效發明情況以及技術市場情況四個方面選定11個指標構建出科技投入的指標體系。其中對于廢止的指標不與考慮（自2009年起廢止），主要包括科技活動人員指標、科學家和工程師人員指標、科技經費籌集額指標、政府資金的科技經費籌集額指標、企業資金的科技經費籌集額指標、金融機構貸款的科技經費籌集額指標、科技經費內部支出指標、科技活動人員、科學家和工程師人員經費籌集額、內部支出數據。論文研究的原始數據主要選擇1997年至2016年的年度數據。最終得到原始數據序列如表1所示。

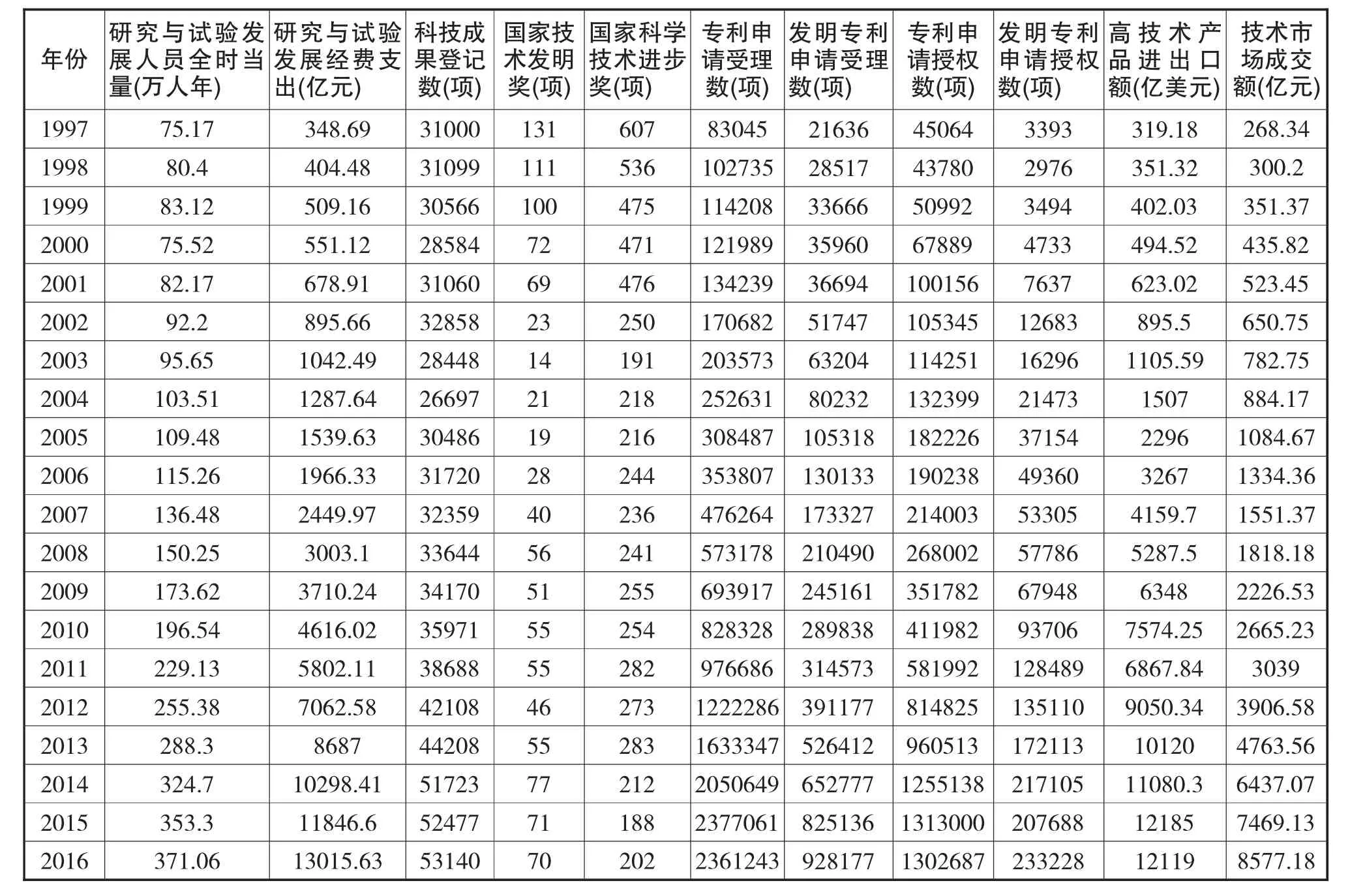
表1 原始數據序列

為有效解決多指標變量間的交叉問題，本文采用熵值法測算科技投入：（1）對原始數據Xij進行標準化，并將標準化的數據所在坐標系Zij平移幅度A（A可根據數據標準化分布的區間范圍確定）以保證數據的非負性，得到=Zij+A；（2）計算第 j項指標下第i年指標比重（3）計算第 j項指標熵值計算第j項指標權重wjpij。

論文根據構建的創新水平指標體系和確定的模型方法，從國家數據庫中搜集我國1997年至2016年的科技板數據，計算出各年的科技投入，定義為TC指數（如表2所示）；此外，加入GDP指數（國內生產總值（億元））進行對比分析，不難發現TC指數和GDP指數保持較好的同步性，具體如圖1所示。所以有必要對TC指數和GDP指數進行進一步分析，用以研究科技投入水平和經濟增長之間的關系。

表2 1997-2016年的TC指數與GDP指數

圖1 TC指數與GDP指數對比分析

三、科技投入水平與經濟增長的關系

依據經濟發展理論原理，科技投入水平與經濟增長之間存在兩種關系：第一種關系是科技投入水平對經濟增長的拉動作用或影響關系；第二種關系是經濟增長對科技投入水平的拉動作用或影響關系。所以這里為了檢驗兩者之間可能存在的兩種關系，論文首先將TC指數和GDP指數進行ADF檢驗，隨后通過協整關系檢驗兩者的長期均衡特征，再通過Granger因果關系檢驗兩者的短期均衡特征。數據由表2提供，樣本期為1997-2016年共20年的區間，同時需要對TC指數和GDP指數取自然對數以降低數據中可能存在的異方差性。

（一）平穩性檢驗

論文采用ADF方法分別將對數化的LTC指數和LGDP指數進行單位根檢驗，檢驗結果如表3所示。其中需要注意的是，序列dLGDP與序列dLTC分別是序列LGDP與序列LTC的一階差分；序列ddLGDP與序列ddLTC分別是序列LGDP與序列LTC 的二階差分；（c，t，k） 中 c，t，k 分別表示單位根檢驗中的截距項、時間趨勢項、最大滯后階數，k的選擇遵從最小AIC準則；在5%的水平下判斷序列是否平穩。軟件采用Eviews8.0，下同。

表3 序列LGDP和LTC的平穩性檢驗

由表3顯示的檢驗結果表明，結果如表2所示，原序列和一價差分后的序列在1%和5%的顯著水平上存在單位根（P值均大于0.05），說明都是非平穩的，而二價差分之后的序列在1%和5%的顯著水平上不存在單位根，說明是平穩的，即LGDP和LTC是二階單整序列。

（二）協整檢驗

上面已經檢驗了序列LGDP與序列LTC都屬于二階單整序列，所以論文可以采取Johansen協整檢驗進一步分析序列LGDP和序列LTC之間的長期均衡關系。Johansen協整檢驗可以選擇無截距項、無趨勢項、滯后1階，這樣便可以得到Johansen協整檢驗的最大特征值與秩檢驗，具體結果如表4所示。

表4 LGDP和LTC的Johansen協整檢驗

從表4所示的結果不難發現，序列LGDP與序列LTC協整檢驗所對應的P值都小于0.05，說明序列LGDP與序列LTC在5%水平上存在顯著的協整關系，可見，序列LGDP和序列LTC之間存在長期均衡關系。

（三）Granger因果檢驗

得到序列LGDP和序列LTC之間的長期均衡關系后，論文進一步通過Granger因果檢驗研究序列LGDP和序列LTC之間的短期均衡關系。考慮到序列LGDP和LTC都是二階差分平穩的，所以盡管經過處理后的序列是在原序列基礎上有所變動，但仍然保留了原序列的信息，因此可以采用LGDP和LTC的數據進行Granger因果檢驗。這里需要指出的是，兩者序列因果檢驗的滯后階數可以從1階取到6階，具體的檢驗結果如表5所示。

表5 dLGDP和dLTC的因果檢驗

根據表5所示的檢驗結果可以得到，從滯后1階取到滯后6階，科技投入水平都不是經濟增長的Granger原因（接受原假設），說明科技投入水平對經濟增長的拉動作用或影響關系不顯著，不能顯著影響經濟增長；但是當滯后1-2階以及之后5階時，經濟增長是科技投入水平的Granger原因（拒絕原假設），說明經濟增長對科技投入水平的拉動作用顯著，即經濟增長的變化會引起科技投入的顯著變化，反之則不成立。結合表5進一步得到，科技投入與經濟增長之間存在單向引導關系，即經濟增長對科技投入的單向拉動作用，并且這種單向引導作用具有一定的滯后性。

四、經濟增長對科技投入水平的影響分析

由于上述Granger因果檢驗方法的限制，無法進一步判斷經濟增長對科技投入水平的影響強度，所以論文接下來將引入Cobb-Douglas模型，量化分析經濟增長對科技投入水平的影響強度。

（一）模型、變量和數據說明

論文采用生產函數方法，將科技投入水平作為因變量，探討經濟增長對科技投入的影響強度。首先考慮Cobb-Douglas模型：

其中，Y(t)為t時刻的產出，K(t)為t時刻的資本投入，L(t)為t時刻的勞動投入，A(t)為t時刻的技術進步。將式（1）變換為對數形式，并將科技投入TC(t)加入到技術變化指標中，滿足：

最后得到如下線性回歸模型：

需要注意的是，式（4）中，產出Y(t-3)用國內生產總值GDP衡量，資本投入K(t)用全社會固定資產投資（億元）衡量。勞動力投入L(t)用經濟活動人口（萬人）衡量。科技投入水平TC(t)用第三節計算的結果加以衡量。實證數據為年度數據（從1997年至2016年），來源于國家數據庫（http://data.stats.gov.cn/index.htm）。

（二）實證分析

這里的模型估計主要通過最小二乘法進行估計，估計結果和相關統計量如表6所示的結果。

表6 經濟增長對科技投入水平影響的OLS估計結果

由表6可知，調整后的R2為0.977001，F統計量的P值為0.000000，說明自變量能很好地解釋因變量的變異程度，模型整體擬合效果較好；在顯著水平為0.05的情況下，各變量的系數通過了5%的顯著性水平。所以由最小二乘法估計模型（4）得到的回歸方程為：

lnTC(t)＝170.024＋0.439lnK(t)－16.55lnL(t)＋0.66lnY(t-3) （5）

該結果表明：1997-2016年間，經濟增長對科技投入水平的貢獻度為0.66，說明在其他因素保持不變的情況下，國民經濟每增長1%，相應的科技投入水平會增加0.66%。考慮到經濟增長可能會進一步拉動其他技術水平因素，進而拉動科技投入水平的提高，其貢獻部分會更大。

五、研究結論

在前人研究基礎上，本文通過ADF檢驗、協整檢驗、Granger因果檢驗以及Cobb-Douglas模型等分析工具研究了我國科技投入水平與經濟增長之間的關系，結果得到，科技投入水平和經濟增長之間存在長期的均衡關系。進一步研究得到，經濟發展是科技投入水平的Granger原因，并且經濟增長對科技投入水平的影響作用在一定時間后才可以呈現出來；相反，科技投入水平不是經濟增長的Granger原因。進一步地，從生產函數的最小二乘回歸估計顯示，1997-2016年間，經濟增長對科技投入水平的貢獻度為0.66，即其他因素保持不變的情況下，國民經濟每增長1%，相應的科技投入水平會增加0.66%。值得注意的是，論文得到的結論與張優智、凌江懷等研究的結論不相同（財政科技投入是經濟增長的格蘭杰原因），這主要在于論文采取的指數數據與其他學者的研究數據不同。所以，從宏觀角度來看，有必要對科技投入進行差異化管理，同時不斷提升國民經濟水平，這樣才能為科技投入提供更多資源。

【參考文獻】

［1］劉國新，馮德雄，姚漢軍，等.區域創新創業能力的綜合評價.武漢理工大學學報.信息與管理工程版.2003.25（1）84-88

［2］張優智.我國科技投入與經濟增長的動態關系研究.科研管理.2014.35（9）58-68

［3］祝云，畢正操.我國財政科技投入與經濟增長的協整關系. 財經科學.2007（7）53-59

［4］王凱，龐震.中國財政科技投入與經濟增長：1978-2008.科學管理研究.2010.28（1）103-111

［5］張優智.財政科技投入與經濟增長的協整檢驗.科技進步與對策.2012.29（7）11-16

［6］凌江懷，李成，李熙.財政科技投入與經濟增長的動態均衡關系研究.宏觀經濟研究.2012（6）62-68

［7］張優智.科技投入與經濟增長:存在門限的非線性關系.中國科技論壇.2014（5）32-38

［8］張振剛，田帥，陳志明.科技投入與經濟增長的互動機制研究—基于珠三角地區靜態和動態面板數據的實證研究. 科學管理研究.2010.28（5）89-93

［9］吳松強，陳雅雯，鄭垂勇.江蘇財政科技投入與經濟增長的關系研究.科學管理研究.2015.33（1）72-75.

［10］劉翠.我國上市商業銀行競爭力研究.甘肅金融.2013（03）53-56

［11］Johansen S.Statistical analysis of cointegration vectors.Journal of Economic Dynamics and Control. 1988.12:231-254

［12］梁小珍，陸鳳彬，李大偉，等.工程建設標準對我國經濟增長影響的實證研究——基于協整理論、Granger因果檢驗和嶺回歸.系統工程理論與實踐.2010.30（5）841-847