基于數據驅動的風力發電機組獨立變槳距載荷優化控制

， ，

(1. 蘇州工業職業技術學院 電子與通信工程系， 江蘇 蘇州 215104；2. 江南大學 物聯網工程學院，江蘇 無錫 214100； 3.蘇州富強科技有限公司， 江蘇 蘇州 215010)

風機因其不確定性和強非線性，建模難度大，傳統的設計方法不能準確體現它的特點，目前自適應和魯棒性反饋控制方法也不能解決模型誤差帶來的一系列問題。文獻[8-9]中提到的數據驅動優化技術為風電系統載荷優化控制器的設計提供了一種新的思路，該方法僅依靠輸入輸出數據獲得系統的最優控制器，可以解決復雜的具有不確定關系的實際控制系統建模難度大的問題[10-13]。

為了實現風力發電系統的載荷優化控制，本文中對風力發電機組獨立變槳控制技術進行研究，將數據驅動與最優控制結合，根據系統的輸入輸出數據，在馬爾科夫參數基礎上構建了狀態觀測器，提出了基于數據的風力發電機組獨立變槳距最優控制，有效緩解了風機槳葉及其他關鍵部件的疲勞載荷。

1 基于數據的獨立變槳距最優控制設計

獨立變槳距所要實現的最優控制目標主要有2個：1)保持電機轉速和輸出功率近似為定值；2)通過減小傾斜以及偏航疲勞載荷，保證系統具有良好的穩態和動態性能。

系統的輸入和測量輸出定義為

(1)

y(k)=(ΔMtilt(k) ΔMyaw(k) ΔΩh(k) ΔP(k))T,

(2)

在k時刻系統的狀態方程和輸出方程[15]為

(3)

式中：x(k)為系統的n維狀態向量；u(k)為l維控制向量；y(k)為m維輸出向量；A、B、C分別為m×n、n×l、m×n型時變矩陣。

獨立變槳距的指標函數達到最小值時，可以實現最優控制，該值可以利用u(k)計算得到，指標函數J的求解公式為

(4)

式中R、Q為m×m型正定對稱的加權矩陣。

根據分離原理，可以求解出系統最優控制的解，求解方法[16]為

u(k)=L(k)xc(k)

,

(5)

式中：L(k)為最優控制器；xc(k)為狀態向量。它們可表示為

L(k)=-[R+Ψ(k+1)TΦ(k+1)Ψ(k+1)]-1·

Ψ(k+1)Φ(k+1)，

(6)

xc(k)=(CACA2…CAN-k)Tx(k)，

(7)

Ψ(k+1)=C(k+1)B=(M1M2…MN-k)T，

(8)

Φ(k+1)=Q(k+1)-Q(k+1)H(k+1)[R(k+1)+

H(k+1)TQ(k+1)H(k+1)]-1H(k+1)T·

Q(k+1)，

(9)

(10)

R(k+1)=diag(R,R,…,R)

,

(11)

Q(k+1)=diag(Q,Q,…,Q)

，

(12)

式(10)中：Mi=CA(i-1)B,i=1, 2, …,N為系統的馬爾可夫參數；當k+1=N時，H(k+1)=0。R(k+1)、Q(k+1)均為N-k個分塊的對角矩陣。

2 馬爾科夫參數的獲取與狀態向量的估計

考慮系統(3)迭代p(p≥0)步可得

(13)

式中：up(k)、yp(k)分別為以u(k)、y(k)為初始的p組輸入、輸出數據；Ap為n×n型時變矩陣；Bp為n×pl型可控矩陣；Cp為pm×n型可觀矩陣；Dp為pm×pl型托布里茲矩陣，它是根據馬爾科夫參數組成的。具體的表達式如下：

(14)

引理1[17]設系統(13)是可觀測系統，當pm≥n， 就存在矩陣M滿足

Ap+MCp=0

。

(15)

把M代入可移除系統(13)的狀態變量，可得

(16)

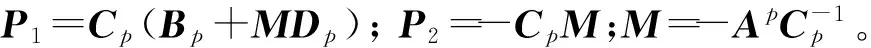
根據式(17)、(18)將輸入輸出數據列向量構成矩陣Y和V，可由Y和V得到方程(19)[18]，

Y=(yp(k+p)yp(k+p+1)…yp(k+p+L))，

(17)

(18)

(P1DpP2)=YVT(VVT)-1。

(19)

參數P1、P2及Dp可根據式(19)得到。 當p=N+1時， 根據Dp的表達式可以得到馬爾科夫參數。為了確保該參數精確，V數據中行向量線性無關[19]，所以Y、V中的數據要有足夠的長度。

通過式(13)、(16)可以估計控制器狀態向量。

xc(k)=(0IN-k)Cpx(k)=

(0IN-k)[P1up(k-p)+P2yp(k-p)]，

式中：IN-k為N-k階單位矩陣；p=N-k+1。

(20)

由以上可以得到數據驅動的獨立變槳距控制策略結構(見圖1)。數據驅動實現控制目標的步驟如下：1)根據輸入輸出數據獲得馬爾科夫參數；2)進行行向量狀態估計，得到系統的輸入變量；3)控制獨立變槳距系統。

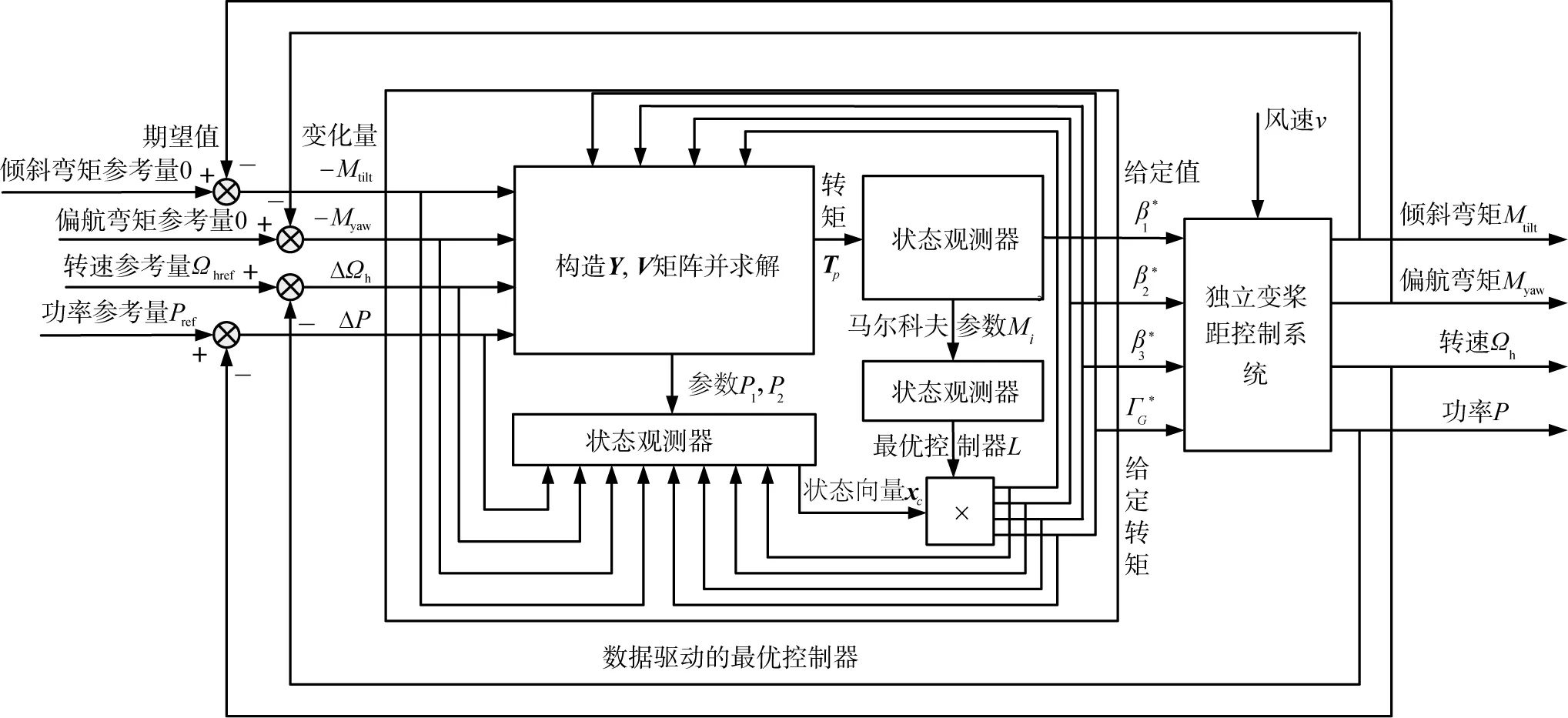
圖1 數據驅動的獨立變槳距控制策略

3 建模與仿真分析

3.1 獨立變槳距控制系統仿真模型

建模是為了模擬系統運行數據，構建用于數據驅動的輸入輸出數據來源，其系統結構圖如2所示。

根據葉素動量理論，傳動機構、塔的動態方程及槳葉根部彎矩為[4]

(21)

(22)

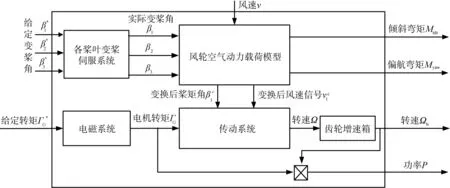
圖2 獨立變槳控制框圖 Mzi=hMzvi+kMz βi-hMzxfa

(23)

式中：J為風機的轉動慣量；Ω為風輪轉速；βi為各槳葉的槳距角(i=1,2,3)；vi為各槳葉上的等效風速；Mx為橫向的葉片揮舞力矩；Fx為橫向為葉片揮舞力；Mz為縱向的葉片揮舞力矩；hMx為橫向葉片揮舞力矩與風速的系數；kMx為橫向葉片揮舞力矩與槳距角的系數；hFx為橫向葉片揮舞力與風速的系數；kFx為橫向葉片揮舞力與漿矩角的系數；hMz為縱向葉片揮舞力與風速的系數；kMz為縱向葉片拍打力矩與槳距角的系數[20]；xfa為塔架頂部前后方向移動的位移；Tg為發電機轉矩；Mz,i為槳葉縱向的葉根彎矩信號；M、D、S分別為塔的質量、剛度系數和阻尼系數；φi為第i個槳葉方位角。設風力機第一個槳葉的方位角為φ，則第i個槳葉的方位角為

傾斜彎矩Mtilt和偏航彎矩Myaw根據葉根彎矩和傾斜彎矩、偏航彎矩之間的關系可表示為

(24)

由上式可知，這是一個多輸入多輸出的系統，為實現風機線性化控制器設計，通過多葉片坐標變換可以消除風機葉輪周期旋轉對系統的影響，從而將該時變系統模型轉換成線性定常系統模型。基于方位角的數學模型不僅包含風輪軸及其葉片的狀態變量，還包含風輪轉速Ω。因為轉速Ω具有同軸方向；所以無需進行轉換，但是有效風速、偏航彎矩及傾斜彎矩等狀態變量需要進行變換，即通過Coleman坐標變換的P變換實現，

(25)

其逆變換為

(26)

利用Coleman坐標變換將時變系統轉換成線性定常系統，得到了葉輪轉速Ω、塔頂運動、偏航彎矩及傾斜彎矩的傳遞函數。線性定常模型為

(27)

(28)

(29)

(30)

(31)

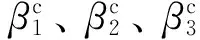
3.2 仿真分析

本文中選取1臺風輪直徑為103.6 m、切出風速為25 m/s的風機進行仿真實驗，該風機的功率為2.5 MW，輪轂中心高為90 m，風機葉輪的額定轉速為14 r/min。在MATLAB/Simulink仿真平臺中搭建變速變槳風能轉換系統的模型，獨立變槳距最優控制器的驅動是通過S-Function編制數據實現的。

由于系統需要采樣得到一定量的數據，因此初始為開環狀態。在該狀態下將采樣時間設置為0.001 s， 只需0.2 s系統就能獲取到充足的樣本數據， 然后對目標進行控制。 進行仿真實驗時所用到的參數如下：N=8,P=N+1=9,L=3P+10=37,Q=I4×4。

圖3所示為風速的仿真曲線，圖4—6所示分別為發電機的轉矩、 轉速和功率曲線， 圖7為槳葉1、2、3的變槳角曲線，圖8—9分別為輪轂處的傾斜彎矩曲線、偏航彎矩曲線。

圖3 風速仿真曲線

圖4 風力發電機轉矩曲線

圖5 風力發電機轉速曲線

圖6 風力發電機功率曲線

圖7 風力發電機槳葉1、2、3變槳角曲線

圖8 風力發電機輪轂處傾斜彎矩曲線

圖9 風力發電機輪轂處偏航彎矩曲線

由圖3—6可以看出， 當風速大于額定值時， 采用基于數據驅動的風電機組獨立變槳距方法可以使得發電機的功率、 轉矩和轉速分別穩定在額定值2.5 MW、 200 kN·m及125 rad/s附近。仿真結果表明，系統的振蕩明顯減小，并且運行也更加穩定，這證實了本文控制策略的有效性。

在此基礎上，針對系統疲勞載荷問題，本文中將基于數據驅動的獨立變槳距控制技術與統一變槳距控制技術進行對比研究。

分析圖7的仿真波形可知，采用獨立變槳距控制技術時，風輪掃過平面會因為受到風剪切的影響而進行調節，使得每個槳葉的變槳角呈周期性變化。

由圖8—9可知，基于數據驅動的獨立變槳距控制能有效減小在輪轂處的傾斜彎矩和偏航彎矩，表明獨立變槳距控制下的系統載荷彎矩較統一變槳距控制下的系統載荷彎矩有明顯的減小。傳動系統、塔架等的疲勞載荷會隨著輪轂處的載荷彎矩減小而減小，因而提高了系統的性能，延長了系統的使用壽命。該控制策略與統一變槳距控制相比，優化效果更明顯。

4 結語

在基于模型的最優控制分析基礎上，本文中提出了基于數據驅動的風力發電機組獨立變槳距的最優控制。在未知模型的基礎上，僅利用采樣得到的輸入輸出數據對各槳葉變槳角及發電機的轉矩進行控制，從而實現風力發電機組獨立變槳距載荷優化控制。仿真結果表明，當風速大于額定風速時，采用數據驅動的獨立變槳距最優控制使發電機的輸出功率穩定在額定值附近，而且系統具有良好的穩定性，與統一變槳距控制相比較，該控制策略明顯減小了風力發電機槳葉及其他關鍵部件的疲勞載荷。

參考文獻:

[1] SELVAM K. Individual pitch control for large scale wind turbines: technical report: ECN-E-07-053[R]. Energy Research Center for the Netherlands (ECN)，The Netherlands，2007.

[2] SIM C, BASU S, MANUEL L. On space-time resolution of inflow representations for wind turbine loads analysis[J]. Energies, 2012, 5(7):2071-2092.

[3] KONG Y G，GU H. Load analysis and power control of large wind turbine based on wind shear and tower shadow[J]. Journal of Southeast University，2010，40(1)：228-233.

[4] 左姍, 王磊, 宋慶旺,等. 基于載荷優化的漂浮式海上風力發電機組變槳距控制研究[J]. 太陽能學報, 2015, 36(9):2292-2299.

[5] 應有，許國東. 基于載荷優化的風電機組變槳距控制技術研究[J]. 機械工程學報，2011，47(16):106-111.

[6] BOSSANYI E. Further load reductions with individual pitch control[J]. Wind Energy，2005，4(8): 481-485.

[7] SELVAM K, KANEV S, WINGERDEN J W, et al. Feedback-feed forward individual pitch control for wind turbine load reduction[J]. International Journal of Robust and Nonlinear Control，2009，19(1): 72-91.

[8] WANG T, GAO H, QIU J. A combined adaptive neural network and nonlinear model predictive control for multirate networked industrial process control[J]. IEEE Trans on Neural Netw Learn Syst, 2015, 27(2):416-425.

[9] CAMPI M C，SAVARESI S M. Direct nonlinear control design：the virtual reference feedback tuning(VRFT) approach[J]. IEEE Transactions on Automatic Control，2006，51(1)：15-27.

[10] 朱遠明. 基于參數化控制器的數據驅動控制方法研究[D]. 北京：北京交通大學, 2014.

[11] VIVEIROS C, MELICIO R, IGREJA J M, et al. Performance assessment of a wind turbine using benchmark model: fuzzy controllers and discrete adaptive LQG[J]. Procedia Technology, 2014, 17:487-494.

[12] MAHMOUD M S, ALYAZIDI N M, SAIF A W A. LQG control design over lossy communication links[J]. International Journal of Systems Science, 2013, 45(11):2309-2326.

[13] ZHANG J, ZHANG H, WANG B, et al. Nearly data-based optimal control for linear discrete model-free systems with delays via reinforcement learning[J]. International Journal of Systems Science, 2014, 47(7):1-11.

[14] 馬忠鑫. 大型風力發電機組獨立變槳距控制方法研究[D]. 無錫：江南大學，2013.

[15] 張羽飛, 馮汝鵬, 王茂.H2/H∞混合優化問題綜述[J]. 信息與控制, 2002, 31(5):430-436.

[16] NUDELL T R, CHAKRABORTTY A. Graph-theoretic methods for measurement-based input localization in large networked dynamic systems[J]. IEEE Transactions on Automatic Control, 2015, 60(8):2114-2128.

[17] AZEEM S A, AHMED H. Effective technique for the recognition of offline Arabic handwritten words using hidden Markov models[J]. International Journal on Document Analysis and Recognition, 2013, 16(4):399-412.

[18] 徐莉莉, 紀志成. 數據驅動的風能轉換系統最優控制[J]. 南京航空航天大學學報,2012, 44(1): 129-133.

[19] FAZEL M, PONG T K, SUN D, et al. Hankel matrix rank minimization with applications to system identification and realization[J]. SIAM Journal on Matrix Analysis and Applications, 2013, 34(3):946-977.

[20] BOTTASSO C L, CROCE A, GUALDONI F, et al. Load mitigation for wind turbines by a passive aeroelastic device[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2016, 148:57-69.