從一題多解談向量問(wèn)題的解決方法
鄒司偉
(江蘇省蘇州實(shí)驗(yàn)中學(xué) 215000)
本文利用“一題多解”的理念,從不同角度分析解決一道習(xí)題,旨在幫助學(xué)生總結(jié)歸納向量問(wèn)題的常用解法,激發(fā)學(xué)生的學(xué)習(xí)興趣、培養(yǎng)學(xué)生勇于探索的習(xí)慣和敢于創(chuàng)新的能力.

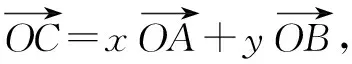
一、向量分解法
設(shè)∠COA′=α,利用正弦定理得到:

=2cos(60°-α).
于是α=60°時(shí)x+y取最大值2.
或者使用余弦定理:
注意到∠CA′O=60°,從而得到等式:x2+y2-1=xy.
利用基本不等式易得x+y的最大值為2.
二、建系求解法
如圖3建立坐標(biāo)系:
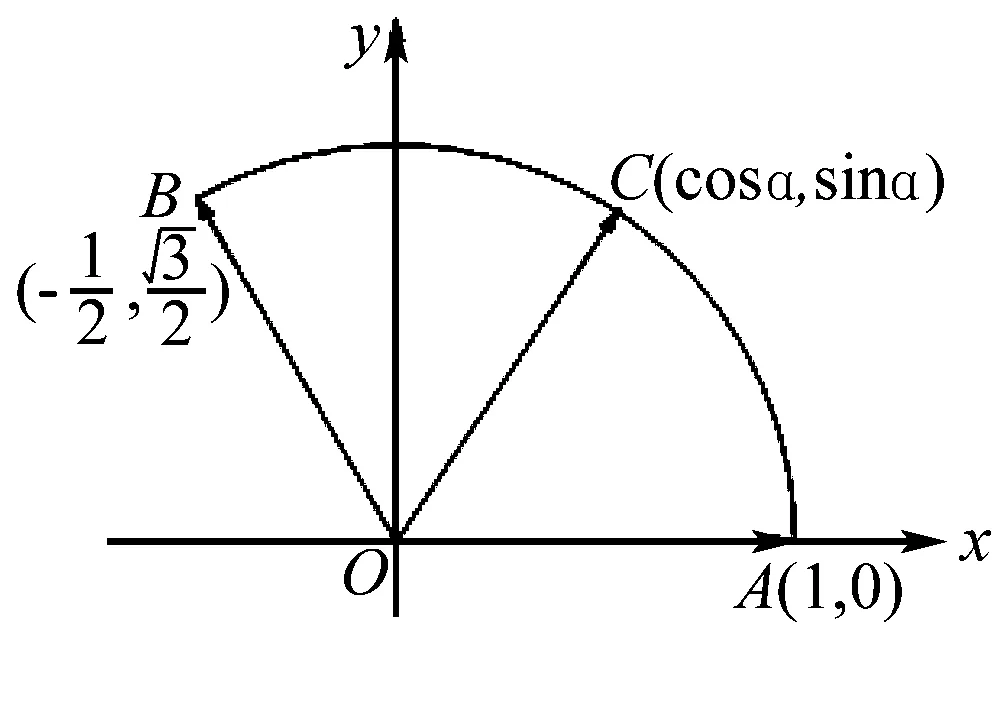
由題意得
解得:

易知當(dāng)α=60°時(shí),x+y取最大值2.
三、內(nèi)積求解法
如果從向量?jī)?nèi)積角度出發(fā),我們可以通過(guò)內(nèi)積的方法,將向量等式轉(zhuǎn)化為數(shù)量等式,從而求解問(wèn)題.

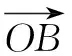
之后步驟類似方法二.
四、幾何解法
而向量問(wèn)題往往可以有幾何解釋,我們利用等和線的知識(shí)可以得到另一個(gè)解法:
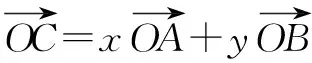
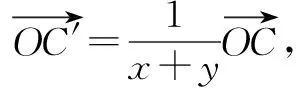
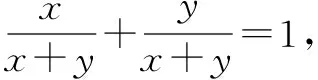
作出圖形:


本題的幾種解法中,解法一,四比較依賴圖形的幾何性質(zhì),而解法二,三更偏向于代數(shù).

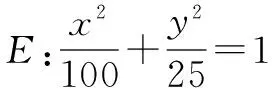
本題將圓替換為橢圓,圓的優(yōu)良的幾何性質(zhì)丟失了,從而用向量分解或者幾何轉(zhuǎn)化的方法都解決不了.而通過(guò)坐標(biāo)系或者內(nèi)積,將問(wèn)題代數(shù)化仍然有效.

觀察問(wèn)題,發(fā)現(xiàn)題目中有關(guān)鍵詞“外心”,從而由外心的幾何性質(zhì),聯(lián)想到使用內(nèi)積的方法將問(wèn)題代數(shù)化后就能有效解決.

參考文獻(xiàn):
[1] 任燕.淺談一題多解應(yīng)注意的問(wèn)題[J].速讀旬刊,2016(10).
[2] 張軒.小議高中數(shù)學(xué)中的一題多解[J].魅力中國(guó),2016(18).

