淺談阿波羅尼斯圓在高中幾何的應用

曾信源

(浙江省溫州市龍灣中學高二(9)班 325024)

阿波羅尼斯圓在我們的教材習題以及課外練習中經常出現，甚至有些難題如果我們能夠看到它背后命題的本質是阿波羅尼斯圓，那么就會給我們解題帶來很大的方便.

一、引例

解析設點M(x,y)，由條件直接列出等式，經化簡不難得到點M的軌跡方程是(x+1)2+y2=4，顯然點M的軌跡是一個圓.

這是我們數學必修2教材《圓的方程》的一道課后習題，如果把以上的題目推廣到一般情形那么就是阿波羅尼斯圓.其實在教材的復習參考題中，是以如下表述形式出現的：

已知點M(x,y)與兩個定點M1,M2距離的比是一個正數m，求點M的軌跡方程，并說明軌跡是什么圖形(考慮m=1和m≠1兩種情形).

我們按照引例的方法建立恰當直角坐標系，就能得到這個圓的方程(m≠1).這個知識點在平面幾何和立體幾何都有廣泛應用.

二、阿波羅尼斯圓在平面幾何的應用

解析這是2008年江蘇省的一道高考題，如果按照解三角形的知識去處理，運算會顯得很繁瑣.如果這道題我們建系去解決，會發現本題的命題背景就是阿波羅尼斯圓.

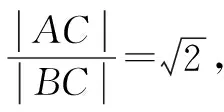
三、阿波羅尼斯圓在立體幾何的應用

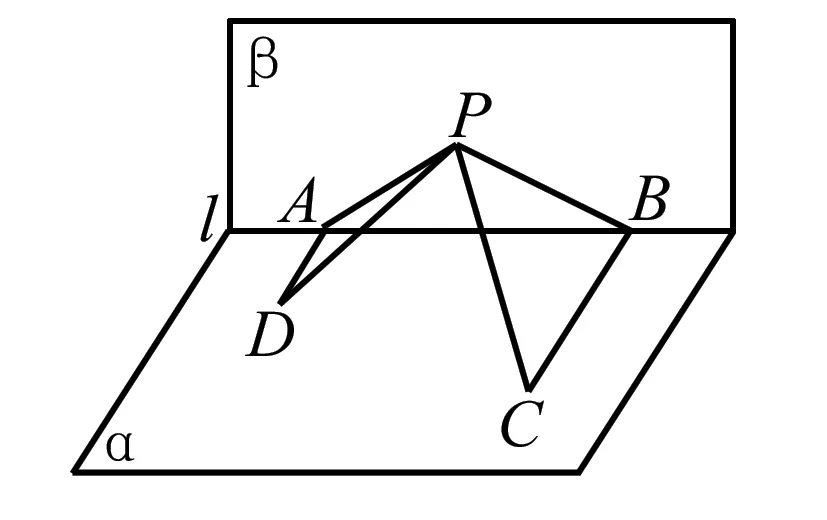
圖1

例3 如圖，平面α⊥平面β,α∩β=l,DA?α,BC?α,且DA⊥l于A,BC⊥l于B，AD=4，BC=8，AB=6，在平面β內不在l上的動點P，記PD與平面β所成角為θ1，PC與平面β所成角為θ2，若θ1=θ2，則△PAB的面積的最大值是 .

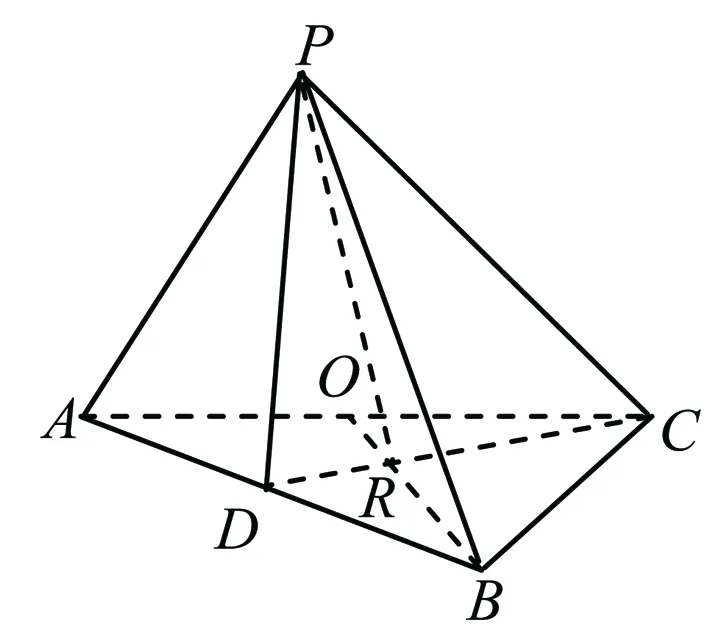
圖2

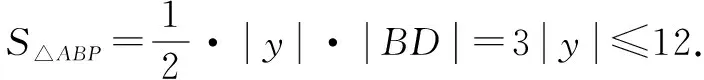
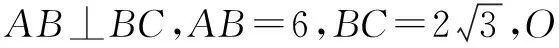
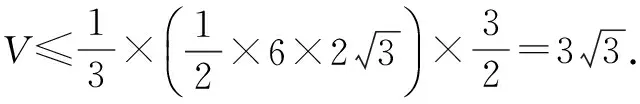
變式練習2 已知平面ABCD⊥平面ADEF，AB⊥AD,CD⊥AD，且AB=1,AD=CD=2.

ADEF是正方形，在正方形ADEF內部有一點M，滿

足MB,MC與平面ADEF所成的角相等，則點M的軌跡長度為( ).

提示點M的軌跡是阿波羅尼斯圓，答案為C.

總之，通過以上例題的深刻分析，我認為在平時的數學學習中，如果我們懂得去發現和總結規律，那么我們數學學習就會顯得格外輕松，從而能領悟數學的真諦與魅力.

參考文獻：

[1]人民教育出版社.普通高中課程標準實驗教科書數學必修2教師教學用書[M].北京：人民教育出版社，2007.