以形助數 數形結合
周小微
(江蘇省江安高級中學 226500)
數形結合思想是解數學題時常用的思想方法,可以把某些抽象的問題直觀化,把抽象思維變為形象思維,從而利于把握數學問題的真諦.
一、數形結合,巧解方程
眾所周知,方程自身或方程兩邊(或通過變形)的表達式有明顯的幾何意義,對于一些無法直接解決的方程問題,如果采用數形結合的思想,將抽象的數量關系轉化為圖形來解決,可以事半功倍地解決問題.
例1 實數p取什么值時,方程|x2-4x+3|=px有四個不同的實數根?
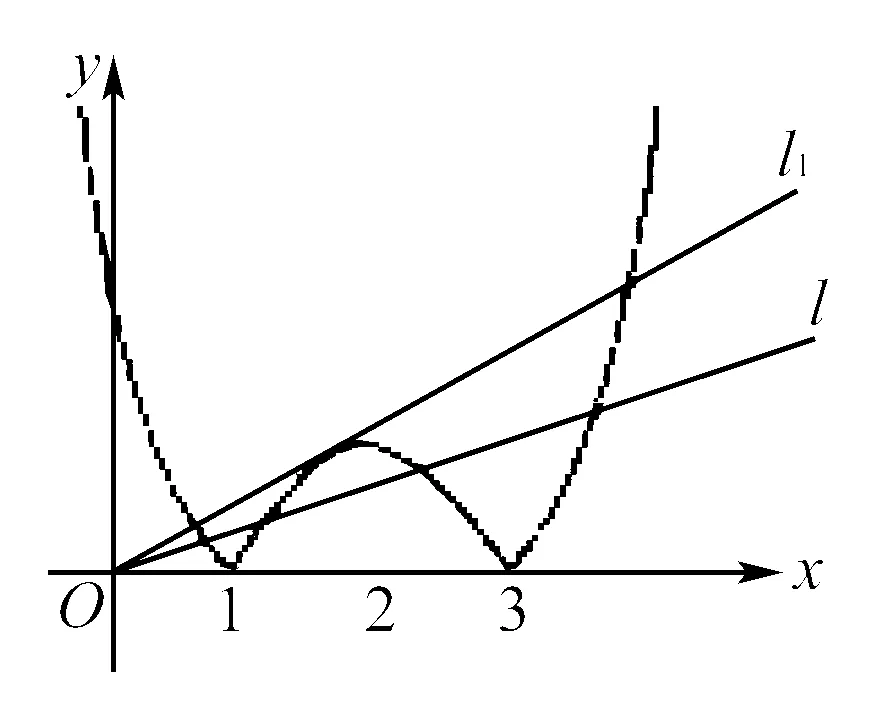
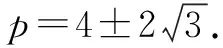
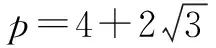
點評本題中的方程有明顯的幾何意義,即所構造的y=|x2-4x+3|與y=px兩條曲線的交點的個數即為方程的實數根的個數.
二、數形結合,速求極值
三角函數是函數部分的一個重要內容,可以充分利用數形結合思想來研究其性質,把圖象和性質結合在一起,即能夠利用圖象的直觀性得出函數的性質,也能利用函數的性質來描繪函數的圖象,這樣既可以掌握函數的圖象和性質,又可以熟練地利用數形結合的方法.
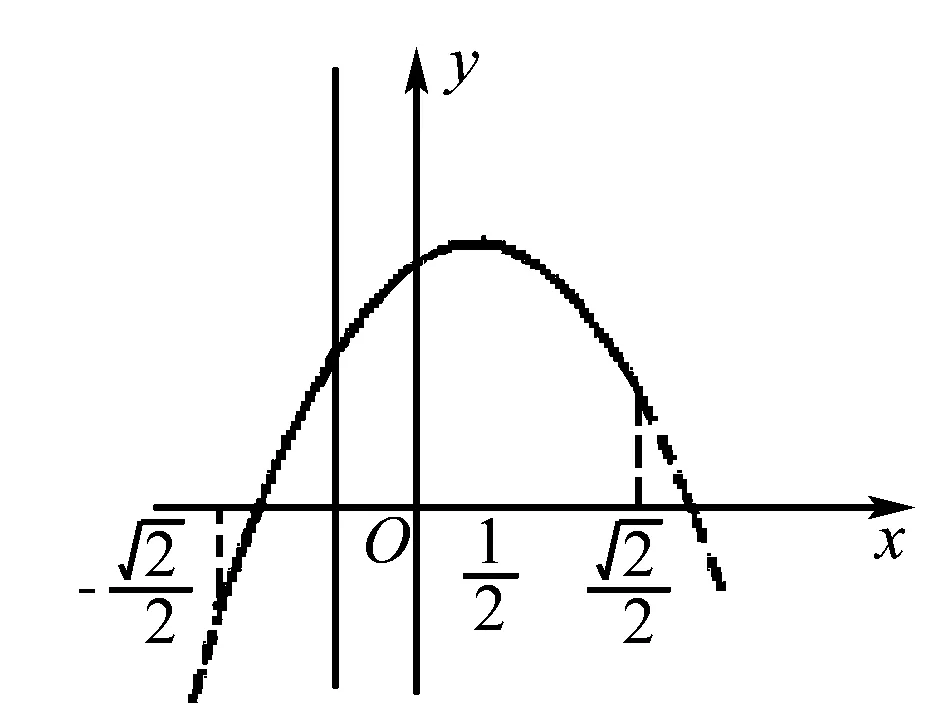
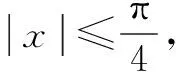
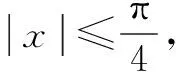
點評本題中三角函數的圖象為數形結合帶來了便利條件,從圖象上尋找滿足條件的定義域,找到對應的函數值常常是解決問題的關鍵.
三、數形結合,轉化復數
數形結合法是解復數問題的常用方法,能夠把復數問題變為幾何問題,從而能夠降低解題難度.用此方法解復數問題時要把握好復數的特征,充分認識到復數與幾何、函數之間的關系,利用數形結合對復數問題進行轉化,從而直接、快速地求解.
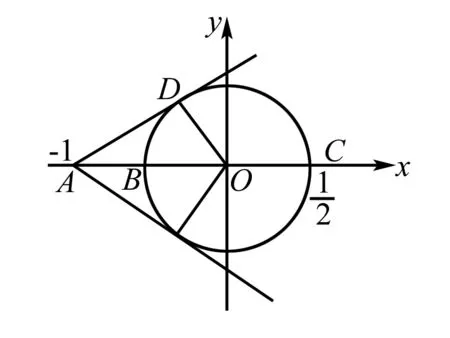

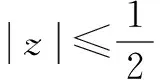
點評本題是利用復數在復平面內對應的圖形及其幾何意義來解題的.其幾何意義包括與復平面內的點一一對應,還有與復平面內從原點出發的向量一一對應,因此可以從解析幾何的角度來審視復數問題,可借助數形轉換來解題.
四、數形結合,證明不等式
不等式問題一直是高考中的高頻考點,而證明不等式的方法有很多,有基本不等式法、函數法等.運用數形結合法來證明不等式,透過不等式的性質發現其幾何意義,構造相應的幾何圖形來闡述不等式,將抽象問題具體化,直觀化.
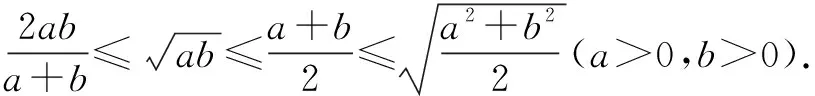
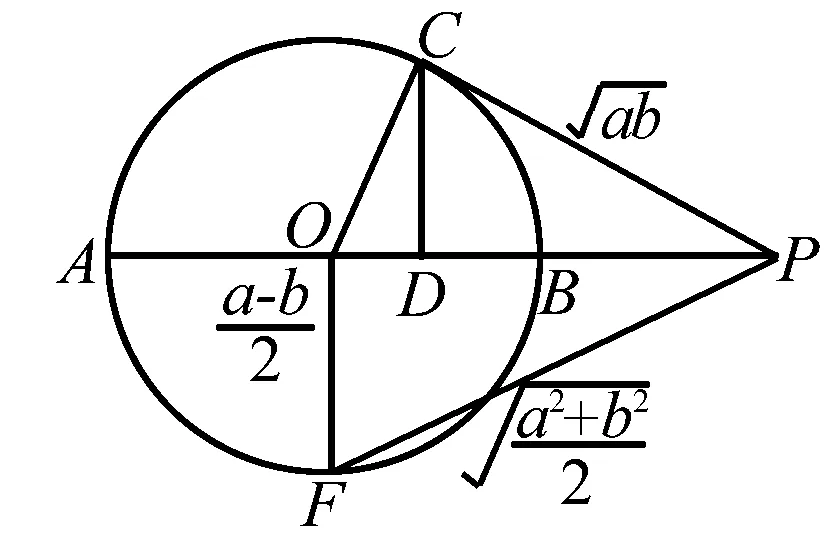
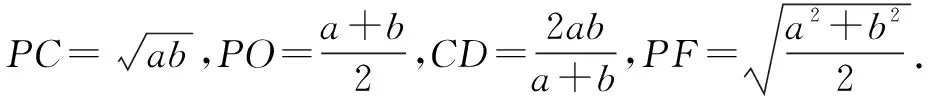
點評本題可以采用兩種思路,從兩種角度進行解題分析.一是采用基本不等式法,將不等式拆分,逐個進行證明;二是采用數形結合的方法,通過構造不同的平面的圖形,從圖形的角度直觀化進行不等式證明.
數形結合方法可以用來解答各種難題,包括一些復雜函數的極值問題、方程問題、復雜的集合問題等等.在高中數學的教學過程中,應該立足教材,挖掘數學思想方法,從而優化教學內容,在講解題目的過程中適當的介紹數形結合思想方法,提高學生解題能力.
參考文獻:
[1]呂福剛.數形結合方法在數學教學中的應用探究[J].教育現代化,2017(34).
[2]王林.高中數學教學中數形結合方法的有效運用[J].科學大眾(科學教育),2017(09).

