常見能量表達式中的慣性含義
吳書含
(中央民族大學附屬中學 100081)
能量是物理學中十分重要的概念,描述著物質世界的運行規律,隱含著研究對象的性質和信息.從能量入手可以深刻地理解物理規律的本質.在高中階段我們接觸過多種能量,很多都是在變化過程中產生并積累的,例如質點運動動能、彈簧彈性勢能、電容器靜電場能和自感線圈中自感磁能.我們可以運用功能轉化關系并借助做功數值導出其表達式.不過,在能量積累過程中研究對象的狀態可能變化,類似恒力做功公式W=FScosθ這類恒定條件過程的結論是否適用需要討論.對這類問題,我們通常將完整過程分解為無數個小段,即使從整體來看物理量是變化的,但是在小段內由于所涉及的時間和空間均很小,這些物理量可近似不變,高中階段的公式和經驗在特定小范圍內可以應用.整個過程又可以看成是這些小段的積累,將全部小段內做功相加即得到全過程做功,再借助功能轉化關系可以求出能量的表達式.在這種“微元法”的思維下,高中常見能量表達式得到了研究,并指出了各能量表達式中隱含的慣性含義.
一、質點的動能
描述質點機械運動的能量稱為動能,當質點速度為零時動能為零,而當質點速度不為零時,其表達式可以通過動能定理得出.動能定理指出質點動能改變量等于外力做功大小.外力既可能是恒力也可能是變力,若將整個過程分解為無窮多小段,在每一小段中均可認為外力大小恒定,則第n段中外力做功可表述為
ΔWn=FnΔsn
其中Fn是第n段中外力的大小,Δsn是第n段的小位移,數值趨于零.根據牛頓第二定律
其中an、Δvn和Δtn分別是第n段的加速度、速度改變量和時間,Δvn和Δtn均趨于零但比值不為零.第n段做功改寫為
vn為第n段內質點的速度,由于Δvn趨于零,vn近似為常數.畫出mv-v的圖象得到一條斜率為m的直線,如圖1所示.
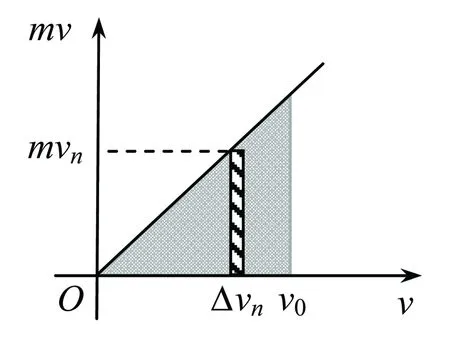
圖1
將v=0至v=v0范圍分成無窮多份,第n份中圖象與橫軸圍成小長方形且面積為mvnΔvn,與第n段外力做功數值相等.其他小段結論與第n段結論相似.若初始時質點速度為零,外力作用后末速度為v0,則對于整個過程,外力做功大小等于每一小段做功之和,數值等于所有小段對應面積之和,即與圖中標示的三角形面積數值相等.整個過程外力做功為

除了動能,常見的能量還有彈簧彈性勢能、電容器中靜電場能以及自感線圈中自感磁能.下面利用與討論動能相同的方法推導它們的能量表達形式,并揭示它們包含的各種形式的“慣性”.
二、彈簧彈性勢能
一端固定的彈簧,另一端受到沿彈簧軸線方向的外力作用而發生形變,其內部有彈力的作用,具有彈性勢能.輕質彈簧緩慢伸長過程中,外力做功數值等于彈性勢能增加量.對于輕質彈簧緩慢伸長這一情況,外力大小與彈簧彈力大小相等,外力是一個變力,其做功不能應用恒力做功公式.如果將這一過程分解為無窮多個小段,每一小段彈簧伸長量趨于零,在小段內彈力可以近似為常量.第n段外力做功表示為
ΔWn=FnΔxn
其中Fn是第n段中外力的大小,Δxn是第n段形變量,數值趨于零.根據胡克定律Fn=kxn,第n段做功改寫為
ΔWn=kxnΔxn
畫出kx-x的圖象將得到斜率為k的直線,與圖1的圖象類似.仿照動能討論,將kx-x圖象橫軸分解為無窮多小份,其中第n份圖象與橫軸圍成的面積為kxnΔxn,與第n段外力做功數值大小相同.對于彈簧從原長緩慢伸長到形變量為x0這一狀態,外力做功數值與這個形變范圍內圖象與橫軸圍成的面積相同,表述為
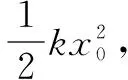
三、電容器中的靜電場能
對于電容為C,初始兩極板不帶電的電容器,經外力做功搬運電荷使兩極板間產生電勢差U0.外力做功轉化為電容器存儲的靜電場能,通常取初始電勢差為零時靜電場能為零.欲推導靜電場能的表達式,需求解該過程中外力做功,再利用功能轉化關系求得.隨著兩極板間電勢差逐漸增大,外力搬運相同電荷所做的功不同.若將整個過程分解為無數個小段,在每一小段中兩極板電勢差變化量趨于零,兩極板電勢差近似不變.在第n段中,外力做功
ΔWn=UnΔqn
其中Un是第n段內兩極板間電勢差,Δqn為該段內搬運的電荷量,根據電容的定義式得出Δqn=CΔUn,ΔUn為該段內電勢差改變量趨于零.代入第n段做功表達式得出
ΔWn=UnΔqn=CUnΔUn
畫出CU-U的圖象將得到一條斜率為C的直線.與前方討論類似,若將橫軸分成無數個小份,第n份中圖象與橫軸圍成的面積等于第n段外力做功大小.對于初狀態不帶電,末狀態兩極板間電勢差為U0的電容器,外力在整個過程中做功大小等于在橫軸相應范圍內圖象與橫軸圍成的總面積

四、自感線圈中的自感磁能
自感線圈由于自感作用,線圈中電流變化會產生自感電動勢,若線圈中電流由初始為零增大到末狀態I0的過程中,電荷通過線圈需克服線圈自感電動勢做功,該過程使得電荷的能量轉化為線圈的自感磁能.在電流逐漸變大的過程中,相同時間內通過的電荷量不同,轉化為自感磁能的數量不同.將整個過程分解為無窮多個小段,每一小段中電流改變量趨于零,電流近似為常量.但是在相同的小段內時間也趨于零,趨于零的電流改變量與趨于零的時間比值不為零,即自感電動勢不為零.第n段中電荷通過線圈克服自感電動勢做功
ΔWn=εnΔqn

畫出LI-I的圖象將得到一條斜率為L的直線.與前方討論類似,將橫軸分成無窮多份,第n份中圖象與橫軸圍成的面積等于第n段做功數值.對于電流由初始狀態為零增大到末狀態為I0的過程,電荷克服自感電動勢做功等于圖象與橫軸圍成的總面積

五、總結

參考文獻:
[1] 李剛.彈性勢能表達式的推導方法[J].中學物理教學參考,2007,36(6):12.
[2] 袁俊.探究電容器中的能量計算問題[J].中學物理,2015,33(3):62.
[3] 程稼夫.中學奧林匹克競賽物理教程電磁學篇[M].合肥:中國科學技術大學出版社,2014:450-453.

