世界大學排名比較中的再認啟發式和線索推斷*

高山川 王 燕

(復旦大學心理學系，上海 200433)

1 引言

在信息有限的情境下，個體只能依據少量線索作推斷。Goldstein和Gigerenzer(2002)發現，利用簡單的再認也可做出準確的判斷，如果只能再認兩個選項中的一個，就推測它有更大的目標值(如聽說過的城市有更多人口)，他們稱此策略為再認啟發式(recognition heuristic；簡稱RH)。RH之所以有效，是因為再認與預測目標存在相關。不少研究證實RH能較好預測被試的選擇且正確率較高，涉及領域有城市人口(劉敏，張慶林，2006)、股票投資(Borges，Goldstein，Ortmann，& Gigerenzer，1999)、體育比賽(Herzog & Hertwig，2011)及選舉(Gaissmaier & Marewski，2011)，但也有少數例外(Oppenheimer，2003)。Goldstein和Gigerenzer(2002)還認為，RH對再認的利用是非補償性的：個體無需搜索其它線索，或即使知道相矛盾的線索，仍傾向于選擇可再認對象。不過有學者認為個體會綜合考慮其它線索，采用的是補償性策略(Oeusoonthornwattana & Shanks，2010；Pohl，2011)。對此，Gigerenzer和Goldstein(2011)總結了研究的一些誤區，強調個體并不盲目選用RH，會對再認的有效性作評估：再認效度較高時，能否再認是優先考慮的線索，反之則轉向其它更有效線索。他們還指出，實驗的選項應隨機抽取，要考察個體自然的再認記憶和線索知識。另外，以往研究中與選項有關的線索知識需在實驗中學習(如有聯賽球隊的城市通常人口更多)，易產生期望效應(Pachur，Br?der，& Marewski，2008)，也未充分利用個體現成的常識。

其實，與生涯決策有關的學校選擇問題可為RH研究提供合適材料。大學的名氣是學生擇校的一大依據(王長旺，2008)。大學名稱可提示額外信息，如位于中國還是外國(如哈佛大學)或學科專長為何(如倫敦商學院)，用這些線索也可推斷學校的實力。一些組織定期發布世界大學排名，可作為評判學生對學校的認知是否準確的依據。例如高等教育研究機構Quacquarelli Symonds編制的QS世界大學排名，包括了世界大學的綜合實力排名和各類專業的50強排名(劉強，潘鵬飛，王玉清，2015)。隨著越來越多中國大學生熟知的本土大學登上該榜單，了解中外大學在其心目中的排名很有意義。盡管大學生信息有限，若能充分利用環境中的線索，仍能表現出生態理性(Arkes，Gigerenzer，& Hertwig，2016)。

研究選擇了三種大學排名比較任務考察大學生利用RH和額外線索作推斷的情況。首先檢驗如下假設：不同任務中被試選擇可再認對象的比率及其正確率有顯著差異。然后分析在不同的學校配對中被試如何利用再認和其它線索作推斷。最后探討再認線索的非補償性，即存在額外的有利或不利線索時，被試選擇可再認對象的比率是否發生變化。研究既能增進對RH的認識，還可為改善外部環境、引導大學生的選擇提供參考。

2 方法

2.1 被試

被試為某大學公選課的208名本科生，平均年齡19歲(s=1.37)。男生69人(33%)，女生134人(65%)，不詳5人(2%)；一年級117人(56%)，二年級48人(23%)，三年級18人(9%)，四年級17人(8%)，不詳8人(4%)；人文社科類專業111人(54%)，理科類42人(20%)，經濟管理類29人(14%)，醫科類21人(10%)，不詳5人(2%)。

2.2 材料和程序

采用問卷調查法，任務包括選擇和再認。在選擇部分，羅列了兩兩配對的大學名稱，要求被試估計每對中哪一個在特定的大學排名范疇中名次更靠前并打勾；在再認部分，隨機列出了所有學校名稱，要求被試在那些參與調查前就聽說過的校名前打勾，沒聽過的打叉。大學排名分為三類：綜合實力、商業與管理專業(簡稱商科專業)、農業與林業專業(簡稱農林專業)。學校名稱來自QS世界大學排名(2016-2017)：對商科專業、農林專業的50強全部納入比較；對綜合實力排名中的學校，從前150名中隨機抽取50所(外國大學名稱翻譯參照教育部教育涉外監管信息網http：//www.jsj.edu.cn/n1/12018.shtml)。每一類的學校配對過程相同：先由電腦程序把50所大學兩兩隨機配對，共1225對組合，從中隨機抽取50對(50所大學中的每一所至少出現一次)。每人比較三個類別共150對學校。所有學校名稱打亂后隨機排列構成再認名單，共有122所不同大學(一些學校在不同類別中都有出現)。問卷還作了平衡處理：選擇與再認任務出現的先后不同，分為先再認、后選擇和先選擇、后再認；三個比較類別出現的先后也不同。最后形成8個版本的問卷，對被試隨機發放，要求當場完成，不能查詢外部信息，無時間限制。回收有效問卷208份，8個版本人數大致相當。

采用被試內設計，自變量為三種大學排名比較類別，因變量為被試選擇可再認對象的比率及其正確率。用SPSS20.0軟件進行數據統計分析。

3 結果

初步分析未發現再認與選擇任務的先后或比較類別的先后對因變量有順序效應，故以下呈現所有被試的結果。被試的選擇是否正確參照了QS世界大學排名。

3.1 描述性統計

綜合實力、商科專業、農林專業這三種排名各50對學校的名次差距平均值依次為52名(s=35)、16名(s=12)、16名(s=13)，差距較明顯，有利于被試作比較。根據每個被試再認的結果統計其在每種任務中的基本數據：RU配對數為只有一個選項被再認的配對數；再認正確預測次數為可再認對象是正確答案的次數；再認選擇次數為被試選擇了可再認對象的次數；再認選擇正確次數為被試選擇了可再認對象且符合正確答案的次數。按如下公式算出每個被試的四個指標：

RU占比=RU配對數/ 50

再認效度=再認正確預測次數/ RU配對數

再認選擇率=再認選擇次數/ RU配對數

再認正確率=再認選擇正確次數/ 再認選擇次數

再認選擇率常被作為推定個體使用了RH的指標。此外統計了每個被試在每種排名比較中的總正確率和能再認的學校比率。表1列出了所有被試在三種比較任務中上述指標的平均數和標準差。

表1 三種排名比較中主要指標的平均數與標準差(N=208)

表1顯示，被試在綜合實力和商科專業排名比較中總正確率較高，均超過60%。再認效度(α)因類別而異，在綜合實力排名比較中較高接近70%，在商科和農林專業排名比較中接近猜測的正確率50%。再認選擇率及其正確率在綜合實力和商科專業排名比較中都較高。跨類別的相關分析發現α與再認選擇率有顯著相關，r=0.45，p<0.001，α與再認正確率也有顯著相關，r=0.69，p<0.001。

3.2 不同排名比較任務中利用再認的差異

對表1中三種排名比較的再認選擇率及其正確率分別進行重復測量方差分析，結果發現：比較類別對再認選擇率的主效應顯著，F(2，207)=134.92，p<0.001，ηp2=0.40；比較類別對再認正確率的主效應也顯著，F(2，207)=138.74，p<0.001，ηp2=0.40。對三種任務的再認選擇率及其正確率分別進行配對樣本t檢驗，結果發現：綜合實力與商科專業排名比較相比，被試在前一任務中再認選擇率更高，t(207)=8.28，p<0.001，d配對=0.42，再認正確率也更高，t(207)=7.75，p<0.001，d配對=0.51；綜合實力與農林專業排名比較相比，被試在前一任務中再認選擇率更高，t(207)=14.05，p<0.001，d配對=0.97，再認正確率也更高，t(207)=16.32，p<0.001，d配對=1.11；商科專業與農林專業排名比較相比，被試在前一任務中再認選擇率更高，t(207)=9.61，p<0.001，d配對=0.41，再認正確率也更高，t(207)=8.70，p<0.001，d配對=0.61。上述差異檢驗的效應量根據胡竹菁和戴海琦(2017)的公式求得，顯然比較類別對再認選擇率及其正確率產生了很大影響，綜合實力與農林專業排名比較之間的差異尤其明顯。

3.3 再認線索與外國線索的預測比較

被試僅再認學校配對中的一個時，推斷可再認的大學排名靠前，此時的決策依據稱為再認線索。兩所學校均能或不能再認時，只好察看有無其它線索或猜測。將被試的選擇在多大程度符合特定線索的預測稱為線索的預測率，對照正確答案算出線索正確率。在綜合實力排名比較的50對學校中，有14對為一中一外大學配對(簡稱中外配對，如南京大學與高麗大學)，其中有9對的外國大學排名比中國大學靠前，據此得到一條預測效度為0.64(即9/14)的線索，即不考慮其它信息，只要是外國大學，就推斷其排名靠前，將其稱為外國線索。根據每個被試對這14對學校的再認情況算出各人的再認效度，平均為0.51(s=0.11)。在商科專業排名比較的50對學校中，有15對為中外配對(如北京大學與美國西北大學)，其中有13對的外國大學排名比中國大學靠前，此時外國線索的預測效度達0.87(即13/15)。根據每個被試對這15對學校的再認情況算出各人的再認效度，平均為0.31(s=0.19)。在農林專業排名比較的學校中只有一所中國農業大學，故不作分析。表2列出了兩種排名比較中只涉及中外配對時再認和外國線索的預測結果分析。

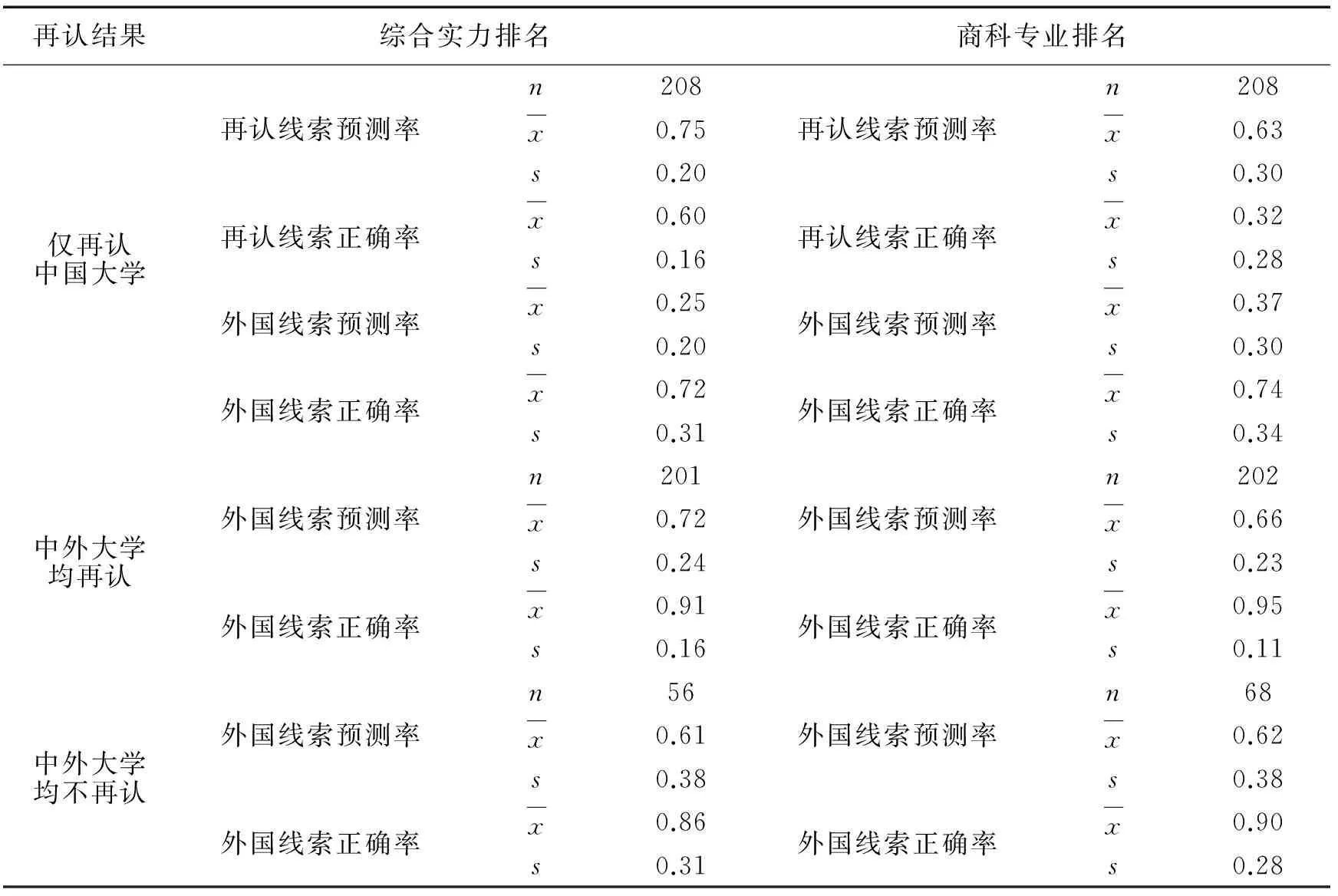
表2 中外配對比較中再認和外國線索的預測結果之平均數和標準差

注：由于被試對學校配對的再認情況不同，表中的n會有所變化(下同)

表2顯示，無論是綜合實力還是商科專業排名比較，被試只能再認學校配對中的中國大學時，其選擇都更多符合再認線索預測，但正確率有較大差距。被試無法利用再認線索時(均再認或均不能再認)，外國線索的預測率大大增加且正確率較高。

3.4 再認線索與專長線索的預測比較

在專業排名比較中，除再認線索外，另一可供利用的線索為大學是否以學科專長來冠名，可稱為專長線索。在商科專業排名比較的50對學校中，有9對為一所商科冠名大學與另一所非商科冠名大學的配對(簡稱有無冠名配對，如倫敦商學院與杜克大學)，且全是外國大學(另有兩對由于包括中國大學，會摻雜其它線索，不參與分析)。在這9對學校中有6對為商科冠名大學的排名靠前，專長線索的預測效度為0.67。根據每個被試對這9對學校的再認情況算出各人的再認效度，平均為0.21(s=0.24)。在農林專業排名比較中，有11對學校配對中包含一個以農業冠名的學校，但該專長線索的預測效度較低為0.36，故不作分析。表3列出了在商科專業排名比較中再認和專長線索的預測結果分析。

表3 有無冠名配對比較中再認和專長線索的預測結果之平均數和標準差

表3顯示，學校配對中不被再認的大學名稱顯示了專長線索時，被試不再偏向于選擇能再認的大學，兩條線索的作用持平，但專長線索的正確率遠超再認線索。被試無法利用再認線索時，專長線索的預測率大大增加但正確率波動較大。

3.5 再認線索的非補償性

研究還分析了存在額外的有利或不利線索時被試選擇可再認對象的比率是否變化。這需要把綜合實力和商科專業排名中的學校配對比較分成三種情境：只有再認線索時標記為RU情境，多一條不利線索時標為R-U情境，多一條有利線索時標為R+U情境(下面用數字1代表外國線索，2代表專長線索)。在綜合實力和商科專業排名比較中，中外配對各為14、15對，被試只能再認其中的中國大學時，外國線索與再認線索預測相反，此時前者為不利線索(標記為R-U1情境，下面以此類推)，被試只能再認其中的外國大學時，外國線索與再認線索預測一致，此時前者為有利線索(R+U1)；兩所外國大學的配對(簡稱二外配對)各為35、23對，此時只有一條再認線索(RU)。在商科專業排名比較中，還有9對為有無商科冠名的大學配對，被試只能再認其中的無冠名大學時，專長線索與再認線索預測相反，此時前者為不利線索(R-U2)，被試只能再認其中的有冠名大學時，專長線索與再認線索預測一致，此時前者為有利線索(R+U2)；前述23對二外配對大學均無商科冠名，只有一條再認線索(RU)。在算出兩種排名比較中上述各情境下的再認效度和再認線索預測率后，將二者的關系用圖1描繪出來。

圖1顯示，無論是綜合實力還是商科專業排名比較，多出一條外國線索時，即R+U1情境與RU情境相比，再認線索預測率是接近的，配對樣本t檢驗未發現顯著差異，t(36)=1.16(p>0.05)、t(72)=1.43(p>0.05)。無論是綜合實力還是商科專業排名比較，R-U1情境與RU情境相比，前一情境下的再認線索預測率顯著低于后者，t(207)=-7.89(p<0.001，d配對=0.53)、t(205)=-8.14(p<0.001，d配對=0.58)；但這兩種情境下再認線索預測率的絕對值不低，分別為75%、63%。在商科專業排名比較中，多出一條專長線索時，即R+U2情境與RU情境相比，再認線索預測率有顯著差異，t(133)=4.94，p<0.001，d配對=0.50，但該R+U2情境下再認效度高達0.93；R-U2情境與RU情境相比，前一情境下再認線索預測率也顯著低于后者，t(189)=-10.30，p<0.001，d配對=0.73，但該R-U2情境下的再認效度僅為0.21，在如此不利的情況下再認線索預測率仍不低于50%。

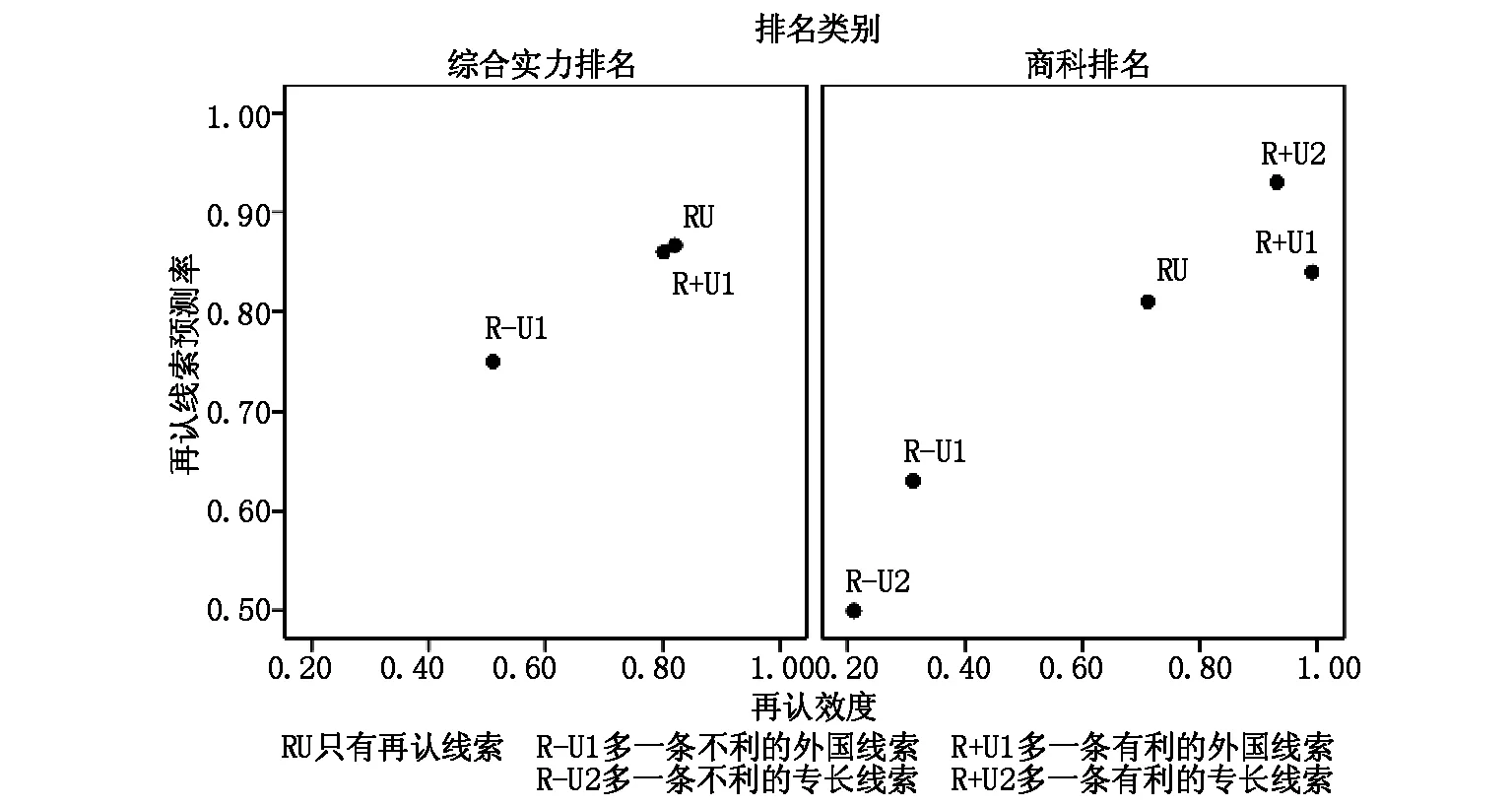
圖1 兩種排名比較任務中不同情境下的再認效度和再認線索預測率

4 討論

4.1 再認效度對利用RH的影響

被試對可再認對象的選擇率因不同任務而異，不同任務的再認效度(α)又不一樣。在α較高的任務中，再認選擇率及其正確率也較高；在α不高的任務中，再認選擇率及其正確率都明顯降低。這與前人的結果一致，Pohl(2006)發現，被試在推斷瑞士城市人口規模(α=0.86)時較符合RH的預測，在推斷城市與瑞士中心的距離(α=0.51)時則不然。Gigerenzer和Goldstein(2011)總結出α與再認選擇率的相關為0.57。研究中二者相關也顯著，為0.45。另一發現是，即便是對同一領域的三種任務，被試也不會不加區別地利用RH，可見他們對再認有效性的評估較為細致，覺察到了知名大學的單科排名不一定靠前。根據Goldstein和Gigerenzer(2002)的推算，α大于0.5時用RH做決策是有生態理性的。綜上，在生涯決策領域同樣有適合RH的用武之地。

4.2 信息有限時對額外線索的利用

研究中學校配對是隨機的，卻出現了兩條可供被試利用的額外線索(外國線索、專長線索)，各有一定的預測效度。通過分析被試在不同學校配對中的表現可見，再認效度較低或無法利用再認時，被試的選擇在不同程度符合外國線索或專長線索的預測。正如Gigerenzer和Goldstein(2011)所言，盡管再認是一條默認線索，個體不會忽略其它有用信息。研究中商科排名比較的α不到0.5，可能正是因為被試從再認轉向了其它線索，總正確率才能超過60%。上述三條線索并不能解釋被試所有的選擇，未來可繼續發掘個體利用的更多線索。

4.3 再認線索的非補償性

即使存在額外線索，再認的利用仍可能是非補償性的。一方面，在兩種排名比較的R-U情境下，再認預測率介于50%～75%，不利線索會明顯降低但無法消除被試對再認對象的選擇，尤其是在α較高的情境下，這跟前人發現一致(Pachur et al.，2008)。另一方面，R+U情境下出現了不同結果：多出一條外國線索時，無論哪種排名比較，被試對再認對象的選擇比率未顯著超過RU情境；但多出一條專長線索時，93%的被試選擇了能再認的商科冠名大學。不過由于后一種R+U情境下再認效度高達0.93，被試的選擇依然可能只是基于再認，而非綜合考慮專長線索的結果。前人有關R+U的發現也不太一致(Oeusoonthornwattana & Shanks，2010；Pachur et al.，2008)。未來可聯系不同情境下的線索效度來分析個體對線索的加工策略。

5 結論

(1)被試在綜合實力和商科專業排名比較中的正確率均超過60%，選擇可再認學校的比率及其正確率也較高；(2)比較類別對再認的選擇率及其正確率均有顯著影響，效應量很大；(3)在再認效度較低或無法利用再認的學校配對比較中，被試的選擇在不同程度符合外國線索或專長線索的預測；(4)多出一條不利線索時，被試選擇可再認學校的比率比只有再認線索時明顯降低但不低于50%，多出一條有利線索時，被試選擇可再認學校的比率因線索而異。

胡竹菁，戴海琦.(2017).心理學實驗研究的效果大小.心理學探新，37(1)，70-77.

劉敏，張慶林.(2006).推理的再認啟發模式研究.心理科學，29(6)，1354-1358.

劉強，潘鵬飛，王玉清.(2015).變革中的大學學科排名——QS 世界大學學科排名最新進展與反思.比較教育研究，311(12)，35-41.

王長旺.(2008).大學排名現象分析及應對方案.當代教育論壇，(4)，72-73.

Arkes，H.R.，Gigerenzer，G.，& Hertwig，R.(2016).How Bad Is Incoherence?Decision，3，20-39.

Borges，B.，Goldstein，D.G.，Ortmann，A.，& Gigerenzer，G.(1999).Can ignorance beat the stock market?In G.Gigerenzer，P.M.Todd，& the ABC Research Group，Simpleheuristicsthatmakeussmart(pp.59-72).New York：Oxford University Press.

Gaissmaier，W.，& Marewski，J.N.(2011).Forecasting elections with mere recognition from small，lousy samples：A comparison of collective recognition，wisdom of crowds，and representative polls.JudgmentandDecisionMaking，6，73-88.

Gigerenzer，G.，& Goldstein，D.G.(2011).The recognition heuristic：A decade of research.JudgmentandDecisionMaking，6，100-121.

Goldstein，D.G.，& Gigerenzer，G.(2002).Models of ecological rationality：The recognition heuristic.PsychologicalReview，109，75-90.

Herzog，S.M.，& Hertwig，R.(2011).The wisdom of ignorant crowds：Predicting sport outcomes by mere recognition.JudgmentandDecisionMaking，6，58-72.

Oeusoonthornwattana，O.，& Shanks，D.R.(2010).I like what I know：Is recognition a non-compensatory determiner of consumer choice?JudgmentandDecisionMaking，5，310-325.

Oppenheimer，D.(2003).Not so fast!(and not so frugal!)：Rethinking the recognition heuristic.Cognition，90，B1-B9.

Pachur，T.，Br?der，A.，& Marewski，J.N.(2008).The recognition heuristic in memory-based inference：Is recognition a non-compensatory cue?JournalofBehavioralDecisionMaking，21，183-210.

Pohl，R.F.(2011).On the use of recognition in inferential decision making：An overview of the debate.JudgmentandDecisionMaking，6，423-438.