基于ARIMA模型對我國升學率的研究

張燕妮

為分析近幾年我國教育部門高中升學率的變動趨勢，并預測未來幾年的升學率情況，為今后教育事業的發展提供相應對策建議。文章采取1990-2012年的教育部門高中升學率數據建立ARIMA模型，利用2013年度數據檢驗模型的預測精度，利用最終模型預測2014年的升學率。通過EVIEWS對序列進行檢驗估計，最終選擇ARIMA（（5，6，8），2，（7））疏系數模型對序列進行分析預測。研究結果表明，我國升學率呈現一個先增加后下降的趨勢，但是增加的幅度超過降低的幅度。2014年的升學率預測值為84.5%。

ARIMA模型 升學率 預測

前言

在當今的教育形勢下，教育的任務不單單是傳道和解惑，升學率也成為一個學校的主要追求目標，這彰顯了一個學校的地位。升學率可以說是應試教育的產物，一個學校的吸引力就在于升學率的高低，這可以說是一個學校的“招牌”。在這種形勢下，導致學校把教育的重心放在升學率上，狠抓學生成績，成績代表一切，忽略學生傘面發展。而我國一再強調的素質教育被拋之腦后，我們雖然不能否定素質教育在近些年的確取得了進步，但愈演愈烈的仍然是升學率。因此，我們基于ARIMA模型分析我國高中升學率現狀，并對升學率做出預測。

ARIMA模型在升學率分析預測中的應用

（1）文獻回顧

有關升學率方面的研究文獻并不多，而且已有文獻多數是在理論上討論如何提升綠色升學率以及升學率的影響因素等。有學者以初中畢業生為研究對象，分析了升學率現狀以及影響因素，研究表明，初中升學率逐年遞增，并且衡量了教育資源和經濟因素對升學率的影響，各種因素對升學率的影響表現出了性別差異。還有學者從社會教育分析追求升學率的原因，研究對象集中在中小學，研究表明，追求升學率是我國國情和現行教育體制及考試制度下的必然結果。還有部分作者對片面追求升學率的嚴重后果進行了探討，這一定程度上會導致學生體質下降、創造力泯滅、教育價值取向出錯等后果，應該重視素質教育。有作者從實證方面人手，對我國基礎教育經費投入與小學升學率的關系機制進行統計分析，但幾乎沒有文獻專門就高中升學率進行過研究。

（2） ARIMA模型

ARIMA模型又稱為白回歸積分滑動平均模型（Autoregressive IntegratedMoving Average Model，簡記ARIMA），是指將非平穩時間序列轉化為平穩時間序列，然后將因變量僅對它的滯后值以及隨機誤差項的現值和滯后值進行回歸所建立的模型。根據原序列是否平穩以及回歸中所含部分的不同，包括移動平均過程（MA）、自回歸過程（AR）、自回歸移動平均過程（ARMA）以及ARIMA過程。其中AR是自回歸，p為自回歸項；MA為移動平均，q為移動平均項數，d為差分次數。

設yt是d階單整序列，及yt～I（d），則：w_t=△_dy_t=（1-L）_dy_t，其中w_t為平穩序列，對其建立ARMA（p.q）模型：w_t=c+Φ₁w_t-1+…+Φ_pw_t-p+ε_t+θε_t-1+…+θ_qε_t-q，

用滯后算子表示為：Φ（L）w_t=c+Θ（L）ε_t。經過d階差分的ARMA（p，q）模型稱為ARIMA（p，d，q）模型。

模型的應用

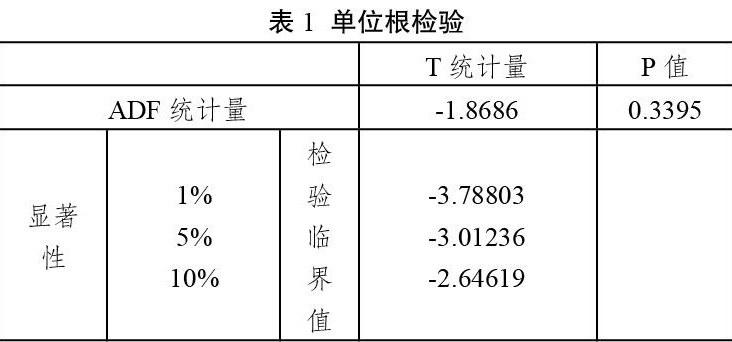
（1）序列平穩性檢驗

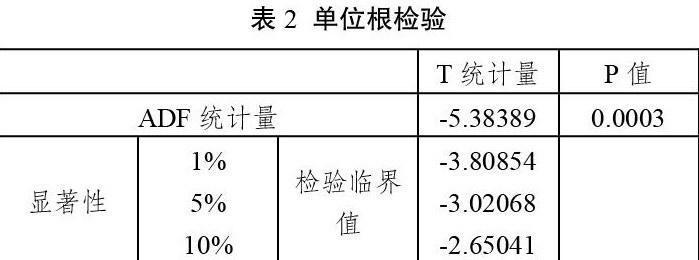
檢驗結果表明，ADF單位根檢驗值均大于臨界值1%、5%和10%，說明高中升學率在33.95%的顯著性水平下接受原假設，不能拒絕單位根的存在，因而時間序列是非平穩的。接下來，我們對序列進行差分，消除不平穩性。經過單位根檢驗，最終經過2階差分后，序列達到平穩性。模型的ADF檢驗結果如下：結果表明，升學率的二階差分序列在0.03%的顯著性水平下拒絕原假設，單位根不存在，序列是平穩的。

（2）模型定階及建立

序列經過兩次差分后，成為平穩序列，因此可以確定d為2。再利用二階差分后序列的白相關函數和偏自相關函數圖像或者AC和PAC值，初步確定AR和MA的階數，如圖所示：

根據AC和PAC的拖尾和截尾性質判斷。AR過程具有AC截尾、PAC拖尾的特征，而MA過程具有AC拖尾、PAC截尾的特征，從圖中可以看出AC和PAC都具有拖尾性質，因此我們設置ARIMA模型，但具體模型的設定還需要嘗試，并沒有沒有一個統一的準則。

通過二階差分后的升學率的相關圖和偏白相關圖可以看出，在1階后，自相關系數開始逐漸趨于0，但是在5，7，8，9階系數顯著不為零。偏自相關系數在1階后逐漸減小，但在5，6，8階處顯著不為零，因此為了設置更加合理的模型，我們可以選擇將不顯著的階數剔除。經過不斷嘗試，保證AIC和SC值最小的前提下，最終確定ARIMA（（5，6，8），2，（7））模型作為最終預測升學率的最優模型。

（3）模型參數估計及檢驗

通過Eviews軟件對模型ARIMA（（5，6，8），2，（7））進行估計，模型的估計結果顯示，在5%的顯著性水平下，ma（7），ar （5），ar （6），ar （8）的系數均顯著，系數分別為：-0.98，-0.9，-0.67，-0.26。sc值為3.84，AIC值為3.62。樣本的擬合優度達到了94.1%，說明二階差分后的升學率的絕大部分信息都可以南ARIMA（（5，6，8），2，（7））模型予以解釋。由模型的估計結果，可以確定模型的具體形式：

接下來對建立的模型進行檢驗，主要是檢驗殘差序列是否為白噪聲系列，檢驗自噪聲序列的方法有多種。我們可以檢驗序列均值是否為零。檢驗結果顯示P=1，接受原假設，即期望值為0，說明殘差是一個白噪聲序列。我們還可以檢驗序列的純隨機性，通過殘差序列的Q量對應的P>0.05值可以判斷，序列為白噪聲序列。以上結果可以說明模型通過檢驗。

模型的預測

利用我國升學率前幾年的數據建立模型，分析高中升學率的變動趨勢。模型預測前，我們需要先對模型進行檢驗分析，以便了解模型是否合適，即證明所建立的模型與數據真實值相符。

（1）模型擬合效果

首先，我們用建立的ARIMA（（5，6，8），2，（7》模型來對2000年-2012年度數據進行預測，比較真實值與擬合值之間的殘差，由圖表可以看出，隨著預測是時間的增加，升學率真實值與擬合值之間的差值越來越小，絕對誤差逐漸趨于0，擬合精度提高。然后我們繼續用2013年度數據對這個模型的擬合精度進行驗證。2013年度升學率真實值為87.6%，預測值為89.5%，相對誤差為2 .1010，說明模型的擬合預測效果較好，可以作為預測2014年升學率，結果的可信度較高。

（2）模型預測結果。

針對我國教育部門提供的高中升學率數據，目前最新數據為2013年數據。我們通過ARIMA模型，我們對2014年數據進行預測。預測結果顯示2014年升學率為84.5%，相比2013年來講，升學率下降。

結論

（1）文章結果表明我國高中升學率在1990年-2007年是一個先增加后下降的趨勢，2008年-2013年呈現上升趨勢。但總的來說，1990年-2012年間，我國升學率增加了59.7%。在這期間，升學率達到兩次頂峰，分別是在1990年-1998年、1999年-2007年期間的1996年（51%）和2002年（83.5%），這從側面反映了我國對教育事業的重視，增加教育投入，師資隊伍都可以提升文化軟實力，這也為是其他領域發展的奠定了文化基礎。

（2）升學率這一不斷增加的趨勢，也反映了我國過于追求學生成績的一個不良現象，我們應該注重提升綠色升學率，注重培養學生創新精神和實踐能力，提高學生自身素養和能力是提高綠色升學率的根本。同時，老師注重德育方法，培養高尚品德的學生。

[1]田立勇，杜憲素，王素娟.我國基礎教育經費投入對小學升學率影響的實證研究[J].長春教育學院學報，2014， 30（09）：113-114+125.

[2]孫志軍.我國初中升學率的基本狀況及影響因素研究[J].教育與經濟，2012（03）：9-13.

[3]吳明禮.片面追求升學率之我見[J].蘭州教育學院學報，2010，26（ 01）：145-146+159.

[4]張寶昆，黎春進.中國學校追求升學率的理論思考[J].云南師范大學學報（哲學社會科學版），1997（02）：4-10.

[5]熊志斌.ARIMA融合神經網絡的人民幣匯率預測模型研究[J].數量經濟技術經濟研究，2011，28（ 06）：64-76.

[6]張越，王勝難，劉媛，王偉炳.應用ARIMA模型對呼吸系統疾病月住院量及住院費用的預測[J].中國衛生統計，2015，32（02）：197-200.

[7]張勃，劉秀麗.基于ARIMA模型的生態足跡動態模擬和預測一一以甘肅省為例[J].生態學報，2011，31（20）：6251-6260.