河北省居民消費水平指數預測研究

高雅碩

居民消費水平指數反映居民的實際消費水平，影響著經濟的發展。為了預測未來河北省居民消費水平的變化趨勢，本文采用經濟預測研究中較少采用的方法，即逐步自回歸模型和狀態空間模型。比較兩個模型的預測結果，從中選出最優的模型進行預測。結果發現，與狀態空間模型相比，逐步自回歸模型的樣本內誤差較大，但樣本外誤差較小，即預測效果較好。因此選用逐步自回歸模型進行預測。發現未來河北省居民消費水平指數仍繼續增長，但增長速度下降，保持在4%-5%之間。

居民消費水平指數

逐步自回歸模型 狀態空間模型

居民消費水平是指居民為了滿足生存及生活需要而購買產品和勞務的人均消費支出，反映了人民的生活質量水平和消費需求。隨著經濟增長和社會進步的提高，居民消費水平也在發生著變化，進而影響著經濟的發展。居民消費水平指數可以反映居民實際的消費水平及變化趨勢。因此，預測居民消費水平指數（Household consumption expenditureindex， HCEI），不僅了解居民的消費需求和消費規律，還為政府制定政策提供依據，促進地區的經濟協調發展。目前，居民消費預測常采用時間序列預測（劉川和牛忠江（2010）；肖良（2016）；）和灰色預測方法（雷雨（2014）；王璐等（2016））。為了解河北省居民消費水平的未來發展趨勢，本文采用研究中較少使用的預測方法，建立逐步自回歸模型和狀態空間模型，從中選出最優的模型進行預測。

模型、方法和數據

（1）模型的介紹

逐步自回歸模型是將時間趨勢回歸模型和自回歸模型結合在一起，并用逐步篩選方法來選擇用于自回歸過程的滯后階數。模型如下：

Y_t=b₀+b₁t+b₂t₂+u_t

（1）u_t=a₁u_t-1+a₂u_t-2+…+a_pu_t-p+ε_t，其中t表示時間，Y_t表示觀測變量，ε_t是獨立的，均值為零的隨機誤差。

狀態空間模型是通過狀態向量表示多元時間序列的模型。狀態向量包含了即可觀測又不能直接觀測到的所有信息，真正反映了系統具有的狀態。狀態空間模型建立了觀測變量和狀態變量之間的關系，設X_t，ξ_t為2個多元時間序列，滿足 X_t=G_tξ_t+W_t=1，2，…. （2）ξ_t+1=F_tξ_t+V_t，t=1，2，….（3）其中，V_t，W_t是正交時間序列，F_t，G_t為系數矩陣。通常稱ξ_t為狀態向量，X_t為觀

測向量。式（2）稱為量測方程，式（3）稱為狀態轉移方程。式（2）和式（3）稱為狀態空間模型，該模型可以同時預測多個時間序列。

（2）數據和方法

本文數據來源于2016年河北經濟年鑒，除了2016年數據來源于河北省國民經濟與社會發展統計公報和河北省統計局的相關文章。為選出最優模型，定義1978-2013年為訓練集，2014-2016年為測試集。最后，在1978-2016年的數據上建立最優模型并預測。本文模型的評價指標為平均相對誤差，即相對誤差序列的期望。其中相對誤差是指預測值與實際值的偏差占實際值的百分比。

模型的篩選

（1）逐步自回歸模型

對訓練數據建立逐步自回歸模型并作三步預測，對TREND=1，2，3作試算分析。發現Trend=3時，模型的預測效果較好。因此取TREND=3建立逐步同歸模型，結果如下：{HCEI_t=290.89-39.16t+2.35t₂+u_t（4）u_t=0.81u_t-1+ε_t

式（4）中可以看出，模型建立了居民消費水平指數關于時間t的二次多項式模型，其殘差服從AR （1）模型。

（2）狀態空間模型

狀態空間模型要求時間序列是平穩的，因此檢驗并計算發現經過差分的對數序列是平穩的（表1）。表中F為與漂移項、單位根項和趨勢項有關的聯合檢驗統計量。可見HCEI對數序列的二次差分序列是平穩的，GDP指數對數序列的一次差分序列是平穩的。

對轉換后的平穩序列建立模型，得出最終的狀態轉移方程為：

（0.467090-0.07927977 ξ_t=

ξ_t+ε_t+1（5）

0.449843 0.494129）

（3）模型結果比較

計算各模型的平均相對誤差，結果如表2。表中可知與狀態空間模型相比，逐步自回歸模型的樣本內誤差較大，但各年的預測值與實際值相差較小，從而樣本外誤差較小。這說明了樣本內誤差和樣本外誤差并不是正相關。綜上選定逐步自回歸模型為最優模型。

河北省居民消費水平指數預測

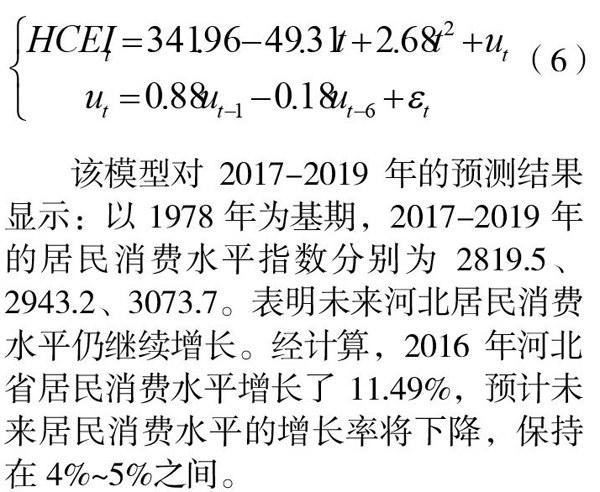
對1978-2016年的居民消費水平指數重新建立逐步自回歸模型，并預測2017-2019年的數據。最終建立的模型為居民消費水平指數關于時問t的二次多項式模型，其擾動項服從AR （6）模型。具體如下：HCEIsub>t