黏彈性地基上歐拉梁的橫向自由振動

彭麗 王英

Free transverse vibration of Euler-Bernoulli

beams resting on viscoelastic foundation

Peng Li， Wang Ying

（College of Civil Engineering，Shanghai Normal University，Shanghai 201418，China）

Abstract：

This paper focuses on the free transverse vibration of an Euler-Bernoulli beam resting on three-parameter viscoelastic foundation.Under simply supported boundary conditions，the exact frequency equations and the modal functions are given，and the explicit formulae for natural frequencies and modal functions are derived.Therefore we provide a simple and convenient way to obtain analytical solution of any order natural frequencies and modal functions.In numerical examples，with the explicit formulae，the low and high order natural frequencies are calculated easily，avoiding calculation error from numerical methods.The effects of the different parameters of the Euler-Bernoulli beam and the viscoelastic foundation on the free vibration characteristics are also numerically demonstrated.

Key words：

Euler-Bernoulli beams; viscoelastic foundation; natural frequency; mode

CLC number： O 32Document code： AArticle ID： 1000-5137（2018）01-0031-06

摘要：

研究了黏彈性三參數地基上有限長歐拉梁的橫向自由振動.給出了簡支邊界條件下的頻率方程和模態方程，進而推導出模型地基梁的固有頻率和模態函數的解析表達式，提供了精確計算任意一階頻率和模態的簡便方法.在具體算例中，運用推導出的公式能方便地計算出低階和高階頻率的精確值，避免了以往數值方法帶來的計算誤差.同時通過具體算例分析了不同物理參數對黏彈性地基上歐拉梁的振動特性的影響.

關鍵詞：

歐拉梁; 黏彈性地基; 固有頻率; 模態

Received date： 2018-01-05

Biography： Peng Li（1973-），female，doctor，associate professor，research area：Engineering mechanics.E-mail：pengl@shnu.edu.cn

引用格式： 彭麗，王英.黏彈性地基上歐拉梁的橫向自由振動 [J].上海師范大學學報（自然科學版），2018，47（1）：31-36.

Citation format： Peng L，Wang Y.Free transverse vibration of Euler-Bernoulli beams resting on viscoelastic foundation [J].Journal of Shanghai Normal University（Natural Sciences），2018，47（1）：31-36.

1Introduction

Finite beams resting on foundations are widely used in engineering structures，such as roads，bridges，airport pavements or railway engineering equipment.Because of its great practical importance，vibration analysis of the foundation beams are of great interest in the area of transportation and civil engineering [1-2].In most of the published researches on the topic，the problem are mainly studied by approximate methods such as finite element method [3-4]，transfer matrix method [5]，Rayleigh-Ritz method [6]，differential quadrature methods [7-8]，and Laplace transform technique [9].These studies are about elastic foundation，without accounting for any damping factor in foundation.In fact，the damping factors have very important effects on vibration of elastic beams on foundation.In recent years，researchers began to study free vibration of elastic Euler-Bernoulli beams resting on viscoelastic foundation [10-12]，but the published works on this specific problem are studied by different numerical method with approximate solutions.

For most elastic Euler-Bernoulli beams resting on viscoelastic foundation，the values of low order natural frequencies are small and the difference of adjacent order values is tiny，so slight error inevitably creeps into the calculations by numerical method，often with missing error.Furthermore，as order growing，error often increases greatly.Therefore，it is very difficult to obtain the credible values of higher order natural frequencies.To overcome these adverse effects，the present paper develops an exact method to study the free transverse vibration of Euler-Bernoulli beams on viscoelastic Pasternak foundation.The explicit formulae for natural frequencies and corresponding modal functions of beams on three-parameter foundation are derived，and provides a simple and convenient way to obtain analytical solution of any order natural frequencies and modal functions.

2Governing equations

Figure 1The model of an Euler-Bernoulli beam on

viscoelastic Pasternak foundation

A finite elastic Euler-Bernoulli beam element of length L mounted on three-parameter viscoelastic Pasternak foundation （figure 1）.Denote the beam mass density as ρ，area of cross-section as A，cross-sectional moment of inertia as I.

The governing differential equation of free motion for the beam on the viscoelastic Pasternak foundation can be written as [11]

ρA2w（x，t）t2+EI4w（x，t）x4+k1w（x，t）-k22w（x，t）x2+μw（x，t）t=0，（1）

where k1，k2 and μ are foundation normal stiffness，the shear parameter and damping coefficients，respectively.w（x，t） is the transverse deflection of the beam at the neutral axis coordinate x and time t.

After Introducing the dimensionless coordinates or parameters[11]，equation （1） can be transformed into the dimensionless equation

w，tt+k2fw，xxxx+k1w-k2w，xx+μw，t=0.（2）

where kf is dimensionless beam stiffness.

3Natural frequency and modal function

The vibration solution to equation （2） can be assumed as

w（x，t）=∑∞n=1ψn（x）eλnt，（3）

where λn=-δn+iωn，（n=1，2，3，…），δn is the nth decrement coefficient， ωn is the nth natural frequency，and ψn（x） are the nth mode functions of the transverse displacement.

Substitution of equation （3） into equation （2） yields

ψ（4）n（x）+λ2n+μλn+k1k2fψn（x）-k2k2fψ″n（x）=0.（4）

The 4th order homogenous constant-coefficient ordinary differential equation has the general solutions

ψn（x）=Cn1eiγn1x+Cn2eiγn2x+Cn3eiγn3x+Cn4eiγn4x，

（5）

where Cn1，Cn2，Cn3，Cn4 are constants to be determined.

Substitution of equation （5） into equation （4） yields the characteristic equation

γ4n+k2k2fγ2n+λ2n+μλn+k1k2f=0.（6）

Equation （6） has 4 roots：

γn1，n2=±-k22k2f-k22-4k2f（k1+μλn+λ2n）2k2f

γn3，n4=±-k22k2f+k22-4k2f（k1+μλn+λ2n）2k2f

.（7）

Consider the dimensionless pinned-pinned boundary conditions

ψn（0）=ψn（1）=0，ψ″n（0）=ψ″n（1）=0.（8）

Substitution ofequation （5） into equation （8） yields

1111

-γ2n1-γ2n1-γ2n3-γ2n3

eiγn1e-iγn1eiγn3e-iγn3

-γ2n1eiγn1-γ2n1e-iγn1-γ2n3eiγn3-γ2n3e-iγn3

Cn1

Cn2

Cn3

Cn4=0

0

0

0.（9）

The nonzero solution condition of equation （9） can be written as

-e-i（γn1+γn3）（-1+e2iγn1）（-1+e2iγn3）（γ2n1-γ2n3）2=0，（10）

with the unique solution satisfied by

γn3=nπ.（11）

Substitution of equation （7） into equation （11） yields

-k22k2f+k22-4k2f（k1+μλn+λ2n）2k2f=nπ.（12）

Solving equation （2），the explicit formulae for natural frequency λn，decrement coefficients δn and fundamental natural frequencies ωn are obtained as

λn=-μ2+in4π4k2f+n2π2k2+k1-μ4，（13）

δn=μ2， （n=1，2，…），（14）

ωn=n4π4k2f+n2π2k2+k1-μ4，（n=1，2，…），（15）

where δn and ωn are the real and imaginary parts of λn.

From equation （14），we noted decrement coefficients δn of an Euler-Bernoulli beam on viscoelastic Pasternak foundation is just equal to the half values of viscous damping coefficients μ，and it doesn′t change with the increase of order n.It is obviously different from the Timoshenko beam on same foundation [2].From equation （15），it can be easily found that with the increasing of beam stiffness kf，mean stiffness of foundation k1 and shear parameters of the foundation k2，the natural frequencies ωn increase.But with the increase of viscous damping coefficients μ，the natural frequencies ωn decrease.Moreover，the beam stiffness has the most important effect on the the natural frequencies.

Furthermore，based on equation （9），one can get

C2n=-C1n，C3n=-e-iγn1+iγn3（-1+e2iγn1）-1+e2iγn3C1n，C4n=e-iγn1+iγn3（-1+e2iγn1）-1+e2iγn3C1n.（16）

And from equation （5），the nth modal function of transverse vibration is rewritten as

ψn（x）=C1neiγn1x-e-iγn1x-ei（γn3x+γn3-γn1）（-1+e2iγn1）-1+e2iγn3+ei（-γn3x+γn3-γn1）（-1+e2iγn1）-1+e2iγn3.（17）

With explicit formulae fornatural frequency λn，the explicit formulae for modal function can also be easily obtained.For computing the modal functions，the normalization condition is used to determine constant C1n.

4Numerical results

Consider a finite elastic Euler-Bernoulli beam resting on three-parameter viscoelastic foundation，the parameters of the beam and foundation come from the model beam [12].From equation （15），with explicit formulae，the accurate values of any order natural frequency can be easily and exactly calculated.The first eight and the high order dimensionless values are listed in Table 1 and Table 2.In former research works，it was nearly impossible to obtain accurate high order frequencies by numerical method.

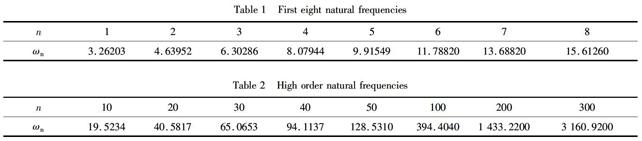
From explicit formulae formodal function of equation （17），the first four modal functions are obtained and shown in figure 2.The real and imaginary parts are symmetric about x axial.With the increase of orders，the amplitudes of the modal functions decrease a little.

Table 1First eight natural frequencies

Table 2High order natural frequencies

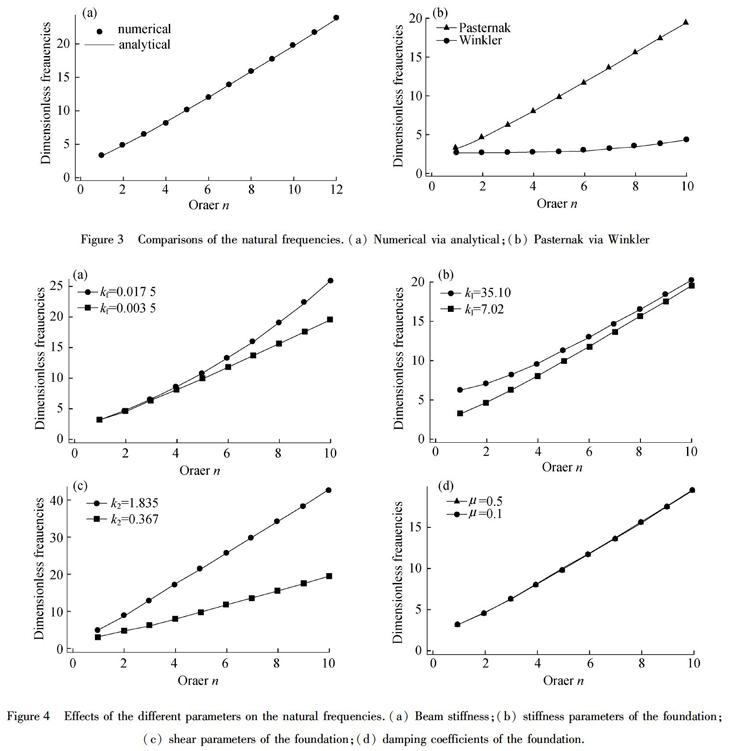
For the same model foundation beam，the values ofnatural frequency were found by different numerical method[12].Figure 3（a） compares the analytical solutions of natural frequencies with the numerical data.Under simply supported boundary conditions，the two results fit very well.Figure 3（b） shows that the natural frequencies of a finite elastic Euler-Bernoulli beam on viscoelastic Pasternak foundation are larger than that of the same beam on viscoelastic Winkler foundation，and with the increase of orders，the natural frequencies of the beam on viscoelastic Pasternak foundation increase more quickly.

Figure 2First four modal functions.（a） Real parts;（b） imaginary parts

Figure 3Comparisons of the natural frequencies.（a） Numerical via analytical;（b） Pasternak via Winkler

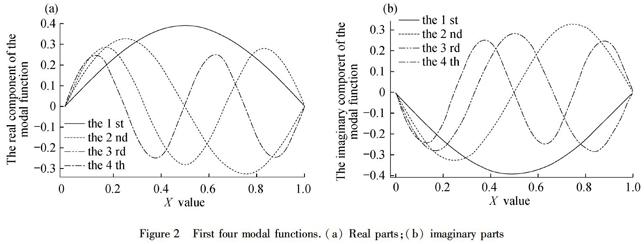
Figure 4Effects of the different parameters on the natural frequencies.（a） Beam stiffness;（b） stiffness parameters of the foundation;

（c） shear parameters of the foundation;（d） damping coefficients of the foundation.

For the modal beam resting on three-parameter viscoelastic foundation，it shows beam and foundation parameters have different effects on the natural frequencies in figure 4.With the beam stiffness and the shear parameter of foundation increasing，the natural frequencies increase，and with the increase of orders，the difference of the high orders is larger than that of low orders.With foundation stiffness parameter increasing，the natural frequencies also increase，but the difference of the high orders is smaller than that of low orders.It also shows shear parameter of the foundation has the most effects on the natural frequencies.For different shear parameters，the natural frequencies of the first order are very similar，but with the orders increasing，the natural frequencies of the greater foundation shear parameters grow more quickly.

The viscous damping coefficient of the modal foundation beam is very small，with the increase of the viscous damping coefficients，the natural frequencies decrease so little that the difference isn′t obvious in figure 4.

5Conclusions

The free transverse vibration of Euler-Bernoulli beams on three-parameter viscoelastic foundation is investigated in this work.Under simply supported boundary conditions，the explicit formulae for natural frequencies and corresponding modal functions of the free transverse vibration are developed，avoiding calculation error from numerical ways.A simple and convenient method is provided to obtain analytical solutions of natural frequencies and modal functions of an Euler-Bernoulli beam on viscoelastic foundation.

The examples reveal that，with low order growing，the natural frequencies slightly increase，and the decrement coefficients have no change.Under simply supported boundary conditions，the analytical results have a good agreement with the numerical data.It shows that the natural frequencies of Pasternak foundation beam are larger than that of Winkler foundation beam.

From the explicit formulae for natural frequencies，it can be easily found that with the increase of beam stiffness，mean stiffness of foundation and shear parameters of the foundation，the natural frequencies increase.But as the viscous damping coefficients increasing，the natural frequencies decrease.Moreover，the beam stiffness has the most important effects on the natural frequencies.

References：

[1]Kargarnovin M H，Youneslan D，Thompson D J，et al.Response of beams on nonlinear viscoelastic foundations to harmonic moving loads [J].Computers & Structures，2005，83：1865-1877.

[2]Peng L，Ding H，Chen L Q.Frequencies，modes and orthogonality of vibrating timoshenko beams on viscoelastic foundation [J].Journal of Vibration Engineering & Technologies，2016，4（6）：527-537.

[3]Franciosi C，Masi A.Free vibration of foundation beams on two parameter elastic soil [J].Computers and Structures，1993，47：419-426.

[4]Rossi R E，Laura P A A.Numerical experiments on vibrating linearly tapered Timoshenko beam [J].Journal of Sound and Vibration，1993，168：179-183.

[5]Yokoyama T.Vibration analysis of Timoshenko beam-Columns on two-parameter elastic foundations [J].Computers & Structures，1996，61（6）：95-1007.

[6]Irie T，Yamada G，Takahashi I.Vibration and stability of a non-uniform Timoshenko beam subjected to a flower force [J].Journal of Sound and Vibration，1980，70：503-512.

[7]Chen C N，Vibration of prismatic beam on an elastic foundation by the differential quadrature element method [J].Computers & Structures，2000，77：1-9.

[8]Gutierrez R H，Laura P A A，Rossi R E.Fundamental frequency of vibration of a Timoshenko beam of non-uniform thickness [J].Journal of Sound and Vibration，1991，145：241-245.

[9]Magrab E B.Natural frequencies and mode shapes of Timoshenko beams with attachments [J].Journal of Vibration and Control，2007，13（7）：905-934.

[10]Peng L，Chen C X.Analysis of vibrations of beams on viscoelastic winkler foundations [J].Journal of Shanghai Normal University （Natural Sciences），2012，41（6）：586-589.

[11]Peng L，Ding H，Chen L Q.Complex modal analysis of vibrations of beams on viscoelastic pasternak foundations [J].Journal of Vibration and Shock，2013，32：143-146.

[12]Peng L，Wang Y.Differential quadrature method for vibration analysis of beams on viscoelastic foundations [J].Journal of Shanghai Normal University （Natural Sciences），2015，44（2）：132-137.