例談函數思想在數學教學中的滲透

江蘇濱海縣永寧路實驗學校(224500)

函數是研究變量和變量之間關系的數學模型。函數思想是指運用函數的概念與性質，分析問題、解決問題的一種思想策略。在小學數學學習階段，雖然函數的概念在教材中沒有正式提出，但函數關系在數學解決問題中并不少見。因此，教師應注重函數思想在數學教學中的滲透，使學生的數學學習變得更加簡單輕松，發展學生的數學素養。

一、在數學運算教學中滲透

數學運算是一種復雜的智力活動，在教學數學運算過程中，如果教師僅僅把教學目標局限于確定具體的數之間的關系，那么學生的思維則永遠停留在算術思維的層面上，很難感受到數學運算的結構化、抽象化等特征。因此，教師應注重函數思想在運算教學中的滲透，使學生能夠對變化的數有聯系地進行思考，促進學生數學思維的發展。

例如，在加法教學中，教師出示情景圖(略)后問學生：“仔細觀察小兔采蘑菇的圖，你有什么發現？”有的學生說：“我發現小兔每次只采一個蘑菇。”有的學生說：“我發現小兔采的蘑菇越來越多。”于是，教師追問：“如果小兔一直這樣采蘑菇，怎樣才能求出小兔一共采了多少個蘑菇呢？你發現了什么規律？”在教師的啟發下，學生發現小兔每次采蘑菇的數量是不變的，而籃子里的蘑菇個數和總數則一直發生變化。在學生回答后，教師又鼓勵學生具體地說一說，使學生發現“蘑菇總數總比籃子里蘑菇的數量多1”的規律。這個規律的發現過程，其實是函數思想在教學中滲透的過程，有效提升了學生思維的高度。上述教學，學生在教師的啟發、引領下逐步發現“一個加數變化，引起和的變化”，從而使兩個變量之間的結構關系清晰地展現在學生面前，根據這種變量之間的關系，學生很容易推算出另一個變量的值。這樣教學，有助于學生用聯系發展的眼光看待對應量之間的關系，使函數思想在教學中得到有效滲透。

二、在數學公式教學中滲透

在學習周長、面積、體積等內容的過程中，需要運用大量的數學公式進行計算，所以教師可對學生進行函數思想的滲透，使學生的數學學習品質得到提升。

例如，教學“圓的面積”一課時，由于學生已經學習了正方形面積的計算，如果把正方形的面積計算公式作為一個函數模型的話，那么圓的面積就可以看作是正方形這個模型的推廣。假如把r平方看成是以r為半徑的正方形面積的話，那么圓的面積則是正方形面積的π倍。因此，教師教學時可從以半徑為邊長的正方形入手，通過數方格的辦法引領學生推導圓的面積計算公式，在這個推導過程中，學生可以把圓的面積與半徑平方的關系輕易地聯系起來。這樣不僅有助于學生猜想能力的發展，而且可以使學生自然地把圓的半徑r作為一個函數自變量的值，順利地求出對應的因變量(圓的面積)的值。上述教學，教師以圓的面積計算公式的推導為例，對學生進行函數思想的滲透，充分體現了函數思想在數學公式運用方面的價值，使學生在數學公式的學習過程中能夠舉一反三，并且學會用變化的眼光看待問題，對函數模型有了初步的認識與體會。

三、在數學規律教學中滲透

在數學教學中，許多數學問題往往隱含著一定的數學規律，教師如能根據教學需要，及時對學生進行函數思想的滲透，則可以幫助學生建立初步的函數模型，使學生探究數學規律的過程更加簡單、輕松。

例如，教學“找規律”一課時，有以下一道習題。

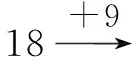
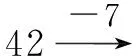
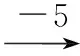
在這個找規律填數的教學中，教師先引導學生思考：“仔細觀察每個算式，想一想在每個算式中，每次是增加幾或者減少幾？”在學生觀察的基礎上，教師追問：“每次增加或者減少的數變了嗎？”“在這個算式中，哪些量發生了變化，哪些量沒有變化？你能把它們的規律找出來嗎？”“以‘18+9+9…’為例，如果這個算式繼續寫下去的話，那第11個空格應該填幾？第20個空格呢？”……通過問題，既使學生掌握了第幾個數就是增加了幾個9的規律，又讓學生對變量與不變量有了更加深刻的認識，這就使函數思想在教學中得到有效滲透，獲得顯著的教學效果。上述教學，教師以找規律為例，鼓勵學生主動探索規律、發現規律、運用規律，不僅激發了學生的探究興趣，而且使學生真正掌握了所學的知識。

總之，函數思想作為數學中的一種重要的思想方法，教師可結合數學運算、數學公式、數學規律等內容的教學，對學生進行函數思想的滲透，提高學生解決問題的能力，使學生的數學素養得到有效發展。