“輕繩滑輪模型”的一個重要結論

李偉康 包 容 陶亞飛

(蕪湖市第一中學，安徽 蕪湖 241000)

1 規律及推證

題目.如圖1所示, 長度為L的細繩的兩端分別系在豎立于地面上相距為d的兩桿頂端A、B,繩上放一個光滑的輕質滑輪,其下連著一重為G的物體,平衡時,繩中的張力為多大?

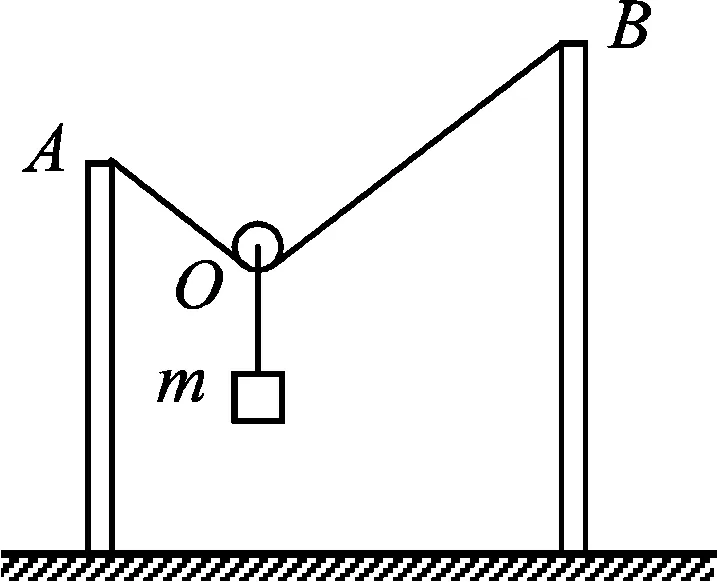
圖1

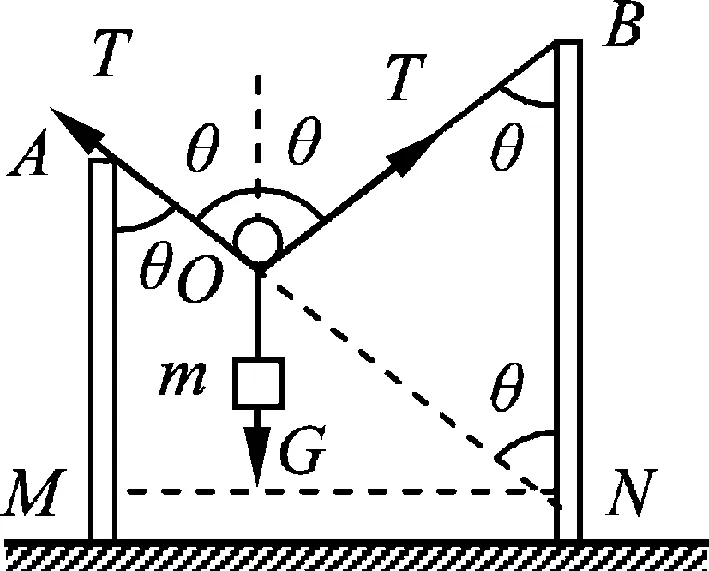
圖2

解析： 以滑輪和繩子接觸點為受力分析對象,由對稱性可知,兩邊張力大小相等,方向與豎直方向夾角也相等,設為θ(如圖2所示).延長繩AO,交右側直桿于N點,過N點做水平線,交左側直桿于M點,在△AMN中,

(1)

又受力分析知,

2Tcosθ=FN.

(2)

FN=G.

(3)

兩式聯立可解.

此類問題,均選繩子的“活結”為研究對象,其一般均是受3個力,即兩個拉力和一個壓力FN,只要理清以上3種關系即可順利求解.

2 常規應用(FN方向保持不變)

此種情況,只需要分析繩子兩端點間的水平間距變化情況即可根據(1)～(3)3式得出相應物理量的大小變化情況.

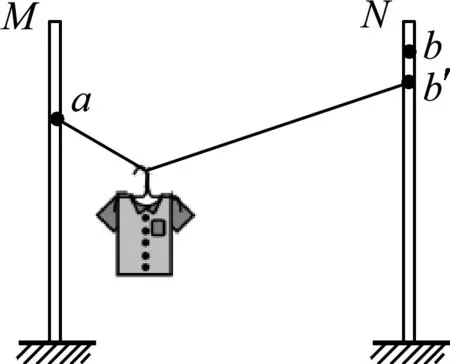
圖3

例1.(2017年天津卷)如圖3所示,輕質不可伸長的晾衣繩兩端分別固定在豎直桿M、N上的a、b兩點,懸掛衣服的衣架掛鉤是光滑的,掛于繩上處于靜止狀態.如果只人為改變一個條件,當衣架靜止時,下列說法正確的是

(A) 繩的右端上移到b′,繩子拉力不變.

(B) 將桿N向右移一些,繩子拉力變大.

(C) 繩的兩端高度差越小,繩子拉力越小.

(D) 若換質量更大的衣服,則衣架懸掛點右移.

解析： 繩的右端上移到b′,引起繩的兩端高度差變化,但繩子兩端點間的水平間距沒有變化,所以繩子拉力大小不變,(A)項正確,(C)項錯誤;將桿N向右移一些,繩子兩端點間的水平間距變大,由(1)、(2)兩式知,繩子拉力變大,(B)項正確;若換質量更大的衣服,由(1)式知,θ不變,再由(2)式知,繩子拉力變大,但根據“題目”推證過程知,θ不變,衣架懸掛點的位置就不變,(D)項錯誤.答案為(A)、(B).

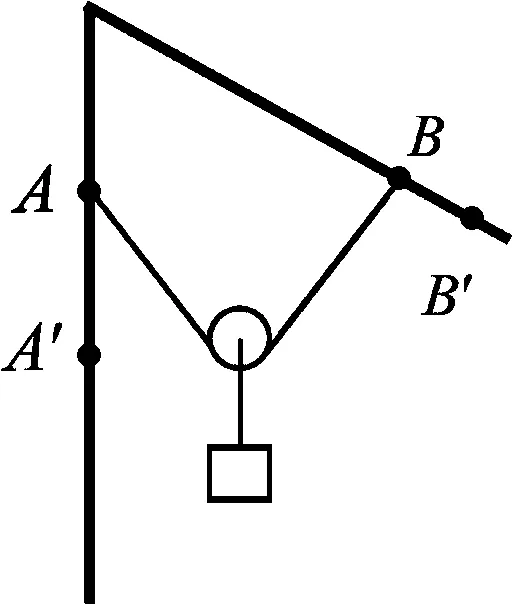
圖4

例2.如圖4所示,一根不可伸長的細繩兩端分別連接在框架上的A、B兩點,細繩繞過光滑的滑輪,重物懸掛于滑輪下,處于靜止狀態.若緩慢移動細繩的兩端,則繩中拉力大小變化的情況是

(A) 只將繩的左端移向A′點,拉力變小.

(B) 只將繩的左端移向A′點,拉力不變.

(C) 只將繩的右端移向B′點,拉力變小.

(D) 只將繩的右端移向B′點,拉力不變.

解析： 只將繩的左端移向A′點,繩子兩端點間的水平間距沒有變化,所以繩子拉力大小不變,(A)項錯誤,(B)項正確;只將繩的右端移向B′點,繩子兩端點間的水平間距變大,由(1)、(2)兩式知,繩子拉力變大,(C)、(D)兩項均錯誤.答案為(B).

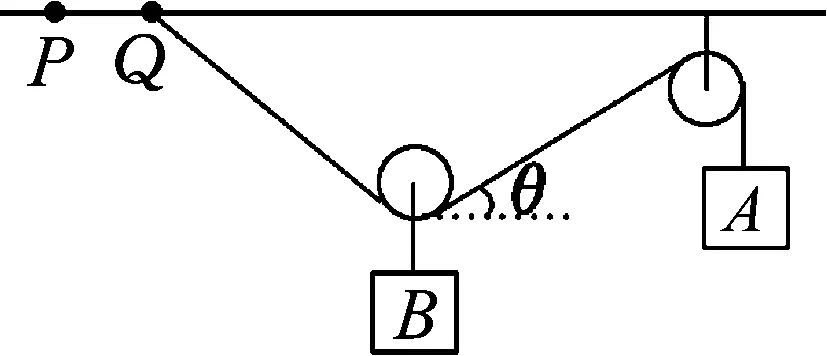
圖5

例3.如圖5所示,A、B兩物體的質量分別為mA和mB,且mA>mB,整個系統處于靜止狀態,小滑輪的質量和一切摩擦均不計.如果繩的一端由Q點緩慢地向左移到P點,整個系統重新平衡后,物體A的高度和兩滑輪間繩與水平方向的夾角θ如何變化

(A) 物體A的高度升高,θ角變大.

(B) 物體A的高度降低,θ角變小.

(C) 物體A的高度升高,θ角不變.

(D) 物體A的高度不變,θ角變小.

解析： 對A受力分析知,繩上張力不變,由(2)式知,θ不變.而繩的左端到定滑輪的水平距離變大,再由(1)式知,定滑輪左側繩子變長,所以右側繩子變短,物體A的高度升高.答案為(C).

3 “等效”應用(FN方向發生變化)

此類情況,(1)式中的“d”和(2)式中的“θ”均應采用等效含義：d為繩子兩端點沿垂直于FN方向的距離,θ為繩子張力與FN所在直線間的夾角.

3.1 FN大小保持不變

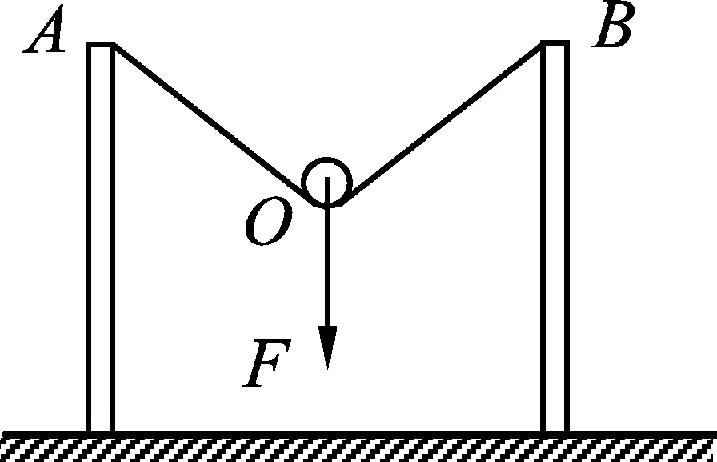
圖6

例4.如圖6所示,輕質繩子兩端分別固定在兩根等高的豎直桿上,對繩上一輕質動滑輪施加大小恒定的拉力F作用,不計各種摩擦.在拉力方向由豎直向下緩慢變到水平向右的過程中,繩上的張力大小如何變化

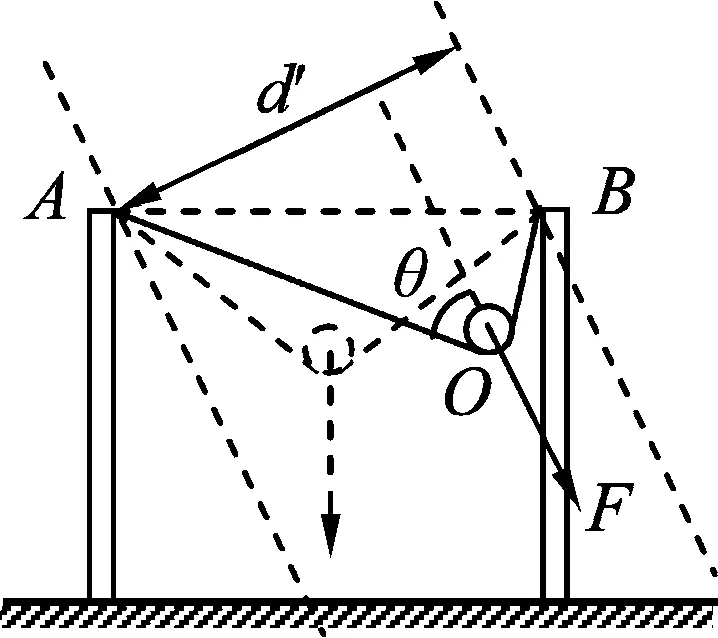
圖7

(A) 逐漸變大.

(B) 逐漸變小.

(C) 保持不變.

(D) 先變大后變小.

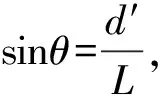
圖8

3.2 FN大小發生變化

例5.如圖8所示,晾曬衣服的繩子兩端分別固定在兩根等高的豎直桿上,繩子的質量及繩與衣架掛鉤間摩擦均忽略不計.原來衣服保持靜止,一陣恒定的風吹來,衣服受到水平向右的恒力而發生滑動,并在新的位置保持靜止.則相比原來,在新的位置時

(A) 掛鉤左右兩邊繩的拉力不再相等.

(B) 繩的拉力一定不變.

(C) 繩對掛鉤作用力變大.

(D) 繩對掛鉤作用力不變.

解析： 通過分析,易知(A)、(D)選項錯誤,(C)選項正確,作為單選題,答案為(C).通過極限法分析,可以知道(B)選項錯誤.

但有學生對極限法的信度提出了質疑,好奇心和求知欲驅使他們想知道繩的拉力大小變化情況.經過師生討論,現給出分析過程如下.

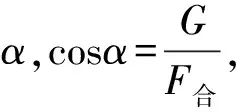
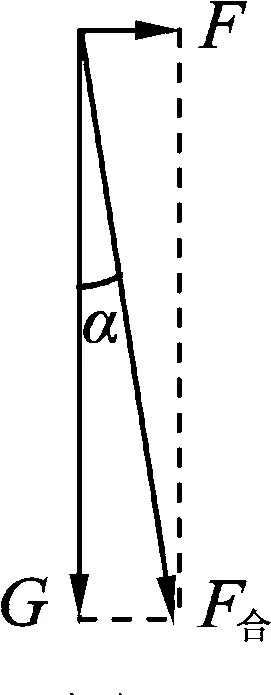
圖9

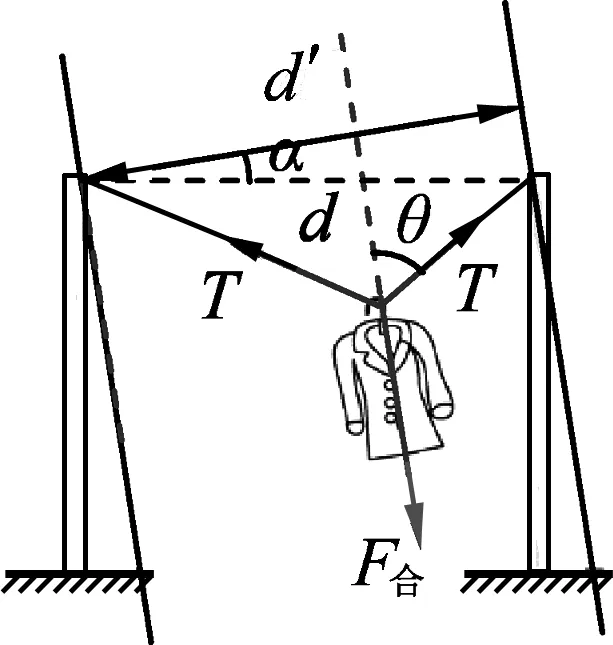
圖10

現做如下討論:

范圍內,繩子的張力T隨風力F的增加而增大.

綜上,例5中繩子的拉力應做如下變化(設無風時繩子的拉力大小為T0):

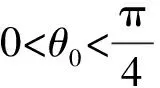
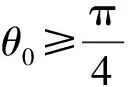
4 規律拓展

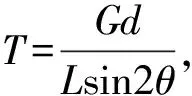
參考文獻：

1 周化海,黃紹書.彈力方向的正確理解與分析——從一道選擇題的剖析談起[J].物理教師,2017(8):89-90.