一種改進的螺旋齒銑刀立銑切削力計算方法

竇 煒，袁勝萬，何曉聰

(1.昆明理工大學 機電工程學院，昆明 650500；2.沈機集團昆明機床股份有限公司，昆明 650000)

銑削加工過程中，銑刀各齒周期性的切削工件產生大小和方向不斷變化的動態銑削力，引起刀具與工件的受迫振動。振動會使刀具在工件表面留下振紋，影響表面粗糙度，并且在一定不利條件下有可能使銑削力產生不穩定的振蕩，進而導致整個銑削系統失穩。為了獲得高質量的加工表面，需要將刀具相對工件的振動狀態控制在可以接受的范圍內。利用動力學模型研究銑削過程的動態特性和穩定性是銑削研究的重要手段。

當銑床主軸帶動刀具旋轉時，同一刀齒上位于刀具軸向不同位置的刀刃將先后切入或切出工件，其時間間隔或延遲取決于刀刃之間的軸向距離以及刀齒螺旋角。因此，在某一時刻，刀齒有可能只有部分刀刃參與切削，這將導致該刀齒上不同軸向位置的刀刃所受切削力各異，并且不同時刻作用于該刀齒的總切削力也可能不是常數。

針對立銑加工的上述特點，Altintas和Engin等[1-3]較早對不同類型的立銑刀(Helical end mill tool)銑削過程開展了系統性研究，給出了一種不同于經典的直齒銑刀模型的螺旋齒銑刀模型，該模型可以計算不同幾何特征的立銑刀銑削力，并進一步歸納總結了立銑加工過程中的 “刀具-工件” 動力學模型及分析的基本方法。Balachandran等[4-5]對不同徑向切深條件下的銑削加工過程的動力學問題進行了研究，分析了小徑向切深時銑刀與工件的斷續接觸對系統穩定性的影響。Merdol[6]在采用Budak等的方法分析小徑向切深時的銑削加工穩定性得到了相同的結果。但是他們的研究局限于小軸向切入深度，因此刀刃切入和切出“延遲”效應不明顯。Insperger等[7-8]對比分析了大軸向切入深度條件下的經典銑刀模型(直齒)和螺旋齒銑刀模型的穩定性表現，指出后者的穩定性葉瓣圖中存在封閉的不穩定“孤島”，并通過試驗證明了這一現象。

因此，小軸向切深立銑時若忽略刀刃切入和切出“延遲”效應，即認為銑削過程中參與切削的刀刃段恒等于刀具的軸向切入深度，螺旋齒銑削模型近似退化為直齒銑削模型，銑削分析的結果在一定程度上仍然能夠與實際加工情況相吻合。但是，針對諸如加工薄壁構件的大軸向切入深度的銑削研究，則必須考慮螺旋齒銑削時的切削力時變特點。并且，若忽略了刀刃切削部分是隨著刀具旋轉逐漸增加并逐漸減少的實際過程，銑削力中還將包含失真的高頻成分的影響，從而導致后續分析產生錯誤結果。

隨著學者們對銑削的研究不斷深入，提出的銑削力模型以及研究的問題越來越復雜[9-15]。然而，在銑削加工動力學分析或求解過程中，螺旋齒銑刀銑削力的計算仍普遍采用將刀具沿軸向離散成微元段逐個計算然后求和的近似方法，這是一個相對耗時的環節。本文推導得到螺旋齒銑刀切削力的一種解析表達式，簡化了銑削力的計算過程，從而提高銑削動力學方程的求解效率。

1 立銑加工動力學模型

雖然不同幾何特征的立銑刀局部切削力有所區別，但是銑削過程中刀具和工件之間的動力學關系是相同的。如圖1所示，銑削加工過程可以抽象為包含“動態切削力”和“刀具-工件系統”兩個相互作用的環節所形成的反饋系統。

圖1 銑削加工過程方框圖Fig.1 Block diagram of the milling process

下面以螺旋齒圓柱銑刀為例簡要概括立銑加工的動力學模型。圖2所示為二自由度立銑加工力學模型。在此假設工件為剛體，刀具相對工件為柔性體，且由于刀具軸向剛度通常遠遠高于橫切面剛度，因此只考慮銑削力作用于刀具X和Y方向的情況。設刀具有N個刀齒，記第j個刀齒所受切削力銑削力Fj，則根據牛頓定律，銑刀中心的位移向量q滿足下式：

圖2 二自由度“刀具-工件”系統力學模型Fig.2 Mechanical model of the 2DOF tool-workpiece system

(1)

其中

mx和my，cx和cy，kx和ky分別表示刀具在X方向和Y方向的模態質量，模態阻尼和模態剛度。切削力Fj包含由加工進給引起的“靜態力”(Static milling force)和再生效應(Regenerative effect)引起的動態力(Dynamic milling force)。x和y以及δx和δy則分別表示銑刀在銑削力作用下的“靜態位移”以及再生振動。

圖3 螺旋齒立銑刀及微元段Fig.3 Geometry of a helical tool and an infinitesimal element

以第j個刀齒為研究對象。如圖3所示，刀齒最前端Pj,1點Z軸坐標為0，取刀齒上距Pj,1點的軸向距離為z處的一個厚度等于dz微元段刀刃進行分析。刀具轉角以Y軸正向起始，順時針方向為正。記該處刀刃的瞬時角位移為φj(t,z)，其值可由如下函數關系求出：

(2)

式中：變量t表示時間，s。參數ω表示銑床主軸轉速，rad/s。β為銑刀螺旋角度，rad；r為刀具半徑,m。則該微元段刀齒受到的沿刀刃的切向和法向的銑削分力，ft和fn，可以用瞬時切屑面積和比切削力(Specific cutting force)的乘積表示為:

(3)

(4)

式(3)中，Kt和Kn分別表示刀刃切向和法向線性比切削力系數。h表示瞬時切屑厚度，其值約等于銑削過程中靜態和動態切屑厚度沿刀齒法向的投影，即：

(5)

式中:fz表示銑刀進給量。參數τ表示刀齒經過周期 (Tool passing period)。窗函數gj(t,z)的物理意義是：如果φj(t,z)介于刀齒切入角φs和切出角φe形成的區間內，則表示該處刀刃進入切削區參與切削，否則不產生切削力。

隨后將ft和fn投影至X-Y坐標系下，整理得到微元段刀刃受到的作用力dFj的表達式為：

(6)

其中矩陣Gj為：

于是，第j齒所受的總銑削力Fj等于所有微元段所受切削力的總和：

(7)

式(7)的積分上限為軸向切入深度b。將式(7)代入式(1)得：

(8)

式(8)即為描述螺旋齒銑刀立銑加工過程的時滯微分控制方程(Delay differential equations)。這類方程的一個主要特點是：方程所描述的動態系統的狀態向量q的變化率，同時取決于當前和過去的狀態向量值。

式(7)中的窗函數gj(t,z)給計算Fj帶來了困難。不論采用符號運算(Symbolic computation)或是數值積分(Quadrature)直接計算式(7)都非常繁瑣。因此，在實際運用中，很少通過積分的方法計算式(7)，而是采用離散求和近似的策略。具體而言，取足夠大的正整數n，將銑刀沿軸向切入深度b離散為n段，則第k段離散微元的角位移φj,k和所受切削力分別為：

(9)

(10)

于是，當n趨于無窮大時Fj等于：

(11)

取式(11)中的有限項求和(如n=100)替換式(8)中的積分，得到：

(12)

這種處理方法的優點在于：在每一個微元段內，窗函數gj化為常數，而計算式(10)只需初等函數的代數運算。隨后，式(11)的微元段連加運算可以非常容易地通過循環算法編程實現。缺點是如果切削力計算精度要求較高，則n值必須取的很大，而n值越大花費的計算時間就越多，因此這一步是限制銑削動力學方程求解效率的重要因素之一。

2 改進的銑削力計算方法

如果式(7)中的定積分被積函數不包含窗函數gj，銑削力計算將非常容易。式(2)表明，任意時刻刀刃微元的軸向位置z和該位置轉角存在一一對應的函數關系。因此可以通過變量代換，利用銑削過程中實際進入切削區的刀刃段的角位移作為積分域，從而將被積函數中的窗函數消去。

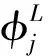
(13)

圖4 螺旋齒立銑刀逆銑加工Fig.4 Up milling with a helical end tool

式中：max和min分別代表最大值和最小值函數。φj表示第j齒前端Pj,1的瞬時角位移，其值由下式計算：

(14)

式中：mod為求余函數。式(13)中的參數φd稱為切削滯后角度，它表示第j齒前端Pj,1開始切削工件到刀齒切入末端Pj,2進入切削區域的這段時間內刀具所轉過的角位移，如圖4中的角∠P2,1OP2,2，其值由下式計算：

(15)

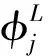
(16)

相應地，進入切削區的刀刃微元的厚度dz等于：

(17)

將式(16)和(17)中定義的φj,k和dz代入式(10)和(11)，對求和項取極限，得到Fj計算式如下：

(18)

經過式(18)的處理，式(7)被積函數中判斷刀齒是否進入切削區的窗函數gj被新的積分上下限取代了。式(18)的積分是變限積分，接下來需要確定積分限。

由φd的表達式(15)可知，若刀具半徑和螺旋角不變，切削滯后角度將是軸向切入深度b的函數，而銑削過程中的刀具切入角和切出角取決于徑向切入深度。因此，根據軸向和徑向切入深度的不同取值組合，該積分有以下兩種情況。當φs+φd<φe時:

(19)

當φs+φd≥φe時:

(20)

對式(19)和(20)進行積分并整理后，上述兩種情況的積分結果可統一表示為：

(21)

矩陣Aj(t)各元素的表達式分別為：

aj,xx(t)=-sin(φL-φU)sin(φU-φL)-

aj,xy(t)=-(φU-φL)-cos(φL+φU)×

aj,yx(t)=φU-φL-cos(φL+φU)×

aj,yy(t)=φU-φL-cos(φL+φU)×

(22)

(23)

將式(23)代入式(1)得：

(24)

3 求解立銑加工動力學方程

目前，只有少量表達式非常簡單的遲滯微分方程能給出解析解，形如式(12)或(24)的方程只能通過數值方法求解。銑削動力學方程的求解過程可以概括分解為如下步驟：

1) 選擇方程求解時間步長Δt，將時間變量t取值范圍離散為時刻ti序列(i=1,2,…)。如將刀齒經過周期τ離散為s段，則Δt=τ/s。

2) 計算ti時刻的切屑厚度h(ti)或H(ti,ti-s):

(25)

3) 計算銑刀所受的銑削力Fj(ti)。

4) 計算銑削力Fj(ti)作用下的銑刀位移q(ti)；

5) 將時刻ti值增加一個步長，并重復第2和第4步，直到最后一個離散時刻。

接下來通過仿真，對比利用解析表達式(23)和離散近似表示式(11)求解銑削動力學方程的效果。兩種求解方法均采用Matlab 9.0編程，除了切削力計算部分的代碼之外，兩種方法其余部分程序內容完全相同并且在同一臺電腦上運行(AMD A10-6800K4.4GHz，8GB RAM)。

仿真銑削模型參數來自文獻[8]：刀具X和Y方向模態參數相同，頻率319.38 Hz，阻尼比1.96%，剛度2.16×107N/m；刀具直徑20 mm，齒數為4，螺旋角30°；逆銑加工，徑向切深1 mm，進給量0.1 mm/齒，比切削力系數Kt= 804.3×106N/m2，Kn= 331×106N/m2。

圖5所示為軸向切深b=20 mm，主軸轉速Ω=10 000 r/min時刀具所受Y向切削力仿真結果，圖(b)為圖(a)的局部放大圖形，其中虛線和細實線分別表示采用式(23)和式(11)的結果。圖(a)中切削力最大幅值保持在95 N上下，表明模型處于穩定銑削狀態。圖(b)中的細實線"毛刺"顯示了采用式(11)求解方程的離散誤差。

圖5 Y向銑削力仿真結果(b=20 mm，Ω=10 000 r/min)Fig.5 Simulation results for Y direction force

如式(11)所示，隨著軸向微元段數目n趨于無窮大，該誤差將收斂為0。取時間步長Δt= τ/200，自變量范圍0～0.2 s，采用式(23)求解方程耗時0.672 4 s。以此結果作為基準，圖6顯示了采用式(11)求解方程時刀具離散微元段數目n對仿真結果的影響。

圖6中左邊y坐標軸表示相對誤差，右邊y坐標軸表示兩種方法求解消耗時間的比值。從圖中可以看出，采用離散近似的方法計算銑削力，耗時與n成正比。n=50的時候，相對誤差為6%，相對時間為2.1倍。當計算誤差小于0.5%，則n需大于500，耗時約為本文提出方法的18倍以上。

圖6 刀具離散微元段數對仿真的影響Fig.6 Effect of the number of elementary tool disks on simulation

圖7所示為軸向切深b=12 mm，主軸轉速Ω= 10 000 r/min時采用式(23)的仿真結果。圖(a)和圖(b)所示分別為Y向銑削力和位移。可以看出模型此時處于不穩定切削狀態。

圖7 不穩定銑削條件的仿真結果(b=12 mm，Ω=10 000 r/minFig.7 Simulation result of unstable milling

和圖5情況相比，主軸轉速不變，減小軸向切深，系統反而從穩定狀態變為不穩定。這是因為圖7的銑削條件處于螺旋齒銑刀的不穩定“島”內[8]，如圖8中的陰影區域所示。這也驗證了式(22)～(24)的有效性。

圖8 銑削穩定性葉瓣圖Fig.8 Stability lobe diagram

4 結 論

本文基于線性切削力模型，給出了一種螺旋齒銑刀銑削力的一種解析計算表達式。利用該表達式可以有效簡化螺旋齒立銑加工動力學方程的求解或分析過程：

(1) 采用本文所提方法求解銑削動力學方程，不需要對刀具沿軸向離散為微元，因此不存在軸向離散帶來的計算誤差，也因此不需要在求解方程的每一個時間步進行軸向循環計算切削力，從而提高計算精度和效率。采用本文方法求解螺旋齒立銑動力學方程所需計算量與求解直齒銑削動力學方程相當。

(2) 大部分基于時域解的銑削過程穩定性分析需要針對不同主軸轉速和軸向切深求解銑削動力學方程，因此計算非常耗時。半離散法或全離散法雖然不直接采用數值方法求解銑削動力學方程，但是也需要對一個時滯周期內的銑削力進行時域離散近似。因此，本文所提方法可以提高螺旋齒立銑穩定性分析效率。

參 考 文 獻

[1] BUDAK E, ALTINTAS Y.Analytical prediction of chatter stability in milling-Part I: General formulation[J].Journal of Dynamic Systems Measurement and Control-transactions of The Asme, 1998, 120(1): 22-30.

[2] ALTINTAS Y, ENGIN S.Generalized modeling of mechanics and dynamics of milling cutters[J].CIRP Annals-Manufacturing Technology, 2001, 50(1): 25-30.

[3] ENGIN S, ALTINTAS Y.Mechanics and dynamics of general milling cutters.: Part I: helical end mills[J].International Journal of Machine Tools and Manufacture, 2001, 41(15): 2195-2212.

[4] BALACHANDRAN B, ZHAO M X.A mechanics based model for study of dynamics of milling operations[J].Meccanica, 2000, 35(2): 89-109.

[5] ZHAO M X, BALACHANDRAN B.Dynamics and stability of milling process[J].International Journal of Solids & Structures, 2001, 38(10): 2233-2248.

[6] MERDOL S D, ALTINTAS Y.Multi frequency solution of chatter stability for low immersion milling[J].Journal of Manufacturing Science & Engineering, 2004, 126(3): 459-466.

[7] INSPERGER T, MUNOA J, ZATARAIN M A, et al.Unstable islands in the stability chart of milling processes due to the helix angle[J].CIRP 2nd International Conference on High Performance Cutting, 2006: 12-13.

[9] SCHMITZ T L, SMITH K S.Machining dynamics: frequency response to improved productivity [M].Springer US, 2008.

[10] SIMS N D, MANN B, HUYANAN S.Analytical prediction of chatter stability for variable pitch and variable helix milling tools[J].Journal of Sound & Vibration, 2008, 317(3/4/5): 664-686.

[11] DOMBOVARI Z, STEPAN G.The effect of harmonic helix angle variation on milling stability[J].Journal of Manufacturing Science & Engineering, 2011, 134(5): 921-922.

[12] 丁燁.銑削動力學——穩定性分析方法與應用 [D]上海：上海交通大學, 2011.

[13] 劉強, 李忠群.數控銑削加工過程仿真與優化-建模、算法與工程應用 [M].北京: 航空工業出版社, 2011.

[14] 宋戈, 李劍峰, 孫杰.基于銑削力精確建模的工件表面讓刀誤差預測分析[J].機械工程學報, 2013, 49(21): 168-175.

SONG Ge, LI Jianfeng, SUN Jie.Analysis on prediction of surface error based on precision milling cutting force model[J].Journal of Mechanical Engineering, 2013, 49(21): 168-175.

[15] 蔣宇平, 龍新華, 孟光.薄壁結構件銑削加工振動穩定性分析[J].振動與沖擊, 2016, 35(2): 45-50.

JIANG Yuping, LONG Xinhua, MENG Guang.Stability analysis for thin-walled milling processes[J].Journal of Vibration and Shock, 2016, 35(2): 45-50.